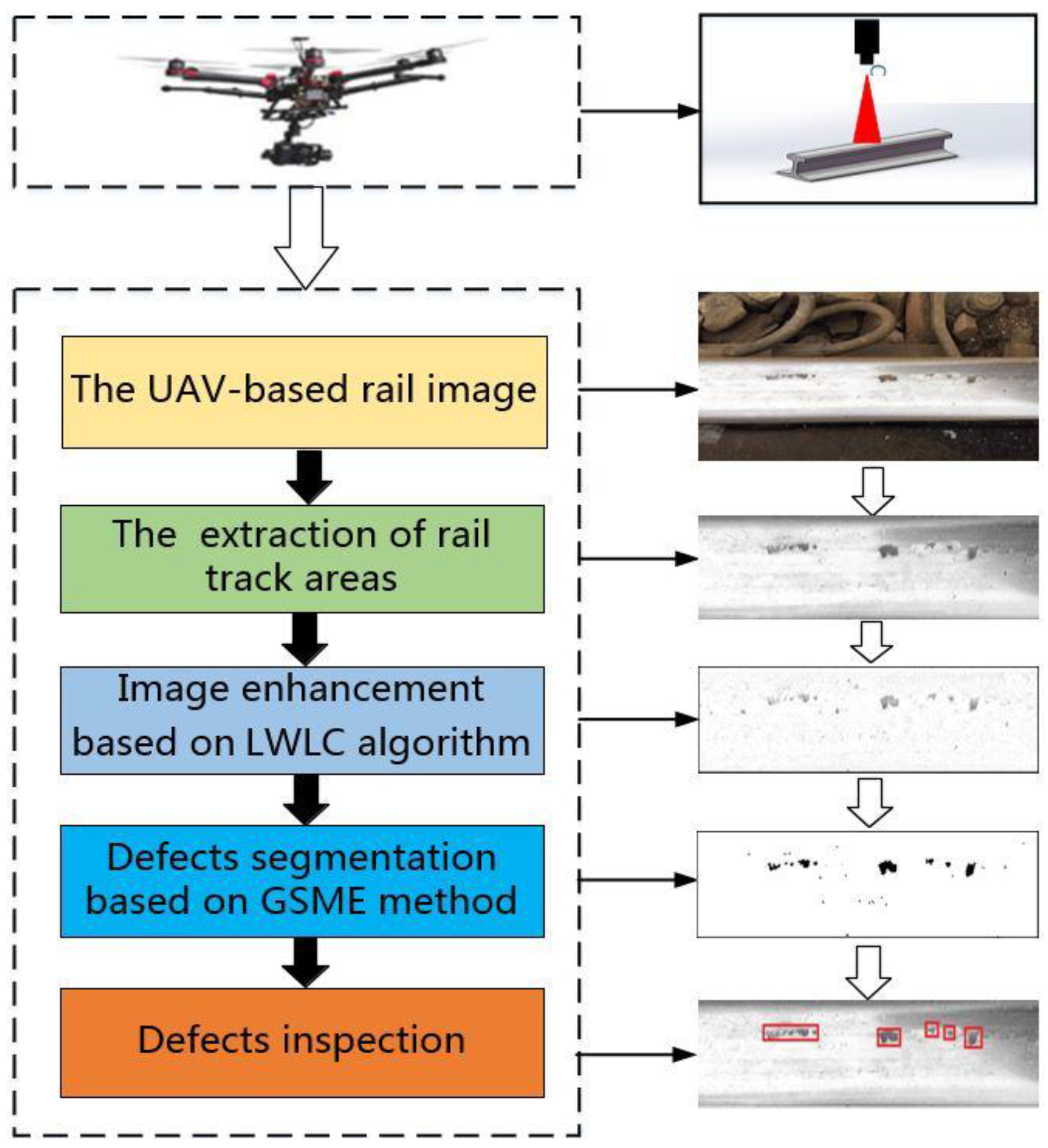
A UAV-Based Visual Inspection Method for Rail Surface Defects
Abstract
:1. Introduction
- Rail position variances in UAV images. Unlike inspection trains, the camera angle of HD camera installed on UAV is sensitive to environment aspects (such as wind and turbulence) and operators. Although the UAV can balance itself by using GPS flight mode, rail positions in images captured by UAV aerial photography are extremely variable. Therefore, the variances of rail positions bring difficulties to rail extraction.
- Non-uniform illumination and noise corruption. Due to partial occlusion of infrastructures around the rail (such as catenary etc.), reflectance properties of rail surface and shake of the UAV and other environmental factors, the brightness and contrast of images are uneven and low. According to [17,31], UAV digital images are likely to be corrupted by noises during the acquisition or transmission. In general, the gray levels of surface defects are lower than that of background (non-defect area) [14], but the order of these values is often broken because of non-uniform illumination and noise corruption, as shown in the Figure 1.
- Few characteristics for defects segmentation. A corrugation initiates and develops easily because of the periodic occurrence of contact vibration [32]. However, it is difficult to inspect discrete defects by the VI method due to the lack of periodicity. Surface defects have low grey-level, that distinguishes them from the dynamic background. Therefore, the grey-level is considered to be the most available feature [14]. Therefore, the existing object recognition methods based on sophisticated texture and shape features are unfeasible, due to the limitation of visual features [15].
2. Methodology
2.1. Rail Track Extraction
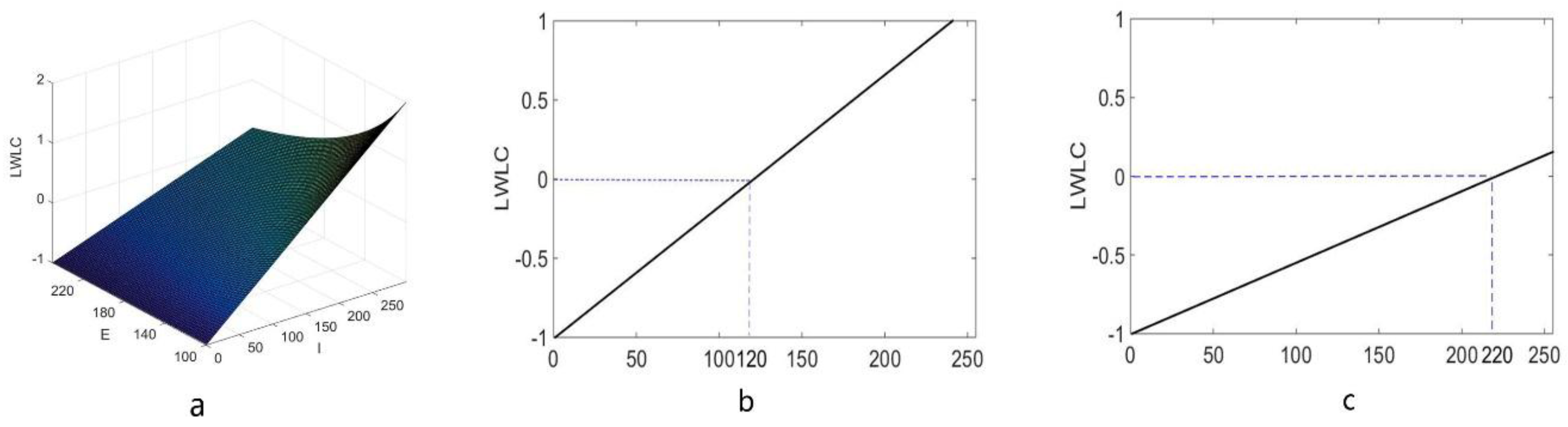
2.2. The Local Weber-Like Contrast Algorithm for Rail Images Enhancement
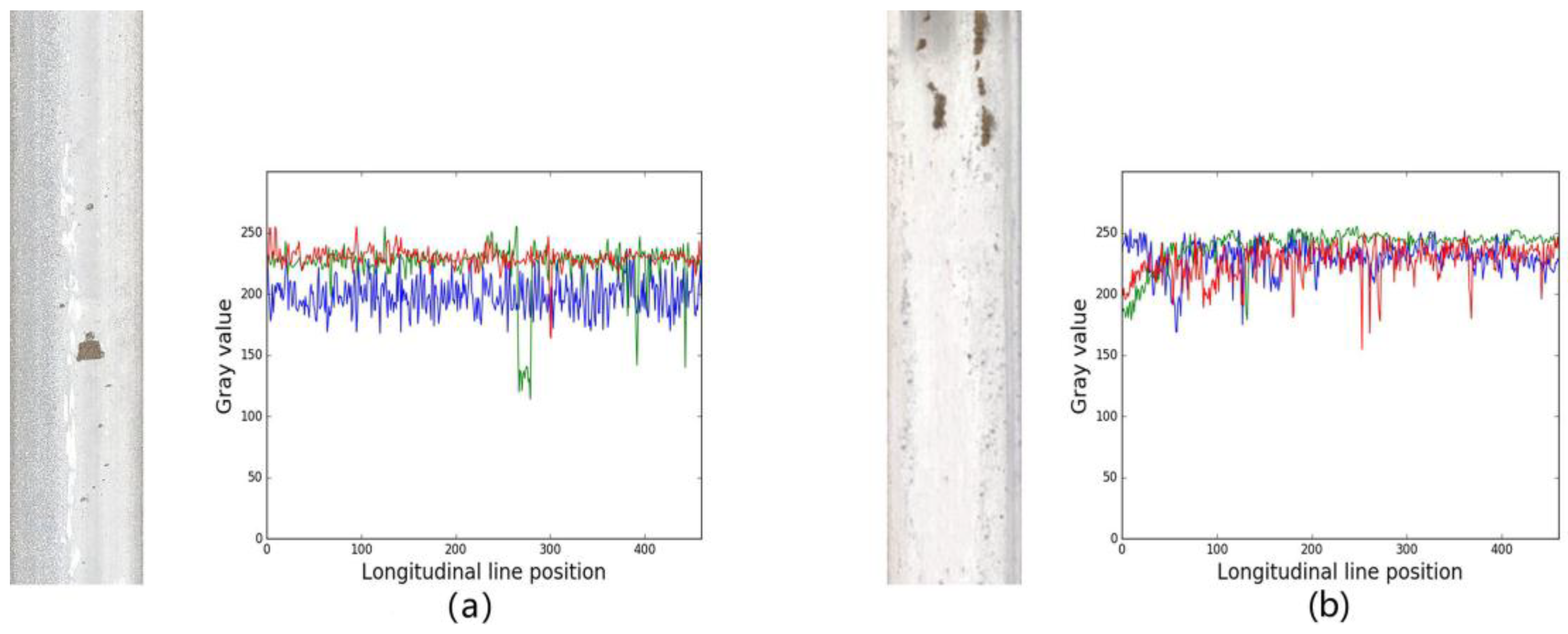
- Lower variation range of gray values in local regions. The reflection property and illumination of each longitudinal line in rail images is stable [14]. In the local line window, the variation range of gray values has small variation, and the most obvious features can be used for image enhancement [15].
- Greater variation range of gray values in global scope. In general, the rail images have a large variation range of gray level in global scope due to uneven natural light and the reflectance properties of rail surfaces. The reflected light in smooth parts of rail surfaces is more than the rough parts [42].
- Confused gray values between defects and background. In general, the gray value of surface defects is lower than that of background, but the order is often broken because of illumination non-uniformity and noise corruption, as shown in the Figure 4.
- Consistent features in the same longitudinal direction. Actually, a rail surface shares consistent features in the longitudinal direction as a train runs on a rail, since the friction for the points in the longitudinal direction between the rail surface and train wheels has an almost identical impact on the rail surface. In a rail image, intensity for the pixel points along longitudinal direction is consistent with relatively gray value changes caused by defect points and noise points [15]. Therefore, the surface discrete defects can be derived by the analysis of the information in longitudinal regions.
- Higher gray mean of each longitudinal line for a track. According to our observation, the gray means along longitudinal lines of a UAV rail image are higher under normal conditions. This is because that UAV are supposed to fly in fine weathers and natural light conditions, and the surface reflectivity of rail tracks in operation is high because of its smoothness, as shown in the Figure 4.
- (i)
- By convolution with an image matrix I and a designed lined window, calculates LWLC value of each pixel in I by Equation (6), so that a LWLC matrix can be acquired.
- (ii)
- Mapping gray-values of the LWLC matrix to [0, 255].
2.3. Defect Segmentation Mehtod Based on Gray Stretch Maximum Entropy
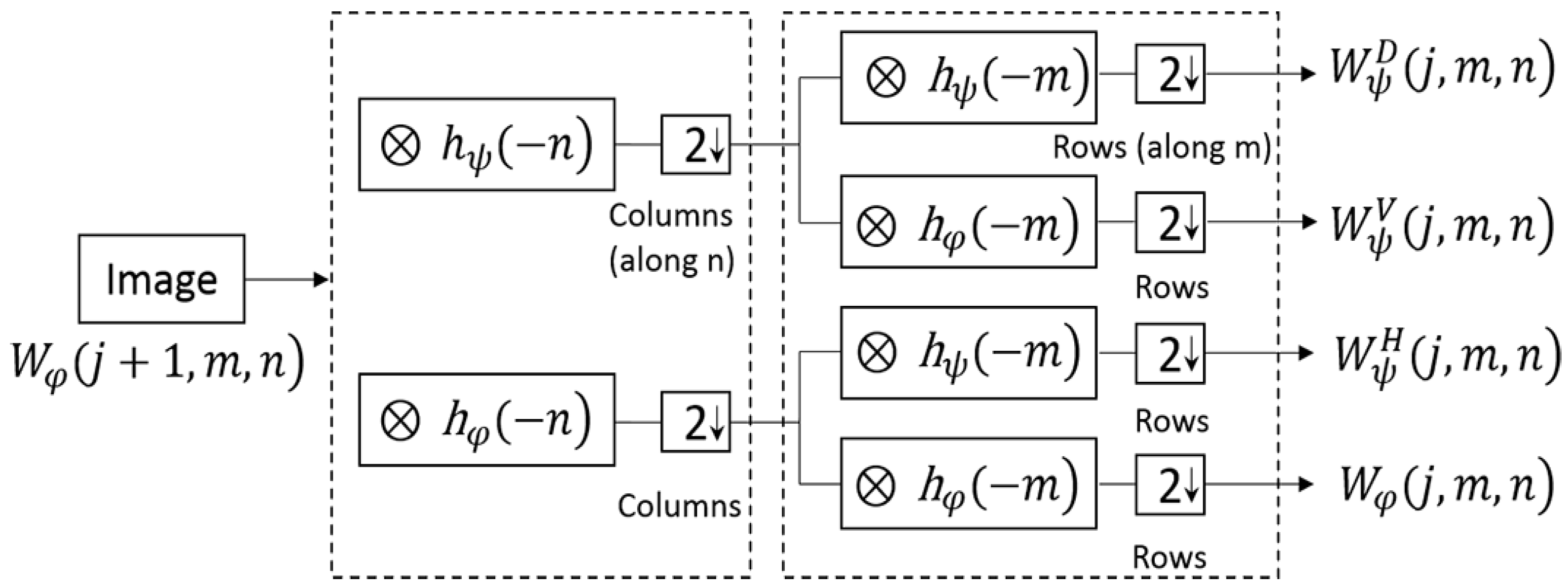
2.3.1. A Brief Introduction for 2-D Discrete Wavelet Transform
2.3.2. The Gray Stretch Maximum Entropy Threshold Method
- (i)
- Based on one-level 2-D DWT algorithm, the rail image is decomposed into four wavelet coefficients that include approximation (low frequency region), horizontal, vertical, and diagonal details.
- (ii)
- For low frequency region (LL region) of image decomposed by wavelet, the ME algorithm is used to obtain a segmentation threshold after reconstructing its coefficient, and then the gray stretch method is used to enhance contrast between background and foreground, as the following equations:where denotes reconstructing image function, a denotes stretch factor and is set to and value between 0.1 and 0.5 in general.
- (iii)
- For the image, its energy is mainly distributed in the low frequency region. In the high frequency area, the proportion of noise energy is large, so this study focuses on de-noising in this area. In Ref [39], Tang et al. use the filter templates of three different directions for de-noising. For example, the line template of horizontal direction is used for de-noising, because the wavelet coefficients contain the high-frequency information in the horizontal direction and low-frequency information in the vertical direction of the image signal. Inspired by the median filtering method employed in wavelet domain, this study used the median filtering template of horizontal line, vertical line, and diagonal line to eliminate noise of three high frequency wavelet coefficients, respectively.
- (iv)
- The rail image can be reconstructed based on discrete wavelet inverse transform algorithm. The formula for reconstruction image is given by:
- (v)
- The ME algorithm is used to select a segmentation threshold after reconstructing the rail image by discrete wavelet inverse transform.
3. Experiment Results
3.1. Experiment Setup
3.1.1. A Brief Introduction of the Equipment for UAV Images Acquisition
3.1.2. Experiment Environment
3.1.3. Defects and Evaluation
3.2. Performance Analysis
3.2.1. Image Enhancement
3.2.2. Defect Segmentation
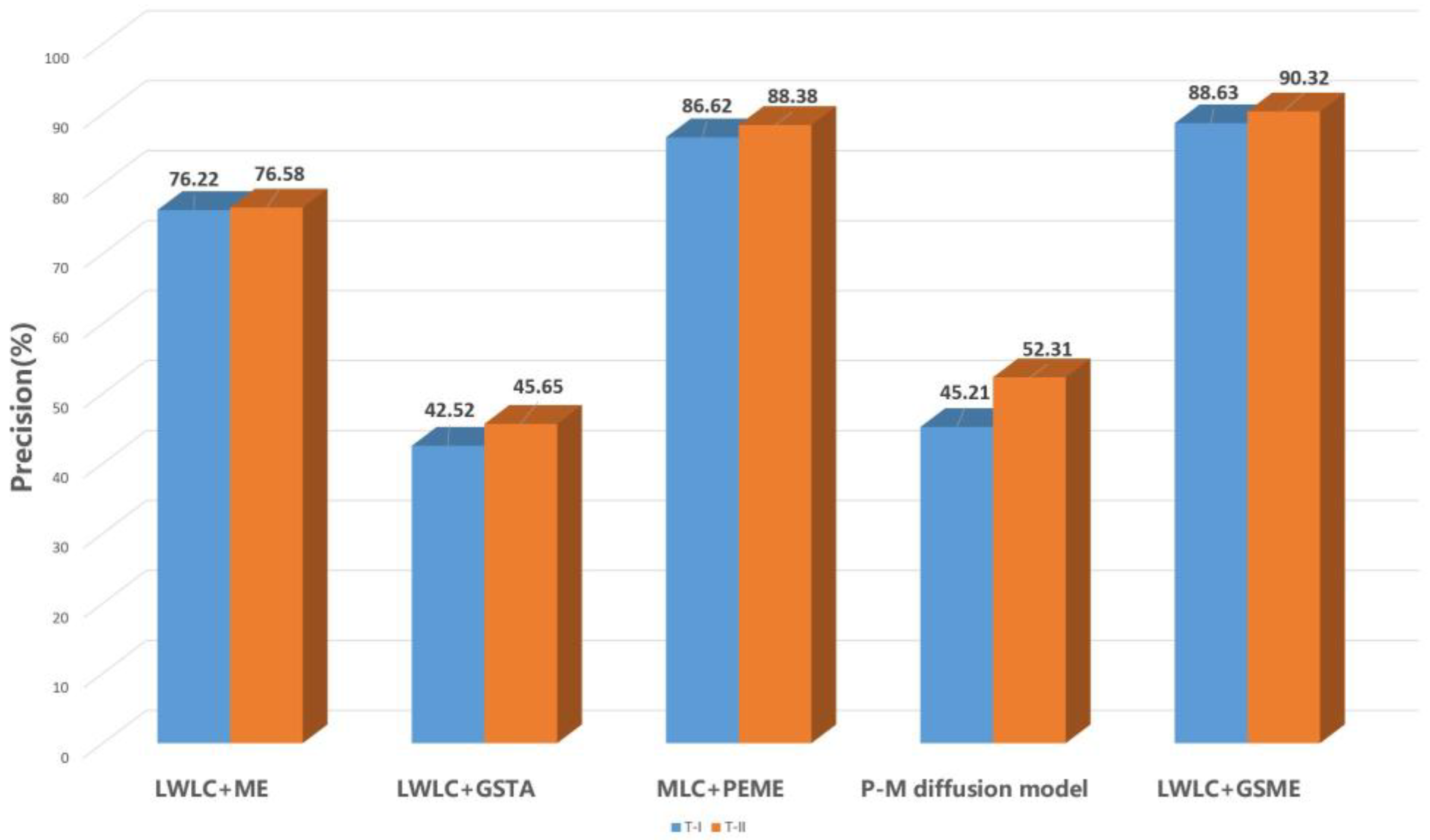
3.2.3. Qualitative Comparison between LWLC+GSME and Related Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Algorithm A1. The Algorithm A1 for track extraction. |
| 1 procedure Algorithm A1 (Cg(n), Wd) 2 for m ← 1, M − Wd + 1 do 3 for n ← m, Wd do /* Wd is the width of the rail track.*/ 4 Cg(n) ← Cg(n) + Cg(n + 1) 5 CumCg(m) ← Cg(n) 6 end for 7 maxCumCg ← −1 8 p_left ← 0 9 for m ← 1, M − Wd + 1 do 10 p_CumCg ← CumCg(m) 11 if p_CumCg > maxCumCg then 12 maxCumCg ← p_CumCg 13 p_left ← m 14 end if 15 end for 16 return p_left /* The most left position of a rail track (p_left)*/ |
| 17 end procedure |

References
- Arivazhagan, S.; Shebiah, R.N.; Magdalene, J.S.; Sushmitha, G. Railway track derailment inspection system using segmentation based fractal texture analysis. ICTACT J. Image Video Process. 2015, 6, 1060–1065. [Google Scholar]
- Cannon, D.; Edel, K.O.; Grassie, S.; Sawley, K. Rail defects: An overview. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 865–886. [Google Scholar] [CrossRef]
- Grassie, S. Rail corrugation: Characteristics, causes, and treatments. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 581–596. [Google Scholar] [CrossRef]
- Edwards, J.R.; Hart, J.M.; Sawadisavi, S.; Resendiz, E.; Barkan, C.; Ahuja, N. Advancements in Railroad Track Inspection Using Machine-Vision Technology. In Proceedings of the AREMA Conference on American Railway and Maintenance of Way Association, Chicago, IL, USA, 2–5 August 2009. [Google Scholar]
- Marino, F.; Distante, A.; Mazzeo, P.L.; Stella, E. A real-time visual inspection system for railway maintenance: Automatic hexagonal-headed bolts detection. IEEE Trans. Syst. Man Cybern. Part. C (Appl. Rev.) 2007, 37, 418–428. [Google Scholar] [CrossRef]
- Tsai, D.-M.; Wu, S.-C.; Chiu, W.-Y. Defect detection in solar modules using ICA basis images. IEEE Trans. Ind. Inform. 2013, 9, 122–131. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, N.; Wang, Y.; Shen, Y. An analysis of the simulated acoustic emission sources with different propagation distances, types and depths for rail defect detection. Appl. Acoust. 2014, 86, 80–88. [Google Scholar] [CrossRef]
- Liu, Z.; Li, W.; Xue, F.; Xiafang, J.; Bu, B.; Yi, Z. Electromagnetic tomography rail defect inspection. IEEE Trans. Magn. 2015, 51, 1–7. [Google Scholar] [CrossRef]
- Hesse, D.; Cawley, P. The Potential of Ultrasonic Surface Waves for Rail Inspection. In Proceedings of the AIP Conference, Golden, CO, USA, 25–30 July 2004; American Institute of Physics: College Park, MD, USA, 2005; Volume 760, pp. 227–234. [Google Scholar]
- Tang, X.-N.; Wang, Y.-N. Visual inspection and classification algorithm of rail surface defect. Comput. Eng. 2013, 9, 25–30. [Google Scholar]
- Resendiz, E.; Hart, J.M.; Ahuja, N. Automated visual inspection of railroad tracks. IEEE Trans. Intell. Transp. Syst. 2013, 14, 751–760. [Google Scholar] [CrossRef]
- Liu, J.; Li, B.; Xiong, Y.; He, B.; Li, L. Integrating the symmetry image and improved sparse representation for railway fastener classification and defect recognition. Math. Probl. Eng. 2015, 2015, 462528. [Google Scholar] [CrossRef]
- Ph Papaelias, M.; Roberts, C.; Davis, C. A review on non-destructive evaluation of rails: State-of-the-art and future development. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2008, 222, 367–384. [Google Scholar] [CrossRef]
- Li, Q.; Ren, S. A real-time visual inspection system for discrete surface defects of rail heads. IEEE Trans. Instrum. Meas. 2012, 61, 2189–2199. [Google Scholar] [CrossRef]
- Gan, J.; Li, Q.; Wang, J.; Yu, H. A hierarchical extractor-based visual rail surface inspection system. IEEE Sensors J. 2017, 17, 7935–7944. [Google Scholar] [CrossRef]
- He, Z.; Wang, Y.; Yin, F.; Liu, J. Surface defect detection for high-speed rails using an inverse pm diffusion model. Sens. Rev. 2016, 36, 86–97. [Google Scholar] [CrossRef]
- Sieberth, T.; Wackrow, R.; Chandler, J.H. Automatic detection of blurred images in UAV image sets. ISPRS J. Photogramm. Remote Sens. 2016, 122, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Siebert, S.; Teizer, J. Mobile 3d mapping for surveying earthwork projects using an unmanned aerial vehicle (UAV) system. Autom. Constr. 2014, 41, 1–14. [Google Scholar] [CrossRef]
- Pérez-Ortiz, M.; Peña, J.M.; Gutiérrez, P.A.; Torres-Sánchez, J.; Hervás-Martínez, C.; López-Granados, F. Selecting patterns and features for between-and within-crop-row weed mapping using UAV-imagery. Expert Syst. Appl. 2016, 47, 85–94. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z. Automatic detection of wind turbine blade surface cracks based on UAV-taken images. IEEE Trans. Ind. Electron. 2017, 64, 7293–7303. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Y.; Wu, H.; Dong, R. A safe flight approach of the UAV in the electrical line inspection. Int. J. Emerg. Electr. Power Syst. 2015, 16, 503–515. [Google Scholar] [CrossRef]
- Kaamin, M.; Idris, N.A.; Bukari, S.M.; Ali, Z.; Samion, N.; Ahmad, M.A. Visual Inspection of Historical Buildings Using Micro UAV. In Proceedings of the MATEC Web of Conferences, Qingdao, China, 25–27 August 2017; EDP Sciences: Paris, France, 2017; Volume 103, p. 07003. [Google Scholar]
- Yuan, C.; Liu, Z.; Zhang, Y. UAV-Based Forest Fire Detection and Tracking Using Image Processing Techniques. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 639–643. [Google Scholar]
- Rau, J.; Hsiao, K.; Jhan, J.; Wang, S.; Fang, W.; Wang, J. Bridge crack detection using multi-rotary UAV and object-base image analysis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 311. [Google Scholar] [CrossRef]
- Arenella, A.; Greco, A.; Saggese, A.; Vento, M. In Real Time Fault Detection in Photovoltaic Cells by Cameras on Drones. In Proceedings of the 14th International Conference on Image Analysis and Recognition, Montreal, QC, Canada, 5–7 July 2017; Springer: New York, NY, USA, 2017; pp. 617–625. [Google Scholar]
- Xiao, Q.; Zhang, Q.; Wu, X.; Han, X.; Li, R. Learning Binary Code Features for UAV Target Tracking. In Proceedings of the 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 65–68. [Google Scholar]
- Baykara, H.C.; Bıyık, E.; Gül, G.; Onural, D.; Öztürk, A.S. Real-Time Detection, Tracking and Classification of Multiple Moving Objects in UAV Videos. In Proceedings of the 2017 IEEE 29th International Conference on Tools with Artificial Intelligence (ICTAI), Boston, MA, USA, 6–8 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 945–950. [Google Scholar]
- Radovic, M.; Adarkwa, O.; Wang, Q. Object recognition in aerial images using convolutional neural networks. J. Imaging 2017, 3, 21. [Google Scholar] [CrossRef]
- Liang, L.; He, W.-P.; Lei, L.; Zhang, W.; Wang, H.-X. Survey on enhancement methods for non-uniform illumination image. Appl. Res. Comput. 2010, 5, 008. [Google Scholar]
- Li, Q.; Ren, S. A visual detection system for rail surface defects. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2012, 42, 1531–1542. [Google Scholar] [CrossRef]
- Chen, X.; Xu, J.-P. A denoising algorithm of image for UAV based on wavelet transform and mean-value filtering. Fire Control Command. Control 2011, 8, 049. [Google Scholar]
- Jin, X.; Wen, Z.; Wang, K. Effect of track irregularities on initiation and evolution of rail corrugation. J. Sound Vib. 2005, 285, 121–148. [Google Scholar] [CrossRef]
- Fechner, G. Über ein wichtiges psychophysiches grundgesetz und dessen beziehung zur schäzung der sterngrössen. Abk. K. Ges. Wissensch. Math.-Phys. K 1858, 1, 4. [Google Scholar]
- Shen, J. On the foundations of vision modeling: I. Weber’s law and Weberized TV restoration. Phys. D Nonlinear Phenom. 2003, 175, 241–251. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/Contrast_(vision) (accessed on 1 May 2018).
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Kapur, J.N.; Sahoo, P.K.; Wong, A.K. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Liu, L.; Yang, N.; Lan, J.; Li, J. Image segmentation based on gray stretch and threshold algorithm. Opt.-Int. J. Light Electron. Opt. 2015, 126, 626–629. [Google Scholar] [CrossRef]
- Tang, S.-W.; Lin, J. Image denoising with combination of wavelet transform and median filtering. J. Harbin Inst. Technol. 2002, 24, 1334–1336. [Google Scholar]
- Rakheja, P.; Vig, R. Image denoising using combination of median filtering and wavelet transform. Int. J. Comput. Appl. 2016, 141, 31–35. [Google Scholar] [CrossRef]
- Jin, B.; Niu, H.; Hou, T. Study of straight line rail image edge detection based on improved hough. Video Eng. 2015, 39, 17–19. [Google Scholar]
- Li, Q.; Tan, Y.; Huayan, Z.; Ren, S.; Dai, P.; Li, W. A Visual Inspection System for Rail Corrugation Based on Local Frequency Features. In Proceedings of the 2016 IEEE 14th International Conference on Dependable, Autonomic and Secure Computing, 14th International Conference on Pervasive Intelligence and Computing, 2nd International Conference on Big Data Intelligence and Computing and Cyber Science and Technology Congress (DASC/PiCom/DataCom/CyberSciTech), Auckland, New Zealand, 8–12 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 18–23. [Google Scholar]
- Whittle, P. The psychophysics of contrast brightness. In Lightness, Brightness, and Transparency; Gilchrist, A.L., Ed.; Lawrence Erlbaum Associates, Inc.: Hillsdale, NJ, USA, 1994; pp. 35–110. [Google Scholar]
- Arend, L.E.; Spehar, B. Lightness, brightness, and brightness contrast: 1. Illuminance variation. Percept. Psychophys. 1993, 54, 446–456. [Google Scholar] [CrossRef] [PubMed]
- Agaian, S.S. Visual Morphology. Proc. SPIE 1999, 3646, 139–150. [Google Scholar]
- Rafael, C.; Gonzalez, R.E.W. Digital Image Processing, 3rd ed.; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Pun, T. A new method for grey-level picture thresholding using the entropy of the histogram. Signal. Process. 1980, 2, 223–237. [Google Scholar] [CrossRef]
- Pun, T. Entropic thresholding, a new approach. Comput. Graph. Image Process. 1981, 16, 210–239. [Google Scholar] [CrossRef] [Green Version]
- Xu, W. Study on Defect Recognition for Rail Surface Based on Machine Vision. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 1 March 2015. [Google Scholar]








| Defects Type | T-I Defect | T-II Defect |
|---|---|---|
| Area () | 25 mm2 < ≤ 255 mm2 | 255 mm2 < |
| Defects Inspection Model | LWLC+ME | LWLC+GSTA | MLC+PEME | LWLC+GSME |
|---|---|---|---|---|
| Original images (A1) | 228 | 140 | 226 | 189 |
| Original images (A2) | 213 | 120 | 225 | 170 |
| Original images (A3) | 188 | 82 | 206 | 161 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Qin, Y.; Wang, Z.; Jia, L. A UAV-Based Visual Inspection Method for Rail Surface Defects. Appl. Sci. 2018, 8, 1028. https://doi.org/10.3390/app8071028
Wu Y, Qin Y, Wang Z, Jia L. A UAV-Based Visual Inspection Method for Rail Surface Defects. Applied Sciences. 2018; 8(7):1028. https://doi.org/10.3390/app8071028
Chicago/Turabian StyleWu, Yunpeng, Yong Qin, Zhipeng Wang, and Limin Jia. 2018. "A UAV-Based Visual Inspection Method for Rail Surface Defects" Applied Sciences 8, no. 7: 1028. https://doi.org/10.3390/app8071028







