Collusion Attack Resilient 3D Mesh Watermarking Based on Anti-Collusion Fingerprint Code
Abstract
1. Introduction
2. Backgrounds
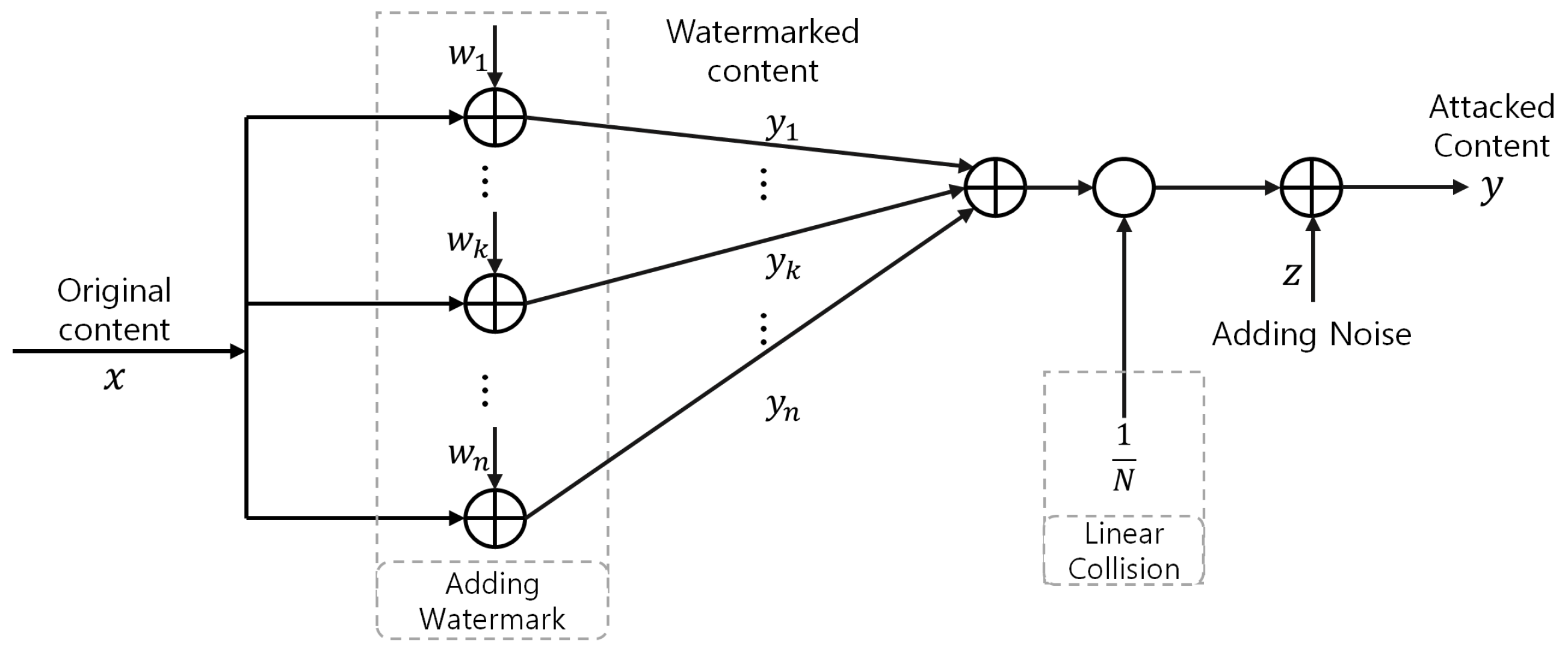
2.1. Model for Collusion Attack
2.2. Related Work
3. Proposed Method
3.1. Watermark Embedding Algorithm
3.2. Watermark Extraction
3.2.1. Detection of the Embedded Watermark
3.2.2. Colluder Accusation
3.3. Detector Response Modeling and Error Minimization
3.4. Extended Mesh Fingerprinting Scheme Using Tardos’s Code
3.4.1. Tardos’s Fingerprint Code
3.4.2. Extended Mesh Fingerprinting Scheme Using Tardos’s Code
4. Experimental Results
4.1. Robustness Test for Collusion Attack
4.2. Robustness Test for Combination of Noise Addition and Collusion Attack
4.3. Experimental Results of Tardos’s Code-Based Scheme
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, K.; Lavoue, G.; Denis, F.; Baskurt, A. A Comprehensive Survey on Three-Dimensional Mesh Watermarking. IEEE Trans. Multimed. 2008, 10, 1513–1527. [Google Scholar] [CrossRef]
- Hou, J.U.; Park, J.S.; Kim, D.G.; Nam, S.H.; Lee, H.K. Robust video watermarking for MPEG compression and DA-AD conversion. In Proceedings of the 1st International Workshop on Information Hiding and Its Criteria for Evaluation, Kyoto, Japan, 3 June 2014; pp. 2–8. [Google Scholar]
- Asikuzzaman, M.; Pickering, M.R. An overview of digital video watermarking. IEEE Trans. Circuits Syst. Video Technol. 2017. [Google Scholar] [CrossRef]
- Boneh, D.; Shaw, J. Collusion-secure fingerprinting for digital data. IEEE Trans. Inf. Theory 1998, 44, 1897–1905. [Google Scholar] [CrossRef]
- Celik, M.U.; Sharma, G.; Tekalp, A.M. Collusion-resilient fingerprinting using random prewarping. In Proceedings of the 2003 International Conference on Image Processing, Barcelona, Spain, 14–17 September 2003; Volume 1, p. 509. [Google Scholar]
- Uccheddu, F.; Kuo, C.C.J.; Barni, M. Anticollusion watermarking of 3D meshes by prewarping. In Proceedings of the SPIE International Society for Optics and Photonics, San Jose, CA, USA, 18 March 2008; p. 68190S. [Google Scholar]
- Stinson, D.R.; Wei, R. Combinatorial properties and constructions of traceability schemes and frameproof codes. SIAM J. Discrete Math. 1998, 11, 41–53. [Google Scholar] [CrossRef]
- Trappe, W.; Wu, M.; Wang, Z.; Liu, K. Anti-collusion fingerprinting for multimedia. IEEE Trans. Sign. Process. 2003, 51, 1069–1087. [Google Scholar] [CrossRef]
- InKoo, K.; Sinha, K.; Lee, H.K. New digital fingerprint code construction scheme using group-divisible design. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2006, 89, 3732–3735. [Google Scholar]
- Zhu, X.; Chen, C.W. A collusion resilient key management scheme for multi-dimensional scalable media access control. In Proceedings of the 18th IEEE International Conference on Image Processing (ICIP), Brussels, Belgium, 11–14 September 2011; pp. 2769–2772. [Google Scholar] [CrossRef]
- Ohbuchi, R.; Takahashi, S.; Miyazawa, T.; Mukaiyama, A. Watermarking 3d polygonal meshes in the mesh spectral domain. In Proceedings of the Graphics Interface, Ottawa, ON, Canada, 7–9 June 2001; Volume 2001, pp. 9–17. [Google Scholar]
- Cho, J.W.; Prost, R.; Jung, H.Y. An Oblivious Watermarking for 3-D Polygonal Meshes Using Distribution of Vertex Norms. IEEE Trans. Sign. Proc. 2007, 55, 142–155. [Google Scholar] [CrossRef]
- Hou, J.U.; Kim, D.G.; Choi, S.; Lee, H.K. 3D Print-Scan Resilient Watermarking Using a Histogram-Based Circular Shift Coding Structure. In Proceedings of the 3rd ACM Workshop on Information Hiding and Multimedia Security, Portland, OR, USA, 17–19 June 2015; ACM: New York, NY, USA, 2015; pp. 115–121. [Google Scholar]
- Itier, V.; Puech, W.; Bors, A. Cryptanalysis aspects in 3-D watermarking. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 4772–4776. [Google Scholar]
- Jong-Uk, H.; In-Jae, Y.; Hyun-Ji, S.; Lee, H.K. Robust 3D Mesh Watermarking Scheme for an Anti-Collusion Fingerprint Code. In Proceedings of the 18th World Conference on Information Security Applications, Daejeon, Korea, 24–26 August 2017; Volume 1, pp. 74–83. [Google Scholar]
- Bollobás, B. Modern Graph Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998; Volume 184. [Google Scholar]
- Tardos, G. Optimal probabilistic fingerprint codes. J. ACM 2008, 55, 10. [Google Scholar] [CrossRef]
- Kang, I.K.; Lee, C.H.; Lee, H.Y.; Kim, J.T.; Lee, H.K. Averaging attack resilient video fingerprinting. In Proceedings of the 2005 IEEE International Symposium on Circuits and Systems (ISCAS), Kobe, Japan, 23–26 May 2005; pp. 5529–5532. [Google Scholar]
- Maity, S.P.; Maity, S.; Sil, J.; Delpha, C. Collusion resilient spread spectrum watermarking in M-band wavelets using GA-fuzzy hybridization. J. Syst. Softw. 2013, 86, 47–59. [Google Scholar] [CrossRef]
- Kuribayashi, M. Simplified MAP detector for binary fingerprinting code embedded by spread spectrum watermarking scheme. IEEE Trans. Inf. Forensics Secur. 2014, 9, 610–623. [Google Scholar] [CrossRef]
- Hou, J.U.; Kim, D.G.; Lee, H.K. Blind 3D Mesh Watermarking for 3D Printed Model by Analyzing Layering Artifact. IEEE Trans. Inf. Forensics Secur. 2017, 12, 2712–2725. [Google Scholar] [CrossRef]
- Jang, H.U.; Choi, H.Y.; Son, J.; Kim, D.; Hou, J.U.; Choi, S.; Lee, H.K. Cropping-resilient 3D mesh watermarking based on consistent segmentation and mesh steganalysis. Multimed. Tools Appl. 2018, 77, 5685–5712. [Google Scholar] [CrossRef]
- Wang, K.; Lavoué, G.; Denis, F.; Baskurt, A. Technical Section: Robust and Blind Mesh Watermarking Based on Volume Moments. Comput. Graph. 2011, 35, 1–19. [Google Scholar] [CrossRef]
- Alface, P.R.; Macq, B.; Cayre, F. Blind and robust watermarking of 3D models: How to withstand the cropping attack? In Proceedings of the 2007 IEEE International Conference on Image Processing, San Antonio, TX, USA, 16 September–19 October 2007; Volume 5, p. 465. [Google Scholar]
- Karni, Z.; Gotsman, C. Spectral compression of mesh geometry. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques; ACM Press/Addison-Wesley Publishing Co.: New York, NY, USA, 2000; pp. 279–286. [Google Scholar]
- Clatworthy, W.H.; Cameron, J.M.; Speckman, J.A. Tables of Two-Associate-Class Partially Balanced Designs; US Government Printing Office: Washington, DC, USA, 1973; Volume 63.
- Wang, K.; Lavoué, G.; Denis, F.; Baskurt, A.; He, X. A benchmark for 3D mesh watermarking. In Proceedings of the IEEE International Conference on Shape Modeling and Applications, Aix-en-Provence, France, 21–23 June 2010; pp. 231–235. [Google Scholar]
- Peyré, G. The Numerical Tours of Signal Processing—Advanced Computational Signal and Image Processing. IEEE Comput. Sci. Eng. 2011, 13, 94–97. [Google Scholar] [CrossRef]
- Cignoni, P.; Rocchini, C.; Scopigno, R. Metro: Measuring Error on Simplified Surfaces; Technical Report; Centre National de la Recherche Scientifique: Paris, France, 1996. [Google Scholar]








© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, J.-U.; Yu, I.-J.; Lee, H.-K. Collusion Attack Resilient 3D Mesh Watermarking Based on Anti-Collusion Fingerprint Code. Appl. Sci. 2018, 8, 1040. https://doi.org/10.3390/app8071040
Hou J-U, Yu I-J, Lee H-K. Collusion Attack Resilient 3D Mesh Watermarking Based on Anti-Collusion Fingerprint Code. Applied Sciences. 2018; 8(7):1040. https://doi.org/10.3390/app8071040
Chicago/Turabian StyleHou, Jong-Uk, In-Jae Yu, and Heung-Kyu Lee. 2018. "Collusion Attack Resilient 3D Mesh Watermarking Based on Anti-Collusion Fingerprint Code" Applied Sciences 8, no. 7: 1040. https://doi.org/10.3390/app8071040
APA StyleHou, J.-U., Yu, I.-J., & Lee, H.-K. (2018). Collusion Attack Resilient 3D Mesh Watermarking Based on Anti-Collusion Fingerprint Code. Applied Sciences, 8(7), 1040. https://doi.org/10.3390/app8071040






