Aerodynamic Performance of Wind Turbine Airfoil DU 91-W2-250 under Dynamic Stall
Abstract
:1. Introduction
2. Method
2.1. Numerical Method
2.2. Oscillation of the Airfoil
- is the angle of attack at flow time t,
- is the mean angle of attack,
- is the pitch oscillation amplitude,
- is the oscillation angular frequency.
2.3. Grid Sensitivity
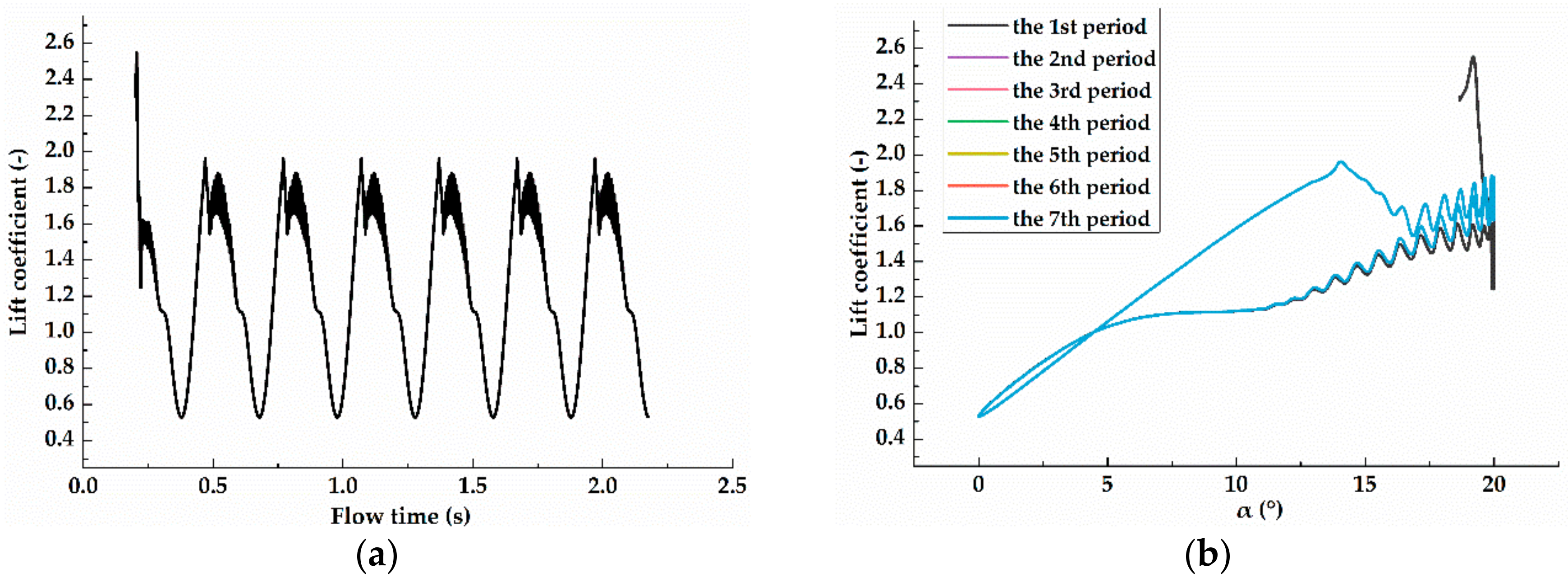
2.4. Time Step and Periodic Repeatability
2.5. Comparison of the Static Result with Experiment and Vortex Panel Method
3. Results and Discussions
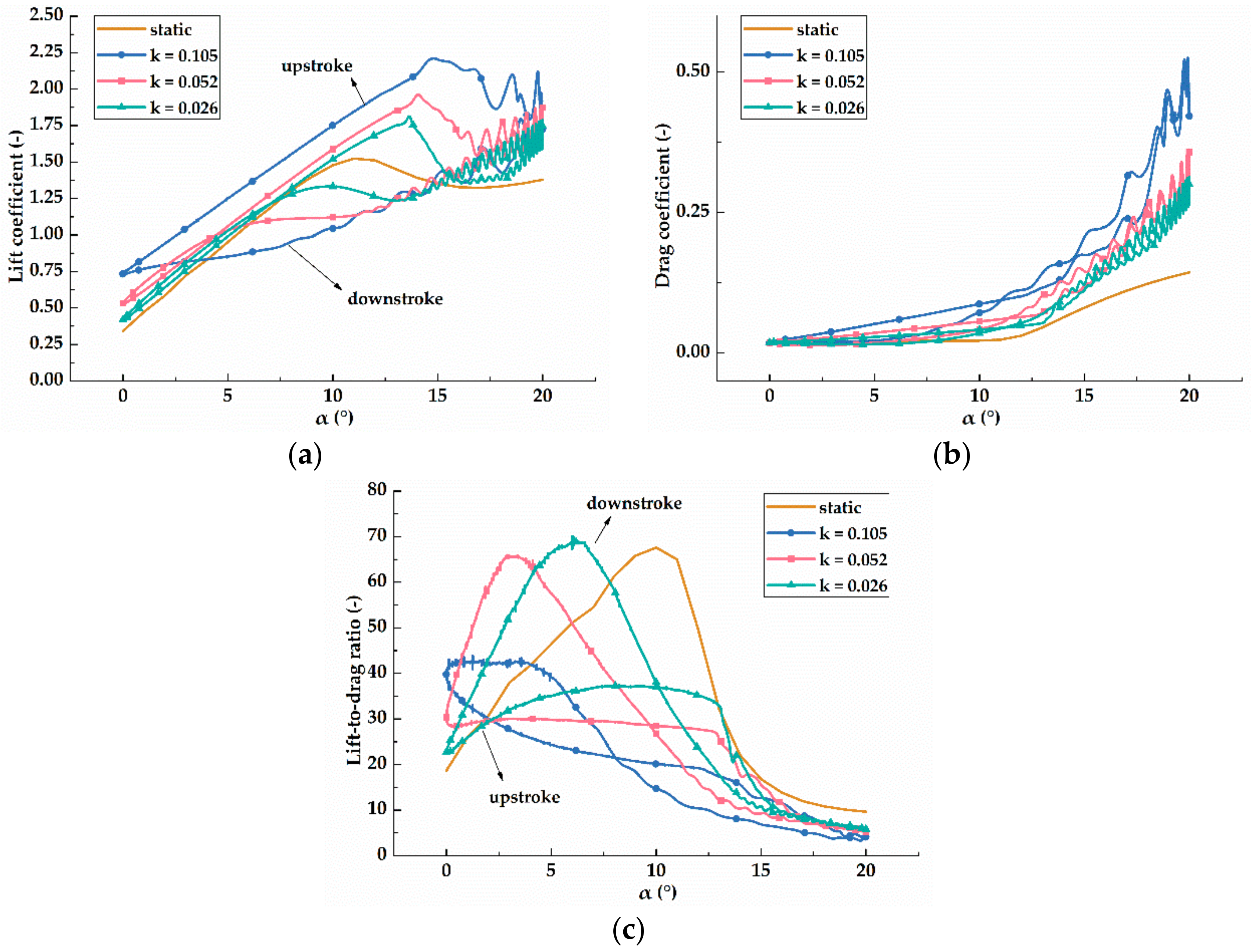
3.1. Effects of Reduced Frequency on Aerodynamic Coefficients
3.2. Flow Development and Separation Points on the Suction Surface of the Airfoil
3.3. Frequency Spectrum Analysis of the Pressure Coefficient
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature/Abbreviations
| c | chord of airfoil (m) |
| skin friction coefficient, | |
| lift coefficient, | |
| pressure coefficient, | |
| f | pitch oscillation frequency (Hz) |
| frequency of shedding vortices | |
| k | reduced frequency, |
| L | lift force (N) |
| p | pressure at one point (Pa) |
| t | time (s) |
| T | time period (s) |
| characteristic time (s) | |
| velocity (m/s) | |
| free-stream velocity (m/s) | |
| height of the first grid in the boundary layer of the airfoil (m) | |
| dimensionless wall distance | |
| angle of attack (deg) | |
| angle of attack at flow time t (deg) | |
| mean angle of attack (deg) | |
| amplitude of angle of attack (deg) | |
| time step (s) | |
| density (kg/) | |
| wall shear stress in the x direction (Pa) | |
| angular frequency (rad/s) | |
| 2D | two-dimensional |
| CFD | computational fluid dynamics |
| CFL | Courant, Friedrichs and Levy criterion |
| DES | detached eddy simulation |
| DNS | direct numerical simulation |
| dt1, dt2… | time step size 1, time step size 2… |
| DU | Delft University of Technology |
| FFT | fast fourier transform |
| G1, G2… | gird case 1, grid case 2… |
| LEV | leading edge vortex |
| N-S | Navier-Stokes |
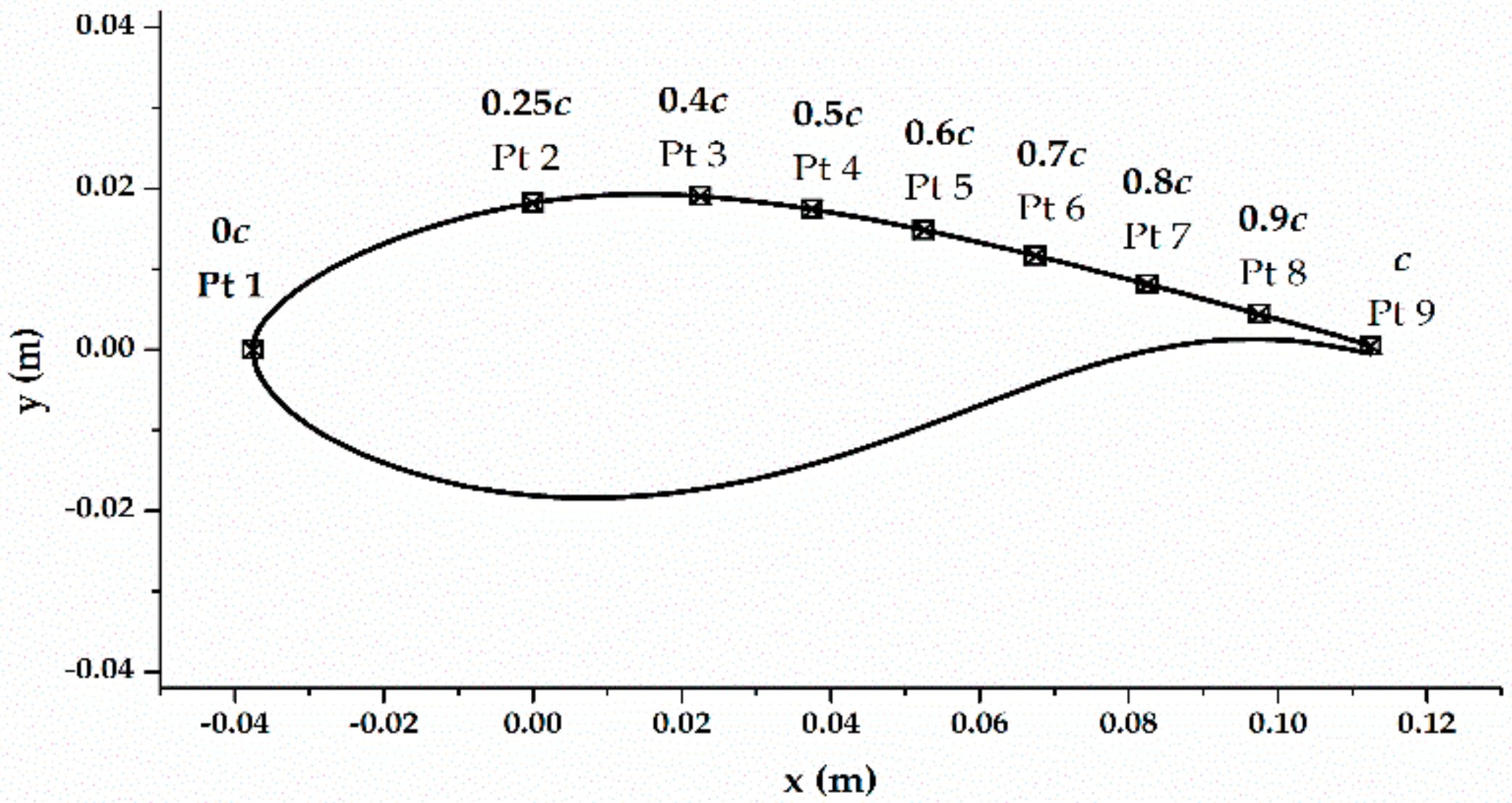
| Pt1, Pt2… | point1, point2… |
| RANS | Reynolds-averaged Navier–Stokes |
| RNG | renormalization-group |
| SST | shear stress transport |
| UDF | user-defined function |
| URANS | unsteady Reynolds-averaged Navier–Stokes |
References
- Leishman, J.G. Principles of Helicopter Aerodynamics; Cambridge University Press: Cambridge, UK, 2006; p. 78. ISBN 9781107013353. [Google Scholar]
- Holierhoek, J.; De Vaal, J.; Van Zuijlen, A.; Bijl, H. Comparing different dynamic stall models. Wind Energy 2013, 16, 139–158. [Google Scholar] [CrossRef]
- Choudhry, A.; Leknys, R.; Arjomandi, M.; Kelso, R. An insight into the dynamic stall lift characteristics. Exp. Therm. Fluid Sci. 2014, 58, 188–208. [Google Scholar] [CrossRef]
- Xiong, L.; Xianmin, Z.; Gangqiang, L.; Yan, C.; Zhiquan, Y. Dynamic response analysis of the rotating blade of horizontal axis wind turbine. Wind Eng. 2010, 34, 543–559. [Google Scholar] [CrossRef]
- Ham, N.D. Aerodynamic loading on a two-dimensional airfoil during dynamic stall. AIAA J. 1968, 6, 1927–1934. [Google Scholar] [CrossRef]
- Galvanetto, U.; Peiró, J.; Chantharasenawong, C. An assessment of some effects of the nonsmoothness of the leishman–beddoes dynamic stall model on the nonlinear dynamics of a typical aerofoil section. J. Fluids Struct. 2008, 24, 151–163. [Google Scholar] [CrossRef]
- Tarzanin, F. Prediction of control loads due to blade stall. J. Am. Helicopter Soc. 1972, 17, 33–46. [Google Scholar] [CrossRef]
- Tran, C.; Petot, D. Semi-Empirical Model for the Dynamic Stall of Airfoils in View of the Application to the Calculation of Responses of a Helicopter Blade in Forward Flight. Vertica 1981, 5, 35–53. [Google Scholar]
- Leishman, J.G.; Beddoes, T. A semi-empirical model for dynamic stall. J. Am. Helicopter Soc. 1989, 34, 3–17. [Google Scholar] [CrossRef]
- Larsen, J.W.; Nielsen, S.R.; Krenk, S. Dynamic stall model for wind turbine airfoils. J. Fluids Struct. 2007, 23, 959–982. [Google Scholar] [CrossRef]
- Hansen, M.H.; Gaunaa, M.; Madsen, H.A. A Beddoes–Leishman Type Dynamic Stall Model in State-Space and Indicial Formulation; Technical University of Denmark: Lyngby, Denmark, 2004; ISBN 8755030890. [Google Scholar]
- Gupta, S.; Leishman, J.G. Dynamic stall modelling of the s809 aerofoil and comparison with experiments. Wind Energy 2010, 9, 521–547. [Google Scholar] [CrossRef]
- Sheng, W.; Galbraith, R.A.M.; Coton, F.N. A modified dynamic stall model for low mach numbers. J. Sol. Energy Eng. 2008, 130, 653. [Google Scholar] [CrossRef]
- Martinat, G.; Braza, M.; Harran, G.; Sevrain, A.; Tzabiras, G.; Hoarau, Y.; Favier, D. Dynamic Stall of a Pitching and Horizontally Oscillating Airfoil; Springer: Berlin, Germany, 2009; pp. 395–403. [Google Scholar]
- Wang, S.; Ingham, D.B.; Ma, L.; Pourkashanian, M.; Tao, Z. Numerical investigations on dynamic stall of low reynolds number flow around oscillating airfoils. Comput. Fluids 2010, 39, 1529–1541. [Google Scholar] [CrossRef]
- Akbari, M.H.; Price, S.J. Simulation of dynamic stall for a naca 0012 airfoil using a vortex method. J. Fluids Struct. 2003, 17, 855–874. [Google Scholar] [CrossRef]
- Gharali, K.; Johnson, D.A. Dynamic stall simulation of a pitching airfoil under unsteady freestream velocity. J. Fluids Struct. 2013, 42, 228–244. [Google Scholar] [CrossRef]
- Kim, Y.; Xie, Z.T. Modelling the effect of freestream turbulence on dynamic stall of wind turbine blades. Comput. Fluids 2016, 129, 53–66. [Google Scholar] [CrossRef] [Green Version]
- Gandhi, A.; Merrill, B.; Peet, Y.T. Effect of Reduced Frequency on Dynamic Stall of a Pitching Airfoil in a Turbulent Wake. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0720. [Google Scholar] [CrossRef]
- Martin, J.; Empey, R.; McCroskey, W.; Caradonna, F. An experimental analysis of dynamic stall on an oscillating airfoil. J. Am. Helicopter Soc. 1974, 19, 26–32. [Google Scholar] [CrossRef]
- Mccroskey, W.J. Unsteady airfoils. Annu. Rev. Fluid Mech. 2003, 14, 285–311. [Google Scholar] [CrossRef]
- McCroskey, W.J. The Phenomenon of Dynamic Stall; NASA Ames Research Center: Mountain View, CA, USA, 1981. [Google Scholar] [CrossRef]
- Wernert, P.; Geissler, W.; Raffel, M.; Kompenhans, J. Experimental and numerical investigations of dynamic stall on a pitching airfoil. AIAA J. 1996, 34, 982–989. [Google Scholar] [CrossRef]
- Aramendia, I.; Fernandez-Gamiz, U.; Ramos-Hernanz, J.A.; Sancho, J.; Lopez-Guede, J.M.; Zulueta, E. Flow control devices for wind turbines. In Energy Harvesting and Energy Efficiency; Springer: Berlin, Germany, 2017; pp. 629–655. [Google Scholar]
- Johnson, S.J.; Baker, J.P.; Van Dam, C.P.; Berg, D. An overview of active load control techniques for wind turbines with an emphasis on microtabs. Wind Energy 2010, 13, 239–253. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Yang, K.; Xue, D. Effects of vortex generators on aerodynamic performance of thick wind turbine airfoils. J. Wind Eng. Ind. Aerodyn. 2016, 156, 84–92. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, L.; Jianzhong, X.U. Simulation of aerodynamic performance affected by vortex generators on blunt trailing-edge airfoils. Sci. China Technol. Sci. 2010, 53, 1–7. [Google Scholar] [CrossRef]
- Tsai, K.-C.; Pan, C.-T.; Cooperman, A.M.; Johnson, S.J.; Van Dam, C. An innovative design of a microtab deployment mechanism for active aerodynamic load control. Energies 2015, 8, 5885–5897. [Google Scholar] [CrossRef]
- Fernandez-Gamiz, U.; Zulueta, E.; Boyano, A.; Ramos-Hernanz, J.A.; Lopez-Guede, J.M. Microtab design and implementation on a 5 mw wind turbine. Appl. Sci. 2017, 7, 536. [Google Scholar] [CrossRef]
- Barlas, T.K.; Van Kuik, G. Review of state of the art in smart rotor control research for wind turbines. Prog. Aerosp. Sci. 2010, 46, 1–27. [Google Scholar] [CrossRef]
- Fernandez-Gamiz, U.; Zulueta, E.; Boyano, A.; Ansoategui, I.; Uriarte, I. Five megawatt wind turbine power output improvements by passive flow control devices. Energies 2017, 10, 742. [Google Scholar] [CrossRef]
- Timmer, W.; Van Rooij, R. Summary of the delft university wind turbine dedicated airfoils. J. Sol. Energy Eng. 2003, 125, 488–496. [Google Scholar] [CrossRef]
- Bai, J.Y.; Zhang, L.; Xingxing, L.I.; Yang, K. Analyzing the effect of wind tunnel wall on the aerodynamic performance of airfoils. Sci. Sin. 2016, 46, 124707. (In Chinese) [Google Scholar]
- Poirel, D.; Métivier, V.; Dumas, G. Computational aeroelastic simulations of self-sustained pitch oscillations of a naca0012 at transitional reynolds numbers. J. Fluids Struct. 2011, 27, 1262–1277. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications, 2nd ed.; Elsevier: New York, NY, USA, 2005; pp. 1–4. [Google Scholar]
- Hand, B.; Kelly, G.; Cashman, A. Numerical simulation of a vertical axis wind turbine airfoil experiencing dynamic stall at high reynolds numbers. Comput. Fluids 2017, 149, 12–30. [Google Scholar] [CrossRef]
- Liu, X.; Lu, C.; Liang, S.; Godbole, A.; Chen, Y. Vibration-induced aerodynamic loads on large horizontal axis wind turbine blades. Appl. Energy 2017, 185, 1109–1119. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Ingham, D.B.; Ma, L.; Pourkashanian, M.; Tao, Z. Turbulence modeling of deep dynamic stall at relatively low reynolds number. J. Fluids Struct. 2012, 33, 191–209. [Google Scholar] [CrossRef]
- Gharali, K.; Johnson, D.A. Numerical modeling of an s809 airfoil under dynamic stall, erosion and high reduced frequencies. Appl. Energy 2012, 93, 45–52. [Google Scholar] [CrossRef]
- Karbasian, H.R.; Esfahani, J.A.; Barati, E. Effect of acceleration on dynamic stall of airfoil in unsteady operating conditions. Wind Energy 2016, 19, 17–33. [Google Scholar] [CrossRef]
- Ansys Fluent 14 User’s Guide; Ansys Inc.: Canonsburg, PA, USA, 2011.
- Durbin, P.A.; Reif, B.P. Statistical Theory and Modeling for Turbulent Flows; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 1119957524. [Google Scholar]
- White, F.M. Fluid mechanics, 7th ed.; McGraw-Hill: New York, NY, USA, 2011; ISBN 978-0-07-352934-9. [Google Scholar]
- Raffel, M.; Favier, D.; Berton, E.; Rondot, C.; Nsimba, M.; Geissler, W. Micro-piv and eldv wind tunnel investigations of the laminar separation bubble above a helicopter blade tip. Meas. Sci. Technol. 2005, 17, 1–13. [Google Scholar] [CrossRef]
- Barakos, G.N.; Drikakis, D. Computational study of unsteady turbulent flows around oscillating and ramping aerofoils. Int. J. Numer. Methods Fluids 2010, 42, 163–186. [Google Scholar] [CrossRef]
- Martinat, G.; Braza, M.; Hoarau, Y.; Harran, G. Turbulence modelling of the flow past a pitching naca0012 airfoil at 105 and 106 reynolds numbers. J. Fluids Struct. 2008, 24, 1294–1303. [Google Scholar] [CrossRef]














| Grid | Suction Surface | Pressure Surface | Trailing Edge | Total Grids |
|---|---|---|---|---|
| G1 | 50 1 | 50 | 11 | 25,753 |
| G2 | 100 | 100 | 11 | 45,387 |
| G3 | 150 | 150 | 11 | 67,238 |
| G4 | 200 | 200 | 11 | 89,070 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhang, L.; Yang, K.; Xu, J.; Li, X. Aerodynamic Performance of Wind Turbine Airfoil DU 91-W2-250 under Dynamic Stall. Appl. Sci. 2018, 8, 1111. https://doi.org/10.3390/app8071111
Li S, Zhang L, Yang K, Xu J, Li X. Aerodynamic Performance of Wind Turbine Airfoil DU 91-W2-250 under Dynamic Stall. Applied Sciences. 2018; 8(7):1111. https://doi.org/10.3390/app8071111
Chicago/Turabian StyleLi, Shuang, Lei Zhang, Ke Yang, Jin Xu, and Xue Li. 2018. "Aerodynamic Performance of Wind Turbine Airfoil DU 91-W2-250 under Dynamic Stall" Applied Sciences 8, no. 7: 1111. https://doi.org/10.3390/app8071111
APA StyleLi, S., Zhang, L., Yang, K., Xu, J., & Li, X. (2018). Aerodynamic Performance of Wind Turbine Airfoil DU 91-W2-250 under Dynamic Stall. Applied Sciences, 8(7), 1111. https://doi.org/10.3390/app8071111





