Coherent Optical Field Manipulation and Optical Information Processing Based on Electromagnetically-Induced Transparency Effect in Pr3+:Y2SiO5 Crystal
Abstract
:1. Introduction
2. Materials and Experimental Setup
3. EIT Effect and Light Pulse Storage via Atomic Coherence Gratings
4. Coherent Manipulation on Light Fields via Atomic Coherence Gratings
4.1. Nondegenerate Phase-Conjugate Wave
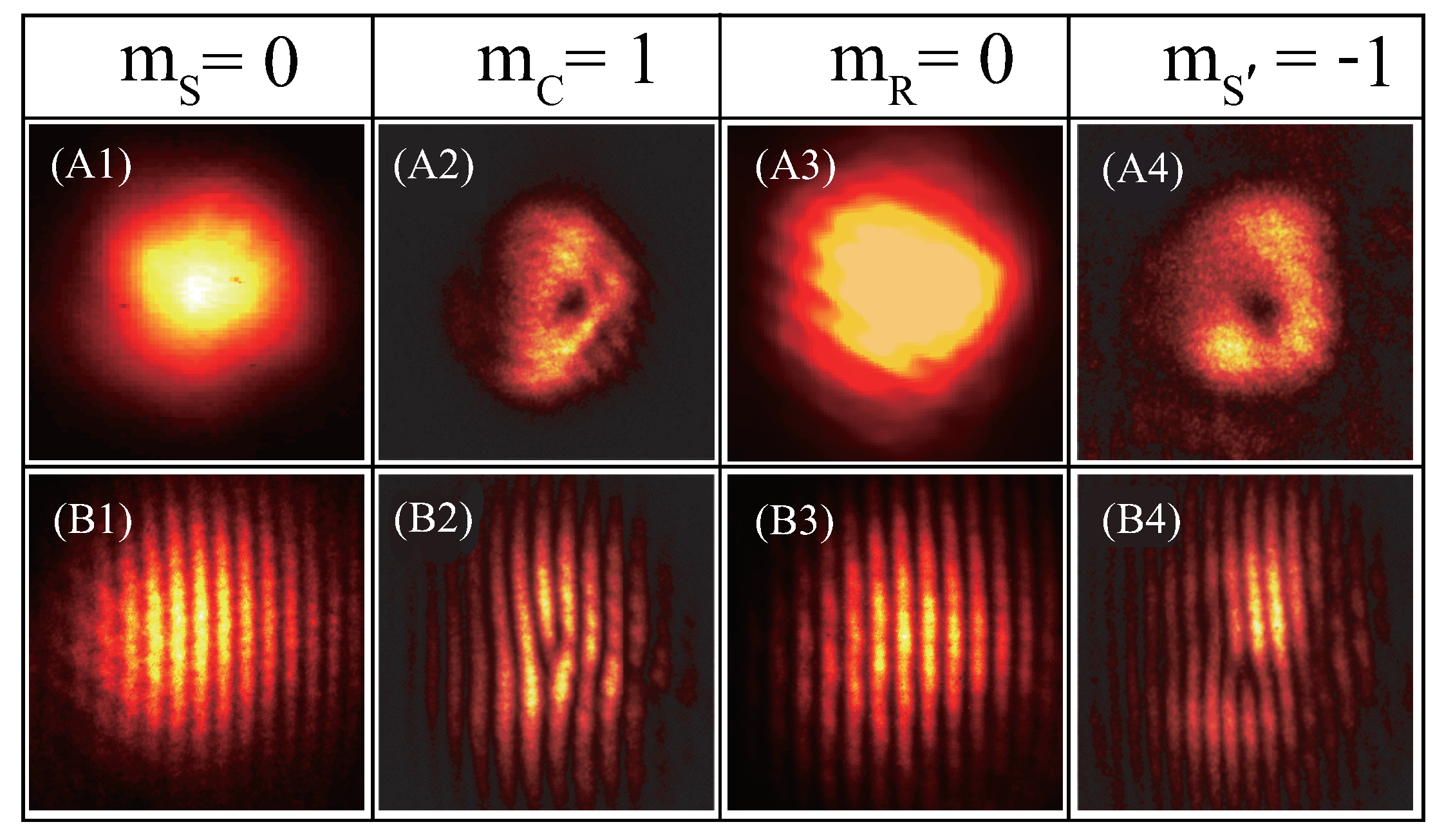
4.2. Manipulation on Optical Vortexes
4.3. First-Order Subwavelength Interference
4.4. Direct Optical Convolution Operation
5. Controllable Polarization Rotator
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EIT | Electromagnetically-induced transparency |
| iCCD | Intensified charge-coupled device |
| AOM | Acousto-optic modulator |
| FWHM | Full width at half maximum |
| OTC | Optical topological charges |
References
- Harris, S.E.; Field, J.E.; Imamoglu, A. Nonlinear optical processes using electromagnetically induced transparency. Phys. Rev. Lett. 1990, 64, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
- Boller, K.; Imamolu, A.; Harris, S.E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 1991, 66, 2593–2596. [Google Scholar] [CrossRef] [PubMed]
- Harris, S.E. Electromagnetically induced transparency. Phys. Today 1997, 50, 36–42. [Google Scholar] [CrossRef]
- Autler, S.H.; Townes, C.H. Stark Effect in Rapidly Varying Fields. Phys. Rev. 1955, 100, 703–722. [Google Scholar] [CrossRef]
- Peng, B.; Ozdemir, S.K.; Chen, W.; Nori, F.; Yang, L. What is and what is not electromagnetically induced transparency in whispering-gallery microcavities. Nat. Commun. 2014, 5, 5082. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Q.C.; Li, T.F.; Luo, X.Q.; Zhao, H.; Xiong, W.; Zhang, Y.S.; Chen, Z.; Liu, J.S.; Chen, W.; Nori, F.; et al. Method for identifying electromagnetically induced transparency in a tunable circuit quantum electrodynamics system. Phys. Rev. A 2016, 93, 053838. [Google Scholar] [CrossRef]
- Sun, H.C.; Liu, Y.X.; Ian, H.; You, J.Q.; Il’ichev, E.; Nori, F. Electromagnetically induced transparency and Autler-Townes splitting in superconducting flux quantum circuits. Phys. Rev. A 2014, 89, 063822. [Google Scholar] [CrossRef]
- Hau, L.V.; Harris, S.E.; Dutton, Z.; Behroozi, C.H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 1999, 397, 594–598. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. [Google Scholar] [CrossRef] [Green Version]
- Marangos, J.P. Electromagnetically induced transparency. J. Mod. Opt. 1998, 45, 471–503. [Google Scholar] [CrossRef]
- Goldfarb, F.; Lauprêtre, T.; Ruggiero, J.; Bretenaker, F.; Ghosh, J.; Ghosh, R. Electromagnetically-induced transparency, slow light, and negative group velocities in a room temperature vapor of 4He*. Comptes Rendus Phys. 2009, 10, 919–926. [Google Scholar] [CrossRef]
- Amari, A.; Walther, A.; Sabooni, M.; Huang, M.; Kroll, S.; Afzelius, M.; Usmani, I.; Lauritzen, B.; Sangouard, N.; de Riedmatten, H.; et al. Towards an efficient atomic frequency comb quantum memory. J. Lumin. 2010, 130, 1579–1585. [Google Scholar] [CrossRef] [Green Version]
- Bonarota, M.; Le Gouet, J.L.; Moiseev, S.A.; Chaneliere, T. Atomic frequency comb storage as a slow-light effect. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 124002. [Google Scholar] [CrossRef] [Green Version]
- Chaneliere, T.; Ruggiero, J.; Bonarota, M.; Afzelius, M.; Le Gouet, J.L. Efficient light storage in a crystal using an atomic frequency comb. New J. Phys. 2010, 12, 023025. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Bo, F.; Dong, R.; Xu, J. Phase-coupling-induced ultraslow light propagation in solids at room temperature. Phys. Rev. Lett. 2004, 93, 133903. [Google Scholar] [CrossRef] [PubMed]
- Podivilov, E.; Sturman, B.; Shumelyuk, A.; Odoulov, S. Light Pulse Slowing Down up to 0.025 cm/s by Photorefractive Two-Wave Coupling. Phys. Rev. Lett. 2003, 91, 083902. [Google Scholar] [CrossRef] [PubMed]
- Bigelow, M.S.; Lepeshkin, N.N.; Boyd, R.W. Superluminal and slow light propagation in a room-temperature solid. Science 2003, 301, 200–202. [Google Scholar] [CrossRef] [PubMed]
- Piredda, G.; Boyd, R.W. Slow light by means of coherent population oscillations: Laser linewidth effects. J. Eur. Opt. Soc.-Rapid Publ. 2007, 2, 07004. [Google Scholar] [CrossRef]
- McMillan, J.F.; Yang, X.; Panoiu, N.C.; Osgood, R.M.; Wong, C.W. Enhanced stimulated Raman scattering in slow-light photonic crystal waveguides. Opt. Lett. 2006, 31, 1235–1237. [Google Scholar] [CrossRef] [PubMed]
- Okawachi, Y.; Bigelow, M.S.; Sharping, J.E.; Zhu, Z.; Schweinsberg, A.; Gauthier, D.J.; Boyd, R.W.; Gaeta, A.L. Tunable all-optical delays via Brillouin slow light in an optical fiber. Phys. Rev. Lett. 2005, 94, 153902. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Dutton, Z.; Behroozi, C.H.; Hau, L.V. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature 2001, 409, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Turukhin, A.V.; Sudarshanam, V.S.; Shahriar, M.S.; Musser, J.A.; Ham, B.S.; Hemmer, P.R. Observation of Ultraslow and Stored Light Pulses in a Solid. Phys. Rev. Lett. 2001, 88, 023602. [Google Scholar] [CrossRef] [PubMed]
- Vudyasetu, P.K.; Camacho, R.M.; Howell, J.C. Storage and retrieval of multimode transverse images in hot atomic Rubidium vapor. Phys. Rev. Lett. 2008, 100, 123903. [Google Scholar] [CrossRef] [PubMed]
- Tu, Y.; Zhang, G.; Zhai, Z.; Xu, J. Angular multiplexing storage of light pulses and addressable optical buffer memory in Pr3+:Y2SiO5 based on electromagnetically induced transparency. Phys. Rev. A 2009, 80, 033816. [Google Scholar] [CrossRef]
- Eisaman, M.D.; Andre, A.; Massou, F.; Fleischhauer, M.; Zibrov, A.S.; Lukin, M.D. Electromagnetically induced transparency with tunable single-photon pulses. Nature 2005, 438, 837–841. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Jin, X.M.; Yang, J.; Dai, H.N.; Yang, S.J.; Zhao, T.M.; Rui, J.; He, Y.; Jiang, X.; Yang, F.; Pan, G.S.; et al. Preparation and storage of frequency-uncorrelated entangled photons from cavity-enhanced spontaneous parametric downconversion. Nat. Photonics 2011, 5, 628–632. [Google Scholar] [CrossRef]
- Ding, D.S.; Zhou, Z.Y.; Shi, B.S.; Guo, G.C. Single-photon-level quantum image memory based on cold atomic ensembles. Nat. Commun. 2013, 4, 2527. [Google Scholar] [CrossRef] [PubMed]
- Nicolas, A.; Veissier, L.; Giner, L.; Giacobino, E.; Maxein, D.; Laurat, J. A quantum memory for orbital angular momentum photonic qubits. Nat. Photonics 2014, 8, 234–238. [Google Scholar] [CrossRef] [Green Version]
- Hsiao, Y.F.; Tsai, P.J.; Chen, H.S.; Lin, S.X.; Hung, C.C.; Lee, C.H.; Chen, Y.H.; Chen, Y.F.; Yu, I.A.; Chen, Y.C. Highly Efficient Coherent Optical Memory Based on Electromagnetically Induced Transparency. Phys. Rev. Lett. 2018, 120, 183602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, L.; Liu, Y.X.; Yi, S.; Sun, C.P.; Nori, F. Control of photon propagation via electromagnetically induced transparency in lossless media. Phys. Rev. A 2007, 75, 063818. [Google Scholar] [CrossRef]
- Chang, Y.; Shi, T.; Liu, Y.X.; Sun, C.P.; Nori, F. Multistability of electromagnetically induced transparency in atom-assisted optomechanical cavities. Phys. Rev. A 2011, 83, 063826. [Google Scholar] [CrossRef] [Green Version]
- Ian, H.; Liu, Y.x.; Nori, F. Tunable electromagnetically induced transparency and absorption with dressed superconducting qubits. Phys. Rev. A 2010, 81, 063823. [Google Scholar] [CrossRef]
- Liu, Y.X.; Xu, X.W.; Miranowicz, A.; Nori, F. From blockade to transparency: Controllable photon transmission through a circuit-QED system. Phys. Rev. A 2014, 89, 043818. [Google Scholar] [CrossRef]
- Gu, X.; Huai, S.N.; Nori, F.; Liu, Y.X. Polariton states in circuit QED for electromagnetically induced transparency. Phys. Rev. A 2016, 93, 063827. [Google Scholar] [CrossRef]
- Kuzmich, A.; Bowen, W.P.; Boozer, A.D.; Boca, A.; Chou, C.W.; Duan, L.M.; Kimble, H.J. Generation of nonclassical photon pairs for scalable quantum communication with atomic ensembles. Nature 2003, 423, 731–734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gorshkov, A.V.; Jiang, L.; Greiner, M.; Zoller, P.; Lukin, M.D. Coherent quantum optical control with subwavelength resolution. Phys. Rev. Lett. 2008, 100, 093005. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Sautenkov, V.A.; Kash, M.M.; Sokolov, A.V.; Welch, G.R.; Rostovtsev, Y.V.; Zubairy, M.S.; Scully, M.O. Optical imaging beyond the diffraction limit via dark states. Phys. Rev. A 2008, 78, 013803. [Google Scholar] [CrossRef] [Green Version]
- Verma, O.N.; Zhang, L.; Evers, J.; Dey, T.N. Optical cloning of arbitrary images beyond the diffraction limits. Phys. Rev. A 2013, 88, 013810. [Google Scholar] [CrossRef]
- Firstenberg, O.; London, P.; Shuker, M.; Ron, A.; Davidson, N. Elimination, reversal and directional bias of optical diffraction. Nat. Phys. 2009, 5, 665–668. [Google Scholar] [CrossRef] [Green Version]
- Firstenberg, O.; Shuker, M.; Davidson, N.; Ron, A. Elimination of the diffraction of arbitrary images imprinted on slow light. Phys. Rev. Lett. 2009, 102, 043601. [Google Scholar] [CrossRef] [PubMed]
- Pugatch, R.; Shuker, M.; Firstenberg, O.; Ron, A.; Davidson, N. Topological stability of stored optical vortices. Phys. Rev. Lett. 2007, 98, 203601. [Google Scholar] [CrossRef] [PubMed]
- Moretti, D.; Felinto, D.; Tabosa, J.W.R. Collapses and revivals of stored orbital angular momentum of light in a cold-atom ensemble. Phys. Rev. A 2009, 79, 023825. [Google Scholar] [CrossRef]
- Zhai, Z.H.; Li, Z.X.; Xu, J.J.; Zhang, G.Q. Transfer and computation of optical topological charges via light pulse buffer memory in an electromagnetically-induced-transparency solid. Phys. Rev. A 2013, 88, 035807. [Google Scholar] [CrossRef]
- Li, Y.Q.; Xiao, M. Enhancement of nondegenerate four-wave mixing based on electromagnetically induced transparency in rubidium atoms. Opt. Lett. 1996, 21, 1064–1066. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, H.; Imamoglu, A. Giant Kerr nonlinearities obtained by electromagnetically induced transparency. Opt. Lett. 1996, 21, 1936–1938. [Google Scholar] [CrossRef] [PubMed]
- Jain, M.; Xia, H.; Yin, G.Y.; Merriam, A.J.; Harris, S.E. Efficient Nonlinear Frequency Conversion with Maximal Atomic Coherence. Phys. Rev. Lett. 1996, 77, 4326–4329. [Google Scholar] [CrossRef] [PubMed]
- Ham, B.S.; Shahriar, M.S.; Hemmer, P.R. Enhancement of four-wave mixing and line narrowing by use of quantum coherence in an optically dense double-Lambda solid. Opt. Lett. 1999, 24, 86–88. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Goorskey, D.; Xiao, M. Enhanced Kerr nonlinearity via atomic coherence in a three-level atomic system. Phys. Rev. Lett. 2001, 87, 073601. [Google Scholar] [CrossRef] [PubMed]
- Harris, S.E.; Field, J.E.; Kasapi, A. Dispersive properties of electromagnetically induced transparency. Phys. Rev. A 1992, 46, R29–R32. [Google Scholar] [CrossRef] [PubMed]
- Xiao, M.; Li, Y.Q.; Jin, S.Z.; Gea-Banacloche, J. Measurement of Dispersive Properties of Electromagnetically Induced Transparency in Rubidium Atoms. Phys. Rev. Lett. 1995, 74, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Richard, R. Moseley, Sara Shepherd, D.J.F.B.D.S.; Dunn, M.H. Electromagnetically-induced focusing. Phys. Rev. A 1996, 53, 408–415. [Google Scholar]
- Liu, X.J.; Jing, H.; Ge, M.L. Solitons formed by dark-state polaritons in an electromagnetic induced transparency. Phys. Rev. A 2004, 70, 055802. [Google Scholar] [CrossRef]
- Min, X.; Hai, W.; Goorskey, D. Light controlling light with enhanced Kerr nonlinearity. Opt. Photonics News 2002, 13, 44–60. [Google Scholar]
- Lukin, M.D.; Imamoglu, A. Controlling photons using electromagnetically induced transparency. Nature 2001, 413, 273–276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Firstenberg, O.; Shuker, M.; Pugatch, R.; Fredkin, D.R.; Davidson, N.; Ron, A. Theory of thermal motion in electromagnetically induced transparency: Effects of diffusion, Doppler broadening, and Dicke and Ramsey narrowing. Phys. Rev. A 2008, 77, 043830. [Google Scholar] [CrossRef] [Green Version]
- Heinze, G.; Hubrich, C.; Halfmann, T. Stopped light and image storage by electromagnetically induced transparency up to the regime of one minute. Phys. Rev. Lett. 2013, 111, 033601. [Google Scholar] [CrossRef] [PubMed]
- Zhong, M.; Hedges, M.P.; Ahlefeldt, R.L.; Bartholomew, J.G.; Beavan, S.E.; Wittig, S.M.; Longdell, J.J.; Sellars, M.J. Optically addressable nuclear spins in a solid with a six-hour coherence time. Nature 2015, 517, 177–180. [Google Scholar] [CrossRef] [PubMed]
- Equall, R.W.; Cone, R.L.; Macfarlane, R.M. Homogeneous broadening and hyperfine structure of optical transitions in Pr3+:Y2SiO5. Phys. Rev. B 1995, 52, 3963–3969. [Google Scholar] [CrossRef]
- Holliday, K.; Croci, M.; Vauthey, E.; Wild, U.P. Spectral hole-burnning and holography in an Y2SiO5:Pr3+ Crystal. Phys. Rev. B 1993, 47, 14741–14752. [Google Scholar] [CrossRef]
- Nilsson, M.; Rippe, L.; Kröll, S.; Klieber, R.; Suter, D. Hole-burning techniques for isolation and study of individual hyperfine transitions in inhomogeneously broadened solids demonstrated in Pr3+:Y2SiO5. Phys. Rev. B 2004, 70, 214116. [Google Scholar] [CrossRef]
- Ham, B.S.; Hemmer, P.; Shahriar, M. Efficient electromagnetically induced transparency in a rare-earth doped crystal. Opt. Commun. 1997, 144, 227–230. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Lukin, M.D. Dark-state polaritons in electromagnetically induced transparency. Phys. Rev. Lett. 2000, 84, 5094–5097. [Google Scholar] [CrossRef] [PubMed]
- Zhai, Z.H.; Dou, Y.L.; Xu, J.J.; Zhang, G.Q. Nondegenerate phase-conjugate wave via stored atomic coherence based on electromagnetically induced transparency in solids. Phys. Rev. A 2011, 83, 043825. [Google Scholar] [CrossRef]
- Flax, S.; O’Donnell, M. Phase-aberration correction using signals from point reflectors and diffuse scatterers: Basic principles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1988, 35, 758–767. [Google Scholar] [CrossRef] [PubMed]
- O’donnell, M.; Flax, S. Phase-aberration correction using signals from point reflectors and diffuse scatterers: Measurements. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1988, 35, 768–774. [Google Scholar] [CrossRef] [PubMed]
- He, G.S. Optical phase conjugation: Principles, techniques, and applications. Prog. Quantum Electron. 2002, 26, 131–191. [Google Scholar] [CrossRef]
- Yariv, A. Three-dimensional pictorial transmission in optical fibers. Appl. Phys. Lett. 1976, 28, 88–89. [Google Scholar] [CrossRef] [Green Version]
- Avizonis, P.V.; Hopf, F.A.; Bomberger, W.D.; Jacobs, S.F.; Tomita, A.; Womack, K.H. Optical phase conjugation in a lithium formate crystal. Appl. Phys. Lett. 1977, 31, 435–437. [Google Scholar] [CrossRef]
- Bloom, D.M.; Bjorklund, G.C. Conjugate wave-front generation and image reconstruction by four-wave mixing. Appl. Phys. Lett. 1977, 31, 592–594. [Google Scholar] [CrossRef]
- Hellwarth, R.W. Generation of time-reversed wave fronts by nonlinear refraction. J. Opt. Soc. Am. 1977, 67, 1–3. [Google Scholar] [CrossRef]
- Heer, C.V.; Griffen, N.C. Generation of a phase-conjugate wave in the forward direction with thin Na-vapor cells. Opt. Lett. 1979, 4, 239–241. [Google Scholar] [CrossRef] [PubMed]
- Khyzniak, A.; Kondilenko, V.; Kucherov, Y.; Lesnik, S.; Odoulov, S.; Soskin, M. Phase conjugation by degenerate forward four-wave mixing. J. Opt. Soc. Am. A 1984, 1, 169–175. [Google Scholar] [CrossRef]
- Feinberg, J. Self-pumped, continuous-wave phase conjugator using internal reflection. Opt. Lett. 1982, 7, 486–488. [Google Scholar] [CrossRef] [PubMed]
- Chiao, R.Y.; Townes, C.H.; Stoicheff, B.P. Stimulated Brillouin scattering and coherent generation of intense hypersonic waves. Phys. Rev. Lett. 1964, 12, 592–595. [Google Scholar] [CrossRef]
- He, G.S.; Prasad, P.N. Stimulated Kerr scattering and reorientation work of molecules in liquid CS2. Phys. Rev. A 1990, 41, 2687–2697. [Google Scholar] [CrossRef] [PubMed]
- Koptev, V.G.; Lazaruk, A.M.; Petrovich, I.P.; Rubanov, A.S. Wavefront inversion in superradiance. JETP Lett. 1978, 28, 434–436. [Google Scholar]
- He, G.S.; Cui, Y.; Yoshida, M.; Prasad, P.N. Phase-conjugate backward stimulated emission from a two-photon-pumped lasing medium. Opt. Lett. 1997, 22, 10–12. [Google Scholar] [CrossRef] [PubMed]
- Griffen, N.C.; Heer, C.V. Focusing and phase conjugation of photon echoes in Na vapor. Appl. Phys. Lett. 1978, 33, 865–866. [Google Scholar] [CrossRef]
- Shiren, N.S. Generation of time-reversed optical wave fronts by backward-wave photon echoes. Appl. Phys. Lett. 1978, 33, 299–300. [Google Scholar] [CrossRef]
- Ham, B.S.; Hemmer, P.R.; Shahriar, M.S. Efficient phase conjugation via two-photon coherence in an optically dense crystal. Phys. Rev. A 1999, 59, R2583–R2586. [Google Scholar] [CrossRef]
- Zibrov, A.S.; Matsko, A.B.; Kocharovskaya, O.; Rostovtsev, Y.V.; Welch, G.R.; Scully, M.O. Transporting and Time Reversing Light via Atomic Coherence. Phys. Rev. Lett. 2002, 88, 103601. [Google Scholar] [CrossRef] [PubMed]
- Soskin, M.; Vasnetsov, M. Singular optics. Prog. Opt. 2001, 42, 219–276. [Google Scholar]
- Dennis, M.R.; O’Holleran, K.; Padgett, M.J. Singular Optics: Optical Vortices and Polarization Singularities. Prog. Opt. 2009, 53, 293–363. [Google Scholar]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonic 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Franke-Arnold, S.; Allen, L.; Padgett, M. Advances in optical angular momentum. Laser Photonics Rev. 2008, 2, 299–313. [Google Scholar] [CrossRef]
- Shi, B.S.; Ding, D.S.; Zhang, W. Quantum storage of orbital angular momentum entanglement in cold atomic ensembles. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 032004. [Google Scholar] [CrossRef] [Green Version]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Boto, A.N.; Kok, P.; Abrams, D.S.; Braunstein, S.L.; Williams, C.P.; Dowling, J.P. Quantum Interferometric Optical Lithography: Exploiting Entanglement to Beat the Diffraction Limit. Phys. Rev. Lett. 2000, 85, 2733–2736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitchell, M.W.; Lundeen, J.S.; Steinberg, A.M. Super-resolving phase measurements with a multiphoton entangled state. Nature 2004, 429, 161–164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walther, P.; Pan, J.W.; Aspelmeyer, M.; Ursin, R.; Gasparoni, S.; Zeilinger, A. De Broglie wavelength of a non-local four-photon state. Nature 2004, 429, 158–161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boyd, R.W.; Dowling, J.P. Quantum lithography: Status of the field. Quantum Inf. Proc. 2012, 11, 891–901. [Google Scholar] [CrossRef]
- Jacobson, J.; Björk, G.; Chuang, I.; Yamamoto, Y. Photonic de Broglie Waves. Phys. Rev. Lett. 1995, 74, 4835–4838. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.J.S.; Monken, C.H.; Pádua, S. Measurement of the de Broglie Wavelength of a Multiphoton Wave Packet. Phys. Rev. Lett. 1999, 82, 2868–2871. [Google Scholar] [CrossRef]
- Edamatsu, K.; Shimizu, R.; Itoh, T. Measurement of the Photonic de Broglie Wavelength of Entangled Photon Pairs Generated by Spontaneous Parametric Down-Conversion. Phys. Rev. Lett. 2002, 89, 213601. [Google Scholar] [CrossRef] [PubMed]
- Scarcelli, G.; Valencia, A.; Shih, Y. Two-photon interference with thermal light. Europhys. Lett. 2004, 68, 618–624. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Cao, D.Z.; Huang, F.; Li, H.G.; Sun, X.J.; Wang, K. Experimental Observation of Classical Subwavelength Interference with a Pseudothermal Light Source. Phys. Rev. Lett. 2005, 94, 173601. [Google Scholar] [CrossRef] [PubMed]
- Oppel, S.; Buttner, T.; Kok, P.; von Zanthier, J. Superresolving multiphoton interferences with independent light sources. Phys. Rev. Lett. 2012, 109, 233603. [Google Scholar] [CrossRef] [PubMed]
- Hong, P.L.; Zhang, G.Q. Subwavelength interference with an effective entangled source. Phys. Rev. A 2013, 88, 043838. [Google Scholar] [CrossRef]
- Hong, P.; Zhang, G. Synchronous position two-photon interference of random-phase grating. J. Opt. Soc. Am. A 2015, 32, 1256–1261. [Google Scholar] [CrossRef] [PubMed]
- Hong, P.; Zhang, G. Super-resolved optical lithography with phase controlled source. Phys. Rev. A 2015, 91, 053830. [Google Scholar] [CrossRef]
- Ito, T.; Okazaki, S. Pushing the limits of lithography. Nature 2000, 406, 1027–1031. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, J.; Fan, H.; Liu, J.; Zhang, G. High visibility first-order subwavelength interference based on light pulse storage via electromagnetically induced transparency. Sci. Rep. 2017, 7, 2361. [Google Scholar] [CrossRef] [PubMed]
- Brooker, G. Modern Classical Optics; Oxford University: Oxford, UK, 2003. [Google Scholar]
- Li, Z.; Liu, J.; Fan, H.; Zhang, G. Study on Convolution Operation of Optical Information via Quantum Storage. Acta Opt. Sin. 2017, 37, 91–96. [Google Scholar]
- Boileau, J.C.; Gottesman, D.; Laflamme, R.; Poulin, D.; Spekkens, R.W. Robust polarization-based quantum key distribution over a collective-noise channel. Phys. Rev. Lett. 2004, 92, 017901. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.Z.; Zhang, J.; Yang, D.; Gao, W.B.; Ma, H.X.; Yin, H.; Zeng, H.P.; Yang, T.; Wang, X.B.; Pan, J.W. Experimental long-distance decoy-state quantum key distribution based on polarization encoding. Phys. Rev. Lett. 2007, 98, 010505. [Google Scholar] [CrossRef] [PubMed]
- Bloch, M.; McLaughlin, S.W.; Merolla, J.M.; Patois, F. Frequency-coded quantum key distribution. Opt. Lett. 2007, 32, 301–303. [Google Scholar] [CrossRef] [PubMed]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spedalieri, F.M. Quantum key distribution without reference frame alignment: Exploiting photon orbital angular momentum. Opt. Commun. 2006, 260, 340–346. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.X.; Liu, J.J.; Yu, P.; Zhang, G.Q. Birefringence and polarization rotator induced by electromagnetically induced transparency in rare earth ion-doped crystals. Appl. Phys. B 2016, 122, 109. [Google Scholar] [CrossRef]
- Wielandy, S.; Gaeta, A.L. Coherent Control of the Polarization of an Optical Field. Phys. Rev. Lett. 1998, 81, 3359–3362. [Google Scholar] [CrossRef]
- Wang, B.; Li, S.; Ma, J.; Wang, H.; Peng, K.; Xiao, M. Controlling the polarization rotation of an optical field via asymmetry in electromagnetically induced transparency. Phys. Rev. A 2006, 73, 051801(R). [Google Scholar] [CrossRef]
- Drampyan, R.; Pustelny, S.; Gawlik, W. Electromagnetically induced transparency versus nonlinear Faraday effect: Coherent control of light-beam polarization. Phys. Rev. A 2009, 80, 033815. [Google Scholar] [CrossRef]










© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, Z.; Fan, H.; Zhang, G. Coherent Optical Field Manipulation and Optical Information Processing Based on Electromagnetically-Induced Transparency Effect in Pr3+:Y2SiO5 Crystal. Appl. Sci. 2018, 8, 1179. https://doi.org/10.3390/app8071179
Liu J, Li Z, Fan H, Zhang G. Coherent Optical Field Manipulation and Optical Information Processing Based on Electromagnetically-Induced Transparency Effect in Pr3+:Y2SiO5 Crystal. Applied Sciences. 2018; 8(7):1179. https://doi.org/10.3390/app8071179
Chicago/Turabian StyleLiu, Jianji, Zhixiang Li, Hongming Fan, and Guoquan Zhang. 2018. "Coherent Optical Field Manipulation and Optical Information Processing Based on Electromagnetically-Induced Transparency Effect in Pr3+:Y2SiO5 Crystal" Applied Sciences 8, no. 7: 1179. https://doi.org/10.3390/app8071179
APA StyleLiu, J., Li, Z., Fan, H., & Zhang, G. (2018). Coherent Optical Field Manipulation and Optical Information Processing Based on Electromagnetically-Induced Transparency Effect in Pr3+:Y2SiO5 Crystal. Applied Sciences, 8(7), 1179. https://doi.org/10.3390/app8071179



