Next Article in Journal
Topological Network Properties of Fractal-Like Metallic Nanoparticle Patterns and Their Effects on Optical Resonances
Previous Article in Journal
Battery State Estimation for Lead-Acid Batteries under Float Charge Conditions by Impedance: Benchmark of Common Detection Methods
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 8
Issue 8
10.3390/app8081309
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Computational Fluid Dynamic Accuracy in Mimicking Changes in Blood Hemodynamics in Patients with Acute Type IIIb Aortic Dissection Treated with TEVAR

by
Andrzej Polanczyk
1,2,*,
Aleksandra Piechota-Polanczyk
3,
Christoph Domenig
2,
Josif Nanobachvili
2,
Ihor Huk
2 and
Christoph Neumayer
2
1
Faculty of Process and Environmental Engineering, Lodz University of Technology, Wolczanska 213, 90-924 Lodz, Poland
2
Department of Surgery, Division of Vascular Surgery, Medical University of Vienna, Spitalgasse 23, 1090 Wien, Austria
3
Department of Medical Biotechnology, Faculty of Biochemistry, Biophysics and Biotechnology, Jagiellonian University, Gronostajowa 7, 30-387 Krakow, Poland
*
Author to whom correspondence should be addressed.
Appl. Sci. 2018, 8(8), 1309; https://doi.org/10.3390/app8081309
Submission received: 27 June 2018 / Revised: 28 July 2018 / Accepted: 1 August 2018 / Published: 7 August 2018
(This article belongs to the Section Applied Biosciences and Bioengineering)
Browse Figures
Versions Notes

Abstract

:
Background: We aimed to verify the accuracy of the Computational Fluid Dynamics (CFD) algorithm for blood flow reconstruction for type IIIb aortic dissection (TBAD) before and after thoracic endovascular aortic repair (TEVAR). Methods: We made 3D models of the aorta and its branches using pre- and post-operative CT data from five patients treated for TBAD. The CFD technique was used to quantify the displacement forces acting on the aortic wall in the areas of endograft, mass flow rate/velocity and wall shear stress (WSS). Calculated results were verified with ultrasonography (USG-Doppler) data. Results: CFD results indicated that the TEVAR procedure caused a 7-fold improvement in overall blood flow through the aorta (p = 0.0001), which is in line with USG-Doppler data. A comparison of CFD results and USG-Doppler data indicated no significant change in blood flow through the analysed arteries. CFD also showed a significant increase in flow rate for thoracic trunk and renal arteries, which was in accordance with USG-Doppler data (accuracy 90% and 99.9%). Moreover, we observed a significant decrease in WSS values within the whole aorta after TEVAR compared to pre-TEVAR (1.34 ± 0.20 Pa vs. 3.80 ± 0.59 Pa, respectively, p = 0.0001). This decrease was shown by a significant reduction in WSS and WSS contours in the thoracic aorta (from 3.10 ± 0.27 Pa to 1.34 ± 0.11Pa, p = 0.043) and renal arteries (from 4.40 ± 0.25 Pa to 1.50 ± 0.22 Pa p = 0.043). Conclusions: Post-operative remodelling of the aorta after TEVAR for TBAD improved hemodynamic patterns reflected by flow, velocity and WSS with an accuracy of 99%.

1. Introduction

Aortic diseases represent a clinical relevant problem characterised by a growing annual incidence [1]. Amongst these diseases, acute dissection, with tear formation in the inner lining of the aorta, is one of the worst cardiovascular emergencies, associated with considerable morbidity and mortality [2,3,4]. The concept of using thoracic endovascular aortic repair (TEVAR) for the management of acute type B dissection as an alternative treatment modality to open repair was introduced in the late nineties [5,6].
The onset, generation and progression of aortic dissection can be influenced by mechanical factors including hemodynamic, vascular geometry and mechanical properties of the aortic wall [7,8]. Hemodynamic parameters are believed to play a crucial role in the formation and the progression of the dissection. Blood mass flow rate and wall shear stress (WSS) are the main parameters that change after aortic repair (TEVAR) [7,9]. The blood flow pattern within the dissected aorta is dominated by locally highly disturbed and possibly turbulent flow with strong recirculation [10]. Therefore, in this study we focus on the evaluation of hemodynamic parameters such as mass flow rate and wall stress pre- and post TEVAR.
Computational cardiovascular mechanics has allowed scientists to create complex 3D models for the simulation of cardiovascular problems [11]. With the aid of computational fluid dynamics (CFD), simulations of blood flow in patient-specific aortic models were reported [12,13,14]. Application of computational methods, including the CFD technique in the topic of blood flow in vessels is widely described in literature [15,16]. Previously, the CFD technique has been applied to assess blood flow hemodynamic in vessels after stent-graft implantation in aortic aneurysms [17]. The real three-dimensional geometry of vessels is usually reconstructed with the use of medical data acquired from CT or magnetic resonance imaging [18,19]. Using this approach it is possible to measure hemodynamic parameters within 3D models that provide important information on hemodynamic changes within the true and false lumen after TEVAR for the treatment of acute type B dissection [20].
Therefore, the aim of this study was to verify the accuracy of CFD-calculated changes in blood flow parameters within the aorta and aortic branches in patients with type B aortic dissection (TBAD) before and after TEVAR procedure. Further, we verified numerical results with USG-Doppler data and calculated accuracy by comparing numerical (CFD) and clinical (USG-Doppler) measurements.

2. Materials and Methods

2.1. Materials

In this study we used data collected from 5 male patients aged from 39 to 54 years after CTA (GE Light-Speed 64 VCT; GE Healthcare, Fairfield, CT, USA) and USG-Doppler (GE Vivid 7, GE Healthcare, Fairfield, CT, USA) who underwent treatment with vascular and endovascular procedures at the Medical University of Vienna between 2010–2014. Anonymized by coding information pre-operative (baseline) and post-operative CTA data (512 × 512 × 270 voxels, in-plane resolution of 0.78 × 0.78 mm, slice thickness 1 mm) from the aforementioned patients with acute complicated type B dissection formed the base of this study. Inclusion criteria comprise acute type IIIb aortic dissection that started proximal to the left subclavian artery and involved the renal arteries in each of the cases. Over the years 2010–2014, 7 consecutive patients with acute type B aortic dissection were identified. Of these, 2 had dissection limited to the thoracic aorta and were excluded. All of the remaining 5 with type IIIb dissection had TEVAR intervention and comprised the cohort of this study. The aortic reconstructions comprised implantation of a stent-graft in the distal aortic arch and the descending thoracic aorta (Left subclavian artery (LSA) covered) and the implantation of self-expandable stents into arteries (Table 1). In all analysed cases, the TEVAR procedure led to thrombosis of the false lumen in the area of the descending aorta, which was not covered by the stent. The study was approved by the local Institutional Review Board (2069/2012).

2.2. Computational Fluid Dynamics Analysis

Using Digital Imaging and Communications in Medicine (DICOM) data, patient-specific 3D computer models of the patients′ entire aortas were created as previously described [22,23]. Briefly, on each DICOM picture, areas of interest were marked. Next, 3d reconstruction was built and applied to the CFD analysis. The models included data from the ascending aorta, aortic arch, descending thoracic aorta, abdominal aorta, iliac arteries, the “orifices” of the main aortic branches, the brachiocephalic trunk, carotid arteries, subclavian arteries, renal arteries, iliac arteries, and the endograft and stents placed during TEVAR (Figure 1).
A CFD was utilized to simulate blood flow and WSS for one cardiac cycle as previously described [24]. The vessel wall area was treated as a rigid surface. Reconstruction of blood flow geometry was made using ANSYS ICEM CFD (ANSYS, Canonsburg, PA USA). The number of tetrahedral mesh elements for particular areas depended on individual geometry and changed from 900,000 to 1,000,000. CFD simulations were performed in ANSYS FLUENT 18.2 software (ANSYS, Canonsburg, PA, USA) as previously described [25]. In all cases we assumed that spatial configurations of analysed 3d geometries had one entry to the aorta, three outlets at the aortic arch, and eight in the middle of the aorta and four at the bottom. Moreover, multiple re-entry tears for the dissection part existed in all analysed cases. The mathematical domain was described with the boundary conditions as follow: at the inlet, an assumed condition of blood flow velocity was u = (u,v,w), while at the outlets the condition p = const was taken. We focused on blood hemodynamic changes in arteries where endografts and stents were placed to verify the accuracy of adjustment of calculated numerical results. We used data from USG-Doppler (GE Vivid 7, GE Healthcare, USA) gathered before and after surgical intervention in all patients. Each time inlet boundary condition was taken from USG-Doppler data recorded in the area of ascending aorta before and after surgical intervention. USG-Doppler data were presented as a blood velocity as a function of time including one whole cardiac cycle which was utilized in computer simulations. Moreover, USG-Doppler data were recorded before and after surgical intervention for all 15 different outlets for each analysed patient. Those data were further used for verification of the CFD model. Each time the USG-Doppler probe was placed in the area of the investigated outflow.
To determine the boundary condition for CFD simulations, we prepared sixteen velocity profiles for each patient (one as an inlet boundary and fifteen for the outlets). We also set different pressure values at the outlets. The pressure values were measured for each patient; therefore, realistic resistance from upper and lower vessels that were not reconstructed was included as the pressure outlet boundary. Following Hoskins et al. [26], blood density was assumed as a constant value of 1040 kg/m3. Because of the high cell number and particulate nature of erythrocytes, whole blood exhibits non-Newtonian rheology and belongs to the non-Newtonian liquids group thinning with an increasing value of shear stress. Therefore, Quemada′s model was used to describe the rheological properties of blood [27].
In this paper we concentrated on the comparison of mass flow rate/velocity and WSS for the areas where endografts were placed and where changes in flow velocity and WSS after TEVAR were noticed.
Calculated results were verified with USG-Doppler data gathered from patients before and after the TEVAR procedure. The accuracy was calculated by comparing numerical (CFD) and clinical (USG-Doppler) measurements.

2.3. Statistical Analysis

Statistical analysis was performed using Statistica 12.0 software (Statsoft). Values were presented as mean ± S.E. (standard error) and the median and interquartile range as appropriate. Comparisons between post- and pre-TEVAR were made using the Wilcoxon Ranked Sign test or paired Student’s t test after verifying normality and variance. Results from CFD were compared with USG-Doppler using Spearman’s correlation analysis. Data were considered significantly different when p < 0.05 unless otherwise noted. Moreover, Bland-Altman method analyses were used to analyse the agreement between USG-Doppler and CFD data.

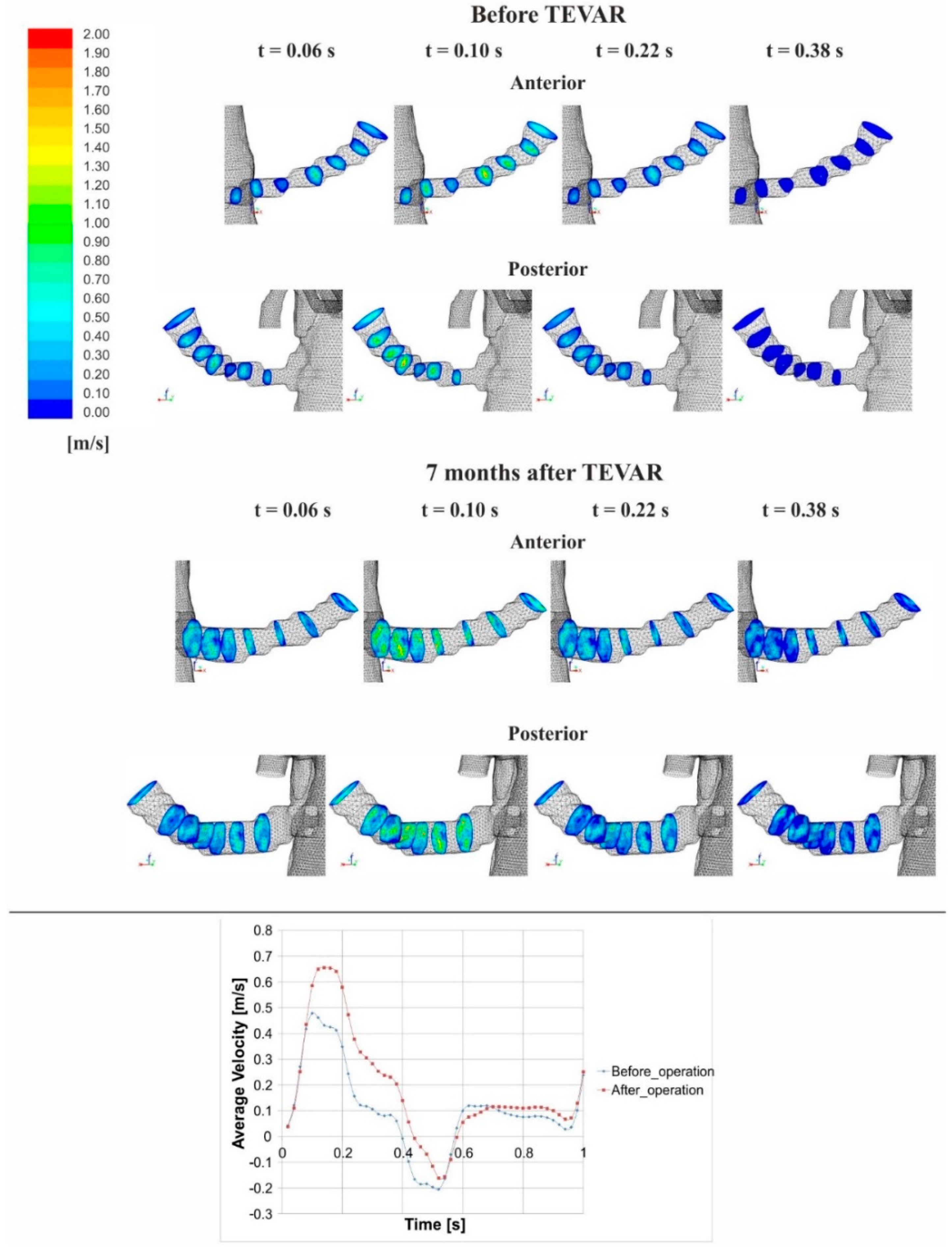
3. Results

3.1. Flow Analysis

The CFD results indicated that in all analysed cases, the TEVAR procedure changed blood hemodynamics in aortic lumen and adjacent branches. As expected after TEVAR, more blood was directed into the true lumen due to complete closure of the false lumen (Table 2). CFD results indicated a 7-fold increase in blood flow through the true lumen after TEVAR compared to pre-TEVAR (62.28 ± 1.23 mL/s and 9.02 ± 0.26 mL/s, respectively, p < 0.0001; Table 2). Calculated results were verified with USG-Doppler data, where an 8-fold increase in blood flow through the true lumen was noticed after TEVAR compared to pre-TEVAR (64.81 ± 0.89 mL/s and 8.07 ± 1.54 mL/s, respectively, p < 0.0001; Table 2). Therefore, we accomplished 96% and 90% accuracy for CFD results compared to USG-Doppler in the post-TEVAR and pre-TEVAR procedures (Table 2).
As post-interventional aortic remodelling contributes to blood flow distribution into aortic branches, we analysed changes in blood flow pre- and post-TEVAR with CFD and compared those results with USG-Doppler data. We recorded flow changes in three branches of the aortic arch—the brachiocephalic trunk, carotid artery and subclavian artery. CFD results indicated no significant change in blood flow through those arteries (Table 2), which was verified with USG-Doppler data (Table 2). The accuracy of CFD calculations in post-TEVAR was 97.8%, 97.7% and 98.5% for the brachiocephalic trunk, carotid artery and subclavian artery, respectively (Table 2) and 99.8%, 99.7%, 99.9% for the brachiocephalic trunk, carotid artery and subclavian artery, respectively, pre-TEVAR (Table 2). There was also a strong positive correlation between CFD and USG-Doppler data for all outflows (r = 0.942, r = 0.906, r = 0.948 for the brachiocephalic trunk, carotid artery and subclavian artery, respectively).
Also, CFD results indicated that catheter stent intervention in renal arteries contributed to a significant increase of blood flow post-TEVAR compared to pre-TEVAR (10.37 ± 0.63 mL/s and 9.33 ± 0.29 mL/s, respectively, p = 0.43; Table 2). This was in line with USG-Doppler data where increased blood flow post-TEVAR compared to pre-TEVAR was observed (9.84 ± 0.46 mL/s and 9.16 ± 0.38 mL/s, respectively, p = 0.043; Table 2). Also, a strong positive relationship between CFD and USG-Doppler data was shown (r = 0.784). Therefore, the accuracy of CFD calculations in post-TEVAR was 95% (Table 2) and 98.2% pre-TEVAR (Table 2).
Finally, no significant change in blood flow in the iliac was detected post-TEVAR compared to pre-TEVAR (2.01 ± 0.07 mL/s and 2.14 ± 0.12 mL/s, respectively, p = 0.079; Table 2). This was in line with USG-Doppler data where blood flow slightly decreased after TEVAR (2.02 ± 0.15 mL/s and 2.24 ± 0.17 mL/s, respectively, p = 0.079; Table 2). The accuracy of CFD calculations post-TEVAR was 99.3% (Table 2) and 95.5% pre-TEVAR (Table 2). Moreover, a strong positive relationship between CFD and USG-Doppler data was shown (r = 0.805).
After detailed analysis of changes in blood flow distribution post- and pre-TEVAR, we decided to analyse changes in blood velocity in two areas of the aorta: the aortic arch, where dissections began in all analysed cases and the renal arteries, where changes in blood flow were highest after TEVAR.
CFD analysis in the area of the true lumen indicated a significant decrease in blood velocity post-TEVAR compared to pre-TEVAR (0.22 ± 0.03 m/s and 0.32 ± 0.01 m/s, respectively, p = 0.043; Table 3). Also, a significant decrease in velocity was observed for USG-Doppler data (0.23 ± 0.03 m/s to 0.29 ± 0.05 m/s, post- and pre-TEVAR, (p = 0.043; Table 3). The accuracy of CFD calculations was 96% post-TEVAR (Table 3) and 90% pre-TEVAR (Table 3). There was a moderate positive relationship between CFD and USG-Doppler data (r = 0.706).
Contrary to the thoracic aorta, calculated blood velocity in renal arteries increased post-TEVAR compared to pre-TEVAR (0.36 ± 0.01 m/s and 0.32 ± 0.01 m/s, respectively, p = 0.043; Table 3). Analysis of USG-Doppler data in the same area confirmed a similar trend (0.34 ± 0.01 m/s vs. 0.32 ± 0.01 m/s post-TEVAR vs. pre-TEVAR, p = 0.043; Table 3). The accuracy of CFD calculations in the renal arteries was 95% post-TEVAR (Table 3) and 97.2% pre-TEVAR (Table 3). Also, a moderate positive relationship between CFD and USG-Doppler data was shown (r = 0.661).
Detailed analysis of changes in blood velocity contours in the aortic arch and the left renal artery pre- and post-TEVAR is presented in Figure 2 and Figure 3, respectively. We observed high-velocity flow in the ascending aorta, with a pronounced jet into the dissection entry tear from the true lumen to the false lumen, and a slow-flow zone with recirculation patterns adjacent to the false lumen wall. Moreover, in our study the dissecting membrane created an artificial barrier characterized by high velocity (Figure 2). Additionally, the post-operative character of velocity contours contours distribution was more uniform, and no cross-sectional flow between the true and false lumen was observed for all five analysed patients (Figure 2). Post-operative remodelling each time increased aortic diameter in the true lumen (Figure 2). Uneven distribution of blood flow contours accompanied by a thinner aortic wall within the dissection area increased the risk of further aortic wall remodelling. Therefore, in all five cases, remodelling with insertion of an endograft in the aortic arch closed the false lumen and directed blood through the true channel that improved blood rheology.
Furthermore, stent implantation led to an increased cross sectional diameter of the left renal artery, therefore ameliorating blood flow and decreasing pressure drag. The endovascular intervention separated the false lumen and directed blood flow through the true lumen leaving one channel. Post-operative remodelling each time increased blood velocity (Figure 3). Therefore, in all five cases, remodelling with insertion of an endograft in the renal artery improved blood rheology.
The difference between clinical and the predicted velocity changes (mL/s) across the aortic branches according to Bland-Altman analysis was 0.17 mL/s (confidence interval equal to 2.76 mL/s). The separate analysis of blood flow changes in the adjacent branches relative to measured values were lower in the case of the thoracic artery (0.95 mL/s; confidence interval equal to 5.85 mL/s), the brachiocephalic trunk (0.01 mL/s; confidence interval equal to 0.89 mL/s) and the iliac arteries (0.10 mL/s; confidence interval equal to 0.55 mL/s), while higher values of calculated blood flow profiles were noticed for the carotid artery (0.02 mL/s; confidence interval equal to 0.74 mL/s) and the renal arteries (0.17 mL/s; confidence interval equal to 2.05 mL/s).

3.2. Stress Analysis

Finally, we analysed changes in WSS to compare distribution of stresses during blood flow before and after TEVAR for the thoracic trunk and renal arteries. We observed a significant decrease in WSS values post-TEVAR compared to pre-TEVAR (1.34 ± 0.20 Pa vs. 3.80 ± 0.59 Pa, respectively, p = 0.0001). This decrease was associated with an increase in true lumen diameter and a decrease in blood velocity in this area.
Moreover, a significant decrease of WSS values was observed in the thoracic aorta post-TEVAR compared to pre-TEVAR (1.34 ± 0.11 Pa and 3.10 ± 0.27 Pa, respectively, p = 0.043). A similar tendency was observed for the renal arteries (1.50 ± 0.22 Pa and 4.40 ± 0.25 Pa, post-TEVAR and pre-TEVAR, respectively, p = 0.043). The changes in WSS contour distribution in the thoracic aorta and left renal artery are presented in Figure 4 and Figure 5, respectively. At each time for all analysed patients, the pre-operative aorta had an irregular shape with numerous narrowing areas and unstable flow forced by the appearance of the two lumens (true and false). In our study the dissecting membrane created an artificial barrier characterized by high-WSS in the areas adjacent to the wall (4.7 Pa, Figure 4). Therefore, in the true lumen, WSS was much lower than expected. The endovascular intervention for all five patients separated the false lumen and directed blood flow through the true lumen leaving one channel. This smoothed the blood flow in each analysed patient and caused a noticeable change in WSS from 3.5 Pa to 1.3 Pa after TEVAR.
The second critical area affected by aorta dissection before TEVAR was the renal arteries. Prior to intervention, the left renal artery had an irregular shape with numerous stenotic areas, which resulted in high average WSS values (4.4 Pa) (Figure 5). The endovascular intervention led to an alignment of the artery and 57% increase in the average channel cross-section. Free passage through the left renal artery also lowered the average WSS in this area (Figure 5). Moreover, there was a 3.2-fold decrease in the average WSS from 4.4 Pa to 1.4 Pa (Figure 5). The distribution of the WSS contours post- and pre-TEVAR is presented in Figure 5. Moreover, in patients where the stent was placed in the left renal artery, WSS decreased by 3.1–2.3 Pa.

4. Discussion

The paper presents a computational approach to standardize the CFD technique for the virtual process of aortic dissection repair with the use of spatial configuration of human vessels. These results demonstrated that CFD simulation can accurately quantify changes in blood distribution, velocity and wall shear stress resulting from aortic remodelling after TEVAR for acute type B dissection.
The results from CFD calculations indicated that the TEVAR procedure improved general blood flow through the aorta and increased blood flow through the thoracic aorta and renal arteries, with a concomitant decrease of blood flow through the brachiocephalic trunk, carotid arteries, subclavian artery and iliac artery. Moreover, calculated values were in accordance with USG-Doppler data, i.e., 99.3 to 90%. Only for renal arteries were USG-Doppler investigations less accurate, but it is well known that exposure of renal arteries (especially in overweight patients) is sometimes difficult with this examination [28]. A similar approach was applied by Cheng et al. who successfully verified computational model with PC MRI [29]. Changes in velocity profiles were based on the changes in spatial configuration of the geometry of aorta and aortic branches. We noticed a higher-velocity profile and better velocity contour distribution in the aortic arch after endograft implantation as well as in the renal and iliac arteries after stenting. It was previously indicated that during dissection, around 80% of stroke volume enters the false lumen, which may further increase the dilation of the aorta [30]. Hence, implantation of an endograft in the thoracic aorta closed the primary entry to the false lumen and improved the flow profile. This is in line with Yu et al. (2016), who noticed that there was no blood flow in the false lumen across the entry after its closure [31]. Moreover, high-flow conditions within the true lumen may stabilize the aortic integrity and limit aneurysm growth, as demonstrated previously [32].
Analysis of 3D geometries confirmed that the appearance of wall dissection had an impact on blood hemodynamics. Higher WSS values and blood flow were observed in the area of dissociation. This is in line with Rudenick et al. who noticed that the existence of tears and their size had an impact on blood flow and velocity [33]. Also, Ahmed et al. indicated that a small tear decreased false lumen flow and velocity [34].
We further showed that the TEVAR procedure decreased the WSS values and changed the WSS contour distribution in the thoracic trunk and renal arteries. Lower WSS within the aorta was a consequence of closure of the primary entry to the false lumen, which began in the aortic arch, and higher cross-sectional diameter of iliac and renal arteries. Previously, Karmonik et al. [35] stated that a tear at the aneurysm entry resulted in high wall shear stress and low total pressure. Also, Cheng et al. [10] reported high values of WSS around the entry tear inside the true lumen, which could increase the likelihood of tear expansion. Moreover, post-operative remodelling of the aorta leads to changes in the lumen cross-sectional diameter, which strongly correlates with peak wall stress [36]. Furthermore, peak wall stress values are influenced by vessel centreline asymmetry and maximum diameter [37]. Therefore, changes in WSS values in the aorta and aortic branches observed in patients treated for TBAD are strongly associated with an improvement of aortic geometry post-TEVAR.

Limitations to the Study

Although our study demonstrates the improvement of mass flow rate/velocity and wall stress after endograft implantation, it has some limitations. Firstly, unlike in humans, we treated the artery wall as a rigid body, therefore assuming that it had negligible influence on blood flow. However, this approach is in line with Duvernois et al. [38], who showed that differences between blood flow distribution for rigid and pulsating walls are comparable. Secondly, we described blood rheological properties using the non-Newtonian shear-thinning Quemada model. This is in accordance with Xiang et al. [39], who showed that non-Newtonian fluid reflects the real properties of blood and does not artificially increase WSS as the Newtonian approach does. Also, we analysed only acute type IIIb aortic dissection and the obtained data may not be applicable for other types of aortic dissections without initial verification. Moreover, small sample size could influence the obtained results. However, the patients were carefully selected; hence, we believe the obtained results may be applicable to similar cases. Finally, the CFD simulation accuracy depends on the resolution of CTA and USG-Doppler data. The higher the resolution, the better the 3d model and the final results of blood hemodynamic reconstruction. In our study we used 1 mm slides from CT scans, which gives an acceptable but not a perfect resolution. Therefore, it might influence the final results. However, given the highly viscous nature of the flow, it is likely that the overall flow patterns would be very similar to those presented here. The obvious next step would be to extend this study and analyse a wider group of patients with TBAD and determine the usefulness of the CFD technique in post-operative patient evaluation.

5. Conclusions

In summary, our study indicates that post-operative remodelling of the aorta after TEVAR for acute type B dissection improved hemodynamic patterns reflected by flow velocity and WSS. The calculated results were accurate, i.e., 90% to 99% with USG-Doppler data.
The proposed algorithm accurately mimic changes in blood distribution and velocity profiles after the TEVAR procedure in patients with TBAD. This model may be of further use pre-operatively to estimate how TEVAR procedures will influence blood hemodynamic in patients with TBAD. Therefore, it may become a useful non-invasive tool for the characterization of hemodynamic changes after endovascular treatment of acute TBAD.

Author Contributions

A.P.: participated in research design, conducted experiments, performed data analysis, wrote the manuscript; A.P.-P.: participated in research design, contributed to the writing of the manuscript; C.D.: participated in research design, contributed to the writing of the manuscript; J.N.: participated in research design and contributed to the writing of the manuscript; I.H.: participated in data analysis and contributed to the writing of the manuscript; C.N.: participated in research design and data analysis, and contributed to the writing of the manuscript.

Funding

The study was supported by the Polish National Centre for Research and Development (501/10-34-19-605 to AP) and by grant number 181110 from the Medical University of Vienna, Department of Surgery (to IH). The Faculty of Biochemistry, Biophysics and Biotechnology of Jagiellonian University is a partner of the Leading National Research Center (KNOW) supported by the Ministry of Science and Higher Education.

Acknowledgments

We would like to thank Prof. M. Funovcs for his contribution to the radiological consultancy.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Olsson, C.; Thelin, S.; Stahle, E.; Ekbom, A.; Granath, F. Thoracic aortic aneurysm and dissection: Increasing prevalence and improved outcomes reported in a nationwide population-based study of more than 14,000 cases from 1987 to 2002. Circulation 2006, 114, 2611–2618. [Google Scholar] [CrossRef] [PubMed]
  2. Hagan, P.G.; Nienaber, C.A.; Isselbacher, E.M.; Bruckman, D.; Karavite, D.J.; Russman, P.L.; Evangelista, A.; Fattori, R.; Suzuki, T.; Oh, J.K.; et al. The International Registry of Acute Aortic Dissection (IRAD): New insights into an old disease. JAMA J. Am. Med. Assoc. 2000, 283, 897–903. [Google Scholar] [CrossRef]
  3. Roberts, C.S.; Roberts, W.C. Aortic dissection with the entrance tear in the descending thoracic aorta. Analysis of 40 necropsy patients. Ann. Surg. 1991, 213, 356–368. [Google Scholar] [CrossRef] [PubMed]
  4. Suzuki, T.; Mehta, R.H.; Ince, H.; Nagai, R.; Sakomura, Y.; Weber, F.; Sumiyoshi, T.; Bossone, E.; Trimarchi, S.; Cooper, J.V.; et al. Clinical profiles and outcomes of acute type B aortic dissection in the current era: Lessons from the International Registry of Aortic Dissection (IRAD). Circulation 2003, 108 (Suppl. 1), II312–II317. [Google Scholar] [CrossRef] [PubMed]
  5. Nienaber, C.A.; Fattori, R.; Lund, G.; Dieckmann, C.; Wolf, W.; von Kodolitsch, Y.; Nicolas, V.; Pierangeli, A. Nonsurgical reconstruction of thoracic aortic dissection by stent-graft placement. N. Engl. J. Med. 1999, 340, 1539–1545. [Google Scholar] [CrossRef] [PubMed]
  6. Dake, M.D.; Kato, N.; Mitchell, R.S.; Semba, C.P.; Razavi, M.K.; Shimono, T.; Hirano, T.; Takeda, K.; Yada, I.; Miller, D.C. Endovascular stent-graft placement for the treatment of acute aortic dissection. N. Engl. J. Med. 1999, 340, 1546–1552. [Google Scholar] [CrossRef] [PubMed]
  7. Herman, I.M.; Brant, A.M.; Warty, V.S.; Bonaccorso, J.; Klein, E.C.; Kormos, R.L.; Borovetz, H.S. Hemodynamics and the vascular endothelial cytoskeleton. J. Cell Biol. 1987, 105, 291–302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  8. Blanco, P.J.; Pivello, M.R.; Urquiza, S.A.; Feijoo, R.A. On the potentialities of 3D-1D coupled models in hemodynamics simulations. J. Biomech. 2009, 42, 919–930. [Google Scholar] [CrossRef] [PubMed]
  9. Polanczyk, A.; Podgorski, M.; Wozniak, T.; Stefanczyk, L.; Strzelecki, M. Computational Fluid Dynamics as an Engineering Tool for the Reconstruction of Hemodynamics after Carotid Artery Stenosis Operation: A Case Study. Medicina 2018, 54, 42. [Google Scholar] [CrossRef]
  10. Cheng, Z.; Tan, F.P.; Riga, C.V.; Bicknell, C.D.; Hamady, M.S.; Gibbs, R.G.; Wood, N.B.; Xu, X.Y. Analysis of flow patterns in a patient-specific aortic dissection model. J. Biomech. Eng. 2010, 132, 051007. [Google Scholar] [CrossRef] [PubMed]
  11. Polanczyk, A.; Strzelecki, M.; Wozniak, T.; Szubert, W.; Stefanczyk, L. 3D Blood Vessels Reconstruction Based on Segmented CT Data for Further Simulations of Hemodynamic in Human Artery Branches. Found. Comput. Decis. Sci. 2017, 42, 359–371. [Google Scholar] [CrossRef] [Green Version]
  12. Shahcheraghi, N.; Dwyer, H.A.; Cheer, A.Y.; Barakat, A.I.; Rutaganira, T. Unsteady and three-dimensional simulation of blood flow in the human aortic arch. J. Biomech. Eng. 2002, 124, 378–387. [Google Scholar] [CrossRef] [PubMed]
  13. Lam, S.K.; Fung, G.S.; Cheng, S.W.; Chow, K.W. A computational study on the biomechanical factors related to stent-graft models in the thoracic aorta. Med. Biol. Eng. Comput. 2008, 46, 1129–1138. [Google Scholar] [CrossRef] [PubMed]
  14. Tse, K.M.; Chiu, P.; Lee, H.P.; Ho, P. Investigation of hemodynamics in the development of dissecting aneurysm within patient-specific dissecting aneurismal aortas using computational fluid dynamics (CFD) simulations. J. Biomech. 2011, 44, 827–836. [Google Scholar] [CrossRef] [PubMed]
  15. Kizilova, N. Computational approach to optimal transport network construction in biomechanics. Lect. Notes Comput. Sci. 2004, 3044, 476–485. [Google Scholar]
  16. Amblard, A.; Berre, H.W.L.; Bou-Said, B.; Brunet, M. Analysis of type I endoleaks in a stented abdominal aortic aneurysm. Med. Eng. Phys. 2009, 31, 27–33. [Google Scholar] [CrossRef] [PubMed]
  17. Xenos, M.; Rambhia, S.H.; Alemu, Y.; Einav, S.; Labropoulos, N.; Tassiopoulos, A.; Ricotta, J.J.; Bluestein, D. Patient-Based Abdominal Aortic Aneurysm Rupture Risk Prediction with Fluid Structure Interaction Modeling. Ann. Biomed. Eng. 2010, 38, 3323–3337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  18. Auer, M.; Gasser, T.C. Reconstruction and finite element mesh generation of abdominal aortic aneurysms from computerized tomography angiography data with minimal user interactions. IEEE Trans. Med. Imaging 2010, 29, 1022–1028. [Google Scholar] [CrossRef] [PubMed]
  19. Polanczyk, A.; Klinger, M.; Nanobachvili, J.; Huk, I.; Neumayer, C. Artificial Circulatory Model for Analysis of Human and Artificial Vessels. Appl. Sci. 2018, 8, 1017. [Google Scholar] [CrossRef]
  20. Papathanasopoulou, P.; Zhao, S.; Kohler, U.; Robertson, M.B.; Long, Q.; Hoskins, P.; Xu, X.Y.; Marshall, I. MRI measurement of time-resolved wall shear stress vectors in a carotid bifurcation model, and comparison with CFD predictions. J. Magn. Reson. Imaging JMRI 2003, 17, 153–162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  21. Fillinger, M.F.; Greenberg, R.K.; McKinsey, J.F.; Chaikof, E.L.; Society for Vascular Surgery Ad Hoc Committee on TRS. Reporting standards for thoracic endovascular aortic repair (TEVAR). J. Vasc. Surg. 2010, 52, 1022–1033. [Google Scholar] [CrossRef] [PubMed]
  22. Polanczyk, A.; Podyma, M.; Trebinski, L.; Chrzastek, J.; Zbicinski, I.; Stefanczyk, L. A Novel Attempt to Standardize Results of CFD Simulations Basing on Spatial Configuration of Aortic Stent-Grafts. PLoS ONE 2016, 11, e0153332. [Google Scholar] [CrossRef] [PubMed]
  23. Polanczyk, A.; Wozniak, T.; Strzelecki, M.; Szubert, W.; Stefanczyk, L. Evaluating an algorithm for 3D reconstruction of blood vessels for further simulations of hemodynamic in human artery branches. IEEE Xplore Dig. Libr. 2016, 5, 103–107. [Google Scholar]
  24. Polańczyk, A.; Podyma, M.; Stefańczyk, L.; Zbiciński, I. Effects of stent-graft geometry and blood hematocrit on hemodynamic in Abdominal Aortic Aneurysm. Chem. Process Eng. 2012, 33, 53–62. [Google Scholar] [CrossRef]
  25. Polanczyk, A.; Piechota-Polanczyk, A.; Stefanczyk, L. A new approach for the pre-clinical optimization of a spatial configuration of bifurcated endovascular prosthesis placed in abdominal aortic aneurysms. PLoS ONE 2017, 12, e0182717. [Google Scholar] [CrossRef] [PubMed]
  26. Hoskins, P.R. Simulation and validation of arterial ultrasound imaging and blood flow. Ultrasound Med. Biol. 2008, 34, 693–717. [Google Scholar] [CrossRef] [PubMed]
  27. Polanczyk, A.; Podyma, M.; Stefanczyk, L.; Szubert, W.; Zbicinski, I. A 3D model of thrombus formation in a stent-graft after implantation in the abdominal aorta. J. Biomech. 2015, 48, 425–431. [Google Scholar] [CrossRef] [PubMed]
  28. Granata, A.; Fiorini, F.; Andrulli, S.; Logias, F.; Gallieni, M.; Romano, G.; Sicurezza, E.; Fiore, C.E. Doppler ultrasound and renal artery stenosis: An overview. J. Ultrasound 2009, 12, 133–143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  29. Cheng, Z.; Juli, C.; Wood, N.B.; Gibbs, R.G.; Xu, X.Y. Predicting flow in aortic dissection: Comparison of computational model with PC-MRI velocity measurements. Med. Eng. Phys. 2014, 36, 1176–1184. [Google Scholar] [CrossRef] [PubMed]
  30. Dillon-Murphy, D.; Noorani, A.; Nordsletten, D.; Figueroa, C.A. Multi-modality image-based computational analysis of haemodynamics in aortic dissection. Biomech. Model. Mechanobiol. 2016, 15, 857–876. [Google Scholar] [CrossRef] [PubMed]
  31. Yu, S.C.; Liu, W.; Wong, R.H.; Underwood, M.; Wang, D. The Potential of Computational Fluid Dynamics Simulation on Serial Monitoring of Hemodynamic Change in Type, B. Aortic Dissection. Cardiovasc. Interv. Radiol. 2016, 39, 1090–1098. [Google Scholar] [CrossRef] [PubMed]
  32. Hoshina, K.; Sho, E.; Sho, M.; Nakahashi, T.K.; Dalman, R.L. Wall shear stress and strain modulate experimental aneurysm cellularity. J. Vasc. Surg. 2003, 37, 1067–1074. [Google Scholar] [CrossRef]
  33. Rudenick, P.A.; Bijnens, B.H.; Garcia-Dorado, D.; Evangelista, A. An in vitro phantom study on the influence of tear size and configuration on the hemodynamics of the lumina in chronic type B. aortic dissections. J. Vasc. Surg. 2013, 57, 464–474. [Google Scholar] [CrossRef] [PubMed]
  34. Ben Ahmed, S.; Dillon-Murphy, D.; Figueroa, C.A. Computational Study of Anatomical Risk Factors in Idealized Models of Type, B. Aortic Dissection. Eur. J. Vasc. Endovasc. Surg. Off. J. Eur. Soc. Vasc. Surg. 2016, 52, 736–745. [Google Scholar] [CrossRef] [PubMed]
  35. Karmonik, C.; Partovi, S.; Muller-Eschner, M.; Bismuth, J.; Davies, M.G.; Shah, D.J.; Loebe, M.; Böckler, D.; Lumsden, A.B.; von Tengg-Kobligk, H. Longitudinal computational fluid dynamics study of aneurysmal dilatation in a chronic DeBakey type III aortic dissection. J. Vasc. Surg. 2012, 56, 260–263. [Google Scholar] [CrossRef] [PubMed]
  36. Georgakarakos, E.; Ioannou, C.V.; Kamarianakis, Y.; Papaharilaou, Y.; Kostas, T.; Manousaki, E.; Katsamouris, A.N. The role of geometric parameters in the prediction of abdominal aortic aneurysm wall stress. Eur. J. Vasc. Endovasc. Surg. Off. J. Eur. Soc. Vasc. Surg. 2010, 39, 42–48. [Google Scholar] [CrossRef] [PubMed]
  37. Doyle, B.J.; Callanan, A.; Burke, P.E.; Grace, P.A.; Walsh, M.T.; Vorp, D.A.; McGloughlin, T.M. Vessel asymmetry as an additional diagnostic tool in the assessment of abdominal aortic aneurysms. J. Vasc. Surg. 2009, 49, 443–454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  38. Duvernois, V.; Marsden, A.L.; Shadden, S.C. Lagrangian analysis of hemodynamics data from FSI simulation. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 445–461. [Google Scholar] [CrossRef] [PubMed]
  39. Xiang, J.; Tremmel, M.; Kolega, J.; Levy, E.I.; Natarajan, S.K.; Meng, H. Newtonian viscosity model could overestimate wall shear stress in intracranial aneurysm domes and underestimate rupture risk. J. Neurointerv. Surg. 2012, 4, 351–357. [Google Scholar] [CrossRef] [PubMed]
Applsci 08 01309 g001 550
Figure 1. Representative 3D reconstructions of the aorta and aortic branches before (Panel 1) and after (Panel 2) the thoracic endovascular aortic repair (TEVAR) procedure. CTA scans were used to reconstruct the aortic arch (A), the left renal artery (B), the right common iliac artery (C). Blue colour represents aorta, red colour represents aortic stent graft. Post—TEVAR refers to 7 months after operation. 3D reconstructions were performed with ANSYS FLUENT software.
Figure 1. Representative 3D reconstructions of the aorta and aortic branches before (Panel 1) and after (Panel 2) the thoracic endovascular aortic repair (TEVAR) procedure. CTA scans were used to reconstruct the aortic arch (A), the left renal artery (B), the right common iliac artery (C). Blue colour represents aorta, red colour represents aortic stent graft. Post—TEVAR refers to 7 months after operation. 3D reconstructions were performed with ANSYS FLUENT software.
Applsci 08 01309 g001
Applsci 08 01309 g002 550
Figure 2. Changes in blood velocity contours of the aortic arch for a representative patient. (top) velocity contour distribution in the aortic arch for representative time points before and 7 months after TEVAR; (bottom) the average velocity changes for one cardiac cycle. Changes in velocity contours were presented for the anterior and posterior position in the aortic arch. Numerical simulations were calculated using ANSYS FLUENT software.
Figure 2. Changes in blood velocity contours of the aortic arch for a representative patient. (top) velocity contour distribution in the aortic arch for representative time points before and 7 months after TEVAR; (bottom) the average velocity changes for one cardiac cycle. Changes in velocity contours were presented for the anterior and posterior position in the aortic arch. Numerical simulations were calculated using ANSYS FLUENT software.
Applsci 08 01309 g002
Applsci 08 01309 g003 550
Figure 3. Changes in blood velocity contours of the left renal artery for a representative patient. (top): velocity contour distribution in the left renal artery for representative time points before and 7 months after TEVAR; (bottom): the average velocity changes in the left renal artery for one cardiac cycle. Changes in velocity contours were presented for the anterior and posterior position in the left renal artery. Numerical simulations calculated using ANSYS FLUENT software.
Figure 3. Changes in blood velocity contours of the left renal artery for a representative patient. (top): velocity contour distribution in the left renal artery for representative time points before and 7 months after TEVAR; (bottom): the average velocity changes in the left renal artery for one cardiac cycle. Changes in velocity contours were presented for the anterior and posterior position in the left renal artery. Numerical simulations calculated using ANSYS FLUENT software.
Applsci 08 01309 g003
Applsci 08 01309 g004 550
Figure 4. Changes in wall shear stress (WSS) contour distribution in the thoracic aorta for a representative patient. (top): WSS contour distribution in the thoracic aorta for representative time points before and 7 months after TEVAR; (bottom): the average velocity changes in the thoracic aorta for one cardiac cycle. Changes in WSS contours were presented for the anterior and posterior position in the left renal artery. Numerical were simulations calculated using ANSYS FLUENT software.
Figure 4. Changes in wall shear stress (WSS) contour distribution in the thoracic aorta for a representative patient. (top): WSS contour distribution in the thoracic aorta for representative time points before and 7 months after TEVAR; (bottom): the average velocity changes in the thoracic aorta for one cardiac cycle. Changes in WSS contours were presented for the anterior and posterior position in the left renal artery. Numerical were simulations calculated using ANSYS FLUENT software.
Applsci 08 01309 g004
Applsci 08 01309 g005 550
Figure 5. Changes in WSS contour distribution in the left renal artery for a representative patient. (top): WSS contour distribution in the left renal artery for representative time points before and 7 months after TEVAR; (bottom): the average velocity changes in the left renal artery for one cardiac cycle. Changes in WSS contours are presented for the anterior and posterior position in the left renal artery. Numerical simulations were calculated in ANSYS FLUENT software.
Figure 5. Changes in WSS contour distribution in the left renal artery for a representative patient. (top): WSS contour distribution in the left renal artery for representative time points before and 7 months after TEVAR; (bottom): the average velocity changes in the left renal artery for one cardiac cycle. Changes in WSS contours are presented for the anterior and posterior position in the left renal artery. Numerical simulations were calculated in ANSYS FLUENT software.
Applsci 08 01309 g005
Table
Table 1. Spatial characterisation of analysed patients. Dissection and prosthesis placement according to Fillinger et al., 2010 [21].
Table 1. Spatial characterisation of analysed patients. Dissection and prosthesis placement according to Fillinger et al., 2010 [21].
NamePatient 1Patient 2Patient 3Patient 4Patient 5
Dissection TypeIIIbIIIbIIIbIIIbIIIb
Entry TearProximal to the left subclavian artery (LSA)
(zone number 4 according to Fillinger et al., 2010)
End of DissectionRight iliac artery (zone number 9 according to Fillinger et al., 2010)Right iliac artery (zone number 9 according to Fillinger et al., 2010)Right iliac artery (zone number 9 according to Fillinger et al., 2010)Left renal artery (zone number 8 according to Fillinger et al., 2010)Left renal artery (zone number 8 according to Fillinger et al., 2010)
Vascular ProsthesisOne stent-graft (115 mm) (zone number 3–4 according to Fillinger et al., 2010), two self-expanded stents (left renal artery (zone number 10 according to Fillinger et al., 2010) and right iliac artery (zone number 8 according to Fillinger et al., 2010)) (25 mm renal, 25 mm iliac)One stent-graft (117 mm) (zone number 3–4 according to Fillinger et al., 2010), two self-expanded stents (left renal artery (zone number 10 according to Fillinger et al., 2010) and right iliac artery (zone number 8 according to Fillinger et al., 2010)) (30 mm renal, 25 mm iliac)One stent-graft (118 mm) (zone number 3–4 according to Fillinger et al., 2010), two self-expanded stents (left renal artery (zone number 10 according to Fillinger et al., 2010) and right iliac artery (zone number 8 according to Fillinger et al., 2010)) (25 mm renal, 30 mm iliac)One stent-graft (120 mm) (zone number 3–4 according to Fillinger et al., 2010), one self-expanded stent (right iliac artery (zone number 8 according to Fillinger et al., 2010)) (27 mm renal)One stent-graft (120 mm) (zone number 3–4 according to Fillinger et al., 2010), one self-expanded stent (right iliac artery (zone number 8 according to Fillinger et al., 2010)) (30 mm renal)
Table
Table 2. Changes in blood flow [mL/s] for pre- and post- thoracic endovascular aortic repair (TEVAR) for ultrasonography (USG-Doppler) and computational fluid dynamics (CFD). Data are presented as the median (Q1;Q3). N = 5. p-values were calculated using the Wilcoxon Ranked Sign test.
Table 2. Changes in blood flow [mL/s] for pre- and post- thoracic endovascular aortic repair (TEVAR) for ultrasonography (USG-Doppler) and computational fluid dynamics (CFD). Data are presented as the median (Q1;Q3). N = 5. p-values were calculated using the Wilcoxon Ranked Sign test.
Artery TypeBlood Flow [mL/s]
USG-Doppler CFD
Pre-TEVAR
Median [Q1;Q2]		Post TEVAR
Median [Q1;Q2]		p ValuePre TEVAR
Median [Q1;Q2]		Post TEVAR
Median [Q1;Q2]		p Value
Thoracic trunk7.724
(7.089; 9.600)		65.220
(64.990; 65.300)		p = 0.0439.100
(9.100;9.100)		61.720
(61.700;63.050)		p = 0.043
Brachiocephalic trunk5.300
(4.810;5.920)		5.050
(4.370;5.200)		p = 0.0435.470
(4.760;5.848)		4.860
(4.760;5.280)		p = 0.273
Carotid arteries4.840
(4.500;5.360)		4.610
(4.230;5.100)		p = 0.0435.030
(4.470;5.320)		4.620
(4.470;5.070)		p = 0.715
Subclavian arteries4.290
(4.140;4.720)		4.170
(4.020;4.400)		p = 0.0434.250
(4.010;4.664)		4.110
(3.820;4.250)		p = 0.273
Renal arteries9.300
(8.870;9.430)		9.705
(9.500;9.925)		p = 0.0439.280
(9.175;9.472)		10.400
(9.885;10.495)		p = 0.043
Iliac arteries2.320
(2.135;2.377)		1.985
(1.912;2.050)		p = 0.0792.135
(2.045;2.135)		2.007
(1.947;2.047)		p = 0.079
Table
Table 3. Changes in blood velocity [m/s] pre- and post-TEVAR for USG-Doppler and CFD. Data are presented as the median (Q1;Q3). N = 5. p-values were calculated using the Wilcoxon Ranked Sign test.
Table 3. Changes in blood velocity [m/s] pre- and post-TEVAR for USG-Doppler and CFD. Data are presented as the median (Q1;Q3). N = 5. p-values were calculated using the Wilcoxon Ranked Sign test.
Artery TypeBlood Velocity [m/s]
USG-DopplerCFD
Pre TEVAR
Median [Q1;Q2]		Post TEVAR
Median [Q1;Q2]		p ValuePre TEVAR
Median [Q1;Q2]		Post TEVAR
Median [Q1;Q2]		p Value
Thoracic trunk0.273
(0.250;0.339)		0.223
(0.208;0.255)		p = 0.0430.321
(0.321;0.321)		0.217
(0.203;0.239)		p = 0.043
Renal arteries0.315
(0.306;0.328)		0.343
(0.335;0.351)		p = 0.0430.324
(0.317;0.328)		0.355
(0.349;0.371)		p = 0.043
Iliac arteries0.034
(0.034;0.035)		0.032
(0.031;0.034)		p = 0.0790.033
(0.032;0.035)		0.031
(0.031;0.031)		p = 0.079

Share and Cite

MDPI and ACS Style

Polanczyk, A.; Piechota-Polanczyk, A.; Domenig, C.; Nanobachvili, J.; Huk, I.; Neumayer, C. Computational Fluid Dynamic Accuracy in Mimicking Changes in Blood Hemodynamics in Patients with Acute Type IIIb Aortic Dissection Treated with TEVAR. Appl. Sci. 2018, 8, 1309. https://doi.org/10.3390/app8081309

AMA Style

Polanczyk A, Piechota-Polanczyk A, Domenig C, Nanobachvili J, Huk I, Neumayer C. Computational Fluid Dynamic Accuracy in Mimicking Changes in Blood Hemodynamics in Patients with Acute Type IIIb Aortic Dissection Treated with TEVAR. Applied Sciences. 2018; 8(8):1309. https://doi.org/10.3390/app8081309

Chicago/Turabian Style

Polanczyk, Andrzej, Aleksandra Piechota-Polanczyk, Christoph Domenig, Josif Nanobachvili, Ihor Huk, and Christoph Neumayer. 2018. "Computational Fluid Dynamic Accuracy in Mimicking Changes in Blood Hemodynamics in Patients with Acute Type IIIb Aortic Dissection Treated with TEVAR" Applied Sciences 8, no. 8: 1309. https://doi.org/10.3390/app8081309

APA Style

Polanczyk, A., Piechota-Polanczyk, A., Domenig, C., Nanobachvili, J., Huk, I., & Neumayer, C. (2018). Computational Fluid Dynamic Accuracy in Mimicking Changes in Blood Hemodynamics in Patients with Acute Type IIIb Aortic Dissection Treated with TEVAR. Applied Sciences, 8(8), 1309. https://doi.org/10.3390/app8081309

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop