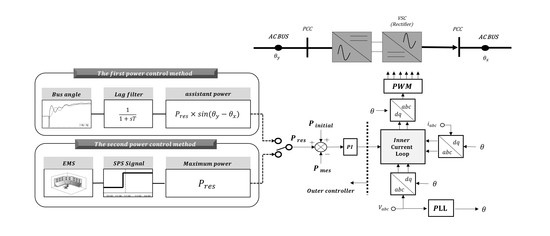
3.1. The First Power Control Model of BTB VSC
The process to obtain a first power control model with the bus monitoring system is explained in this section. The goal is to make BTB VSC act like an ac transmission when contingencies occur. It contributes to the improvement of transient stability, since it reacts like other ac transmission lines that find a new convergence point after a contingency. Therefore, the ac transmission characteristics have to be involved in the BTB VSC. In the ac grid, the transfer power is determined by each side of the angle difference that provides a clue to infer the condition of the ac system. The BTB VSCs equipped with each side of bus angle information can react differently depending on the ac grid condition. To apply the angle difference variation to an active power controller, below assumption is needed [
8]:
The power transfer equation is illustrated as the sending end voltage , receiving end voltage and line impedance between two buses, in which is the angle difference between the sending and receiving ends. With the ac voltage control, the converter constantly controls the ac voltage as 1.0 pu, and the voltage variation is assumed to be zero. The impedance that determines the amount of power is a constant value between ac grid and BTB VSC system. Finally, in the VSC, the power variation occurs when the angle difference between connected two buses is detected.
In the first power control method, the angle information of each side of ac buses are transferred through a first order lag filter, and the information used in the assistant power controller to emulate the ac transmission power flow characteristics as shown in
Figure 3. The filter is required for the measured signal to remove the initial overshoots, as well as any higher angle oscillations. The power reference changes when an angle variation is detected, and the reference is obtained as
in which
is a delay constant from the control lag, output limiter, and communication system. The
is initial dc power for the user-selected purpose in the steady-state condition. The
can be set for various reasons by grid operators, including the maximum power-voltage margin, improved power transmission capability, minimum power transfer cost, etc. Note that the sin function has a range of −1 to 1, the assistant power reference is always smaller than remaining active power of the converter as
. Thus, the
determines the range of the angle stability improvement.
There are two purposes for a set
value. First, the contingencies nearby the BTB VSC result in a high angle variation. This means that the assistant power reference could have large fluctuations in a small power system [
9]. This easily impacts the system stability in which grid inertia is low. Second, the unlimited power reference could impact the system margin, leading to an unstable eigenvalue mode of active power controller. Therefore, setting the
is reasonable.
In detail, for example, when the fault occurs right next to the
side of the BTB, the arbitrary bus angle at the
side is immediately increased, since nearby generators increase their rotor speed to supply active power. What we want to see is the first damping of the bus angle in a sequence of a contingency. From
Figure 3, the angle variation of the
side more sensitively increases rather than the opposite side of
. From (9), the bus angle makes
terms negative in transient time, and the
becomes negative as well. The total power output (
) is decreased to deliver more power to the
side. On the other hand, when the fault occurs right next to the
side of the BTB, bus angle at the
side is more increased than the other side in transient time. It makes
terms positive, and the total output power going to
side is increased. In conclusion, the bus angle information reflects the ac grid condition directly after the contingency, and more power flows from the converter to the ac grid with the first power control strategy can reduce the required decelerating energy.
The operation point of the active power is consistently changed due to varying angle differences such as ac transmission line; therefore, the grid operators should accurately determine the reserve active power as . The reason for using reserve power and not using initial power ( for the proposed power control is that it can easily make the reverse direction power flow from the angle measuring system. This involves a high variation in power change, and it can worsen the ac grid condition in some cases. Also, another object of the first method is to use the remaining converter capacity to increase the converter utilization. Thus, the first power control method contribution to the stability of the ac grid is naturally constrained by a limiter.
The specific determination process of reserve active power is illustrated hereafter. The
is calculated by the converter rating (S), required reactive power (
from a severe contingency, and the initial active power (
.
Since the ac voltage control of the embedded BTB VSC has the highest priority in the transient time, sufficient reserve capacity of the reactive power such as
is required. However, the reactive power injecting or absorbing the ac grid can be limited by key parameters such as the ac grid voltage, converter voltage, and ac grid equivalent impedance. The maximum reactive power the converter can absorb or inject to the ac grid is limited by the two well-known equations below [
10]. The reactive power is constrained by the (11) as the “critical frontier” is the relation between the transmitted active power and reactive power. Beyond the critical frontier area, the ac grid voltage becomes unstable and collapses.
in which
is the VSC reactive power;
is the ac grid voltage;
is the reactance between the VSC and the ac grid
Other equations such as (12) represent the capability of the VSC to inject the reactive power into the ac system. (12) formed circular is moved by the ac grid voltage and equivalent impedance.
in which
is the apparent power at the ac system node;
is the converter side voltage;
The allowable reactive power range is firstly calculated to determine the range of
. If the reactive power is not limited by the ac grid condition, the
is chosen based on the required amount when the three-phase fault occurs near the BTB VSC system. If the reactive power consumption to maintain the voltage of the weak ac grid is large, the converter following the tendency of the ac transmission characteristic is naturally limited. The detailed determination process is illustrated below in
Figure 4.
3.2. The Second Power Control Model of BTB VSC
Each country, whether it has a different Special Protection System (SPS), as the generators tripping schemes are generally called, commonly commands specific generators to be tripped to balance the grid power. This process is generally adopted by grid operators, and to prevent the fault spread, the SPS signal that commands each generator to be tripped is activated. Under an N-2 contingency, as the level of fault increases, more generator rejection has to be applied to sustain the grid stability. The common protocol of SPS is performed according to time domain simulation with major contingencies, and the stability margin is determined by the index of acceleration and the decelerating energy [
11,
12].
With the second power control strategy, the flexible operation of the generator tripping scheme can be achieved without significant decelerating energy as the generators trip. The BTB VSCs surely contributes to the stability of the ac grid using a simple converter control strategy that transfers the maximum power reserve instantly to the fault area. Note that the more VSCs equipped with a proposed power control scheme the flexible tripping schemes on the generators will be possible for grid operators.
Figure 5 represents the diagram of the second power control scheme. If the SPS signal is activated, the power reference with the second power control scheme is represented by
in which
is the delay time when the BTB VSC receives the SPS signal, and it is set by 5 cycles after the fault in this paper. The activating time is naturally faster than the generator tripping scheme as with 9 cycles, since mechanical switch is not included. The
F coordinated by the grid operators only impacts the direction of the active power reserve based on the fault position, and the
S1 and
S2 are the switch to separate the first power control and the second power control method. The initial value of
S2 is zero for the first method.
To verify the effectiveness of the second power control method, the Equal Area Criterion (EEAC) concept is introduced. From the well-established EEAC [
11,
12], the accelerating area is defined as
, and the decelerating area as
. To configure the stable system, the size between
and
has to be equal. The main cause of this improvement is that the proposed strategy can increase the height of the
area during contingency.
Figure 6 represents the power-angle curve and the decelerating area with and without the second power control strategy.
From [
11,
12], the rotor angle (
increases by increasing the mechanical output
or by reducing the electrical output
as in (14):
in which E is an internal voltage of the generator, and
and
are the reactance of an equivalent transformer reactance and reactance of the transmission lines, respectively. The relation between
and
with a generation tripping scheme can be represented by (16), and the common protocols of calculating the
area with the second power control scheme can be written as
in which
is the start time when the second power controller impacts the VSCs. If the BTB VSCs receive the SPS signal where a severe contingency occurs in the ac system, the corresponding
, which is the maximum reserve power, is used. With the proposed scheme, the loss of mechanical output generated by the tripping scheme is naturally smaller than (17). (18) verifies that the first damping angle of the equivalent generators could be reduced further than the non-applied proposed operation scheme. The main one prevents the rest from a potential loss of synchronisms where the proposed scheme is applied. Eventually, the second control strategy can reduce the number of generator units ordered by SPS.