Strain Control of the Tunable Physical Nature of a Newly Designed Quaternary Spintronic Heusler Compound ScFeRhP
Abstract
1. Introduction
2. Calculation Method
3. Results and Discussion
3.1. Structural Stability and Total Energy
3.2. Electronic Structure and Slater–Pauling Rule
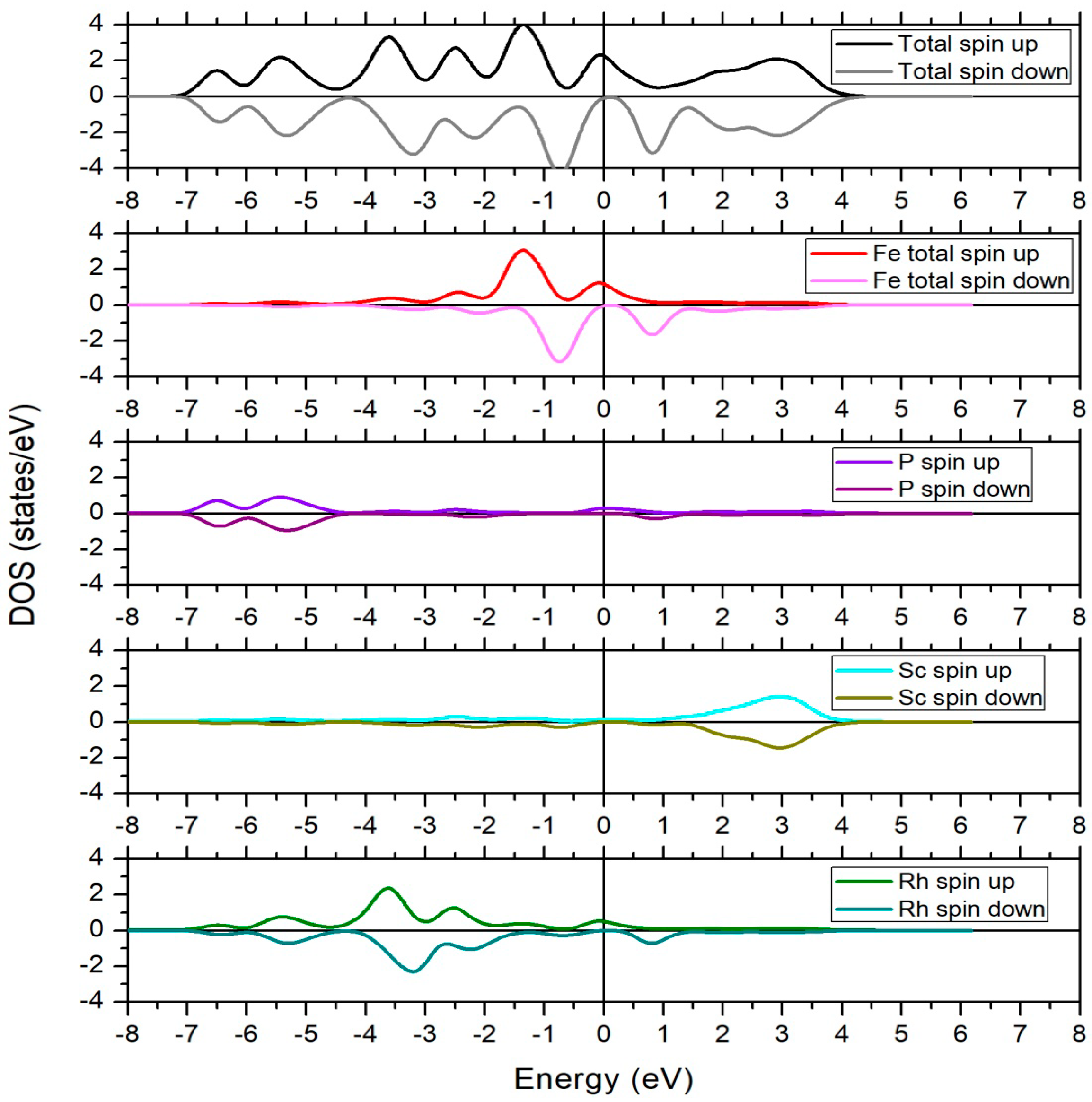
3.3. Magnetic Properties
3.4. Transitions of the Physical State under Uniform Strain
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Groot, R.A.D.; Mueller, F.M.; Engen, P.G.V.; Buschow, K.H.J. New class of materials: Half-metallic ferromagnets. Phys. Rev. Lett. 1983, 50, 2024–2027. [Google Scholar] [CrossRef]
- Wang, X.T.; Dai, X.F.; Wang, L.Y.; Liu, X.F.; Wang, W.H.; Wu, G.H.; Tang, C.C.; Liu, G.D. Electronic structures and magnetism of Rh3Z (Z = Al, Ga, In, Si, Ge, Sn, Pb, Sb) with DO3 structures. J. Magn. Magn. Mater. 2015, 378, 16–23. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Z.; Liu, G. Largest magnetic moments in the half-Heusler alloys XCrZ (X = Li, K, Rb, Cs; Z = S, Se, Te): A first-principles study. Materials 2017, 10, 1078. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Cheng, Z.; Wang, W. L21 and XA ordering competition in hafnium-based full-Heusler alloys Hf2VZ (Z = Al, Ga, In, Tl, Si, Ge, Sn, Pb). Materials 2017, 10, 1200. [Google Scholar] [CrossRef] [PubMed]
- Bainsla, L.; Suresh, K.G. Equiatomic quaternary Heusler alloys: A material perspective for spintronic applications. Appl. Phys. Rev. 2016, 3, 031101. [Google Scholar] [CrossRef]
- Han, Y.; Wu, Y.; Li, T.; Khenata, R.; Yang, T.; Wang, X. Electronic, magnetic, half-metallic, and mechanical properties of a new equiatomic quaternary Heusler compound YRhTiGe: A first-principles study. Materials 2018, 11, 797. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.L. Proposal for a new class of materials: Spin gapless semiconductors. Phys. Rev. Lett. 2008, 100, 156404. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Cheng, Z.; Liu, G.; Dai, X.; Khenata, R.; Wang, L.; Bouhemadou, A. Rare earth-based quaternary Heusler compounds MCoVZ (M = Lu, Y; Z = Si, Ge) with tunable band characteristics for potential spintronic applications. IUCrJ 2017, 4, 758–768. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, X.; Cheng, Z. Electronic, magnetic, mechanical, half-metallic and highly dispersive zero-gap half-metallic properties of rare-earth-element-based quaternary Heusler compounds. J. Alloys Compd. 2017, 718, 63–74. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.; Probert, M.A.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. 2002, 14, 2717. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Maximoff, S.N.; Ernzerhof, M.; Scuseria, G.E. Current-dependent extension of the Perdew-Burke-Ernzerhof exchange-correlation functional. J. Chem. Phys. 2004, 120, 2105–2109. [Google Scholar] [CrossRef] [PubMed]
- Ozdogan, K.; Sasıoglu, E.; Galanakis, I. Slater-Pauling behavior in LiMgPdSn-type multifunctional quaternary Heusler materials: Half-metallicity, spin-gapless and magnetic semiconductors. J. Appl. Phys. 2013, 113, 193903. [Google Scholar] [CrossRef]
- Galanakis, I.; Dederichs, P.H.; Papanikolaou, N. Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 2002, 66, 174429. [Google Scholar] [CrossRef]
- Galanakis, I.; Mavropoulos, P.; Dederichs, P.H. Electronic structure and Slater-Pauling behaviour in half-metallic Heusler alloys calculated from first principles. J. Phys. D Appl. Phys. 2006, 39, 765. [Google Scholar] [CrossRef]








| Type | P | Fe | Sc | Rh |
|---|---|---|---|---|
| Type 1 | A (0, 0, 0) | B (1/4, 1/4, 1/4) | C (1/2, 1/2, 1/2) | D (3/4, 3/4, 3/4) |
| Type 2 | A (0, 0, 0) | C (1/2, 1/2, 1/2) | B (1/4, 1/4, 1/4) | D (3/4, 3/4, 3/4) |
| Type 3 | B (1/4, 1/4, 1/4) | A (0, 0, 0) | C (1/2, 1/2, 1/2) | D (3/4, 3/4, 3/4) |
| States | Calculated Value | Type 1 | Type 2 | Type 3 |
|---|---|---|---|---|
| FM | Equilibrium lattice constant | 5.97 Å | 6.14 Å | 6.18 Å |
| Total energy | −2931.40 eV | −2930.75 eV | −2930.72 eV | |
| NM | Equilibrium lattice constant | 5.96 Å | 6.08 Å | 6.10 Å |
| Total energy | −2931.23 eV | −2929.80 eV | −2930.06 eV |
| Compound | Total | P | Fe | Sc | Rh | a (Å) | Zt | S-P Rule |
|---|---|---|---|---|---|---|---|---|
| ScFeRhP | 1.00 | 0.04 | 0.98 | −0.24 | 0.22 | 5.97 | 25 | Mt = Zt − 24 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Rozale, H.; Gao, Y.; Xu, H. Strain Control of the Tunable Physical Nature of a Newly Designed Quaternary Spintronic Heusler Compound ScFeRhP. Appl. Sci. 2018, 8, 1581. https://doi.org/10.3390/app8091581
Chen Z, Rozale H, Gao Y, Xu H. Strain Control of the Tunable Physical Nature of a Newly Designed Quaternary Spintronic Heusler Compound ScFeRhP. Applied Sciences. 2018; 8(9):1581. https://doi.org/10.3390/app8091581
Chicago/Turabian StyleChen, Zongbin, Habib Rozale, Yongchun Gao, and Heju Xu. 2018. "Strain Control of the Tunable Physical Nature of a Newly Designed Quaternary Spintronic Heusler Compound ScFeRhP" Applied Sciences 8, no. 9: 1581. https://doi.org/10.3390/app8091581
APA StyleChen, Z., Rozale, H., Gao, Y., & Xu, H. (2018). Strain Control of the Tunable Physical Nature of a Newly Designed Quaternary Spintronic Heusler Compound ScFeRhP. Applied Sciences, 8(9), 1581. https://doi.org/10.3390/app8091581




