Fine-Grain Segmentation of the Intervertebral Discs from MR Spine Images Using Deep Convolutional Neural Networks: BSU-Net
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
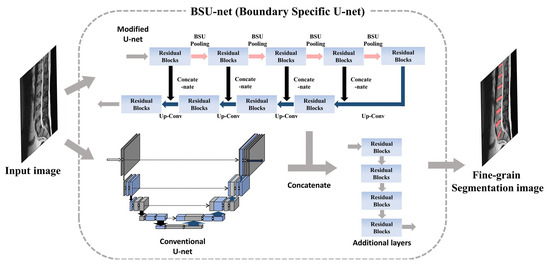
2.1. Network Design: Boundary Specific U-Network (BSU-Net)
2.1.1. BSU-Pooling Layer
2.1.2. Residual Block
2.1.3. Cascaded Network
2.2. Experimental Materials
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Luoma, K.; Riihimäki, H.; Luukkonen, R.; Raininko, R.; Viikari-Juntura, E.; Lamminen, A. Low back pain in relation to lumbar disc degeneration. Spine 2000, 25, 487–492. [Google Scholar] [CrossRef] [PubMed]
- Modic, M.T.; Steinberg, P.M.; Ross, J.S.; Masaryk, T.J.; Carter, J.R. Degenerative disk disease: Assessment of changes in vertebral body marrow with MR imaging. Radiology 1988, 166, 193–199. [Google Scholar] [CrossRef] [PubMed]
- Ayed, I.B.; Punithakumar, K.; Garvin, G.; Romano, W.; Li, S. Graph cuts with invariant object-interaction priors: Application to intervertebral disc segmentation. In Proceedings of the Biennial International Conference on Information Processing in Medical Imaging, Kloster Irsee, Germany, 3–8 July 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 221–232. [Google Scholar]
- Michopoulou, S.K.; Costaridou, L.; Panagiotopoulos, E.; Speller, R.; Panayiotakis, G.; Todd-Pokropek, A. Atlas-based segmentation of degenerated lumbar intervertebral discs from MR images of the spine. IEEE Trans. Biomed. Eng. 2009, 56, 2225–2231. [Google Scholar] [CrossRef] [PubMed]
- Law, M.W.; Tay, K.; Leung, A.; Garvin, G.J.; Li, S. Intervertebral disc segmentation in MR images using anisotropic oriented flux. Med. Image Anal 2013, 17, 43–61. [Google Scholar] [CrossRef] [PubMed]
- Haq, R.; Besachio, D.A.; Borgie, R.C.; Audette, M.A. Using shape-aware models for lumbar spine intervertebral disc segmentation. In Proceedings of the 22nd International Conference on Pattern Recognition (ICPR), Stockholm, Sweden, 24–28 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3191–3196. [Google Scholar]
- Mansour, R.F. Deep-learning-based automatic computer-aided diagnosis system for diabetic retinopathy. Biomed. Eng. Lett. 2018, 8, 41–57. [Google Scholar] [CrossRef]
- Ji, X.; Zheng, G.; Belavy, D.; Ni, D. Automated intervertebral disc segmentation using deep convolutional neural networks. In Proceedings of the International Workshop on Computational Methods and Clinical Applications for Spine Imaging, Athens, Greece, 17 October 2016; Springer: Cham, Switzerland, 2016; pp. 38–48. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Ye, J.C.; Han, Y.; Cha, E. Deep convolutional framelets: A general deep learning framework for inverse problems. SIAM J. Imaging Sci. 2018, 11, 991–1048. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv, 2015; arXiv:1511.07122. [Google Scholar]
- Kim, S.; Bae, W.C.; Hwang, D. Automatic delicate segmentation of the intervertebral discs from MR spine images using deep convolutional neural networks: ICU-net. In Proceedings of the 26th Annual Meeting of ISMRM, Paris, France, 16–21 June 2018; p. 5401. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Qin, H.; Yan, J.; Li, X.; Hu, X. Joint training of cascaded CNN for face detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 3456–3465. [Google Scholar]
- Eo, T.; Jun, Y.; Kim, T.; Jang, J.; Lee, H.J.; Hwang, D. KIKI-net: Cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images. Magn. Reson. Med. 2018. [Google Scholar] [CrossRef] [PubMed]
- Christ, P.F.; Elshaer, M.E.A.; Ettlinger, F.; Tatavarty, S.; Bickel, M.; Bilic, P.; Rempfler, M.; Armbruster, M.; Hofmann, F.; D’Anastasi, M.; et al. Automatic liver and lesion segmentation in CT using cascaded fully convolutional neural networks and 3D conditional random fields. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; Springer: Cham, Switzerland, 2016; pp. 415–423. [Google Scholar]
- Liu, M.; Zhang, D.; Shen, D. Alzheimer’s Disease Neuroimaging Initiative. Ensemble sparse classification of Alzheimer’s disease. NeuroImage 2012, 60, 1106–1116. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.; Tao, X.; Li, R.; Ma, Z.; Jia, J. Video super-resolution via deep draft-ensemble learning. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 531–539. [Google Scholar]
- Deng, L.; Platt, J.C. Ensemble deep learning for speech recognition. In Proceedings of the Fifteenth Annual Conference of the International Speech Communication Association, Singapore, 14–18 September 2014; pp. 1915–1919. [Google Scholar]
- Cai, Y.; Osman, S.; Sharma, M.; Landis, M.; Li, S. Multi-modality vertebra recognition in arbitrary views using 3d deformable hierarchical model. IEEE Trans. Med. Imaging 2015, 34, 1676–1693. [Google Scholar] [CrossRef] [PubMed]
- Spineweb. Available online: http://spineweb.digitalimaginggroup.ca/ (accessed on 13 September 2018).
- Dubuisson, M.P.; Jain, A.K. A modified Hausdorff distance for object matching. In Proceedings of the 12th International Conference on Pattern Recognition, Jerusalem, Israel, 9–13 October 1994; IEEE: Piscataway, NJ, USA, 1994; pp. 566–568. [Google Scholar]
- McDonald, J.H. Handbook of Biological Statistics, 2nd ed.; Sparky House: Baltimore, MD, USA, 2009; Volume 2, pp. 173–181. [Google Scholar]
- TensorFlow. Available online: http://www.tensorflow.org/ (accessed on 13 September 2018).
- Yu, L.; Yang, X.; Chen, H.; Qin, J.; Heng, P.A. Volumetric ConvNets with Mixed Residual Connections for Automated Prostate Segmentation from 3D MR Images. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 66–72. [Google Scholar]
- Christ, P.F.; Ettlinger, F.; Grün, F.; Elshaera, M.E.A.; Lipkova, J.; Schlecht, S.; Ahmaddy, F.; Tatavarty, S.; Bickel, M.; Bilic, P.; et al. Automatic liver and tumor segmentation of CT and MRI volumes using cascaded fully convolutional neural networks. arXiv, 2017; arXiv:1702.05970. [Google Scholar]
- Yuan, Y.; Chao, M.; Lo, Y.C. Automatic skin lesion segmentation using deep fully convolutional networks with jaccard distance. IEEE Trans. Med. Imaging 2017, 36, 1876–1886. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, G.L.; Burgard, W.; Brox, T. Efficient deep models for monocular road segmentation. In Intelligent Robots and Systems (IROS), Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 4885–4891. [Google Scholar]
- Claudia, C.; Farida, C.; Guy, G.; Marie-Claude, M.; Carl-Eric, A. Quantitative evaluation of an automatic segmentation method for 3D reconstruction of intervertebral scoliotic disks from MR images. BMC Med. Imaging 2012, 12, 26. [Google Scholar] [CrossRef] [PubMed]










| Mean (%) | SD (%) | ||
|---|---|---|---|
| Whole area segmentation | U-net | 86.44 | 2.24 |
| Dilated U-net | 88.46 | 2.63 | |
| BSU-net | 89.44 | 2.14 | |
| Boundary segmentation (thickness = 1 pixel) | U-net | 44.16 | 4.18 |
| Dilated U-net | 52.45 | 4.08 | |
| BSU-net | 54.62 | 4.59 | |
| Boundary segmentation (thickness = 2 pixels) | U-net | 67.51 | 3.59 |
| Dilated U-net | 73.17 | 3.70 | |
| BSU-net | 74.85 | 3.20 |
| Mean (mm) | SD (mm) | |
|---|---|---|
| U-net | 0.89 | 0.14 |
| Dilated U-net | 0.86 | 0.14 |
| BSU-net | 0.81 | 0.10 |
| DSC (%) | MHD (mm) | |||
|---|---|---|---|---|
| Measurement 1 | Measurement 2 | Measurement 3 | ||
| Conventional U-net | 86.442.24 | 44.164.18 | 67.513.59 | 0.890.14 |
| U-net + BSU-pooling layer | 87.303.16 | 50.68 | 71.684.76 | 0.880.14 |
| U-net + BSU-layer | 87.192.67 | 51.885.67 | 71.685.48 | 0.900.18 |
| Cascaded U-net | 87.704.00 | 50.25 | 71.337.63 | 0.860.17 |
| BSU-net | 89.442.14 | 54.624.59 | 74.853.20 | 0.810.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Bae, W.C.; Masuda, K.; Chung, C.B.; Hwang, D. Fine-Grain Segmentation of the Intervertebral Discs from MR Spine Images Using Deep Convolutional Neural Networks: BSU-Net. Appl. Sci. 2018, 8, 1656. https://doi.org/10.3390/app8091656
Kim S, Bae WC, Masuda K, Chung CB, Hwang D. Fine-Grain Segmentation of the Intervertebral Discs from MR Spine Images Using Deep Convolutional Neural Networks: BSU-Net. Applied Sciences. 2018; 8(9):1656. https://doi.org/10.3390/app8091656
Chicago/Turabian StyleKim, Sewon, Won C. Bae, Koichi Masuda, Christine B. Chung, and Dosik Hwang. 2018. "Fine-Grain Segmentation of the Intervertebral Discs from MR Spine Images Using Deep Convolutional Neural Networks: BSU-Net" Applied Sciences 8, no. 9: 1656. https://doi.org/10.3390/app8091656
APA StyleKim, S., Bae, W. C., Masuda, K., Chung, C. B., & Hwang, D. (2018). Fine-Grain Segmentation of the Intervertebral Discs from MR Spine Images Using Deep Convolutional Neural Networks: BSU-Net. Applied Sciences, 8(9), 1656. https://doi.org/10.3390/app8091656