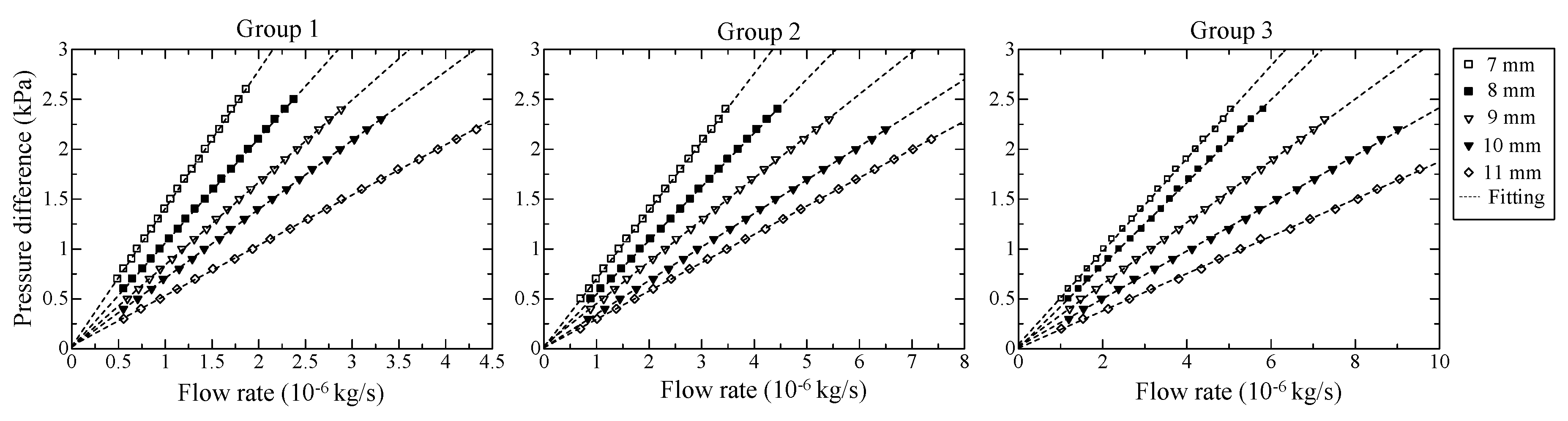Abstract
Sintered metal porous media are widely used in a broad range of industrial equipment. Generally, the flow properties in porous media are represented by an incompressible Darcy‒Forchheimer regime. This study uses a modified Forchheimer equation to represent the flow rate characteristics, which are then experimentally and theoretically investigated using a few samples of sintered metal porous media. The traditional steady-state method has a long testing time and considerable air consumption. With this in mind, a discharge method based on an isothermal chamber filled with copper wires is proposed to simultaneously determine the permeability and inertial coefficient. The flow rate discharged from the isothermal chamber is calculated by differentiating the measured pressure, and a paired dataset of pressure difference and flow rate is available. The theoretical representations of pressure difference versus flow rate show good agreement with the steady-state results. Finally, the volume limit of the isothermal chamber is addressed to ensure sufficient accuracy.
1. Introduction
Air flow through porous media is universal in a broad range of engineering activity, which includes such diverse fields as pneumatics, filtration, soil mechanics, and petroleum engineering. Pressure drops occur when such porous media are connected in an air circuit because they involve extremely complicated flow channels. Thus, accurate prediction of the correlation of pressure drop with flow rate is crucial for performance evaluation, since it determines the energy requirements of the supplying compressors. Some researchers have demonstrated the physics of flow through porous media. They modeled the flow behavior by a linear relation of pressure gradient versus flow velocity (Darcy regime) in cases where the flow is dominated by viscous effects. When the flow velocity becomes adequately large, they used a nonlinear relation to include the inertial effects [1,2,3,4,5,6].
Some researchers attempt to use theoretical methods to correlate with experimental data. The two best-known theoretical relations are the Forchheimer equation [7,8] and Ergun or Ergun-type equations [9,10]. Both are widely used [8], and there is no specific reason for choosing one rather than the other. Early works by Beavers et al. [11,12] reported that the flow pressure characteristics of porous media can be represented by a dimensionless expression related to the square root of the permeability. Montillet et al. [13] extended the applicability of an existing correlating equation to predict the pressure drop through packed beds of spheres. Antohe et al. [14] proposed a more precise method based on curve fitting to calculate the permeability and inertia coefficient of porous matrices in terms of a Forchheimer flow model. Dukhan and Minjeur [15] found that the permeability for the Darcy regime differs from that for the Forchheimer regime. Liu [16] developed an Ergun-type empirical equation to correlate the dimensionless pressure drop with flow velocity for several types of foam matrix porous media. Dukhan and Patel [17] correlated the permeability and the form drag coefficient using an Ergun model with the reciprocal of the surface area density, which has a unit of m3/m2, indicating that it is used as an equivalent length scale. Dietrich et al. [18] presented experimental data of pressure drop measurements of different ceramic sponges and determined the two constants of the Ergun equation, which are verified to be independent of the material and porosity. The Forchheimer and Ergun equations look very similar in that they both have a viscous term and an inertia term. The difference is that the Forchheimer equation uses an analogy with pipe flow while the Ergun equation models the space between packed beds of spheres as parallel capillaries. An overview of the literatures is provided in Table 1.

Table 1.
Classification of the references.
Air compressibility is negligible and flow velocity can be treated as a constant through porous media with a large porosity (over 0.8) [19,20,21]. Existing studies [22,23,24,25,26,27] proved that the Darcy‒Forchheimer-based theory can be applied to both compressible and incompressible fluids. Belforte et al. [22,23] measured considerable pressure differences during the operation of compressed air bearings equipped with sintered bronze porous pads. Nicoletti et al. [24] predicted the pressure‒flow relationship of the aerostatic porous bearing based on the quadratic Forchheimer assumption. Amano et al. [25], Oiwa et al. [26], and Miyatake et al. [27] have developed air conveyor systems with porous air supply pads. In these applications, the pressure drop is significant (400 kPa or more) and the air compressibility needs to be considered.
The authors have developed theoretical equations and represented the pressure drop characteristic of sintered metal porous media in terms of experimentally determined property coefficients [28,29,30,31]. However, the measurements are conducted under steady flow condition and this inevitably lengthens the test time and consumes much energy. Kawashima et al. [32] proposed a method using an isothermal chamber to obtain the flow rate characteristics of solenoid valves by the ISO 6358 equation. The equation depicts the flow rate characteristics with two independent parameters: sonic conductance C and critical pressure ratio b, which is determined in the choked flow state and subsonic flow state, respectively (the equation is detailed in the Appendix). The isothermal chamber is stuffed with steel or copper wool to enlarge the heat transfer area so that the air state change can be considered isothermal. Therefore, instantaneous flow rate charged into or discharged from the chamber can be indirectly calculated by differentiating the pressure in the chamber. If this approach can be applied to the test of porous media, the property coefficients can be ascertained more conveniently and effectively. To date, the discharge method has been used by other researchers for determining the flow rate characteristics of some pneumatic components (valves, etc.) in terms of the ISO 6358 equation. However, the porous media have very different properties to the common pneumatic components, and therefore the operating procedure needs to be reconstructed to extend its application to porous media. In this study, air is employed as the working fluid in order to investigate the flow rate characteristics of the porous media for some pneumatic applications (e.g., air bearing). The objective of the study is to use a simple and convenient method to measure and evaluate the permeability and inertial coefficient to represent the flow rate characteristics. Accordingly, a discharge method based on an isothermal chamber is proposed to conveniently ascertain the coefficients. This method accomplishes the test within the discharge process (only a few seconds), and of course reduces the air consumption. Three groups of sintered metal porous media made by different class of powder were tested. The validity of the discharge method was verified because the flow rate characteristics can be well represented with the determined coefficients.
2. Materials and Methods
For flowing through porous media with high enough velocity, the pressure gradient dP/dx versus flow velocity is described using the Forchheimer equation:
where μ is the air viscosity, v is the velocity, ρ is the density, K is the permeability and β is the inertial coefficient. The Forchheimer equation includes two terms denoting the viscous effect and the inertial effect. Removing the quadratic term yields the Darcy equation. The Forchheimer equation employs the square root of permeability as equivalent length characteristics in order to agree with the linear Darcy law at low velocities, and the dimensionless coefficient in the quadratic term is used to represent the inertial effect.
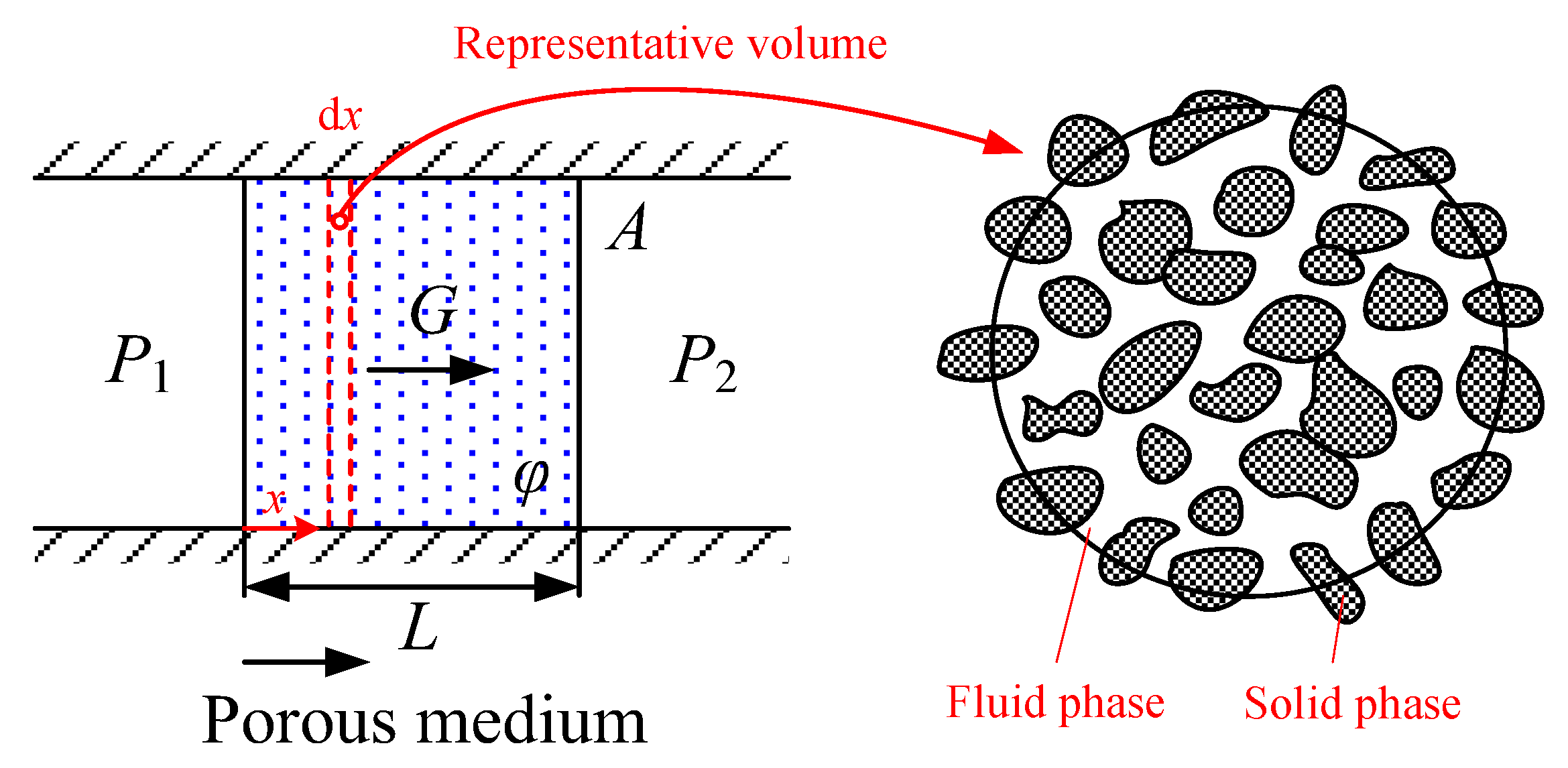
Figure 1 schematically shows the physical model for air flow through a porous medium. The flow is assumed to be steady and fully developed, and only in the length direction (x coordinate). Actually, the distribution of pores with respect to shape and size is irregular in the porous medium. On the microscopic scale, the flow quantities (velocity, pressure, etc.) are also clearly irregular. The Forchheimer regime models the flow through a porous medium as a pipe flow, and therefore the quantities of interest are described using the space-averaged quantities for representative areas that cross many pores. That is, as shown in Figure 1, the pressure and velocity are considered to be uniformly distributed along a tiny length (dx). Moreover, the porous medium is considered isotropic and homogeneous, and therefore the ratio of the circulation area and the total area equals the porosity.
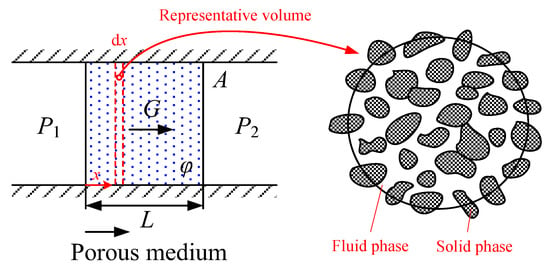
Figure 1.
Schematic diagram of airflow through a porous medium.
Accordingly, the mean flow velocity in each thin section (dx) varies with the air density, and can be calculated by the following expression:
where G is the mass flow rate, A is the cross-sectional area, and φ is the porosity.
According to the ideal gas state equation, the air density ρ can be expressed as below:
where R is the gas constant and T is the temperature.
Substituting Equations (2) and (3) into Equation (1) and integrating the pressure with respect to length (x-coordinate), with the boundary conditions P = P1 (x = 0 [m]), P = P2 (x = L [m]), weobtain the following modified Forchheimer equation:
The square root of the permeability is employed as a characteristic dimension and a Reynolds number is defined as
A dimensionless friction factor f is defined as
Comparing Equation (6) with the Darcy–Weisbach equation for the case of flowing in a cylindrical pipe, it is observed that the square root of permeability is actually equivalent to two times the hydraulic diameter of the pipe. Substituting Equations (5) and (6) into Equation (1) obtains the following correlation for the friction factor as a function of the Reynolds number:
3. Results
3.1. Test Medium
The porous media used were fabricated by sintering SUS316L powder at a temperature above 1000 °C. Three pieces of porous pad (Figure 2a), with a diameter of 40 mm and a length of 3 mm, were firstly made with existing models using different classes of powder to form different pore sizes. However, a large size not only compounds the difficulty in sealing but also requires a flow meter with a large measurement range. Hence, each original medium is cut into five small pieces to form a group (a total of three groups) to perform the experiments separately. Some studies [33,34] revealed that the size effect would influence the property coefficients. In this regard, as shown in Figure 2b, small pieces of samples are selected with a diameter of 7, 8, 9, 10, and 11 mm, which can be regarded as infinitely large compared with the pore size so that the wall effect in the porous media is negligible.

Figure 2.
Photographs of the porous medium: (a) Original porous media; (b) test porous media.
During the manufacturing process, particle size changes as a result of the shrinkage caused by the process’s linking effect. Therefore, we use SEM imaging (JEOL, Japan, JSM-6480) to roughly estimate the particle diameter for indication of the pore size. Three specimens for SEM testing are extracted at random from each group and the SEM photographs are shown in Figure 3. The particle diameters for the three groups of porous media are visually discernible in the figure, approximately in the range of 40–50 μm, 55–65 μm, and 80–90 μm, respectively. Regarding the porosity φ in the theoretical equations, it can be defined as the ratio of void space to the total volume and calculated as below:
where γ is the metal density (8.03 × 103 kg/m3), m is the mass of the medium, and V is the total volume. Table 2 lists the estimated particle diameter, dimensions, and porosity of the test porous media.

Figure 3.
SEM images of magnified particles for some porous media.

Table 2.
Properties of the test porous media in this study.
3.2. Steady-State Method
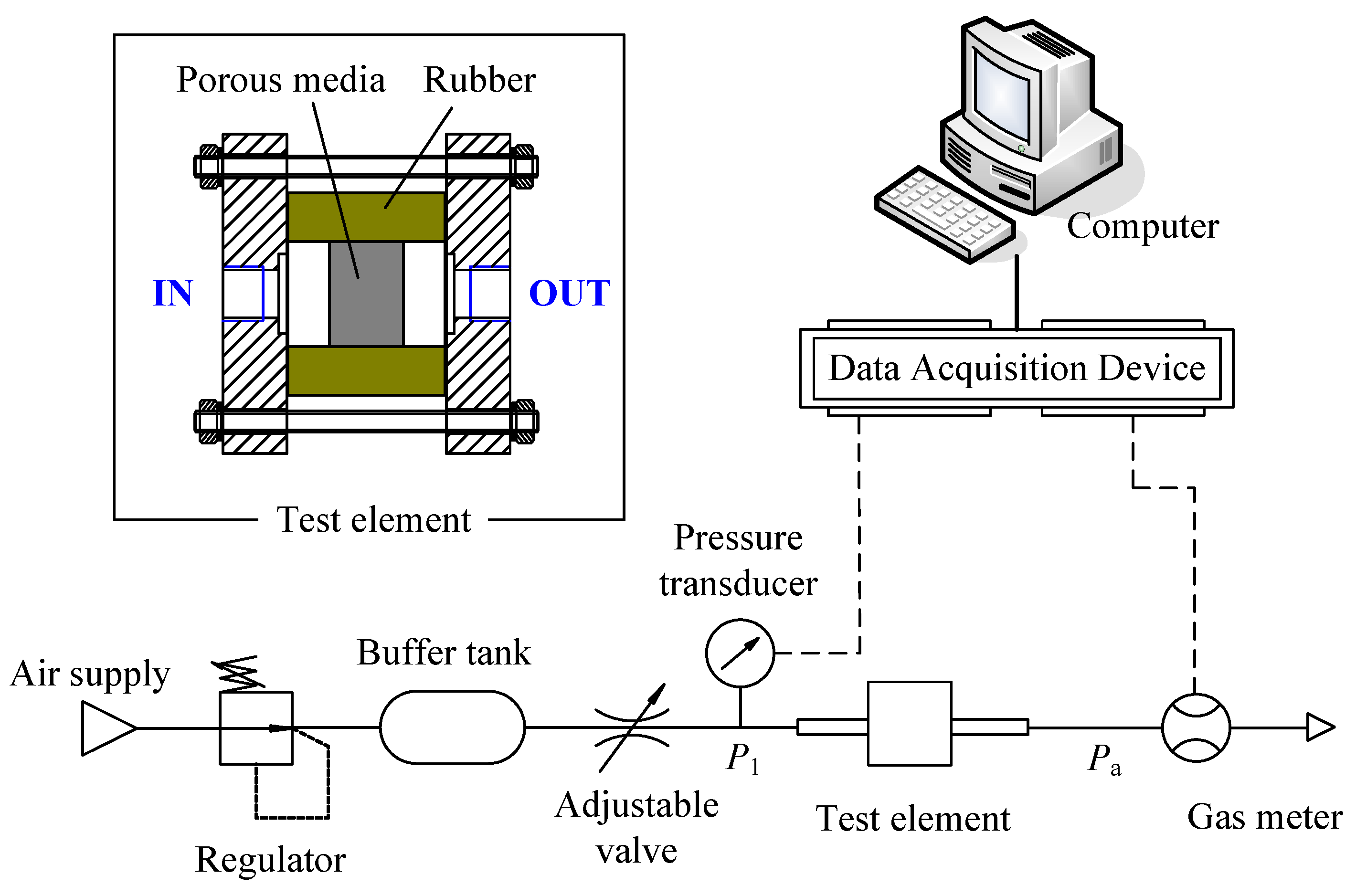
Figure 4 shows the pneumatic circuit for the measurement. Akbarnejad et al. [35] stated that if the test medium is not well sealed the measured parameters deviates greatly from its real value. In this work, the porous medium is placed in a cylindrical rubber and two end covers are used to compress the rubber. The rubber has a trend of reduction in the inner diameter when subjected to the axial compressing force. If the rubber is compressed tightly enough, the test medium can be well sealed. Pressurized air is adjusted by a regulator and a buffer tank with a volume of 10 L is in use. A pressure sensor (GE Druck, UK, PTX5012, range: 0–1 MPa, accuracy: 0.1%), which is carefully calibrated by a high-precision pressure controller (GE Druck, UK, PACE6000), is used to measure the upstream pressure, and the downstream pressure is treated as atmospheric pressure throughout. The pressure sensor is installed at a sufficient distance from the test element to eliminate the entrance effects. An adjustable valve is installed after the buffer tank to vary the flow rate. The flow rate in the circuit is measured by a dry test gas meter (DS-6A, Shinagawa Co., Ltd., Japan, range: 0.04~6 m3/h, accuracy: 0.3%). During the experiments, the paired data of pressure difference and flow rate are recorded as the opening of the valve is adjusted. For minute flow rate, a wet-type gas meter (W-NKDa-0.5A, Shinagawa Co., Ltd., Japan, range: 0.016‒5 L/min, accuracy: 0.1%) is used, and, correspondingly, the pressure difference is measured by a differential pressure transducer (PA-100-500D-S, Copal Co., Ltd, Japan, range: 0–5 kPa, accuracy: 0.5%).
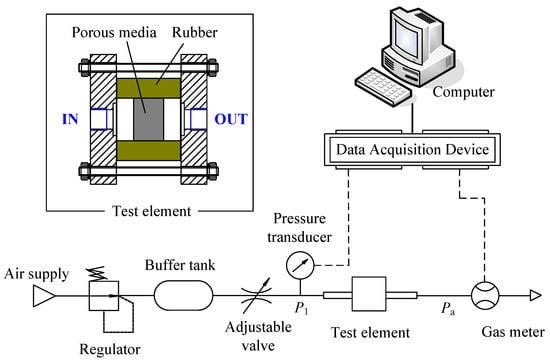
Figure 4.
Schematic of the apparatus for steady-state method.
3.3. Discharge Method with an Isothermal Chamber
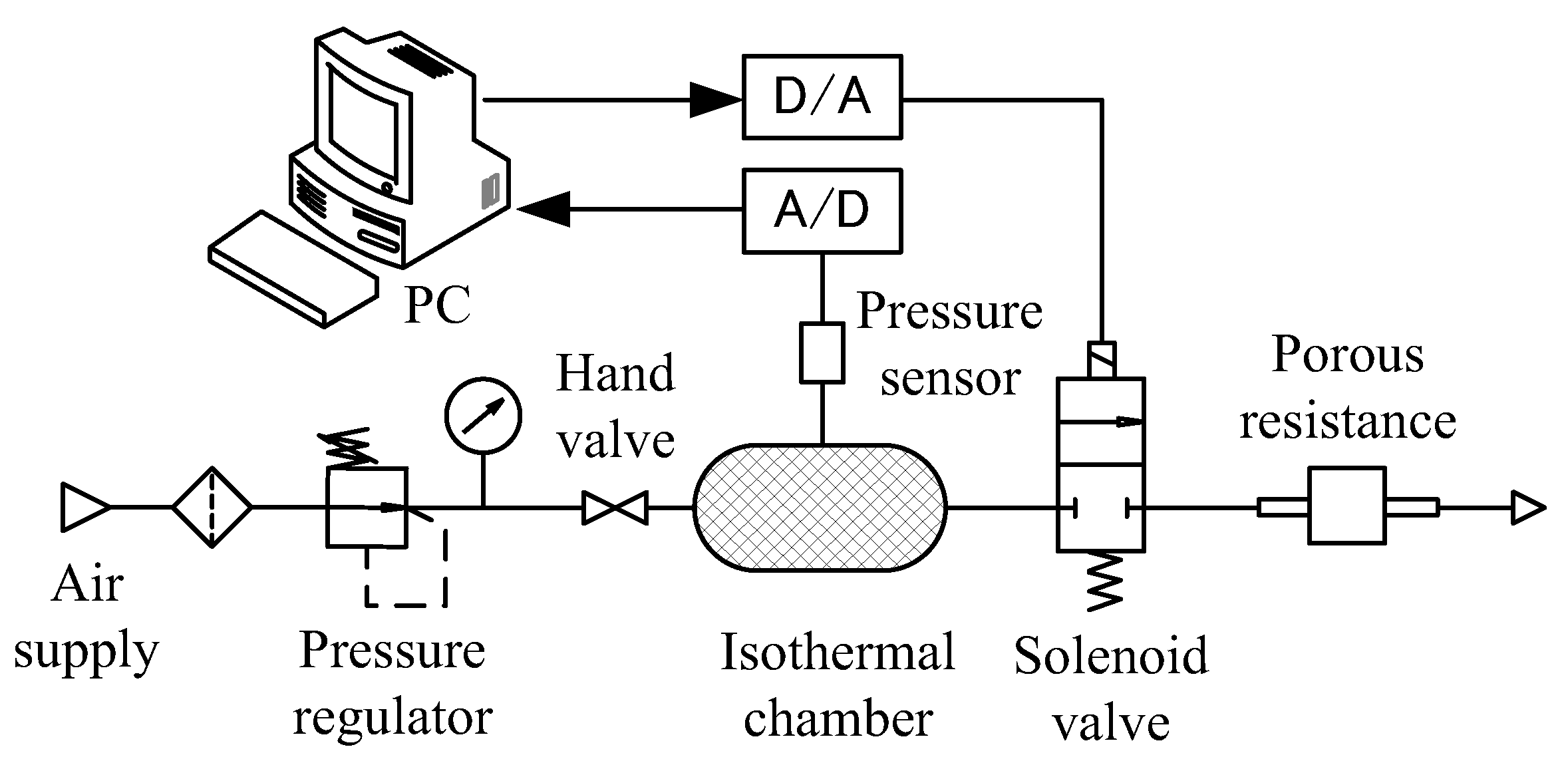
Figure 5 shows the experimental setup for the discharge method. An isothermal chamber that can provide almost isothermal condition is achieved by filling it with copper wire, which has a diameter of approximately 50 μm. The volume of the filled wire is about 5% compared with that of the chamber. The used isothermal chamber has a volume of 0.5 L, 0.65 L, and 0.8 L for the test samples of groups 1, 2 and 3, respectively. The procedure is simple in comparison with the steady-state method because it is not required to record data point by point. First, the solenoid valve is closed and the hand valve is opened to charge the chamber until its pressure reaches the regulated level. Then, close the hand valve and send a control signal to the solenoid valve to start the discharge process until the pressure in the chamber reaches the atmospheric pressure. A calibrated pressure sensor (GE Druck, UK, PTX5012, range: 0–1 MPa, accuracy: 0.1%) is used to measure the chamber pressure. The pressure data were transferred into a personal computer through a 14-bit A/D board (Advantech 4704), and the sampling time was 5 ms. The flow rate discharged from the isothermal chamber can be calculated according to the differentiated pressure, as below:
where Pc is the pressure in the chamber, t is the time, Vc is the volume of the chamber, R is gas constant, and θ is the room temperature.
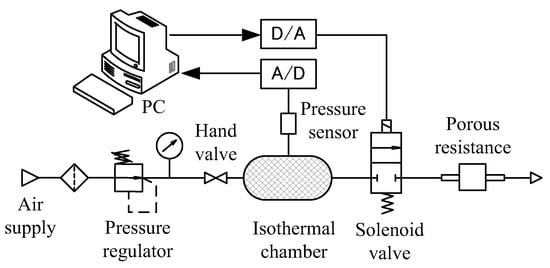
Figure 5.
Schematic of the apparatus for discharge method.
It should be noted that, in theory, both the charge method and the discharge method are capable of obtaining the flow rate characteristics of the test element. The discharge method is to discharge air through the test resistance into the atmosphere from a pressurized chamber, while the charge method uses a constant air supply to charge air into the chamber. However, in this work, the discharge method is preferred since the charge method exhibits a sudden drop in the upstream pressure at the start of the charging process.
4. Discussion
4.1. Results of the Steady-State Method
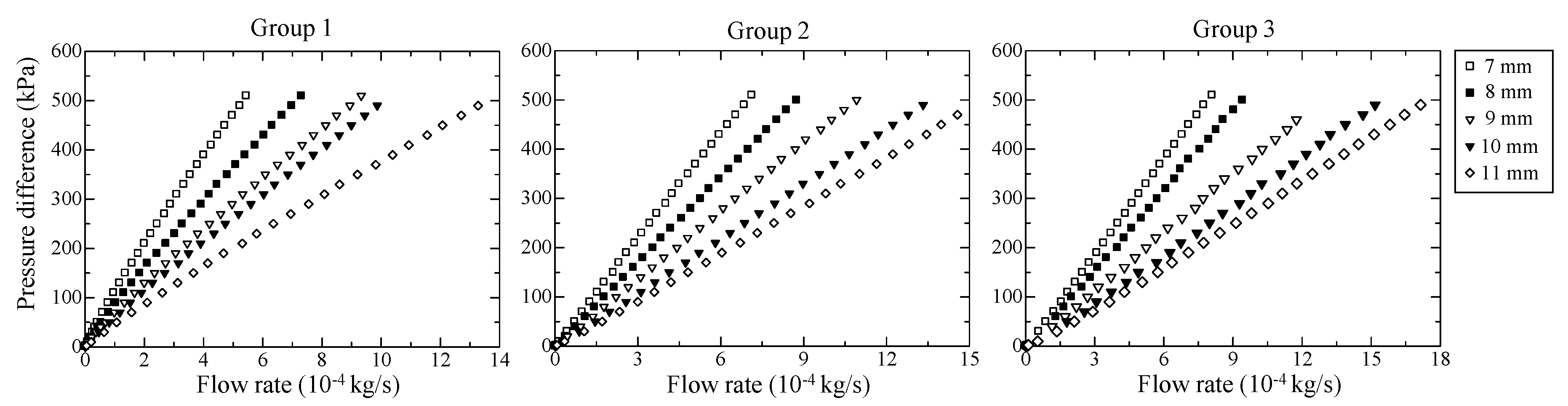
Figure 6 plots the pressure difference as a function of the mass flow rate for all the test media. The pressure difference increases with the flow rate and appears slightly nonlinear as the flow rate becomes adequately large. The viscous effect and the inertial effect can be viewed by permeability K and inertial coefficient β, which can be determined according to the modified Forchheimer equation. Observing these coefficients provides more insight than observing the pressure drop.
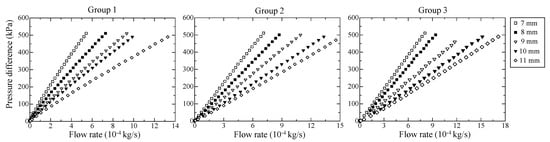
Figure 6.
Variation of measured pressure difference with mass flow rate.
The viscous effect dominates the flow pattern at a sufficiently small flow velocity, and in this case the Darcy equation can be used to characterize the flow behavior. However, how small flow velocity can be used as the boundary for the transition from viscous flow to inertial flow is unknown. To the best knowledge of the authors, it is almost impossible to define a universal boundary for the transition of regimes applicable to all kinds of porous media. Although some researchers presented a definite boundary of the Reynolds number for the regime transition, it depends on the properties of the porous material and the working fluid they used. For example, Dybbs and Edwards [36] reported that the boundary for viscous flow regime and inertial flow regime is Re = 1; however, it cannot be used in this work. For this problem, firstly, experiments are conducted under a slight pressure drop less than 3 kPa, where the air compressibility can be neglected and the pressure difference should exhibit a linear relationship with the flow rate. Figure 7 shows the measuring results in the form of pressure difference versus the mass flow rate. The data points are fitted using a least squares straight line, and the permeability can be calculated by the slope. The selected flow region proved appropriate since the R2 value of the fitting line exceeds 0.98.
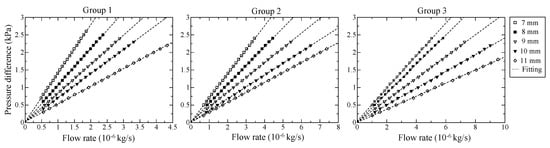
Figure 7.
Variation of measured pressure difference with mass flow rate under small pressure drops (<3 kPa).
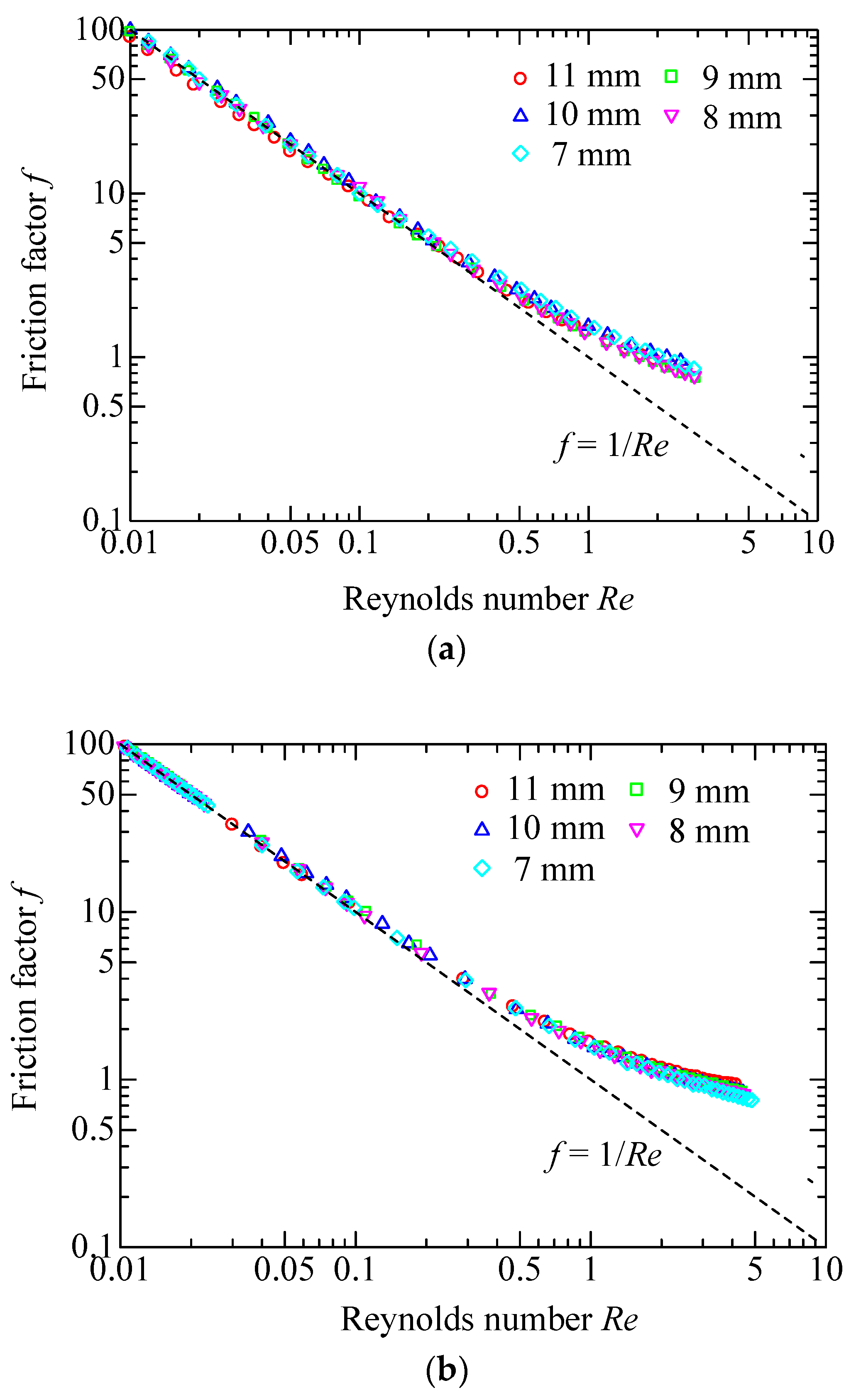
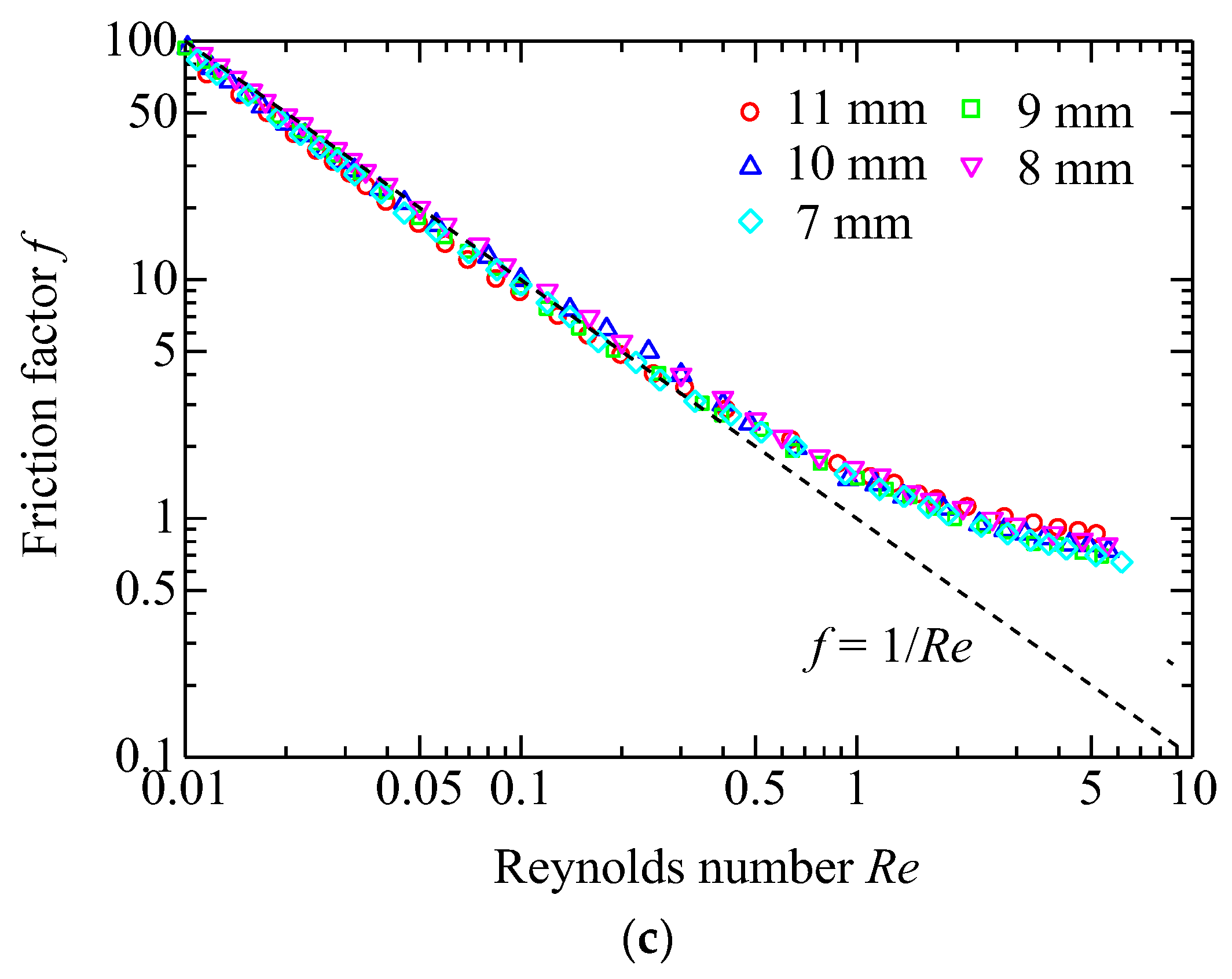
Then, experiments are conducted with large pressure drops. With the resulting permeability K, the inertial coefficient β is determined by the data points close to the maximum flow rate, where the inertial effect is regarded as completely dominating the flow pattern. Table 3 lists the determined coefficients K and β. In Figure 8, the experimental data for the samples of group 2 are presented in the form of friction factor versus Reynolds number, and the axes are plotted on a log-log scale. The Darcy equation in the form of f-Re is represented by a linear dashed line. Clearly, the data points significantly depart from the Darcy regime when Re > 0.1. Therefore, Re = 0.1 can be considered as the boundary separating the viscous flow from the inertial flow. Actually, there exists a transitional region between the viscous and inertial regimes; however, the region is uncertain and thus neglected in order to facilitate analysis. The maximum flow rate used for determination of the permeability for the media 7–11 mm (group 2) corresponds to the Reynolds number of 0.019, 0.024, 0.033, 0.039, and 0.052, respectively, and thus the reliability of the obtained permeability can be confirmed. Moreover, the friction factor converges to the inertial coefficient as the Reynolds number is adequately large. Taking group 2 as an example, the data points for the sample of 11 mm, 10 mm, 9 mm, 8 mm, and 7 mm can be well represented by analytical expressions f = 1/Re + 0.623, f = 1/Re + 0.578, f = 1/Re + 0.613, f = 1/Re + 0.585, and f = 1/Re + 0.522, respectively.

Table 3.
Permeability and inertia coefficients of the porous media by the steady-state method.
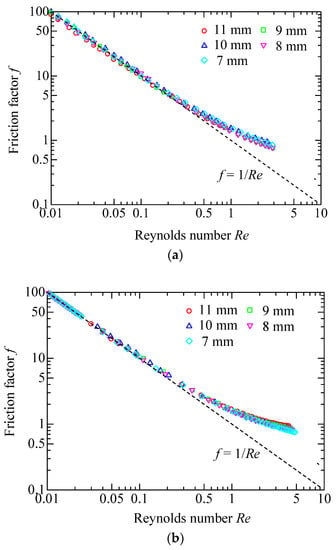
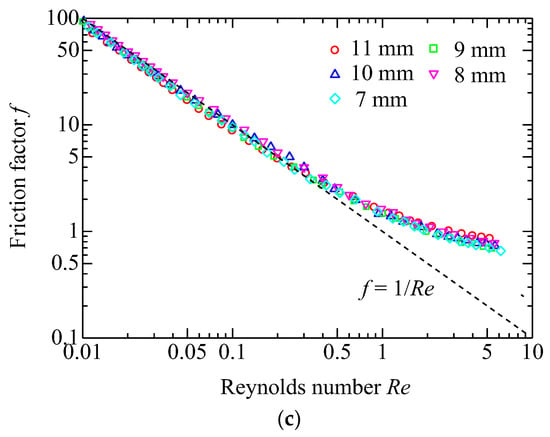
Figure 8.
Friction factor f as a function of the Reynolds number Re for the porous media. (a) Group 1; (b) Group 2; (c) Group 3.
4.2. Results of the Discharge Method
In the steady-state case, the permeability is first determined in the Darcy regime, and then the inertial coefficient is determined in the Forchheimer regime with the resulting permeability. This treatment is laborious since at least two types of flow sensors and pressure sensors with different ranges and accuracies are needed to satisfy the requirements of measurements across different flow ranges. During the discharge process, the instantaneous flow rate can be indirectly obtained thanks to the isothermal chamber, and the permeability and inertial coefficient can be simultaneously determined by Equation (4). If this method works, it will undoubtedly shortens the measuring time and greatly reduce the air consumption.
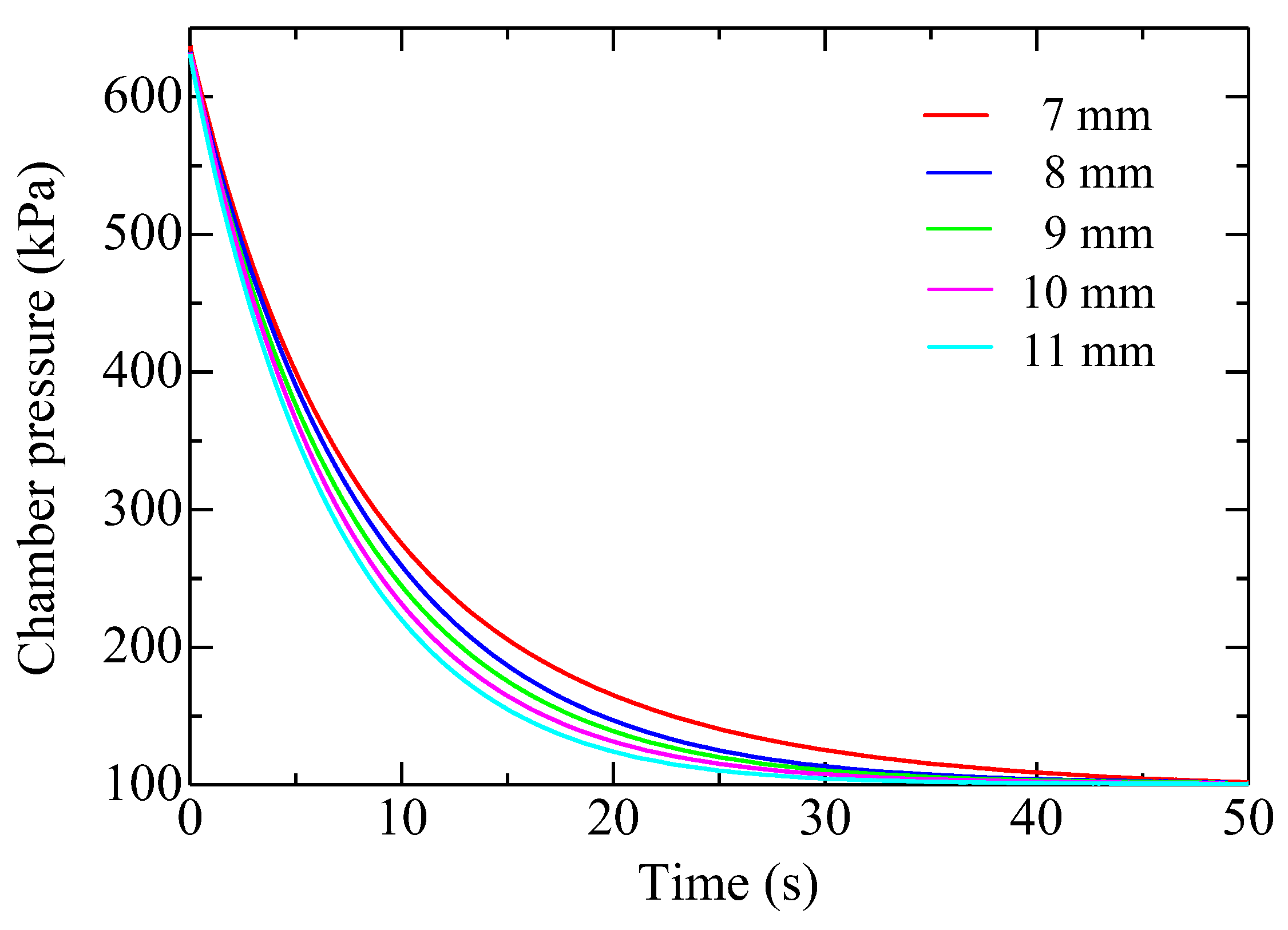
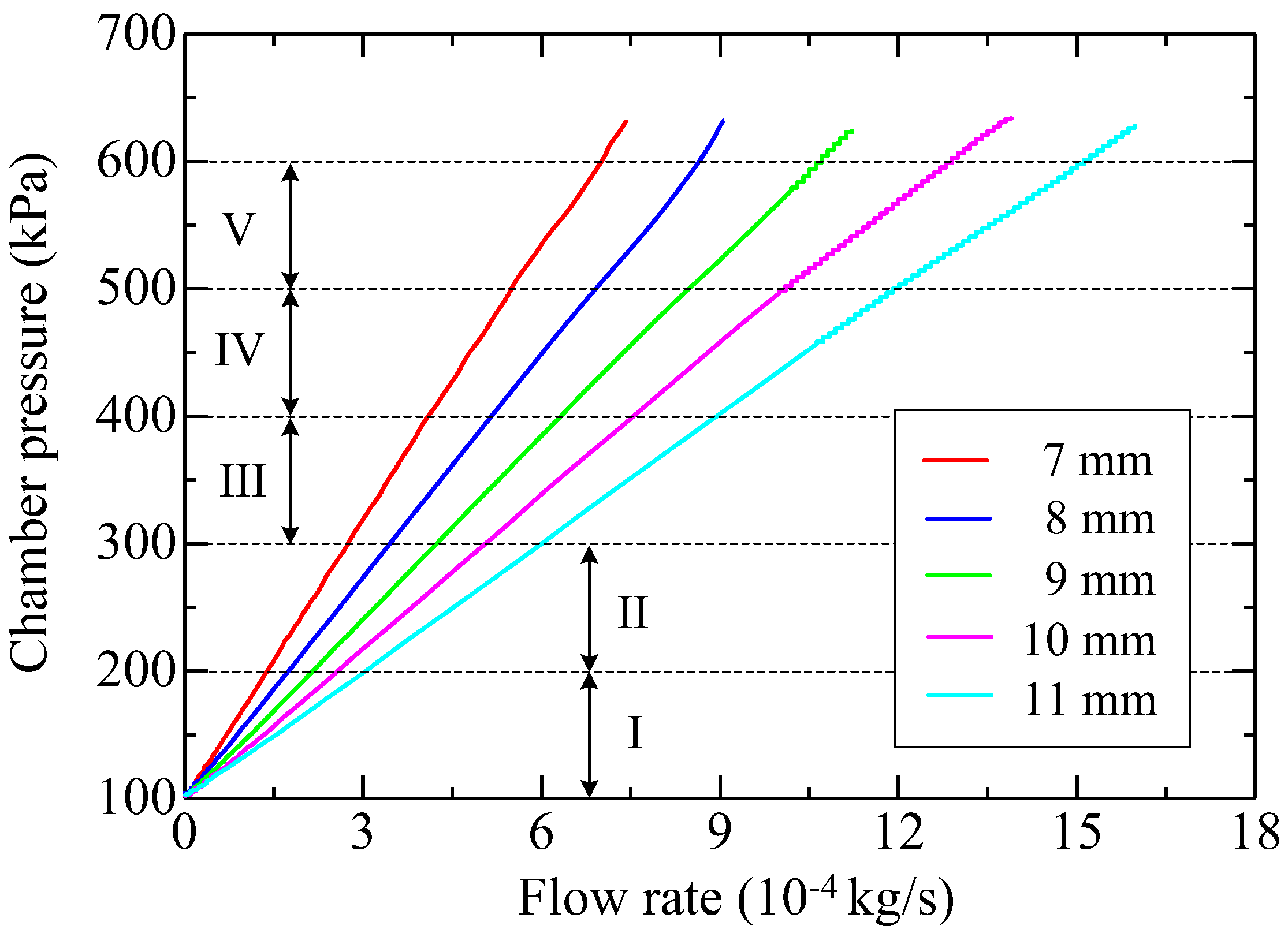
Figure 9 shows the pressure variation in the chamber during the discharge process for the samples of group 2. The initial data immediately after the opening of the valve are left because those data might include pressure disturbance. The acquired pressure data were first smoothed by the moving average method using 10 points, and then differentiated numerically with eight points to calculate the flow rate. Figure 10 shows the relation of chamber pressure versus the calculated mass flow rate. A subscript i, as the sequence number, is used to refer to any data point (e.g., chamber pressure Pi, mass flow rate Gi) in the dataset, and the number of the total data points is denoted as n. To facilitate iterative computation, Equation (4) is written in the following form:
where Pa is the atmospheric pressure.
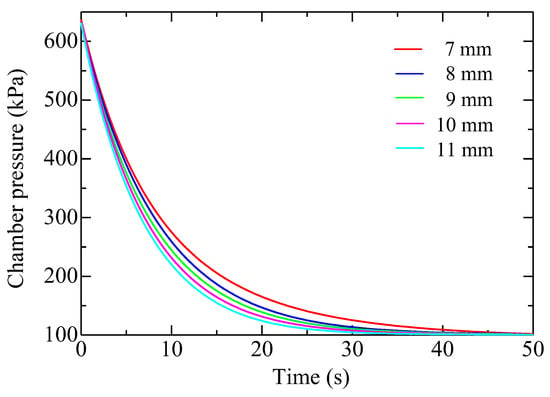
Figure 9.
Pressure in the chamber versus time during discharge process for the five porous media of group 2.
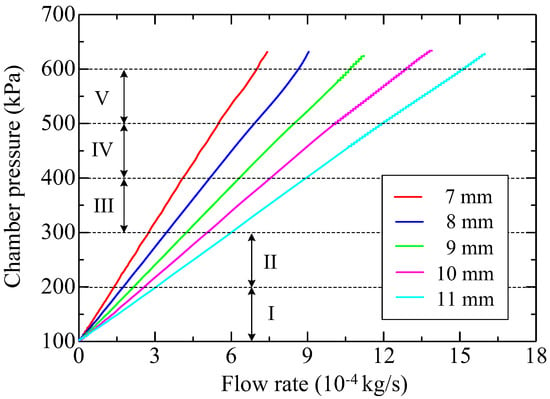
Figure 10.
Pressure in the chamber versus mass flow rate obtained by the discharge method for the five porous media of group 2.
Then, the permeability and inertial coefficient can be determined by the Gauss‒Newton fitting method using the following procedure:
- (1)
- Initial value K0 = 1 × 10−12 and β0 = 1 are given for the Forchheimer flow rate equation, Equation (10): .
- (2)
- The square residual error Spre is calculated by: . Here, The Gi values are obtained by differentiating the measured pressure in the chamber.
- (3)
- The elements of the first derivative , , and the residuals are calculated for i =1~n.
- (4)
- Solve the following two linear equations to obtain ΔK and Δβ.
- (5)
- Update K and β by K = K0 + ΔK and β = β0 + Δβ.
- (6)
- Calculate S = , if this value satisfies the convergence condition, i.e., |S − Spre| < ε, the determination process is ended. If it does not satisfy the condition, the aforementioned process is repeated with K0 and β0 replaced by K and β.
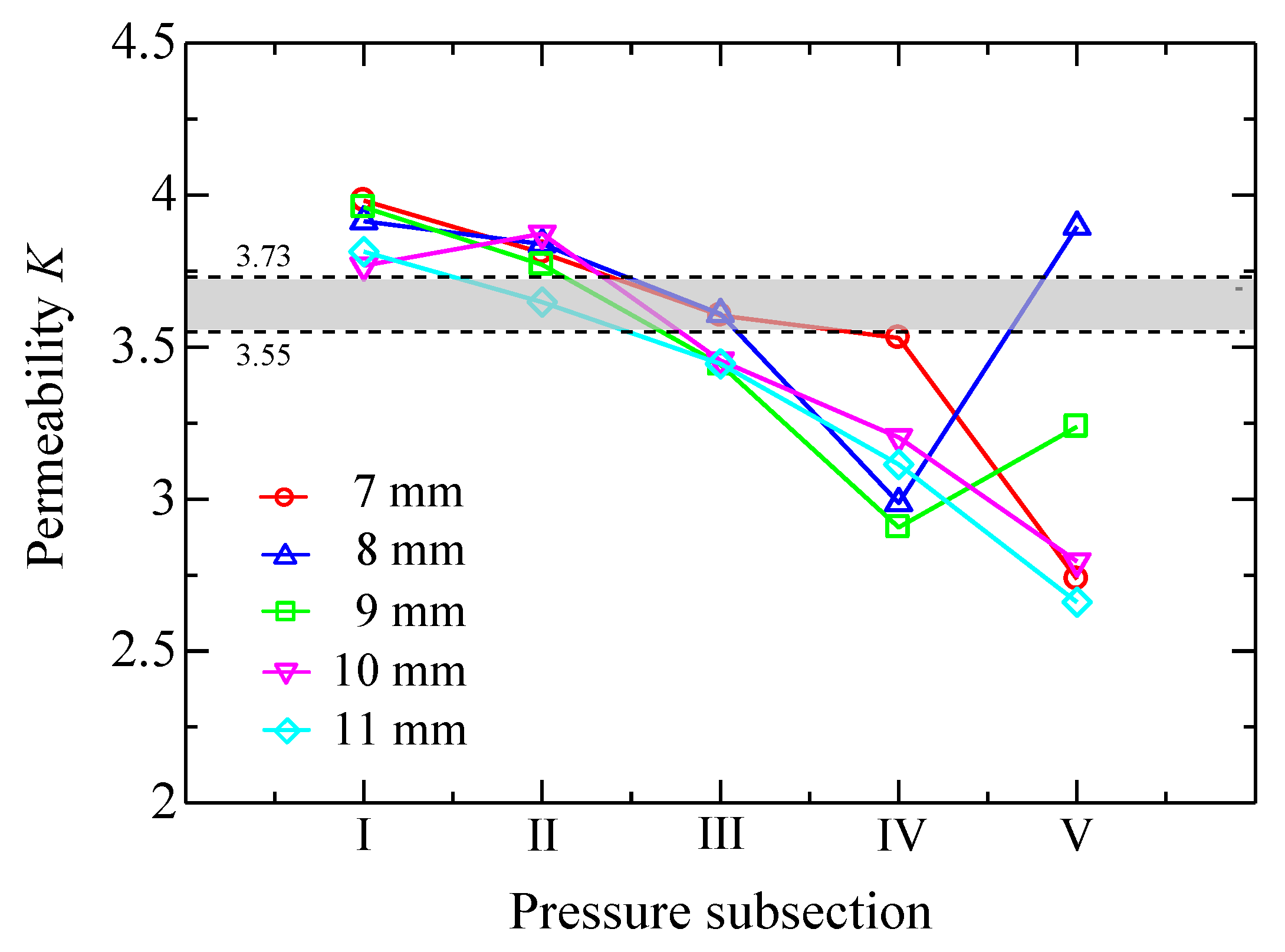
In Figure 10, five pressure subsections over the whole range, denoted as I, II, III, IV, and V, are uniformly divided from 100 kPa to 600 kPa to calculate the permeability. The measuring accuracy changes at different stages of the discharge process since the rate of pressure drop is always changing. The pressure bands are uniformly determined in order to find a satisfactory section to measure the permeability accurately. Figure 11 shows the permeability K determined by the discharge method in different pressure subsections for group 2. Objectively, the permeability should not change too much for different samples of the same group; however, for high-pressure subsections (IV and V), it exhibits significant alterations. That is probably because the collected data do not truly reflect the flow rate due to the rapid change of pressure in the chamber. For the steady-state case, the measured permeability ranges from 3.55 to 3.73. A gray belt that indicates the varying range is plotted in Figure 11 for an easy comparison. Clearly, the permeability determined using a medium-pressure dataset (II and III) accords with that of the steady-state results. In theory, the permeability should be determined in small flow regions. However, when the pressure in the chamber changes too slowly, it is probable that the measurement noise might be magnified and the low signal-to-noise ratio would result in significant uncertainties. Considering these, the datasets with the pressure ranging from 250 kPa to 350 kPa are extracted and used to determine the permeability K and inertial coefficient β, which are listed in Table 4. Actually, the dataset with the pressure ranging from 250 kPa to 350 kPa is only a small subset of the whole range. Taking the 11 mm sample (group 2) as an example, 250 kPa–350 kPa corresponds to the Reynolds number of 1.13–1.87. It is thus concluded that the data in the form of f versus Re taken with the discharge method cannot completely reflect the characteristics compared to the steady-state method.
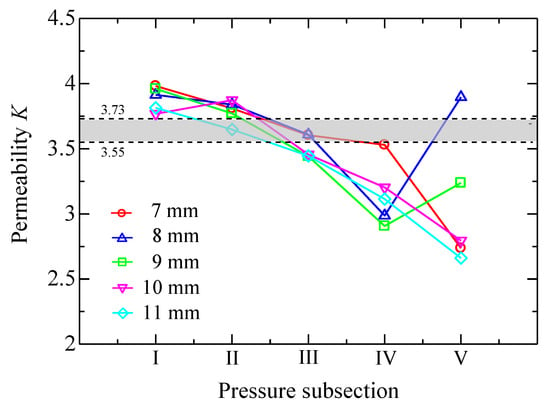
Figure 11.
Permeability obtained by the discharge method in different pressure subsections for the five porous media of group 2.

Table 4.
Results of fitting coefficients K and β by the discharge method.
4.3. Comparison of the Steady-State Method and the Discharge Method
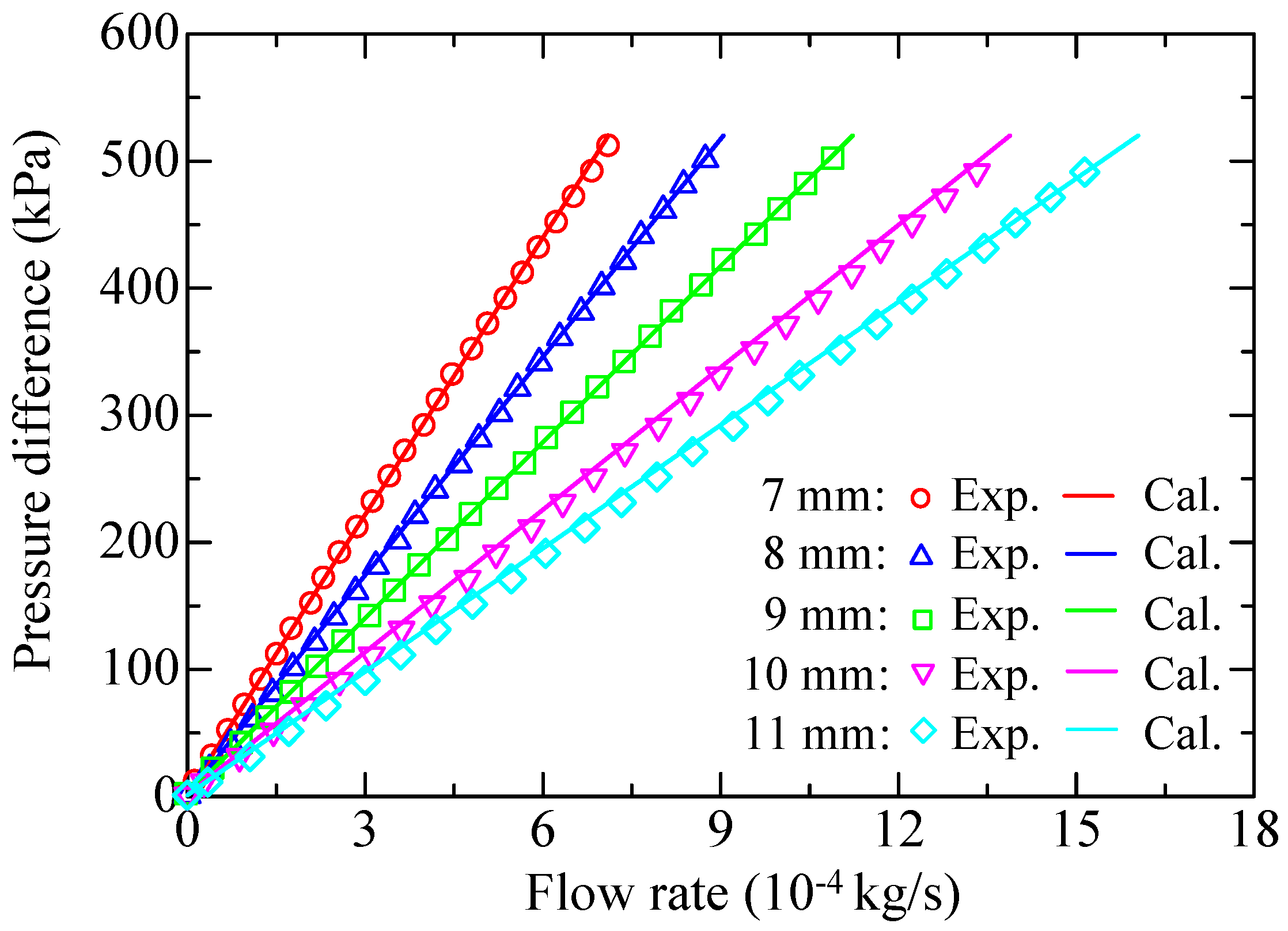
Figure 12 compares the steady-state results and the calculated results with the determined coefficients by the discharge method. The calculated curves agree with the steady-state data points on the whole, indicating that the discharge method works well for obtaining the property coefficients. To evaluate the discharge method, the accuracies of the method are calculated and compared with that of the steady-state method, which was proven viable in a previous work [28]. The error E is expressed as
where G(exp)i is for the steady-state flow rate, and G(cal)i is for the calculated flow rate.
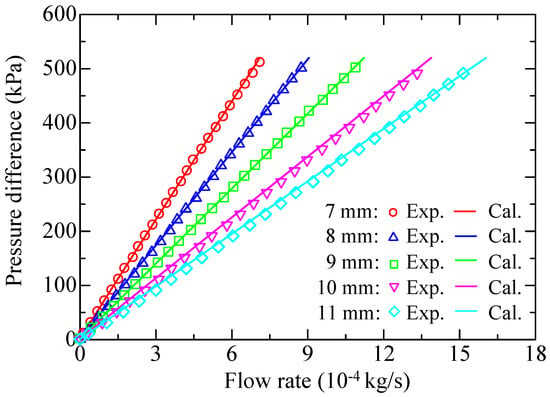
Figure 12.
Comparison of the theoretical and experimental flow rate characteristics for the five porous media of group 2.
The results in Table 5 show that the calculated results can achieve an accuracy within 3%. However, referring to one of the previous works of the authors, the calculated results with the property coefficients determined by the steady-state method can achieve an accuracy within 1% in the Forchheimer flow region. This is probably because the flow rate in the current work is obtained by differentiating the measured pressure with respect to time, and this treatment would magnify the noise and deteriorate the measuring accuracy. Taking one of the previous works by Kawashima et al. as another example, the sonic conductance C determined by the discharge method following the ISO 6358 equation can achieve an accuracy within 2% while the permeability in the current work is 5–10%. Despite a larger deviation in the coefficients, the accuracy of the theoretical flow rate over the entire range is sufficient for most applications.

Table 5.
Deviations from the experimental data by the steady-state method and the discharge method.
The key point of the discharge method is that the isothermal chamber must remain isothermal during the measuring process. If the selected chamber has a very small volume, the isothermal condition cannot be maintained due to the rapidly changing pressure. Previous research [32] implies that the temperature variation can be limited within 3K when the pressure change is less than 100 kPa/s. That is, for group 2, the lower limit volumes for 7–11 mm samples are 0.28 L, 0.34 L, 0.43 L, 0.48 L and 0.62 L, respectively. Inversely, if the chamber volume is too large, the measured pressure change is almost equal to the sensor resolution, and this also deteriorates the measuring accuracy. In the experiments, it is considered that at least 20 kPa/s is needed. Therefore, the upper limit volumes for 7–11 mm samples (group 2) are 0.85 L, 1.04 L, 1.27 L, 1.46 L, and 1.88 L, respectively. In Figure 12, careful observation shows that the 11-mm sample exhibits more apparent deviation from the steady-state data points than others. This is because the selected volume of the isothermal chamber is very close to the lower limit, and probably the isothermal condition cannot be strictly maintained during the discharge process.
The discharge method greatly reduces the test time and air consumption. In the steady-state case, flow measurement is maintained for a while to reduce the measuring error. Taking the sample of 11 mm (group 2) as an example, the maximum flow is maintained for at least 30 s to ascertain the inertial coefficient, and thus the air consumption is about 39 L (ANR). Noted that ANR (Atmosphere Normale de Reference) after the unit depicts air volume at conditions 101.325 kPa absolute, 20 °C, and 65% relative humidity. For the discharge method, the testing procedure is comparatively simple because it can be finished in a few seconds, and the consumed air is the amount of compressible air initially stored in the chamber, which is about 4 L (ANR).
5. Conclusions
This study proposes a discharge method to determine the flow characteristics of sintered metal porous media using an isothermal chamber. The pressure in the chamber is measured and then differentiated to calculate the discharged flow rate. Fifteen samples, categorized into three groups, are employed as the test element to perform the experiments. A modified Forchheimer equation is constructed to represent the relationship between flow rate and pressure difference in terms of the permeability and inertial coefficients. First, the coefficients are determined per the steady-state method by determining first the permeability in the Darcy region and then the inertial coefficient in the Forchheimer region. The Darcy and Forchheimer regions were defined with a Reynolds number of 0.1 as the boundary. Then, with the discharge method, the coefficients are simultaneously determined in five uniformly distributed pressure subsections. The results of permeability in comparison with the steady-state results indicate that using a medium-pressure dataset (250 kPa–350 kPa) improves the accuracy. Although the permeability and inertial coefficients determined by the discharge method somewhat deviate from those of the steady-state method, the theoretical calculation can represent the flow rate characteristics within 3% accuracy compared with the experimental results indicating that the traditional method can be replaced by the discharge method, which greatly shortens the measuring time, with only 10% air consumption as in the steady-state method. However, an appropriate volume for the isothermal chamber is necessary to ensure the measuring accuracy because the discharge method requires a reasonable discharging speed.
The presented results indicate that the discharge method has potential for use in industry. As an example, in air-bearing systems, a large number of porous pads are employed and their flow properties are required to be as consistent as possible. A lot of testing and analysis are needed to help evaluate the manufacturing process. In this case, the discharge method is very useful since it facilitates the procedures and greatly reduces the air consumption under the premise of ensuring the accuracy.
The limitations of the present study lie in the following aspects:
- (1)
- The test samples are mainly tight porous media, which have a permeability on the order of 10−12 m2 and are generally applied in air-bearing systems.
- (2)
- An isothermal condition for the chamber is necessary during the discharge process. Otherwise, the calculated flow rate would exhibit large error. This means that a reasonable discharge speed is required.
- (3)
- The theoretical model is somewhat realistic since the inner structure of the actual porous media is not uniform. Therefore, the determined coefficients might not reflect the true properties of the media.
- (4)
- Only the permeability and inertial coefficients are discussed. The influences of other parameters such as porosity φ, cross-sectional area A, and length of the medium L are not included.
Author Contributions
Conceptualization, W.Z.; Data curation, X.J.; Investigation, J.F.; Methodology, X.J. and C.L.; Resources, C.L.; Validation, J.F.; Writing—original draft, W.Z.; Writing—review & editing, F.L.
Funding
This study was supported by the National Natural Science Foundation of China (Grant No. 51675247).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | cross-sectional area (m2) |
| G | mass flow rate (kg/s) |
| G(cal)i | calculated flow rate (kg/s) |
| G(exp)i | steady-state flow rate (kg/s) |
| K | permeability (m2) |
| L | length of the test medium (m) |
| m | mass of the medium (kg) |
| P | pressure (Pa) |
| P1 | upstream pressure (Pa) |
| P2 | downstream pressure (Pa) |
| Pa | atmospheric pressure (Pa) |
| Pc | pressure in the chamber (Pa) |
| R | gas constant |
| t | time (s) |
| T | temperature (K) |
| V | total volume (m3) |
| Vc | volume of the chamber (m3) |
| β | inertial coefficient |
| γ | metal density (8.03 × 103 kg/m3) |
| Θ | room temperature (K) |
| μ | air viscosity (Pa⋅s) |
| v | velocity (m/s) |
| ρ | density (kg/m3) |
| φ | porosity |
Appendix A
ISO 6358 is an international standard that specifies a method for testing pneumatic components to represent their flow rate characteristics under steady-state conditions. The ISO 6358 equation, which is deduced from isentropic flow through a perfect nozzle, is provided in the ISO 6358 standard. The ISO 6358 equation depicts flow rate characteristics with two independent parameters: sonic conductance C and critical pressure ratio b. Two flow states, choked flow and subsonic flow, are defined according to the relationship between the pressure ratio P2/P1 and the critical pressure ratio b. When P2/P1 ≤ b, choked flow occurs; when P2/P1>b, subsonic flow occurs. The ISO 6358 equation is written in the following form:
where C is the sonic conductance, b is the critical pressure ratio, ρ0 is the air density under normal condition, P1 is the upstream pressure, P2 is the downstream pressure, and T is the temperature.
References
- Liao, Y.; Li, X.; Zhong, W. Experimental study of pressure drop-flow rate characteristics of heated tight porous materials. J. Fluids Eng. 2016, 138, 071102. [Google Scholar] [CrossRef]
- Liao, Y.; Li, X.; Zhong, W. Study of pressure drop-flow rate and flow resistance characteristics of heated porous materials under local thermal non-equilibrium conditions. Int. J. Heat Mass Tran. 2016, 102, 528–543. [Google Scholar] [CrossRef]
- Lage, J.L.; Antohe, B.V.; Nield, D.A. Two Types of Nonlinear Pressure-Drop versus Flow-Rate Relation Observed for Saturated Porous Media. J. Fluids Eng. 1997, 119, 700–706. [Google Scholar] [CrossRef]
- Andrade, J.S.; Costa, U.M.S.; Almeida, M.P.; Makse, H.A.; Stanley, H.E. Inertial effects on fluid flow through disordered porous media. Phys. Rev. Lett. 1999, 82, 5249–5252. [Google Scholar] [CrossRef]
- Boomsma, K.; Poulikakos, D. The effects of compression and pore size variations on the liquid flow characteristics in metal foams. J. Fluids Eng. 2002, 124, 263–272. [Google Scholar] [CrossRef]
- Medraj, M.; Baril, E.; Loya, V.; Lefebvre, L.P. The effect of microstructure on the permeability of metallic foams. J. Mater. Sci. 2007, 42, 4372–4383. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 3rd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Nihad, D.; Özer, B.; Mustafa, Ö. Experimental flow in various porous media and reconciliation of Forchheimer and Ergun relatons. Exp. Therm. Fluid Sci. 2014, 57, 425–433. [Google Scholar]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Macdonald, I.F.; EI-Sayed, M.S.; Mow, K.; Dullien, F.A.L. Flow through porous media-the Ergun Equation Revisited. Ind. Eng. Chem. Fundam. 1979, 18, 199–208. [Google Scholar] [CrossRef]
- Beavers, G.S.; Sparrow, E.M. Non-Darcy flow through fibrous porous media. J. Appl. Mech. 1969, 36, 711–714. [Google Scholar] [CrossRef]
- Beavers, G.S.; Sparrow, E.M.; Rodenz, D.E.J. Influence of bed size on the flow characteristics and porosity of randomly packed beds of spheres. Appl. Mech. 1973, 40, 655–660. [Google Scholar] [CrossRef]
- Montillet, A.; Akkari, E.; Comiti, J. About a correlating equation for predicting pressure drops through packed beds of spheres in a large range of Reynolds numbers. Chem. Eng. Process 2007, 46, 329–333. [Google Scholar] [CrossRef]
- Antohe, B.V.; Lage, J.L.; Price, D.C.; Weber, R.M. Experimental determination of permeability and inertia coefficients of mechanically compressed aluminum porous matrices. J. Fluids Eng. 1997, 119, 404–412. [Google Scholar] [CrossRef]
- Dukhan, N.; Minjeur, C.A., II. A two-permeability approach for assessing flow properties in metal foam. J. Porous Mat. 2011, 18, 417–424. [Google Scholar] [CrossRef]
- Liu, J.F.; Wu, W.T.; Chiu, W.C.; Hsieh, W.H. Measurement and correlation of friction characteristic of flow through foam matrixes. Exp. Therm. Fluid Sci. 2006, 30, 329–336. [Google Scholar] [CrossRef]
- Dukhan, N.; Patel, P. Equivalent particle diameter and length scale for pressure drop in porous metals. Exp. Therm. Fluid Sci. 2008, 32, 1059–1067. [Google Scholar] [CrossRef]
- Dietrich, B.; Schabel, W.; Kind, M.; Martin, H. Pressure drop measurements of ceramic sponges—Determining the hydraulic diameter. Chem. Eng. Sci. 2009, 64, 3633–3640. [Google Scholar] [CrossRef]
- Kim, T.; Lu, T.J. Pressure drop through anisotropic porous mediumlike cylinder bundles in turbulent flow regime. J. Fluids Eng. 2008, 130, 104501. [Google Scholar] [CrossRef]
- Jin, L.W.; Kai, C.L. Pressure drop and friction factor of steady and oscillating flows in open-cell porous media. Transp. Porous Med. 2008, 72, 37–52. [Google Scholar] [CrossRef]
- Mancin, S.; Zilio, C.; Cavallini, A.; Rossetto, L. Pressure drop during air flow in aluminum foams. Int. J. Heat Mass Tran. 2010, 53, 3121–3130. [Google Scholar] [CrossRef]
- Belforte, G.; Raparelli, T.; Viktorov, V.; Trivella, A. Metal woven wire cloth feeding system for gas bearings. Tribol. Int. 2009, 42, 600–608. [Google Scholar] [CrossRef]
- Belforte, G.; Raparelli, T.; Viktorov, V.; Trivella, A. Permeability and inertial coefficients of porous media for air bearing feeding systems. J. Tribol-T. Asme 2007, 129, 705–711. [Google Scholar] [CrossRef]
- Rodrigo, N.; Zilda, C.S.; Benedito, M.P. Modified Reynolds Equation for Aerostatic Porous Radial Bearings with Quadratic Forchheimer Pressure-Flow Assumption. J. Tribol-T. Asme 2008, 130, 031701. [Google Scholar]
- Amano, K.; Yoshimoto, S.; Miyatake, M.; Hirayama, T. Basic investigation of noncontact transportation system for large TFT-LCD glass sheet used in CCD inspection section. Precis. Eng. 2011, 35, 58–64. [Google Scholar] [CrossRef]
- Oiwa, N.; Masuda, M.; Hirayama, T.; Matsuoka, T.; Yabe, H. Deformation and flying height orbit of glass sheets on aerostatic porous bearing guides. Tribol. Int. 2012, 48, 2–7. [Google Scholar] [CrossRef]
- Miyatake, M.; Akahori, H.; Yoshimoto, S. Deformation of large liquid crystal display glass sheets across a gap between noncontact transportation devices. Precis. Eng. 2016, 46, 360–368. [Google Scholar] [CrossRef]
- Zhong, W.; Li, X.; Liu, F.H.; Tao, G.; Lu, B.; Kagawa, T. Measurement and Correlation of Pressure Drop Characteristics for Air Flow through Sintered Metal Porous Media. Transp. Porous. Med. 2014, 101, 53–67. [Google Scholar] [CrossRef]
- Zhong, W.; Xu, K.; Li, X.; Kagawa, T. Study on the basic characteristics of a noncontact air conveyor for large glass sheets. Adv. Mech. Eng. 2017, 9, 1–13. [Google Scholar] [CrossRef]
- Zhong, W.; Li, X.; Tao, G.L.; Kagawa, T. Measurement and Determination of Friction Characteristic of Air Flow through Porous Media. Metals 2015, 5, 336–349. [Google Scholar] [CrossRef]
- Zhong, W.; Xu, K.; Li, X.; Liao, T.; Tao, G.; Kagawa, K. Determination of pressure drop for air flow through sintered metal porous media using a modified Ergun equation. Adv. Powder Technol. 2016, 27, 1134–1140. [Google Scholar] [CrossRef]
- Kawashima, K.; Ishii, Y.; Funaki, T.; Kagawa, T. Determination of flow rate characteristics of pneumatic solenoid valves using an isothermal chamber. J. Fluid. Eng-T. Asme 2004, 126, 273–279. [Google Scholar] [CrossRef]
- Dukhan, N.; Ali, M. Strong wall and transverse size effects on pressure drop of flow through open-cell metal foam. Int. J. Therm. Sci. 2012, 57, 85–91. [Google Scholar] [CrossRef]
- Eisfeld, B.; Schnitzlein, K. The influence of confining walls on the pressure drop in packed beds. Chem. Eng. Sci. 2001, 56, 4321–4329. [Google Scholar] [CrossRef]
- Akbarnejad, S.; Pour, M.S.; Jonsson, L.T.I.; Jönsson, P. Effect of fluid bypassing on the experimentally obtained Darcy and non-Darcy permeability parameters of ceramic foam filters. Metall. Mater. Trans. 2016, 48, 197–207. [Google Scholar] [CrossRef]
- Dybbs, A.; Edwards, R.V. A new look at porous media fluid mechanics—Darcy to Turbulent. In Fundamentals of Transport Phenomena in Porous Media; Bear, J., Corapcioglu, M.Y., Eds.; Springer Netherlands: Berlin, Germany, 1984; Volume 82, pp. 199–256. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).