Reliability Modeling and Evaluation Method of CNC Grinding Machine Tool

Featured Application

The proposed research aims to provide one accurate and reliable evaluation method for the subsystem and system of electromechanical equipment.

Abstract

How to determine subsystem’s reliability and evaluate the whole machine’s reliability of the CNC (computer numerical control) grinding machine tool is important for reliability design and promotion. Each subsystem was modeled by a different distribution based on collected data and the models were optimized by the modified gray correlation degree, which was called the similar slope and close median gray correlation method. Methods of generating random data were proposed for different models. The reliability evaluation algorithm based on Monte Carlo simulation was studied and the whole machine’s reliability of the CNC grinder was evaluated by the algorithm. The evaluation result by the Monte Carlo algorithm was compared using the observed value and the evaluation value by the whole fitting method. The results show that the point estimation value evaluated by the algorithm based on Monte Carlo has high accuracy. The interval estimation by the Monte Carlo method was 20.2% and 38.1% by the observed value and the whole fitting value, respectively, which has more practical engineering significance. The reliability evaluation method can be used to assess the whole CNC grinding machine’s reliability in reliability design, and is also one reference for reliability evaluation of other electromechanical equipment.

1. Introduction

The CNC (computer numerical control) grinding machine tool is widely used in automotive, aircraft, and other industries to grind precise parts as the last process, and its reliability has an important influence on the processing quality and production efficiency. At present, high-performance CNC machine tools require reliability design. Reliability assessment is an important part of the reliability design. From reliability evaluation, the designer can not only understand the reliability level of the current equipment, they can also find the weak link, as well as test whether or not the reliability design meets the requirements. At the same time, reliability evaluation can select the outsourcing products whose reliability meets the requirements.

There are many reliability evaluation methods and scholars have conducted extensive research on the reliability evaluation of machine tools or similar equipment. The reliability of the CNC machine tool was evaluated using a go-flow methodology by Yu et al. [1]. The reliability of the CNC machine tool was analyzed and evaluated using three parameters of the Weibull distribution by Zhang et al. [2]. The reliability of the CNC machine tool was evaluated using the exponential distribution by Dai et al. [3]. The tool reliability of the CNC machine was evaluated using the logistic model by Chen et al. [4]. The reliability of the structural system was reassessed using the Bayesian network by Sankaran et al. [5]. The reliability was analyzed through reliability data and evaluated using the maximum likelihood estimation by David et al. [6]. The reliability of the machining center was evaluated using failure mode analysis by Kim et al. [7]. The reliability of the drilling machine was evaluated using neural network and wavelet analysis by Chinnam et al. [8]. The reliability of typical modular mechanical equipment was evaluated using the Weibull distribution by Neumann et al. [9]. Sung proposed the lifetime estimation method by accelerated degradation test [10]. Cheng et al. used Monte Carlo simulation to analyze the machine tool’s machining accuracy reliability [11]. Wei et al. proposed one reliability assessment method for mechanical equipment using the performance-feature model [12]. The cutting tool’s reliability was predicted based on acoustic emission and logistic regression model by Hongkun et al. [13]. There are some shortcomings of the current research. (1) The machine is usually regarded as one whole to study on the condition that the reliability data are not enough. (2) The distribution of the whole machine is usually supposed as the exponential distribution or Weibull distribution. In fact, the CNC machine tool is one complex mechanical, electrical, and hydraulic system. Furthermore, the distribution model of each component is not same and the difference is ignored by the above method (signed as the whole fitting method). The pertinence is not strong in reliability design by the whole fitting method. Different subsystems of the CNC grinding machine are designed and manufactured by different enterprises; at this point, subsystem division and studying have more practical significance than the whole fitting method.

In order to evaluate the reliability accurately of CNC grinding machine tools with less field data, one system reliability evaluation method for each subsystem of the CNC machine tool being modeled, as well as then running Monte Carlo simulation, was proposed in the paper, which makes the evaluation scope narrower and means that it has more engineering significance.

2. Modeling of Subsystem

2.1. Reliability Models

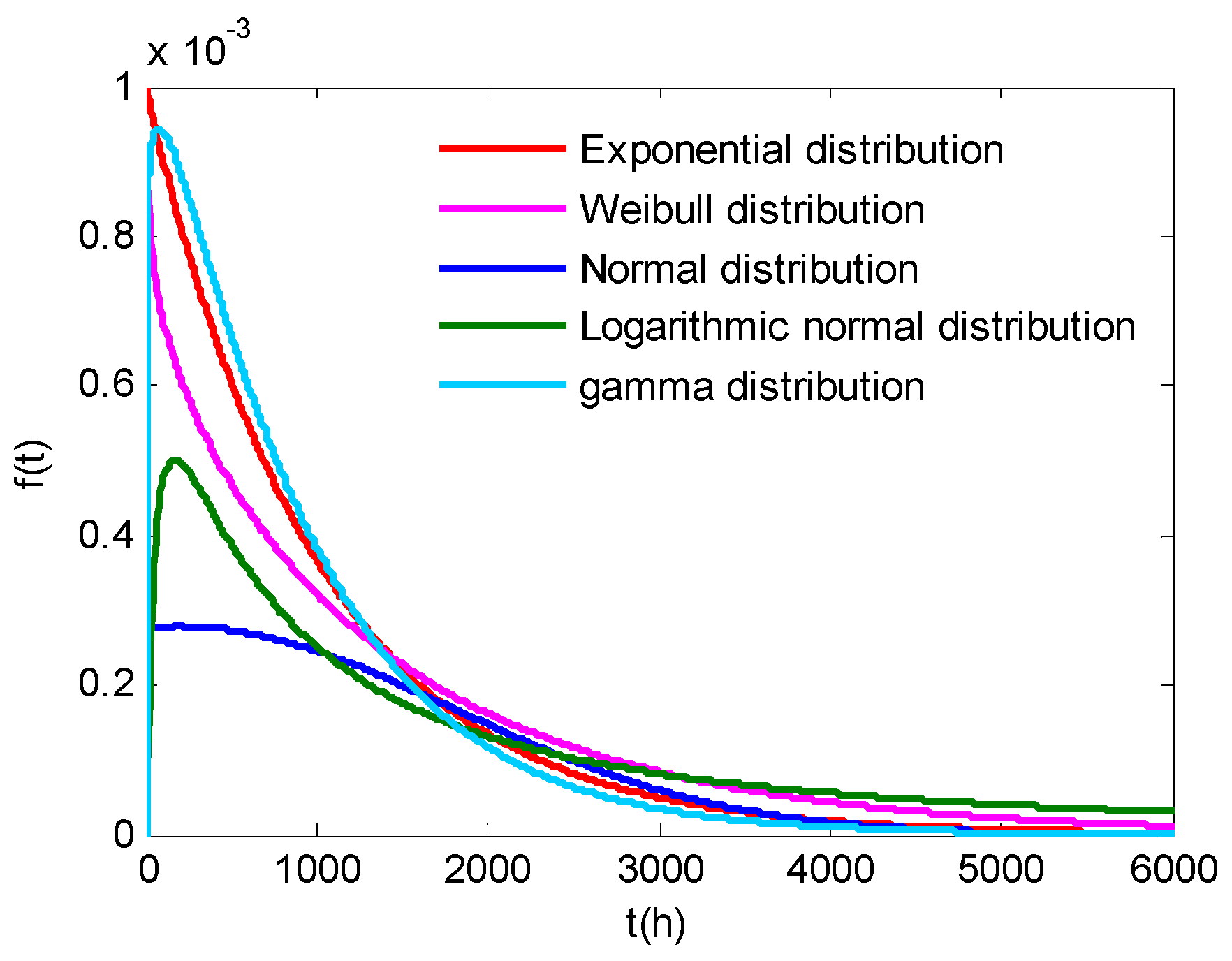
The CNC grinding machine can be divided into different subsystems according to their structure and function, and the distribution types of each subsystem are not same. The fault rate curves of mechanical and electrical products or components are similar to the “bathtub curve”, and usually only the first and second paragraphs of the bathtub curve are studied, which are the early failure period and occasional failure period. In statistics, there are many distribution types that are close to the bathtub curve, such as the exponential distribution, Weibull distribution, normal distribution, lognormal distribution, gamma distribution, and so on, as shown in Figure 1. The probability density functions of the above-mentioned five distribution types are shown in Equations (1) to (5). In this paper, five distribution models are used to fit for each subsystem separately, and the optimum model for each subsystem is selected.

$$f(t)=\lambda e^{-\lambda t}$$

(1)

$$f(t)=\frac{\beta }{\eta }{\left(\frac{t-\gamma }{\eta }\right)}^{\beta -1}\exp \left(-{\left(\frac{t-\gamma }{\eta }\right)}^{\beta }\right)$$

(2)

$$f(t)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{{(t-\mu )}^2}{2{\sigma }^2}\right)$$

(3)

$$f(t)=\frac{1}{{\sigma }_{l}t\sqrt{2\pi }}\exp \left(-\frac{{(\ln t-{\mu }_l)}^2}{2{\sigma }_l{}^2}\right)$$

(4)

$$f(t)=\frac{1}{b^a\Gamma (a)}{t}^{a-1}{e}^{-\frac{t}{b}}$$

(5)

2.2. Reliability Data Grouping

Reliability data are needed for reliability modeling. Reliability data should be classified to each subsystem. The maximal time between failures can be divided equally into k intervals and the reliability data can be classified into the corresponding intervals for each subsystem. The value of k can be from 6 to 10. The fault number and probability density can be calculated as shown in

Table 1. Reliability data acquiring and grouping.

Group Number	ti–	ti	ti+	ni	fi
1	0	tm/2k	tm/k	n1	f1
2	tm/k	3tm/2k	2tm/k	n2	f2
…	…	…	…	…	…
k	(k-1)∙tm/k	(2k-1)∙tm/2k	tm	nk	fk

Note: t_m: the maximal time between failures; t_i–: the left end of the ith time interval; t_i+: the right end of the ith time interval; t_i: the median of the ith time interval; n_i: the fault number of the ith time interval; f_i: the probability density of the ith time interval, which can be calculated by Equation (6). In Equation (6), Δt is the time interval length.

.

$$f_i=\frac{n_i}{\Delta t{\displaystyle \sum n_i}}$$

(6)

2.3. Probability Density Function Fitting

After the probability density of each interval is calculated, the k group data pair can be obtained as (t_i, f_i). The probability density function can be fitted according to the data pair using the least squares method or maximum likelihood method for each subsystem by different distribution type, and the point estimation and interval estimation of the parameters of the probability density function can be executed [14].

2.3.1. Exponential Distribution

The accumulative distribution function of the exponential distribution is shown in Equation (7) and has one parameter, λ.

$$F(t_i)=1-e^{-\lambda t_i}$$

(7)

Taking the logarithm on both sides of Equation (7), the linear equation can be created. If the sample data meet exponential distribution, t_i and $\ln [1-F(t_i)]$ are linear and the observed value of parameters λ can be calculated by Equation (8).

$$\widehat{\lambda }=-a$$

(8)

2.3.2. Weibull Distribution

The accumulative distribution function of the two-parameter Weibull distribution is shown in Equation (9) and has two parameters, m and η.

$$F(t_i)=1-\exp [{-(t_i/\eta )}^m]$$

(9)

Taking the logarithm twice on both sides of Equation (9) and supposing $y=\ln \ln (1/(1-F(t_i)))$ and $x=\ln t_i$, the linear equation can be created. If the sample data meet the Weibull distribution, $y=\ln \ln (1/(1-F(t_i)))$ and lnt_i are linear and the observed value of parameters m and η can be calculated by Equation (10).

$$\{\begin{array}{l}\widehat{m}=b\\ \widehat{\eta }=\exp \left(-\frac{a}{b}\right)\end{array}$$

(10)

2.3.3. Normal Distribution

The probability density function of the normal distribution has two parameters, μ and σ. The accumulative distribution function meets the relation shown in Equation (11) if the function is converted to standard normal distribution.

$$F(t_i)=\Phi \left(\frac{t_i-\mu }{\sigma }\right)=\Phi \left(z_i\right)$$

(11)

The linear equation can be constructed for the normal distribution as shown in Equation (12).

$$t_i=\sigma z_i+\mu$$

(12)

In Equations (11) and (12), z_i is the lower fractile of standard normal distribution and can be calculated by the inverse function of the standard normal distribution. If the sample data meet normal distribution, z_i and t_i are linear and the observed value of parameters μ and σ can be calculated by Equation (13).

$$\{\begin{array}{c}\widehat{\mu }=b\\ \widehat{\sigma }=a\end{array}$$

(13)

2.3.4. Logarithmic Normal Distribution

The probability density function of the logarithmic normal distribution has two parameters, μ and σ. The accumulative distribution function meets the relation as shown in Equation (14) if the function is converted to standard normal distribution.

$$F(\ln t_i)=\Phi \left(\frac{\ln t_i-\mu }{\sigma }\right)=\Phi \left(z_i\right)$$

(14)

The linear equation can be constructed for the logarithmic normal distribution as shown in Equation (15).

$$\ln t_i=\sigma z_i+\mu$$

(15)

If the sample data meet the logarithmic normal distribution, z_i and lnt_i are linear and the observed value of parameters μ and σ can be calculated by Equation (16).

$$\{\begin{array}{c}\widehat{\mu }=b\\ \widehat{\sigma }=a\end{array}$$

(16)

2.3.5. Gamma Distribution

The probability density function of the gamma distribution cannot be constructed as one linear equation, and the parameters α and β can be calculated by the maximum likelihood method. If the data meet the gamma distribution, the likelihood equation can be constructed in Equation (17).

$$L(t_1,t_2,\cdots ,t_k,\alpha ,\beta )={\displaystyle \prod _{i=1}^k\frac{{\beta }^{\alpha }{t}_i^{\alpha -1}{e}^{-\beta t_i}}{\Gamma (\alpha )}}$$

(17)

The execute logarithm of Equations (17) and (18) can be gained. In Equation (18), α and β can be solved by the numerical iteration method.

$$\{\begin{array}{c}\frac{kd(\ln \Gamma (\alpha ))}{dt}-k\ln \beta -{\displaystyle \sum \ln t_i=0}\\ k\alpha \beta -{\beta }^2{\displaystyle \sum \ln t_i=0}\end{array}$$

(18)

2.4. Model Optimization

The reliability assessment results will differ greatly if the reliability models are different. Each subsystem will be fitted by five distribution functions, so that it is necessary to select one optimal model as the reliability model for each subsystem. The K–S hypothesis test method, correlation coefficient method, and gray correlation degree method are the normal model optimization methods [15,16].

The accuracy of the K–S hypothesis test is proportional to the number of reliability data. The correlation coefficient method is used to optimize the models that are linear or can be converted into a linear relationship. The standard gray correlation is mainly to judge the similarity of two models [17,18]. Not only will the similarity be judged, but also the closeness should be calculated between sample data and the fitted model when the model optimization is executed. One modified gray correlation model optimization method is proposed based on the standard gray correlation, which is called the similar slope and close median gray correlation. The basic idea of the model optimization method is to judge the similarity degree of the slope of adjacent points between the sample data and fitted curve and the close degree of the median between the sample data and fitted curve. The algorithm of the model optimization method is shown as follows and the flow chart is shown in Figure 2.

• Calculate the adjacent points’ slope of sample data and fitted curve, as shown in Equation (19).

  $$\{\begin{array}{l}{K}_i=\frac{\widehat{F}(t_{i+1})-\widehat{F}(t_i)}{t_{i+1}-t_i}\hfill \\ K_{ji}=\frac{F_j(t_{i+1})-F_j(t_i)}{t_{i+1}-t_i}\hfill \end{array}$$

  (19)

  where
  • $\widehat{F}(t_i)$ is the function value of the ith sample data,
  • $K_{ji}$ is the slope of the ith and (i+1)th sample data of the jth fitting function, and
  • $F_j(t_i)$ is the function value of the jth fitting function when the independent variable equals to the value of the ith sample data.
• Calculate the adjacent points’ median of sample data and fitted curve, as shown in Equation (20).

  $$\{\begin{array}{l}{V}_i=\frac{\widehat{F}(t_{i+1})+\widehat{F}(t_i)}{2}\hfill \\ V_{ji}=\frac{F_j(t_{i+1})+F_j(t_i)}{2}\hfill \end{array}$$

  (20)
• Calculate the absolute value of difference of slope and median, as shown in Equation (21).

  $$\{\begin{array}{l}D{K}_{ji}=\left|K_i-K_{ji}\right|\hfill \\ D{V}_{ji}=\left|V_i-V_{ji}\right|\hfill \end{array}$$

  (21)
• Maximum image processing of slope and median, as shown in Equation (22).

  $$\{\begin{array}{c}R{K}_{ji}=D{K}_{ji}/\max (D{K}_{ji})\\ R{V}_{ji}=D{V}_{ji}/\max (D{V}_{ji})\end{array}$$

  (22)
• Calculate the gray correlation between sample data and fitted function, as shown in Equation (23).

  $$R_{kvj}=\frac{1}{n-1}{\displaystyle \sum _{i=1}^{n-1}R{K}_{ji}}\frac{1}{n-1}{\displaystyle \sum _{i=1}^{n-1}R{V}_{ji}}$$

  (23)
• Normalization. In Equation (23), R_kvj is the similarity and closeness between the jth fitted curve and the sample data. The smaller the value of R_kvj, the better the fitting. Usually, the big gray correlation degree indicates the good fitting, and its value is between 0 and 1, which needs to be normalized, as shown in Equation (24).

  $$R_{gj}=\frac{\min (R_{kvj})}{R_{kvj}+\rho \min (R_{kvj})}$$

  (24)

In Equation (24), ρ is the discrimination adjustment coefficient, which is between [0,1]. The smaller ρ is, the greater the degree of distinction will be. The gray correlation can be calculated using the five distribution functions. The distribution function of the maximum value of the gray correlation will be selected as the reliability model of the corresponding subsystem.

3. Reliability Evaluation Method

Although the reliability model of each subsystem of the CNC grinding machine tool can be done using the method in Section 2, the reliability of each subsystem can be evaluated by the model and then the system reliability can be gained by the subsystem’s reliability. In fact, the time when each subsystem breaks down is random and the MTBF (mean time between failures) of each subsystem also changes. The Monte Carlo method can simulate the randomness well, thus the Monte Carlo simulation is used to evaluate the whole machine’s reliability of the CNC grinding machine tool in this paper.

3.1. Monte Carlo Simulation

Monte Carlo is also known as the statistical test method, stochastic simulation method, and random sampling method, which is one method for studying distribution characteristics by repeatedly generating time series to calculate the estimated parameters and statistics [19,20].

The frequency of events or arithmetic mean of random variable X is regarded as the solution of the problem by the Monte Carlo simulation method. Suppose that the samples of the random variable X are as follows: X₁, X₂, …, X_N, the arithmetic mean of the random variable X is shown in Equation (25).

$$\overline{X}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{X}_i}$$

(25)

Equation (26) can be gained by the strong law of large number, in which the ε is any small positive. From Equation (26), when N is big enough, $\overline{X}$ converges to E(X), which is the convergence guarantee of the Monte Carlo simulation method [21,22].

$$\underset{N\to \infty }{\lim }P\left\{\left|\overline{X}-E(X)\right|<\epsilon \right\}=1$$

(26)

Equation (27) can be gained by the central limit theorem, in which the μ_α is any value.

$$P\left\{\left|\overline{X}-E(X)\right|<\frac{{\mu }_{\alpha }\sigma }{\sqrt{N}}\right\}\approx \frac{2}{\sqrt{2\pi }}{\displaystyle {\int }_0^{u_{\alpha }}\exp \left(t^2/2\right)}dt=1-\alpha$$

(27)

where

• α is the significant level,
• σ is the standard deviation of the random variable X, and
• μ_α is the quantile of the standard normal distribution.

It is necessary to construct one probability statistics model, define the random variable, sample based on the known distribution model, generate random data, and calculate when using Monte Carlo method. The accuracy of the Monte Carlo method is related to the number of samples—the larger the number of samples, the smaller the error [23].

3.2. Random Data Generation

The distribution of time between failures of each subsystem of the CNC grinding machine tool may meet the exponential distribution, Weibull distribution, normal distribution, lognormal distribution, or gamma distribution. The random data generation method is put forward as below.

If the distribution function of random variable X is F(x), which is continuous, F(x) is a uniform distribution of random variables on the [0,1]. In order to obtain the random data that meet distribution function of F(x), the random data can be solved by the uniform distribution of r on the [0,1], as shown in Equation (28).

$$r=F(x)$$

(28)

In Equation (28), x is the random data of distribution function F(x). The random data that meet the exponential distribution, Weibull distribution, normal distribution, lognormal distribution, and gamma distribution can be calculated by Equation (28), as shown in Equations (29) to (33).

$$x=-\frac{1}{\lambda }\ln r$$

(29)

$$x=\eta {\left(-\ln r\right)}^{1/\beta }$$

(30)

$$x=\mu +\sigma \sqrt{-2\ln r_1}\cos (2\pi r_2)$$

(31)

$$x=e^{\mu +\sigma \sqrt{-2\ln r_1}\cos (2\pi r_2)}$$

(32)

$$x=-b\ln \left({\displaystyle \prod _{i=1}^{round(a)}{r}_i}\right)$$

(33)

3.3. Reliability Evaluation Algorithm

1. Work Time Calculation

Assuming the average life cycle of the CNC grinding machine tool is T_L years, the average annual maintenance time of the life cycle is T_M, the annual average normal downtime is T_S, and then the normal working time in the life cycle of the CNC grinding machine T_W is as shown in Equation (34).

$$T_W=\left(365\times 24-T_M-T_S\right)\times T_L$$

(34)

2. Quantity of Random Data Calculation

The quantity of generated random data of time between failures of each subsystem of each CNC grinder can be calculated by Equation (35). In Equation (35), i is the number of the subsystem (i=1, 2, …, n), n is the amount of the subsystem, and MTBF_i is the MTBF of the ith subsystem.

$$k_i=\frac{T_W}{MTB{F}_i}$$

(35)

3. Dimension of Random Data Calculation

To enhance the accuracy, m CNC grinders are selected for simulation. The dimension of random data d_i generated by the ith subsystem can be calculated by Equation (36).

$$d_i=m\times k_i$$

(36)

4. Random Data Generation

After calculating the distribution type and parameters of distribution function of each subsystem, the random data of time between failures of each subsystem can be generated according to Equations (29) to (33). The random data matrix T_i of the ith subsystem is shown in Equation (37).

$${\mathit{T}}_i={\left[\begin{array}{cccc}{T}_{00}^i& T_{01}^i& \cdots & T_{0k_i}^i\\ T_{10}^i& T_{11}^i& \cdots & T_{1k_i}^i\\ ⋮& ⋮& \ddots & ⋮\\ T_{m0}^i& T_{m1}^i& \cdots & T_{m{k}_i}^i\end{array}\right]}_{(m\times k_i)}$$

(37)

5. Sum of Every Time Between Failures

After all subsystems’ random data are generated, the sum of every time between failures can be calculated by Equation (38).

$$T_{sum}={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{u=1}^m{\displaystyle \sum _{v=1}^{k_i}{T}_{uv}^i}}}$$

(38)

where k_i is the amount of random data of the ith subsystem.

6. Sum of Fault Amount Calculation

It is necessary to calculate the sum of fault amount of each subsystem and each CNC grinding machine in the life cycle, as shown in Equation (39).

$$n_{sum}=m{\displaystyle \sum _{i=1}^n{k}_i}$$

(39)

7. System MTBF Calculation

The system reliability of $MTB{F}_s^m$ can be calculated by the Monte Carlo simulation method, as shown in Equation (40).

$$MTB{F}_s^m=\frac{T_{sum}}{n_{sum}}=\frac{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{u=1}^m{\displaystyle \sum _{v=1}^{k_i}{T}_{uv}^i}}}}{m{\displaystyle \sum _{j=1}^n{k}_j}}$$

(40)

Taking into account the monotonicity of different distribution functions, the interval estimation of system reliability of the CNC grinding machine can be calculated by replacing the point estimation value with the upper and lower bound of interval estimate value to generate random data in step 4.

4. Case Study

In order to illustrate the application of the reliability model optimization of the subsystems and the Monte Carlo reliability evaluation method, a CNC cylindrical grinding machine is used as a research case. The CNC cylindrical grinding machine is used to grind the shaft parts. The feed precision is 0.001 mm, the roundness of the ground parts is 0.002 mm, and the grinding line speed is 60 m/s of the studied CNC cylindrical grinding machine. The CNC cylindrical grinding machine can be divided into 10 subsystems according to their structural characteristics, as shown in

Table 2. Reliability models and parameters of subsystems. CNC—computer numerical control; MTBF—mean time between failures.

Subsystem	Distribution Type	Parameters
base	exponential	λ = 6.61 × 10–5
CNC	gamma	a = 6.81 × 10–1, b = 9.41 × 103
spindle	gamma	a = 7.81 × 10–1, b = 9.68 × 103
feeder	gamma	a = 1.539, b = 1.31 × 103
electrical	Weibull	β = 3.84 × 10–1, η = 6.58 × 102
hydraulic	gamma	a = 7.57 × 10–1, b = 1.36 × 104
cooler	lognormal	μl = 7.011, σl = 1.644
lubrication	gamma	a = 6.05 × 10–1, b = 1.26 × 104
header	Weibull	β = 5.62 × 10–1, η = 1.65 × 103
gauge	gamma	a = 8.44 × 10–1, b = 9.25 × 103

.

4.1. Modeling of Subsystem

Fifteen CNC grinding machines were tracked for three years and nine months and 748 failure data were collected. The distribution type and probability density function are solved by data grouping, model optimization by five distribution functions of each subsystem, as shown in Table 2 and the cumulative distribution curve of each subsystem is shown in Figure 3.

4.2. System Reliability Evaluation

In order to analyze and compare easily, the system reliability evaluated by the observed value and by the whole fitting method is also listed below.

4.2.1. Observed Value

● Point estimation

Suppose that the observed value of system reliability is MTBF_s^o, the amount of CNC grinding machine is n_m, the year of failure data collecting is y_r, the day of failure data collecting each year is d_r, the work time each day is h_r, the amount of failures is n_f, and the mean maintenance time is t_ma, the observed value of system reliability can be calculated by Equation (41).

$$MTB{F}_s^o=\frac{n_m·y_r·d_r·h_r-n_f·t_{ma}}{n_f}$$

(41)

The observed value of system reliability is 563 h on condition that the work time each day is 24 h and the mean maintenance time is 2 h.

● Interval estimation

The interval estimation of system reliability of the CNC grinding machine tool can be calculated by the confidence coefficient, as shown in Equation (42).

$$\left[MTB{F}_s{}^o·C_L,MTB{F}_s{}^o·C_U\right]$$

(42)

where

• MTBF_s^o is the observed value of system reliability of the CNC grinding machine,
• C_L is the lower confidence coefficient, and
• C_U is the upper confidence coefficient.

The interval estimation of system reliability of the CNC grinding machine can be calculated by the confidence coefficient table and the interval is [415,782] h.

4.2.2. Whole Fitting Method

At present, many scholars regard the CNC grinding machine as one whole, and the system reliability is evaluated directly by all the failure data. It is one acceptable reliability evaluation method if the failure data are not enough. For comparison, the system reliability is also evaluated by the whole fitting method.

If the CNC grinding machine tool is regarded as a whole, all the failure data belong to the whole grinding machine, and the probability density function of the whole machine can be fitted by the method in Section 2, as shown below. Its probability density curve and cumulative distribution curve are shown in Figure 4 and Figure 5, respectively. The distribution type of the system reliability model of the CNC grinding machine is gamma distribution and the parameter a is 0.663 and b is 689.8.

The MTBF of the gamma distribution can be solved by its probability density function, as shown in Equation (43). The system reliability of the CNC grinding machine can be calculated, and its point estimation is 457 h and interval estimation is [370, 564] h.

$$MTB{F}_g={\displaystyle {\int }_0^{\infty }t{f}_g(t)dt}=ab$$

(43)

4.2.3. Monte Carlo Simulation

The accuracy of the system reliability evaluation of the Monte Carlo simulation is determined by the simulation time and amount of CNC grinding machine. The evaluation result of different simulation times and different amounts of CNC grinding machine by the algorithm mentioned in Section 2 is shown in Figure 6.

The result will fluctuate severely from that in Figure 6 when the simulation time and amount of the CNC grinding machine are small, and it will tend to be stable when the simulation time is more than 10 years and the amount of the CNC grinding machine is more than 10, which fluctuates slightly between 530 and 560 h.

The point estimation of system reliability is 551 h on condition that the simulation time is 20 years, the amount of the CNC grinding machine is 20, and the interval estimation is between 511 h and 585 h.

$$MTB{F}_s^{mk}=\frac{T_{sum}}{n_{sum}}=551$$

(44)

4.3. Comparison and Analysis

The results evaluated by the three methods are showed in Figure 7, on condition that the confidence level is 95%.

From Figure 7, it can be found that if all the fault data are regarded as a whole to fit, the point estimation of MTBF will be less than MTBF of the observed value. The main reason is that the failure data are too focused on the early time of the reliability test. The evaluation result by the Monte Carlo method is close to the observed value. The interval estimation of Monte Carlo is the least of the three methods, that is to say that the evaluation result is in one smaller interval below a certain confidence level than the other two methods. The smaller the interval estimation range, the bigger the reference to engineering. It can be concluded that the accuracy of the reliability evaluation of the Monte Carlo method is high and it has important reference engineering significance to the reliability design.

5. Conclusions

This paper presented the reliability evaluation method of complex electromechanical products, and illustrated the application of the method to the CNC cylindrical grinding machine. This work led to the following conclusions.

The traditional method of fitting the whole machine and then carrying out the reliability evaluation can not reveal the failure law of each subsystem. The purpose of the reliability evaluation is to improve the reliability, and the system reliability enhancement is determined by the subsystems’ reliability. Compared with the whole machine fitting, the reliability modeling of subsystems has more engineering significance. The reliability modeling and optimization methods of subsystems are proposed by the commonly distribution functions.

The failure time of each subsystem does not strictly follow the reliability model, rather it is random, and Monte Carlo can simulate this randomness very well. The paper proposed one system reliability evaluation method based on Monte Carlo simulation; using this method to evaluate the system reliability is closer to reality.

Through comparative analysis, it is found that the length of the reliability estimation interval evaluated by the Monte Carlo simulation method is 8.2% and 15.5% of that evaluated directly by the field data and evaluated by the whole machine evaluation method, respectively. For engineering, the shorter the interval length, the more practical it is.

The system reliability evaluation method of subsystem reliability modeling and Monte Carlo simulation can also be extended to other complex electromechanical equipment when the field data are limited.