The Influence of Laser Linewidth on the Brillouin Shift Frequency Accuracy of BOTDR
Abstract
:Featured Application
Abstract
1. Introduction
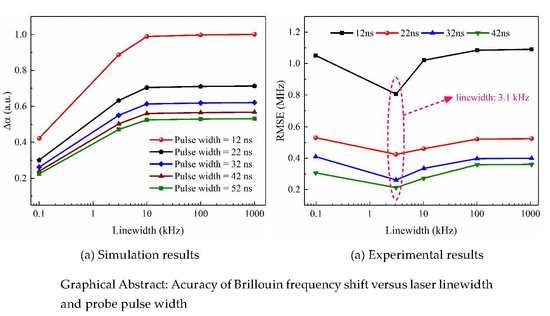
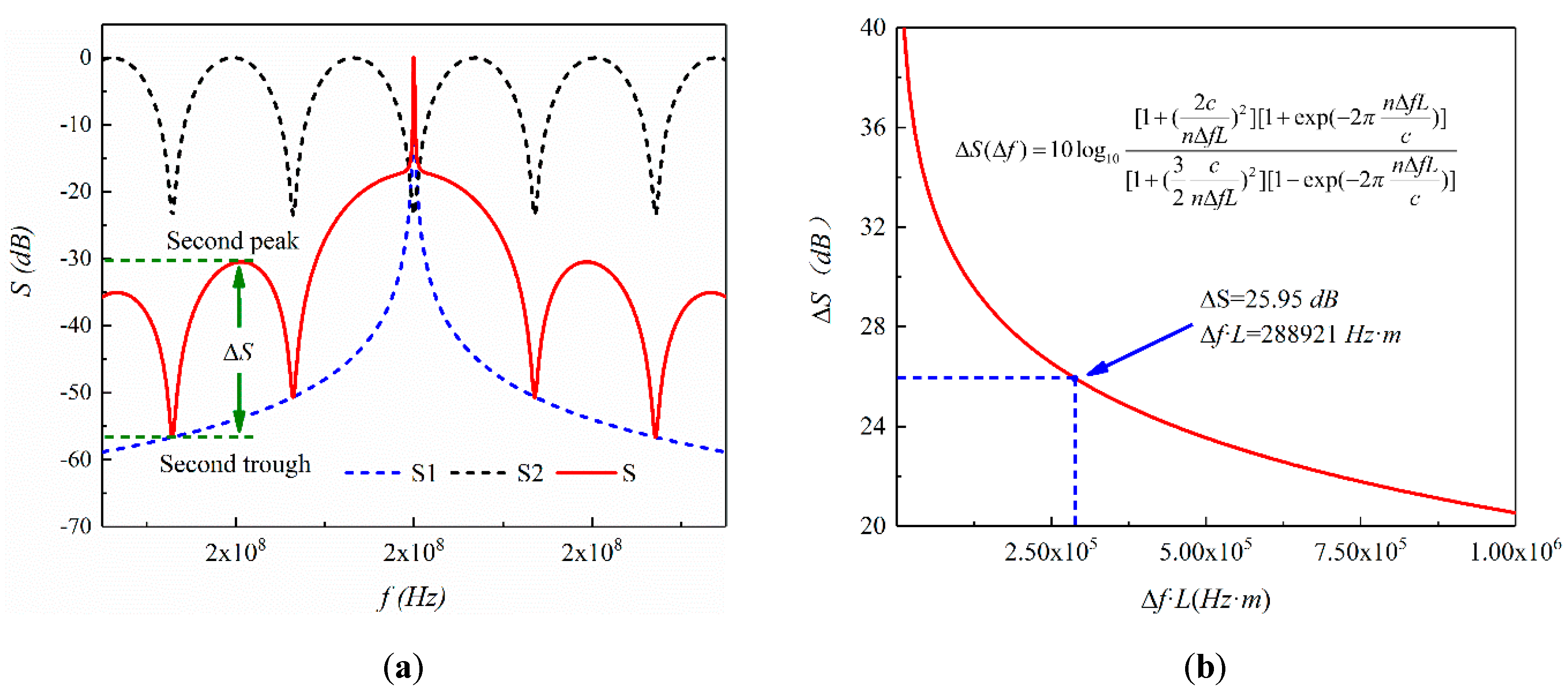
2. Numerical Simulation
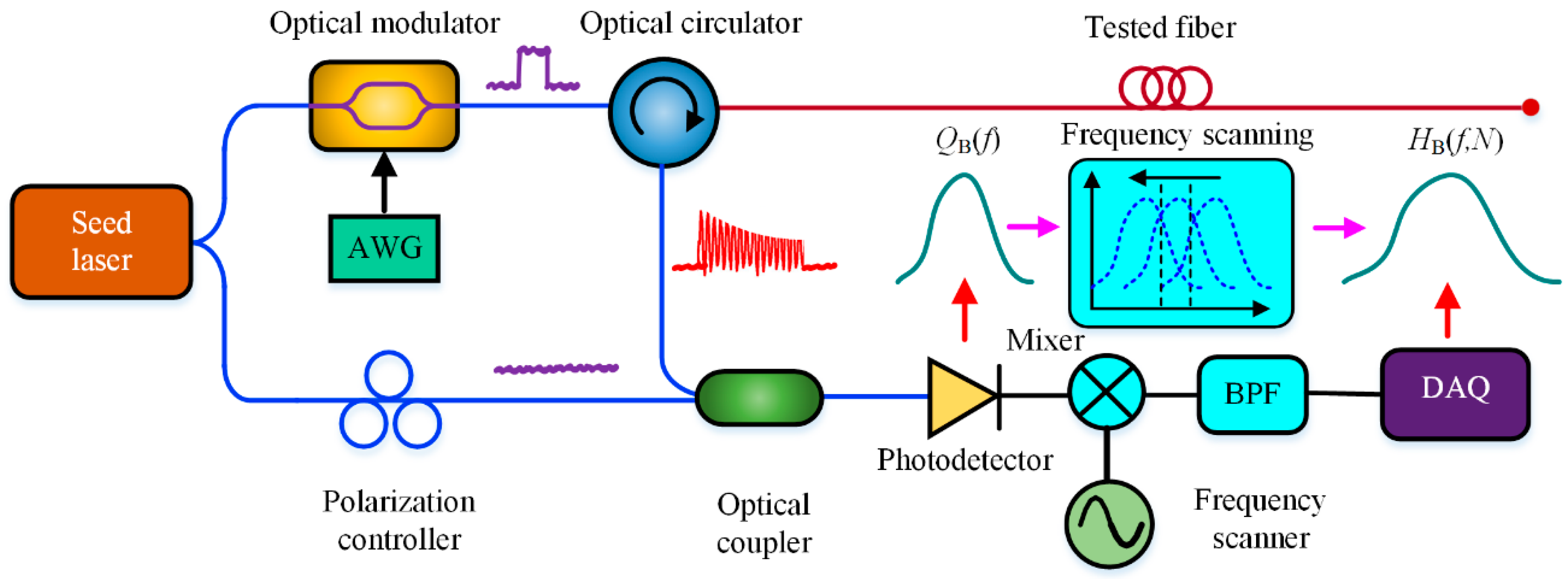
3. Experiment Setup
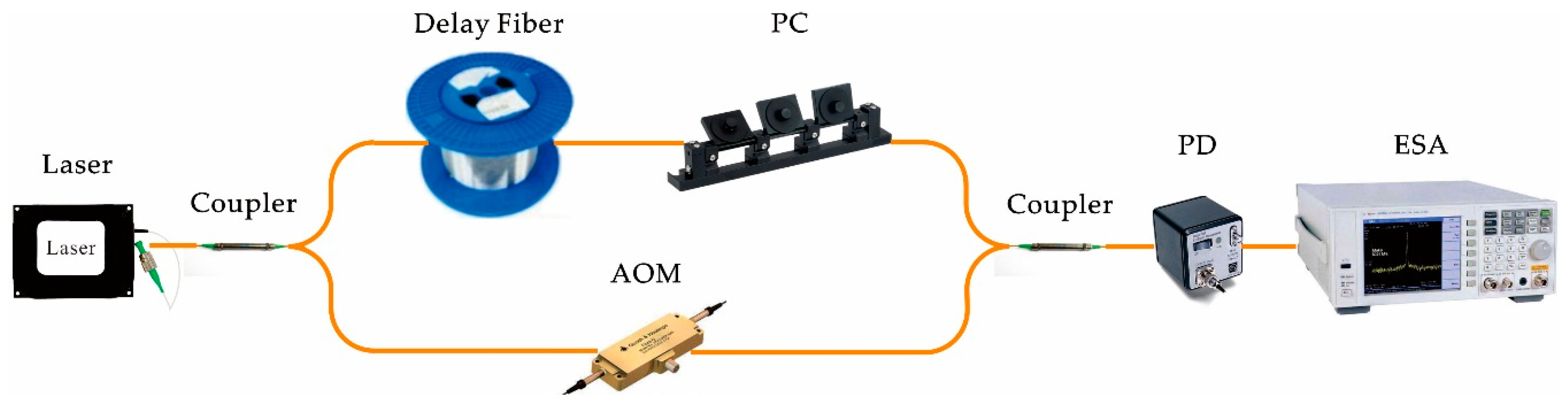
3.1. Experiment Setup for Measuring Laser Linewidth
3.2. FS-BOTDR Setup for Measuring BFS
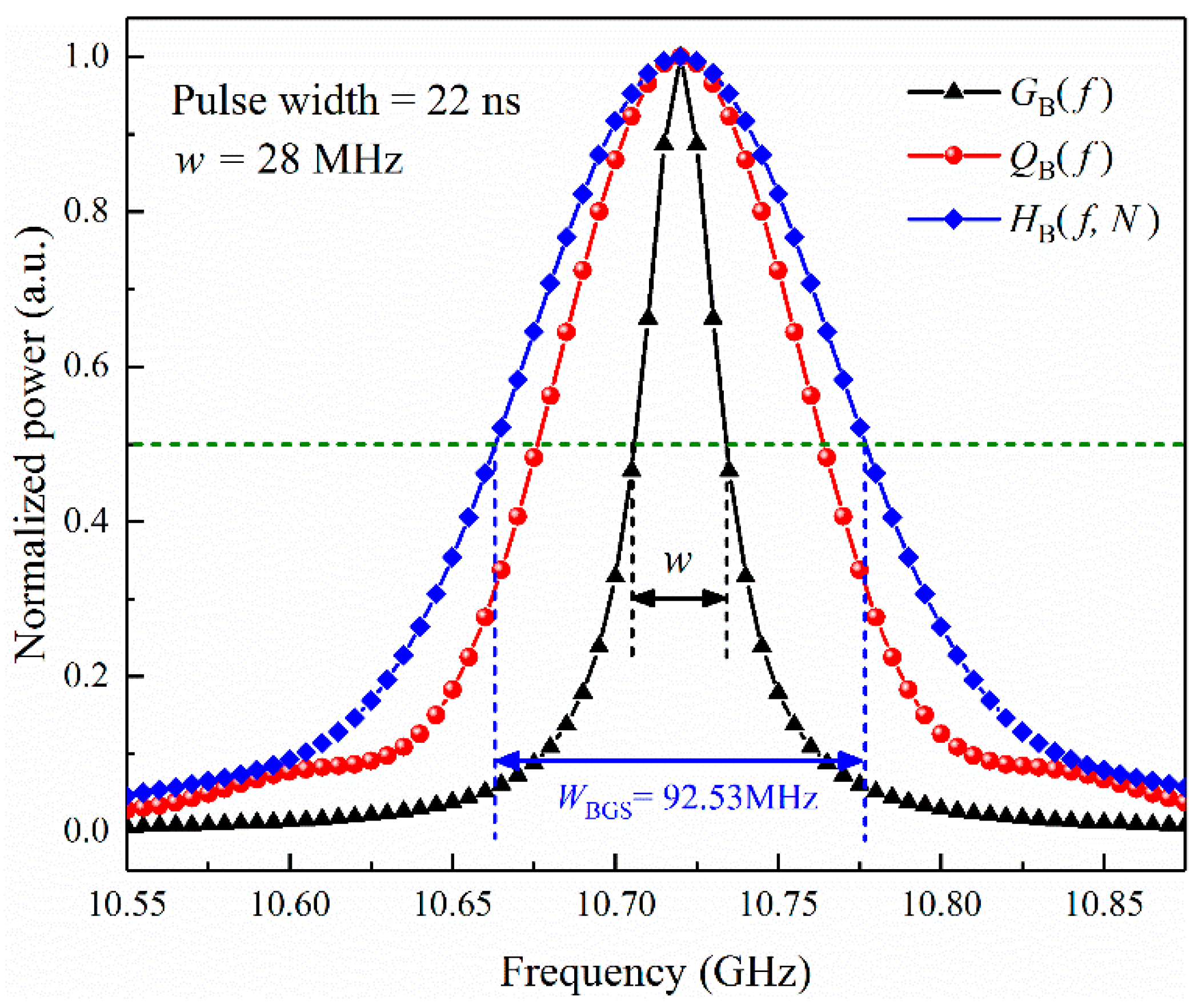
4. Experiment Results and Discussions
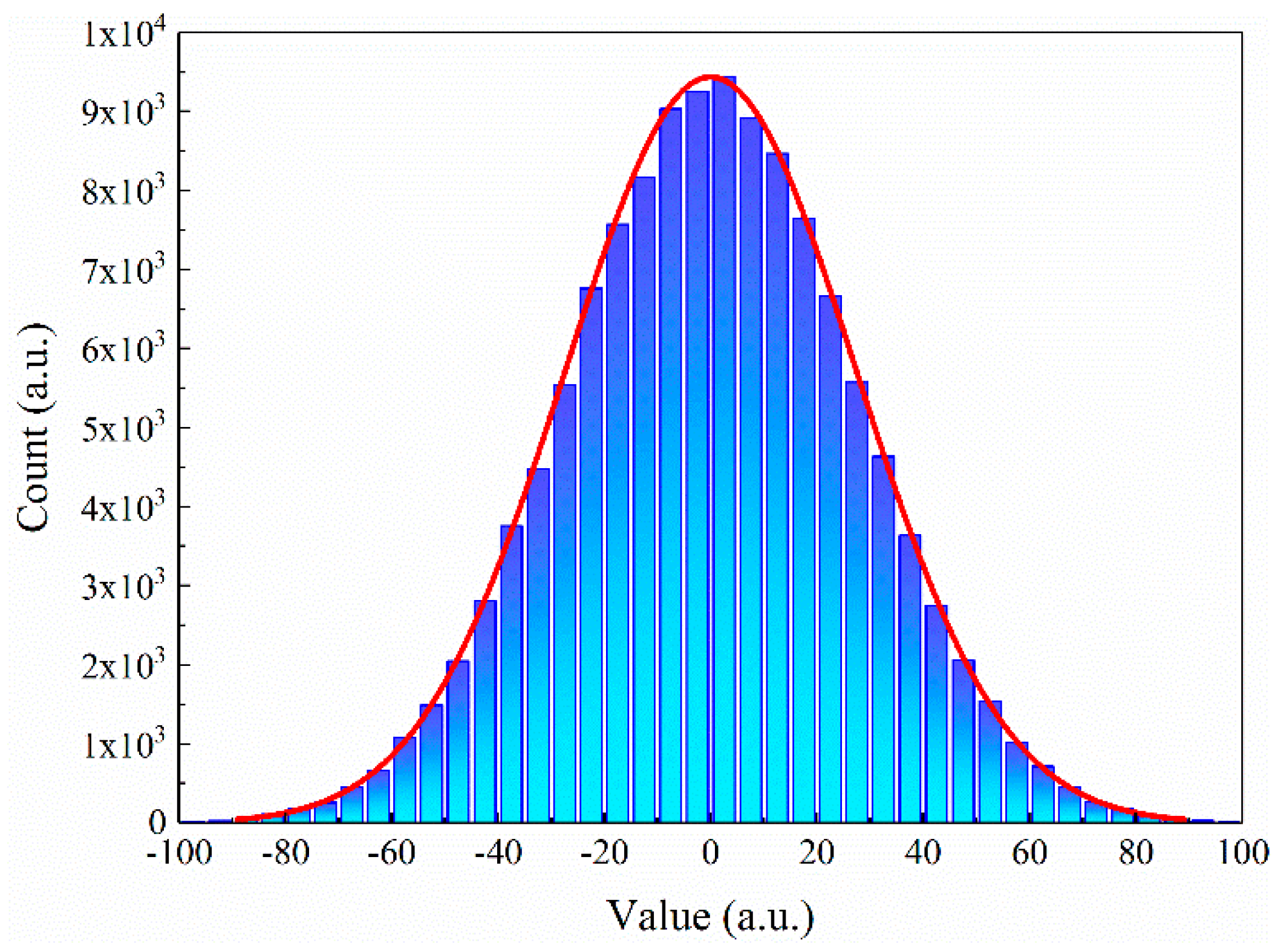
4.1. Measurement of Laser Linewidth
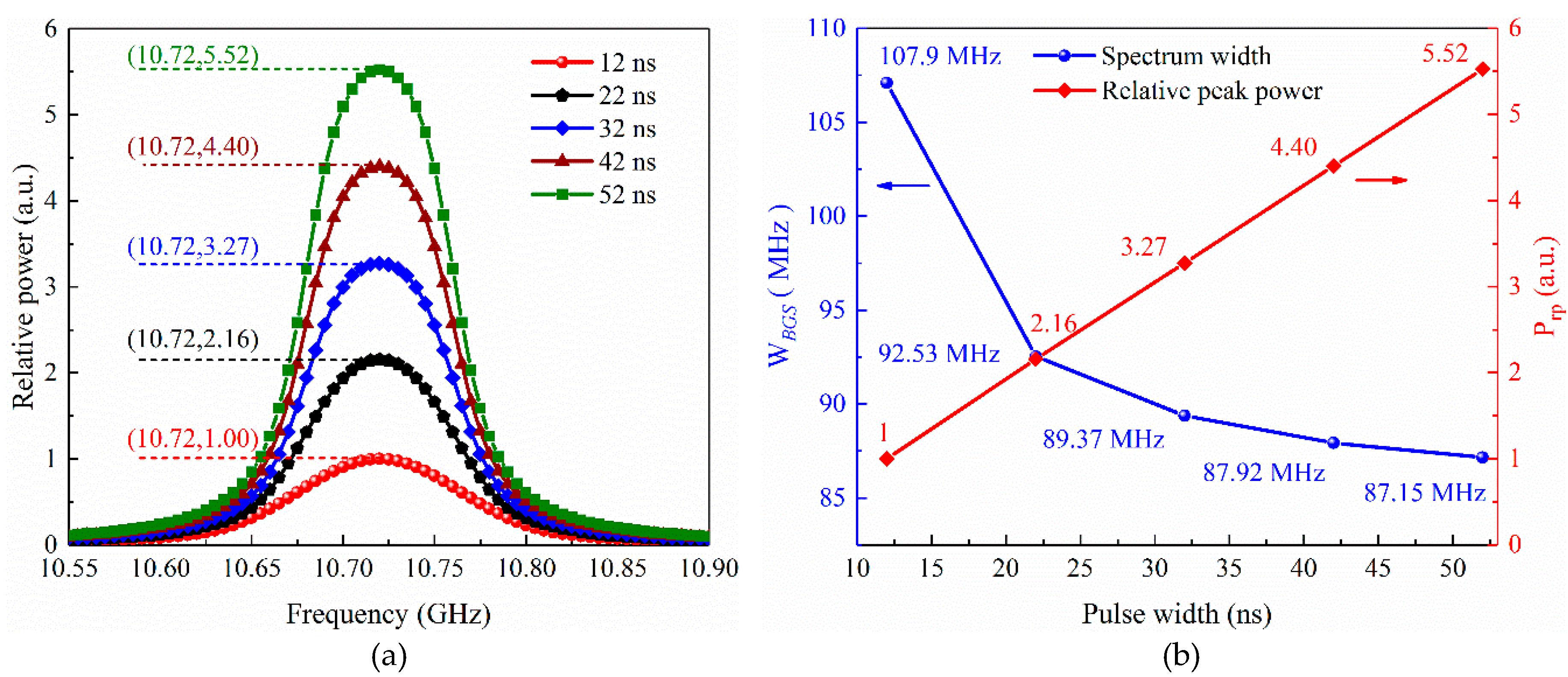
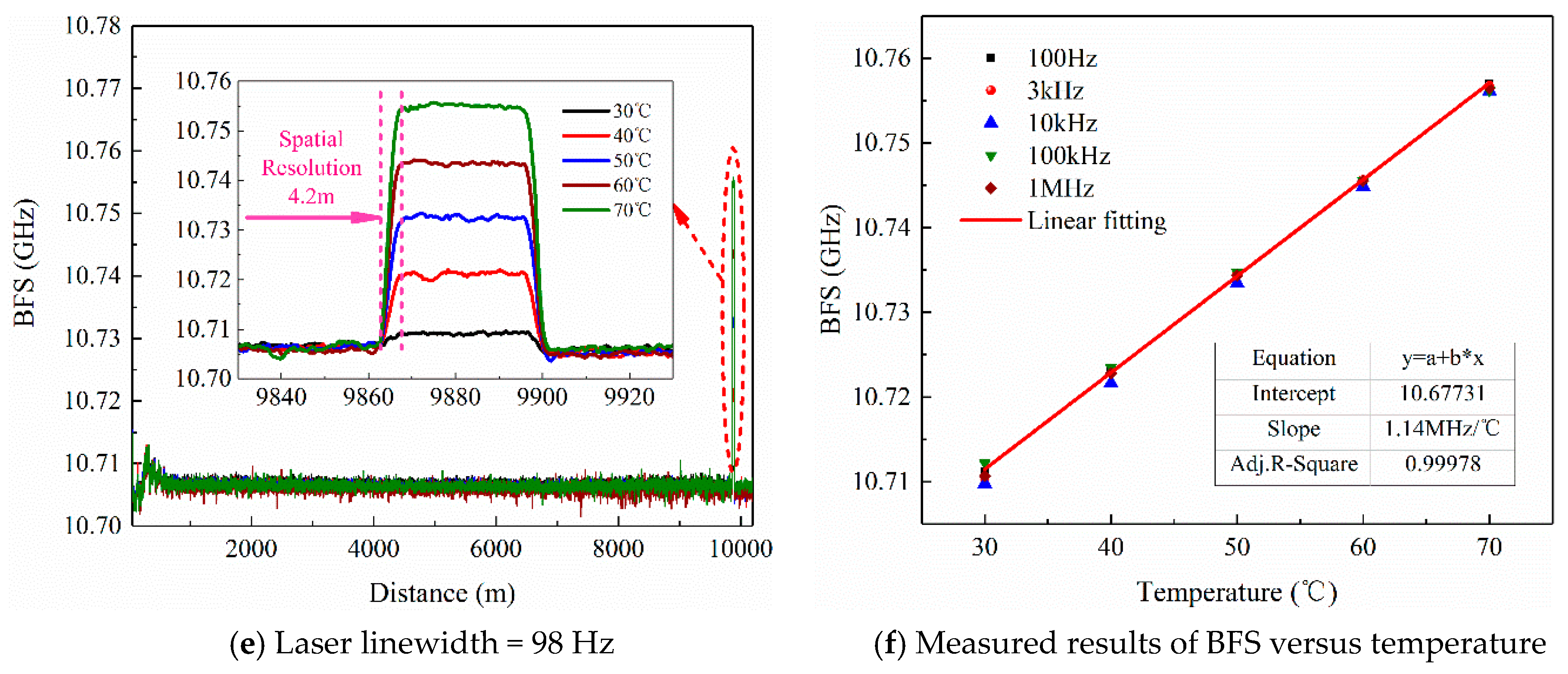
4.2. BFS Distribution Measurement
4.3. BGS Width Evaluation
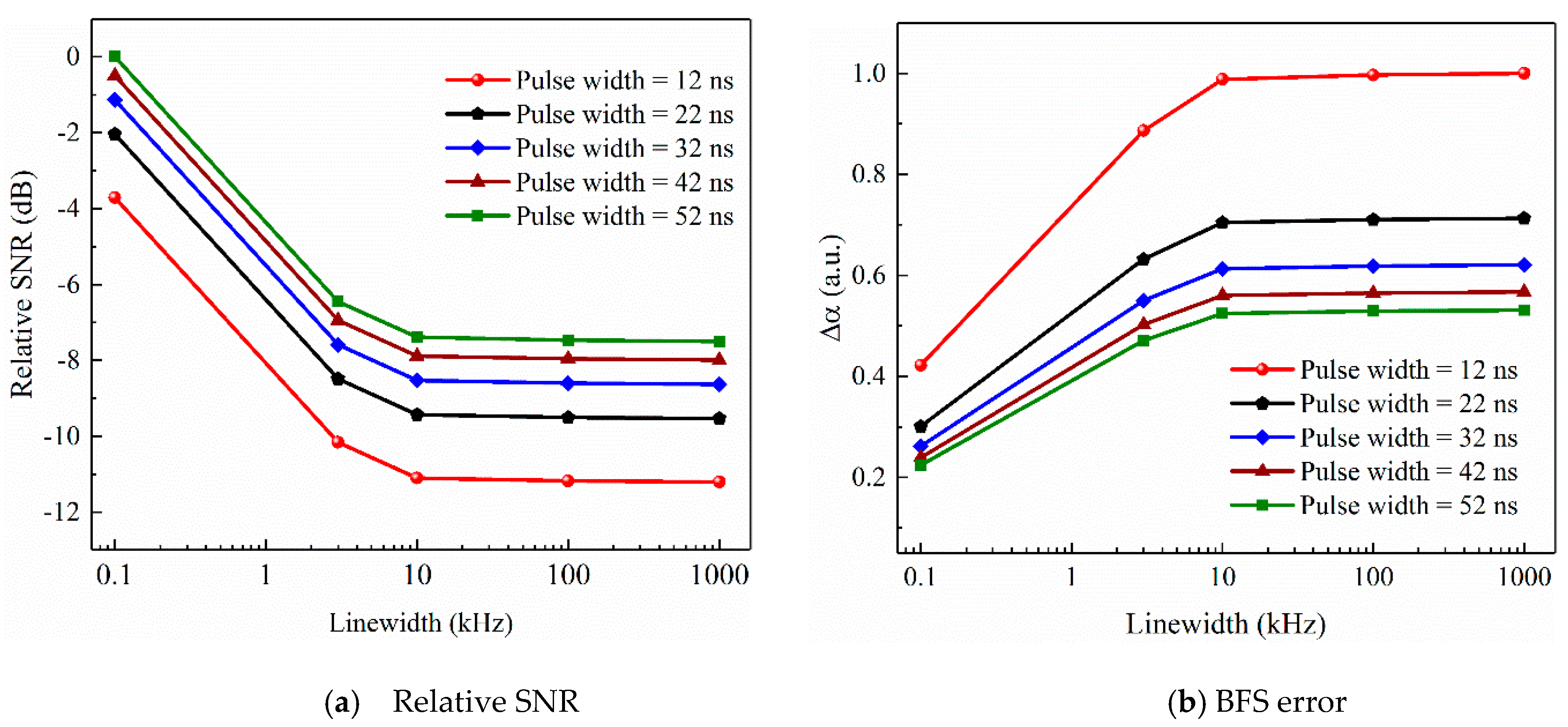
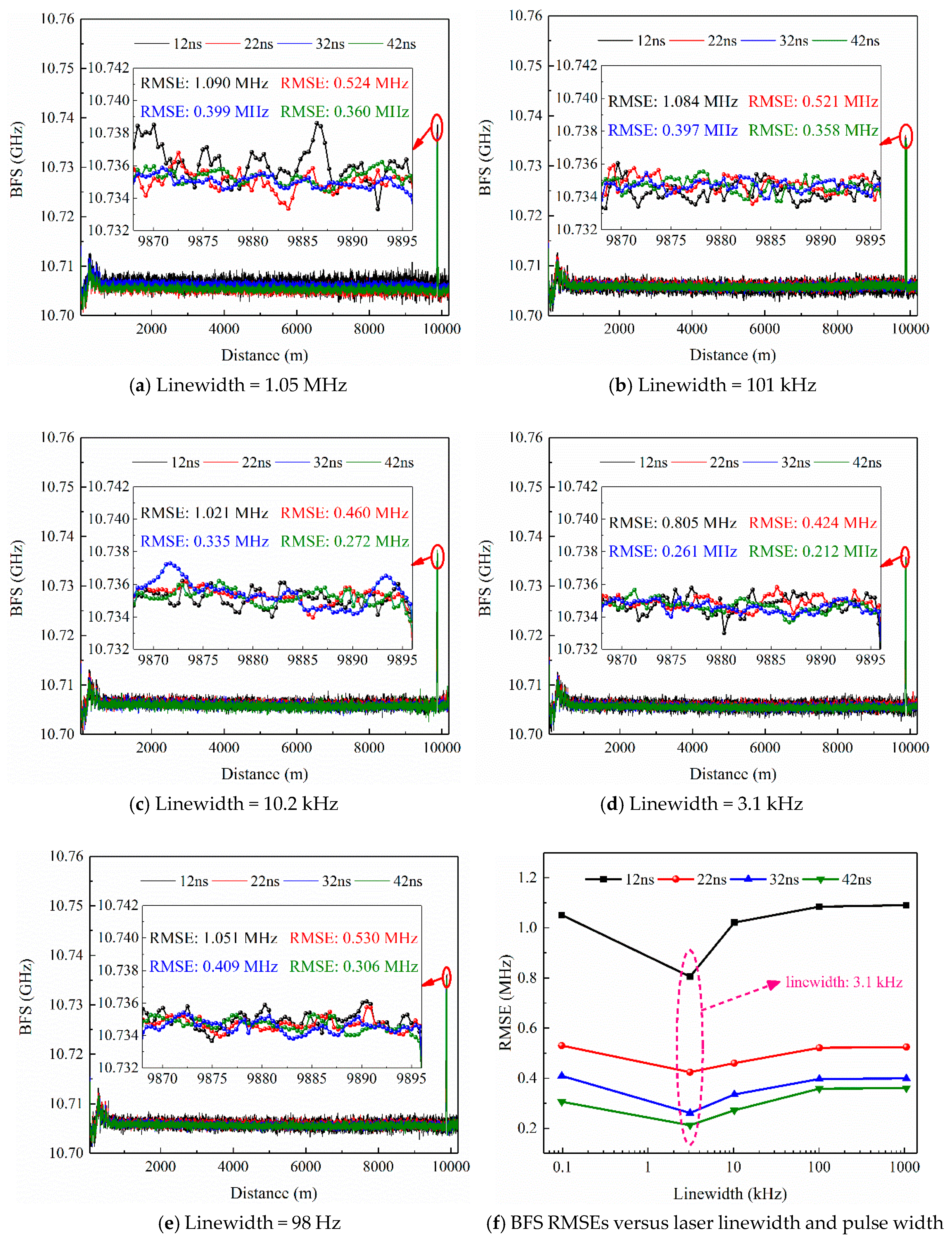
4.4. BFS Accuracy Evaluation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| BGS width for continuous light | w | 28 | MHz |
| Brillouin frequency shift | fB | 10.7 | GHz |
| Startting frequecy for scanning frequency | fs | 10.4 | GHz |
| Frequency step | fstep | 1 | MHz |
| Number of frequency-scanning points | N | 671 | ------ |
| Bandwidth of the BPF | B | 87 | MHz |
| Speed of light in vacuum | c | 3×108 | m/s |
| Refractive index | n | 1.5 | ------ |
| Pulse width | τ | 12, 22, 32, 42, 52 | ns |
| Laser linewidth | Δf | 100, 3000, 10,000, 100,000, 1,050,000 | Hz |
| Optical path difference | ΔL | 20 | km |
Appendix B
References
- Kurashima, T.; Horiguchi, T.; Izumita, H.; Furukawa, S.; Koyamada, Y. Brillouin optical-fiber time domain reflectometry. IEICE Trans. Commun. 1993, E76-B, 382–390. [Google Scholar]
- Geng, J.; Staines, S.; Blake, M.; Jiang, S. Distributed fiber temperature and strain sensor using coherent radio-frequency detection of spontaneous Brillouin scattering. Appl Opt. 2007, 46, 5928–5932. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Wang, Y.; Hu, Q.; Che, D.; Chen, X.; Shieh, W. Measurement of distributed mode coupling in a few-mode fiber using a reconfigurable Brillouin OTDR. Opt. Lett. 2014, 39, 6418–6421. [Google Scholar] [CrossRef] [PubMed]
- Hong, C.; Zhang, Y.; Li, G.; Zhang, M.; Liu, Z. Recent progress of using Brillouin distributed fiber optic sensors for geotechnical health monitoring. Sens. Actuators A 2017, 258, 131–145. [Google Scholar] [CrossRef]
- Soto, M.A.; Bolognini, G.; Di Pasquale, F. Enhanced simultaneous distributed strain and temperature fiber sensor employing spontaneous Brillouin scattering and optical pulse coding. IEEE Photonic Technol. Lett. 2009, 21, 450–452. [Google Scholar] [CrossRef]
- Kim, S.; Kwon, H.; Yang, I.; Lee, S.; Kim, J.; Kang, S. Performance of a distributed simultaneous strain and temperature sensor based on a Fabry-Perot laser diode and a dual-stage FBG optical demultiplexer. Sensors 2013, 13, 15452–15464. [Google Scholar] [CrossRef] [PubMed]
- Webb, G.T.; Vardanega, P.J.; Hoult, N.A.; Fidler, P.R.A.; Bennett, P.J.; Middleton, C.R. Analysis of fiber-optic strain-monitoring data from a prestressed concrete bridge. J. Bridge Eng. 2017, 22, 05017002. [Google Scholar] [CrossRef]
- Moffat, R.; Sotomayor, J.; Beltrán, J.F. Estimating tunnel wall displacements using a simple sensor based on a brillouin optical time domain reflectometer apparatus. Int. J. Rock Mech. Min. Sci. 2015, 75, 233–243. [Google Scholar] [CrossRef]
- Hao, Y.; Cao, Y.; Ye, Q.; Cai, H.; Qu, R. On-line temperature monitoring in power transmission lines based on Brillouin optical time domain reflectometry. Optik 2015, 126, 2180–2183. [Google Scholar] [CrossRef]
- Naruse, H.; Uehara, H.; Deguchi, T.; Fujihashi, K.; Onishi, M.; Espinoza, R.; Guzman, C.; Pardo, C.; Ortega, C.; Pinto, M. Application of a distributed fibre optic strain sensing system to monitoring changes in the state of an underground mine. Meas. Sci. Technol. 2007, 18, 3202–3210. [Google Scholar] [CrossRef]
- Maughan, S.M.; Kee, H.H.; Newson, T.P. 57-km single-ended spontaneous Brillouin-based distributed fiber temperature sensor using microwave coherent detection. Opt. Lett. 2001, 26, 331–333. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Lu, Y.; Zhang, X.; Wang, F.; Wang, R. Reducing trade-off between spatial resolution and frequency accuracy in BOTDR using Cohen's Class signal processing method. IEEE Photonic Technol. Lett. 2012, 24, 1337–1339. [Google Scholar] [CrossRef]
- Wang, F.; Zhan, W.; Lu, Y.; Yan, Z.; Zhang, X. Determining the change of Brillouin frequency shift by using the similarity matching method. J. Lightwave Technol. 2015, 33, 4101–4108. [Google Scholar] [CrossRef]
- Zheng, H.; Fang, Z.; Wang, Z.; Lu, B.; Cao, Y.; Ye, Q.; Qu, R.; Cai, H. Brillouin frequency shift of fiber distributed sensors extracted from noisy signals by quadratic fitting. Sensors 2018, 18, 409. [Google Scholar] [CrossRef] [PubMed]
- Hao, Y.; Ye, Q.; Pan, Z.; Cai, H.; Qu, R. Analysis of spontaneous Brillouin scattering spectrum for different modulated pulse shape. Optik 2013, 124, 2417–2420. [Google Scholar] [CrossRef]
- Hao, Y.; Ye, Q.; Pan, Z.; Cai, H.; Qu, R.; Yang, Z. Effects of modulated pulse format on spontaneous Brillouin scattering spectrum and BOTDR sensing system. Opt. Laser Technol. 2013, 46, 37–41. [Google Scholar] [CrossRef]
- Wang, F.; Zhu, C.; Cao, C.; Zhang, X. Enhancing the performance of BOTDR based on the combination of FFT technique and complementary coding. Opt. Express 2017, 25, 3504–3513. [Google Scholar] [CrossRef]
- Hao, Y.; Ye, Q.; Pan, Z.; Cai, H.; Qu, R. Digital coherent detection research on Brillouin optical time domain reflectometry with simplex pulse codes. Chin. Phys. B 2014, 23. [Google Scholar] [CrossRef]
- Lu, Y.; Yao, Y.; Zhao, X.; Wang, F.; Zhang, X. Influence of non-perfect extinction ratio of electro-optic modulator on signal-to-noise ratio of BOTDR. Opt. Commun. 2013, 297, 48–54. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, X.; Ying, Z.; Zhang, X. Performance improvement for long-range BOTDR sensing system based on high extinction ratio modulator. Electron. Lett 2014, 50, 1014–1016. [Google Scholar] [CrossRef]
- Lalam, N.; Ng, W.P.; Dai, X.; Wu, Q.; Fu, Y.Q. Performance improvement of Brillouin ring laser based BOTDR system employing a wavelength diversity technique. J. Lightwave Technol. 2018, 36, 1084–1090. [Google Scholar] [CrossRef]
- Li, C.; Lu, Y.; Zhang, X.; Wang, F. SNR enhancement in Brillouin optical time domain reflectometer using multi-wavelength coherent detection. Electron. Lett 2012, 48, 1139–1141. [Google Scholar] [CrossRef]
- Hao, Y.; Ye, Q.; Pan, Z.; Cai, H.; Qu, R. Influence of laser linewidth on performance of Brillouin optical time domain reflectometry. Chin. Phys. B 2013, 22. [Google Scholar] [CrossRef]
- Naruse, H.; Tateda, M. Trade-off between the spatial and the frequency resolutions in measuring the power spectrum of the Brillouin backscattered light in an optical fiber. Appl. Opt. 1999, 38, 6516–6521. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Zhao, C.; Zhang, H.; Yang, S.; Zhang, D.; Yang, H.; Liu, J. Phase noise reduction by using dual-frequency laser in coherent detection. Opt. Laser Technol. 2016, 80, 169–175. [Google Scholar] [CrossRef]
- Motil, A.; Bergman, A.; Tur, M. State of the art of Brillouin fiber-optic distributed sensing. Opt. Laser Technol. 2016, 78, 81–103. [Google Scholar] [CrossRef]
- Nikles, M.; Thevenaz, L.; Robert, P.A. Brillouin gain spectrum characterization in single-mode optical fibers. J. Lightwave Technol. 1997, 15, 1842–1851. [Google Scholar] [CrossRef] [Green Version]
- Hui, R.; O'Sullivan, M. Fiber Optic Measurement Techniques; Elsevier Academic Press: Burlington, MA, USA, 2009; pp. 196–199. [Google Scholar]
- Du, Z.; Lu, L.; Wang, B.; Jiang, C. Effect of laser diode phase noise on coherent sensing systems. In Proceedings of the 13th International Conference on Advanced Laser Technologies, Tianjin, China, 3–6 September 2005. [Google Scholar] [CrossRef]
- NKT Photonics. Laser Spectral Linewidth. Available online: http://www.sevensix.co.jp/wordpress/wp-content/uploads/2017/07/Linewidth-Application-Note-Version-1-1-October-2013.pdf (accessed on 9 December 2018).
- Huang, S.; Zhu, T.; Cao, Z.; Liu, M.; Deng, M.; Liu, J.; Li, X. Laser linewidth measurement based on amplitude difference comparison of coherent envelope. IEEE Photonic Technol. Lett. 2016, 28, 759–762. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, M.; Zhang, J.; Liu, Y.; Jin, B.; Bai, Q.; Li, Z. Temperature measurement accuracy enhancement in the Brillouin optical time domain reflectometry system using the sideband of Brillouin gain spectrum demodulation. Acta Phys. Sin. 2016, 65. [Google Scholar] [CrossRef]
- Reshak, A.H.; Shahimin, M.M.; Murad, S.A.Z.; Azizan, S. Simulation of Brillouin and Rayleigh scattering in distributed fibre optic for temperature and strain sensing application. Sens. Actuators A 2013, 190, 191–196. [Google Scholar] [CrossRef]
- De Souza, K. Significance of coherent rayleigh noise in fibre-optic distributed temperature sensing based on spontaneous Brillouin scattering. Meas. Sci. Technol. 2006, 17, 1065–1069. [Google Scholar] [CrossRef]

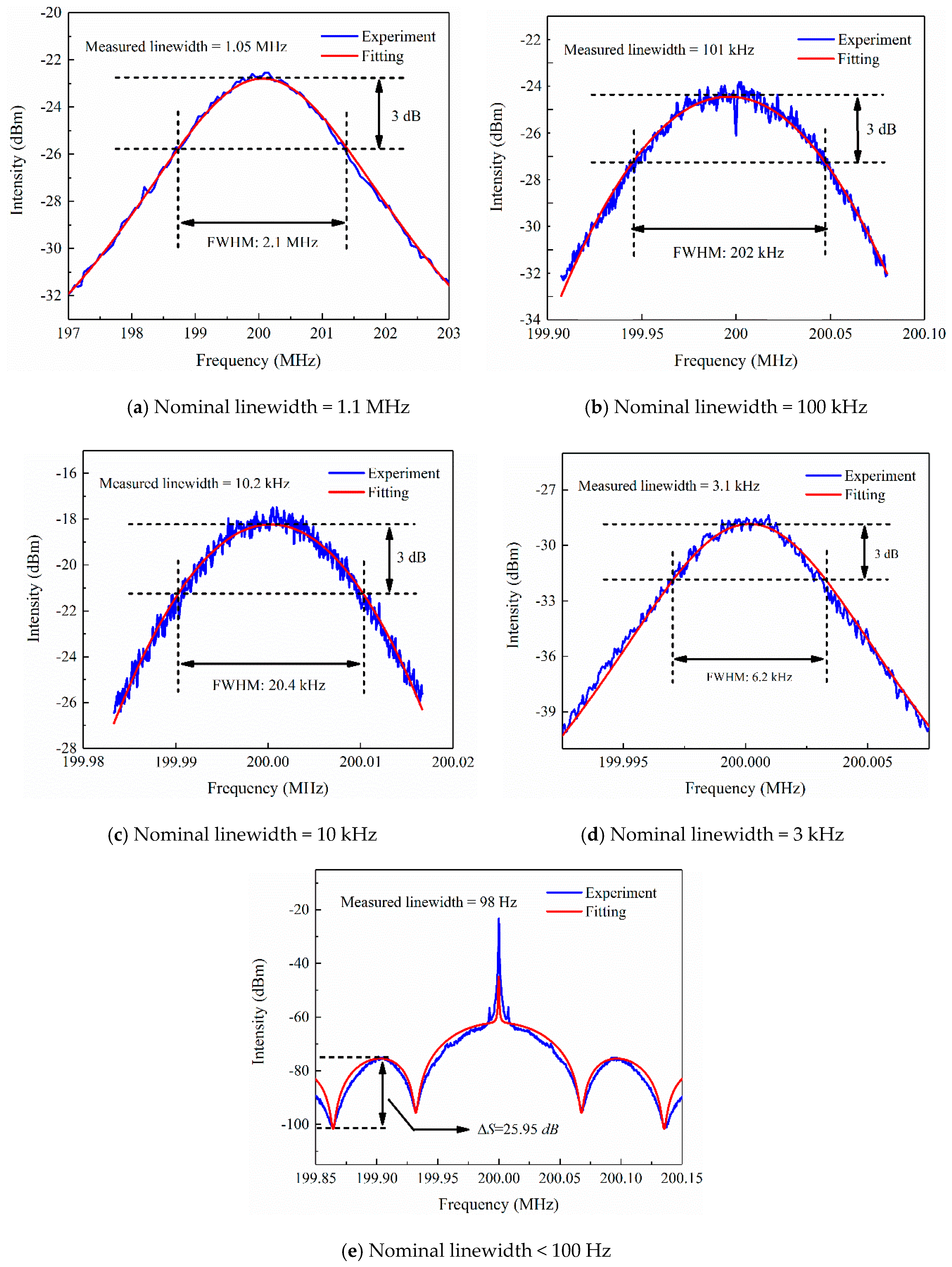



 | Model | DFB-LSM-1550-20-PM | Manufacturer |
| Wavelength | 1550.12 nm |  | |
| Nominal linewidth | 1.1 MHz | ||
| Max power | 20 mw | ||
 | Model | KG-DFB-15-M-10-S-FP | Manufacturer |
| Wavelength | 1550.12 nm |  | |
| Nominal linewidth | 100 kHz | ||
| Max power | 20 mw | ||
 | Model | COSF-SC-1550-M | Manufacturer |
| Wavelength | 1550.12 nm |  | |
| Nominal linewidth | 10 kHz | ||
| Max power | 10 mw | ||
 | Model | SDAS-NLW-PL | Manufacturer |
| Wavelength | 1550.12 nm |  | |
| Nominal linewidth | 3 kHz | ||
| Max power | 17 mw | ||
 | Model | Koheras BasiK E15 | Manufacturer |
| Wavelength | 1550.12 nm |  | |
| Nominal linewidth | <100 Hz | ||
| Max power | 40 mw |
| Laser Linewidth | Peak Power | 12 ns | 22 ns | 32 ns | 42ns | ||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | WBGS | RMSE | WBGS | RMSE | WBGS | RMSE | WBGS | ||
| ------ | dBm | MHz | MHz | MHz | MHz | MHz | MHz | MHz | MHz |
| 1.05 MHz | 23.09 | 1.090 | 108.6 | 0.524 | 93.6 | 0.399 | 92.2 | 0.360 | 89.5 |
| 101 kHz | 23.09 | 1.084 | 106.9 | 0.521 | 91.6 | 0.397 | 90.2 | 0.358 | 89.2 |
| 10.2 kHz | 23.09 | 1.021 | 105.8 | 0.460 | 90.9 | 0.335 | 90.5 | 0.272 | 89.2 |
| 3.1 kHz | 23.09 | 0.805 | 108.6 | 0.424 | 93.3 | 0.261 | 90.9 | 0.212 | 89.5 |
| 98 Hz | 23.09 | 1.051 | 107.9 | 0.531 | 92.2 | 0.409 | 88.8 | 0.306 | 89.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Q.; Yan, M.; Xue, B.; Gao, Y.; Wang, D.; Wang, Y.; Zhang, M.; Zhang, H.; Jin, B. The Influence of Laser Linewidth on the Brillouin Shift Frequency Accuracy of BOTDR. Appl. Sci. 2019, 9, 58. https://doi.org/10.3390/app9010058
Bai Q, Yan M, Xue B, Gao Y, Wang D, Wang Y, Zhang M, Zhang H, Jin B. The Influence of Laser Linewidth on the Brillouin Shift Frequency Accuracy of BOTDR. Applied Sciences. 2019; 9(1):58. https://doi.org/10.3390/app9010058
Chicago/Turabian StyleBai, Qing, Min Yan, Bo Xue, Yan Gao, Dong Wang, Yu Wang, Mingjiang Zhang, Hongjuan Zhang, and Baoquan Jin. 2019. "The Influence of Laser Linewidth on the Brillouin Shift Frequency Accuracy of BOTDR" Applied Sciences 9, no. 1: 58. https://doi.org/10.3390/app9010058
APA StyleBai, Q., Yan, M., Xue, B., Gao, Y., Wang, D., Wang, Y., Zhang, M., Zhang, H., & Jin, B. (2019). The Influence of Laser Linewidth on the Brillouin Shift Frequency Accuracy of BOTDR. Applied Sciences, 9(1), 58. https://doi.org/10.3390/app9010058