Analysis of the Hydrodynamic Effects of Gas Permeation in a Pilot-Scale Fluidized Bed Membrane Reactor
Abstract
:1. Introduction
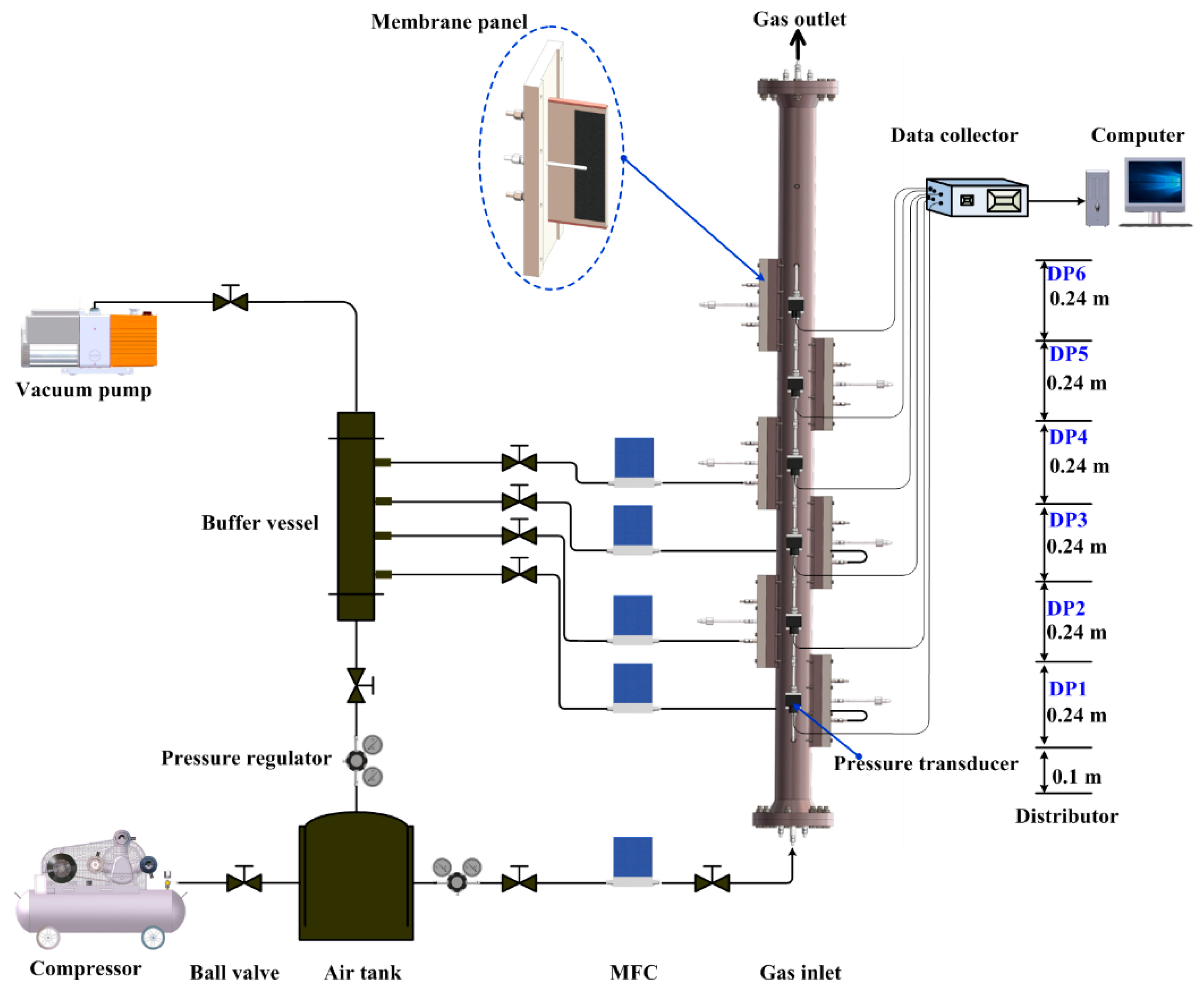
2. Experimental Setup and Procedure
3. Methods of Analysis
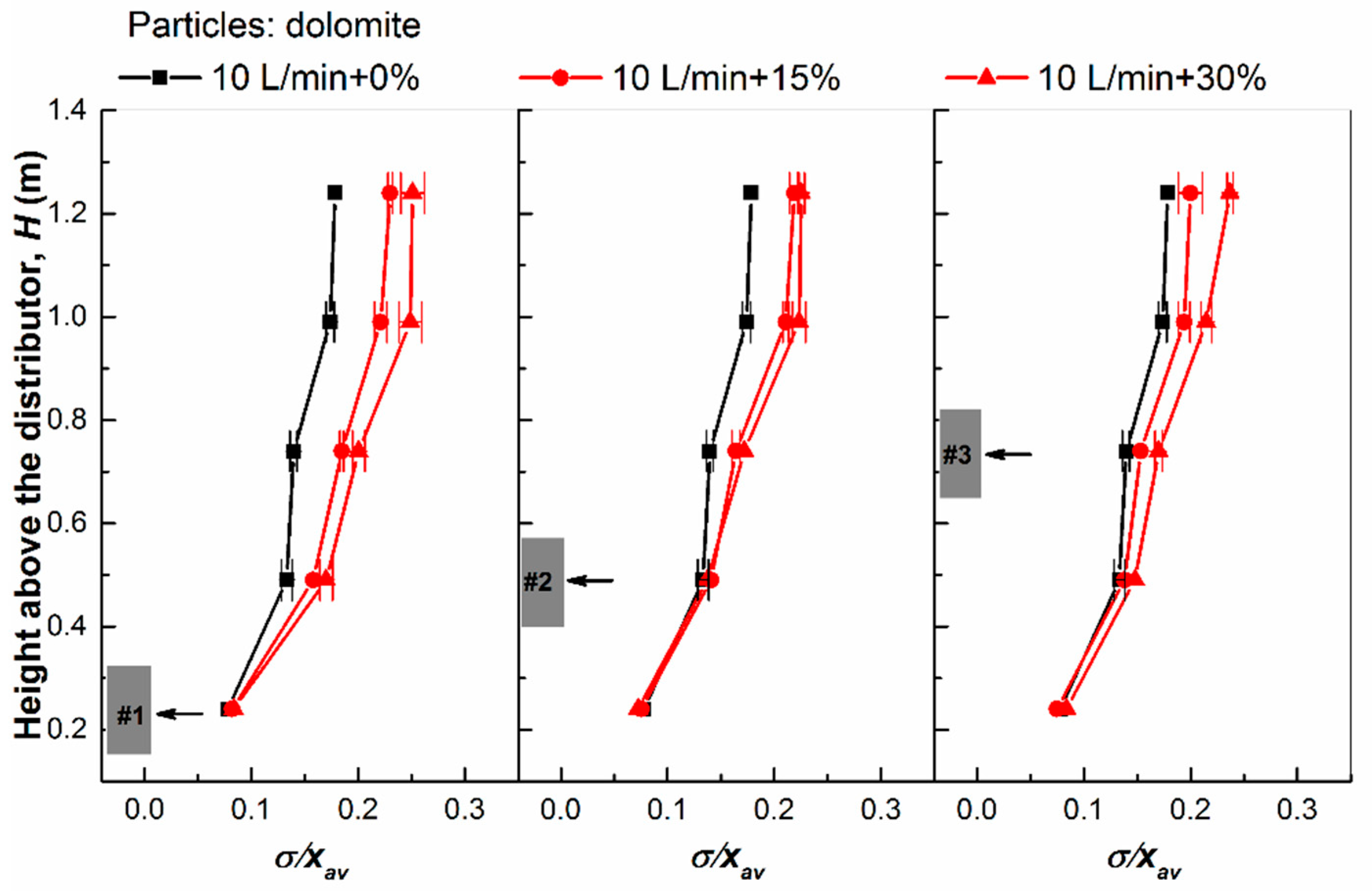
3.1. Statistical Analysis
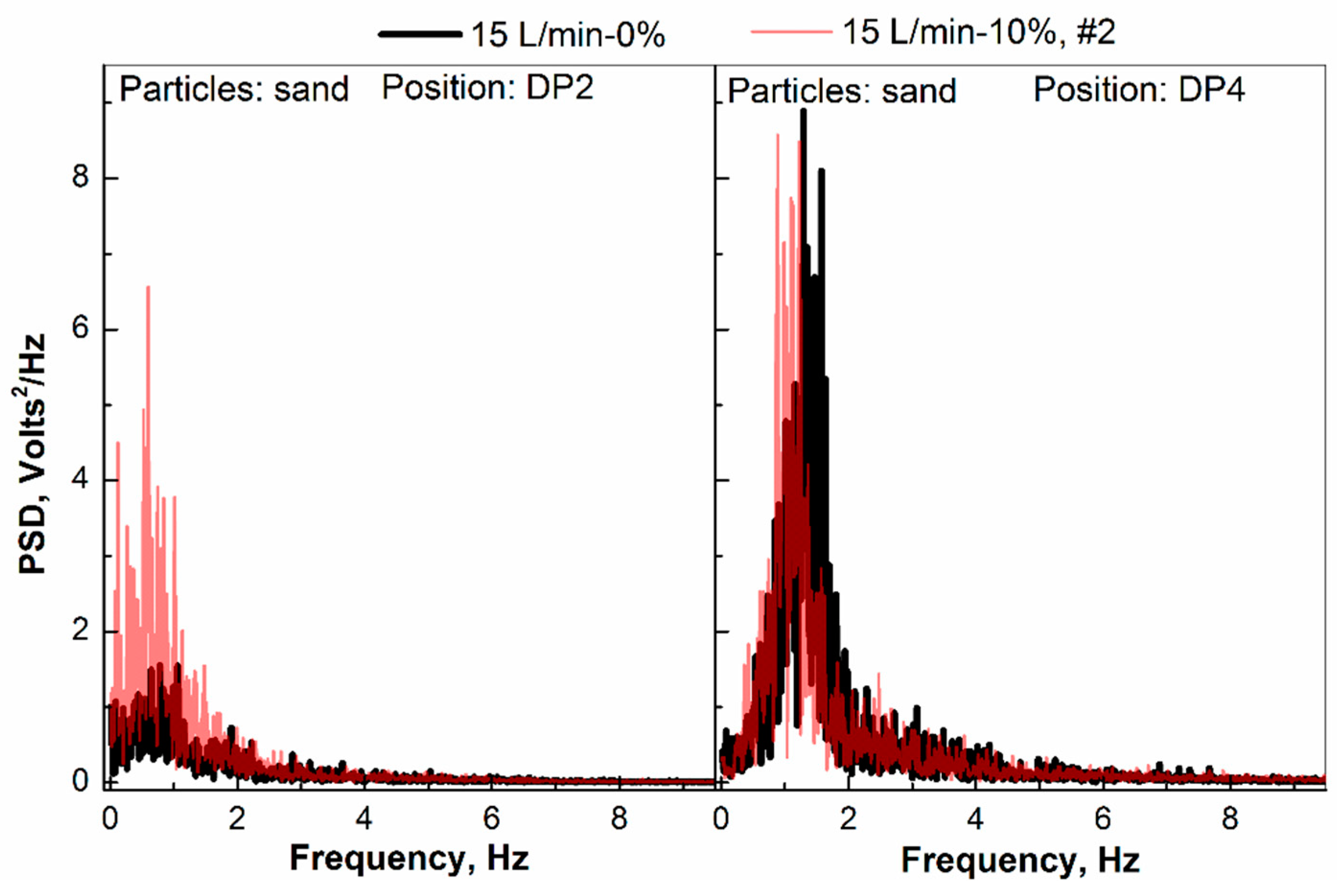
3.2. Frequency Domain Analysis
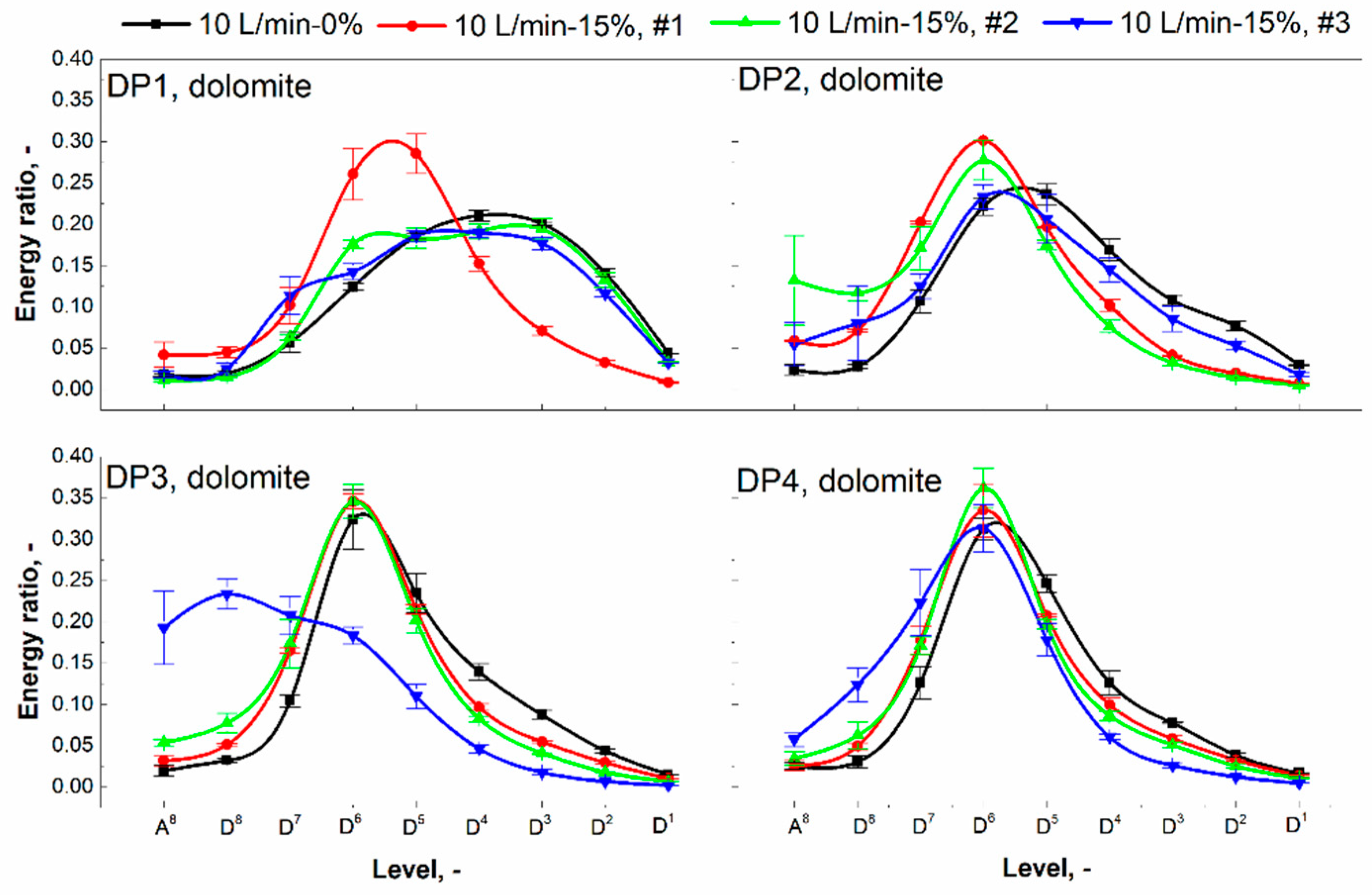
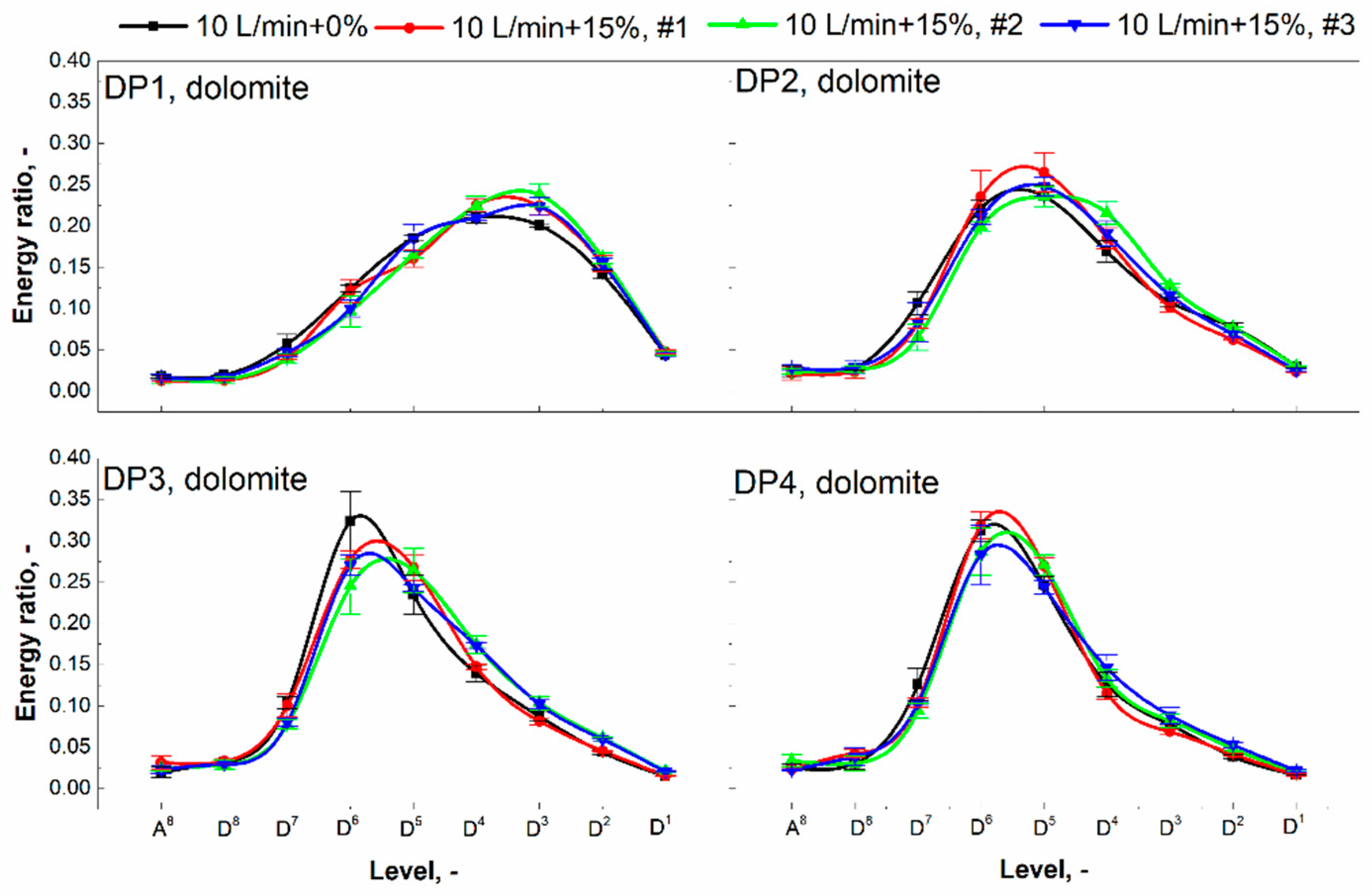
3.3. Discrete Wavelet Transform (DWT)
4. Results and Discussion
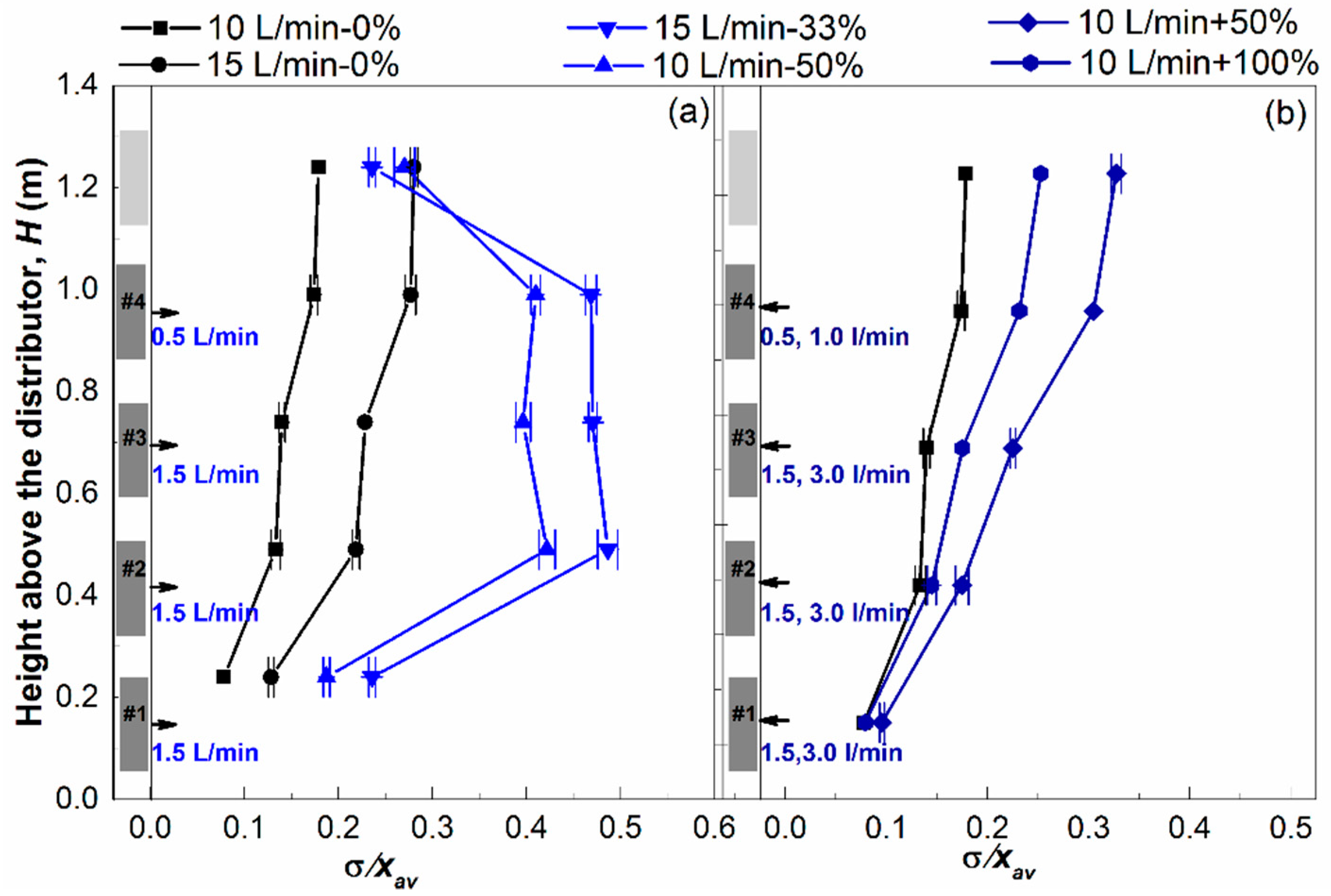
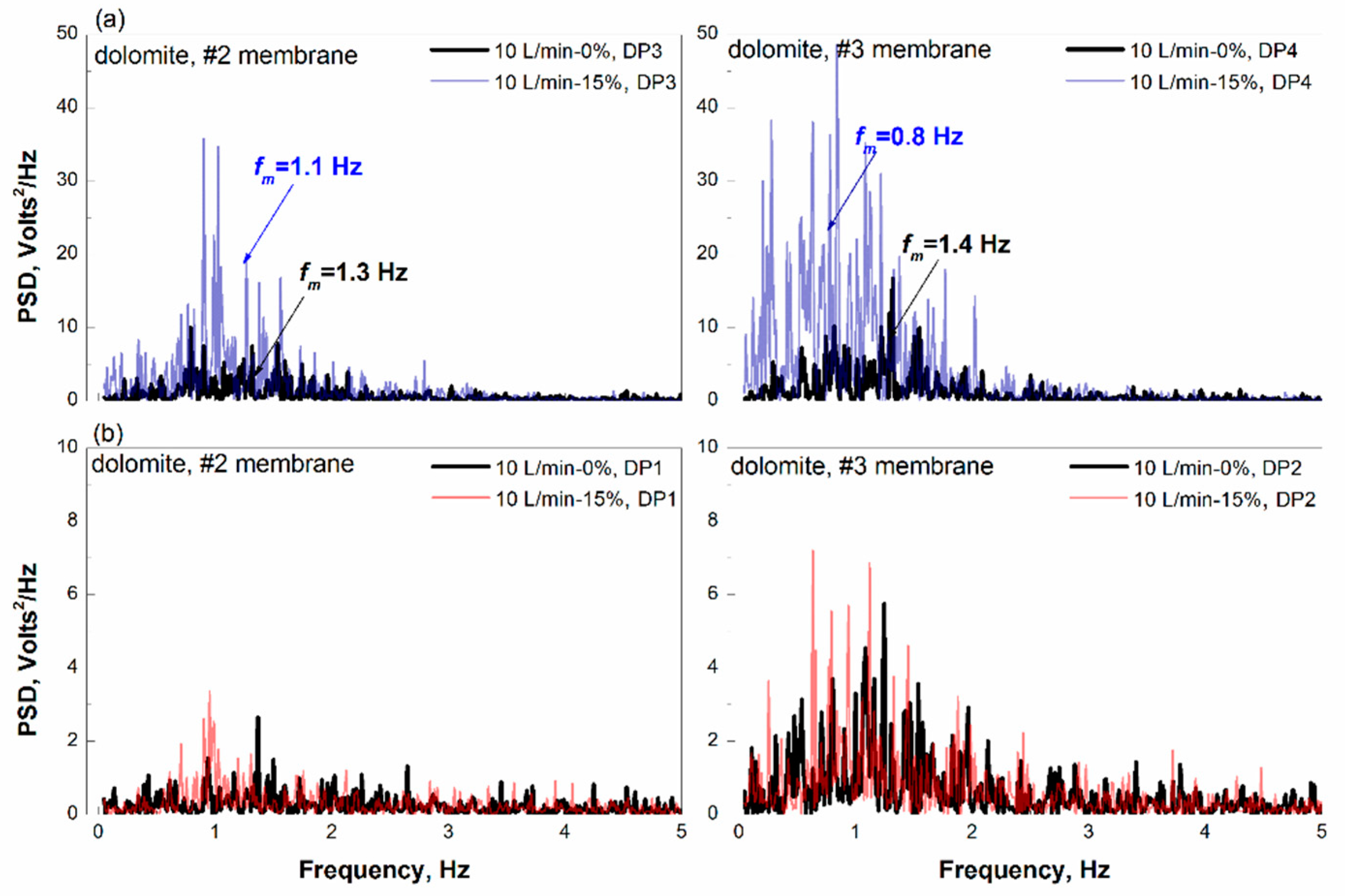
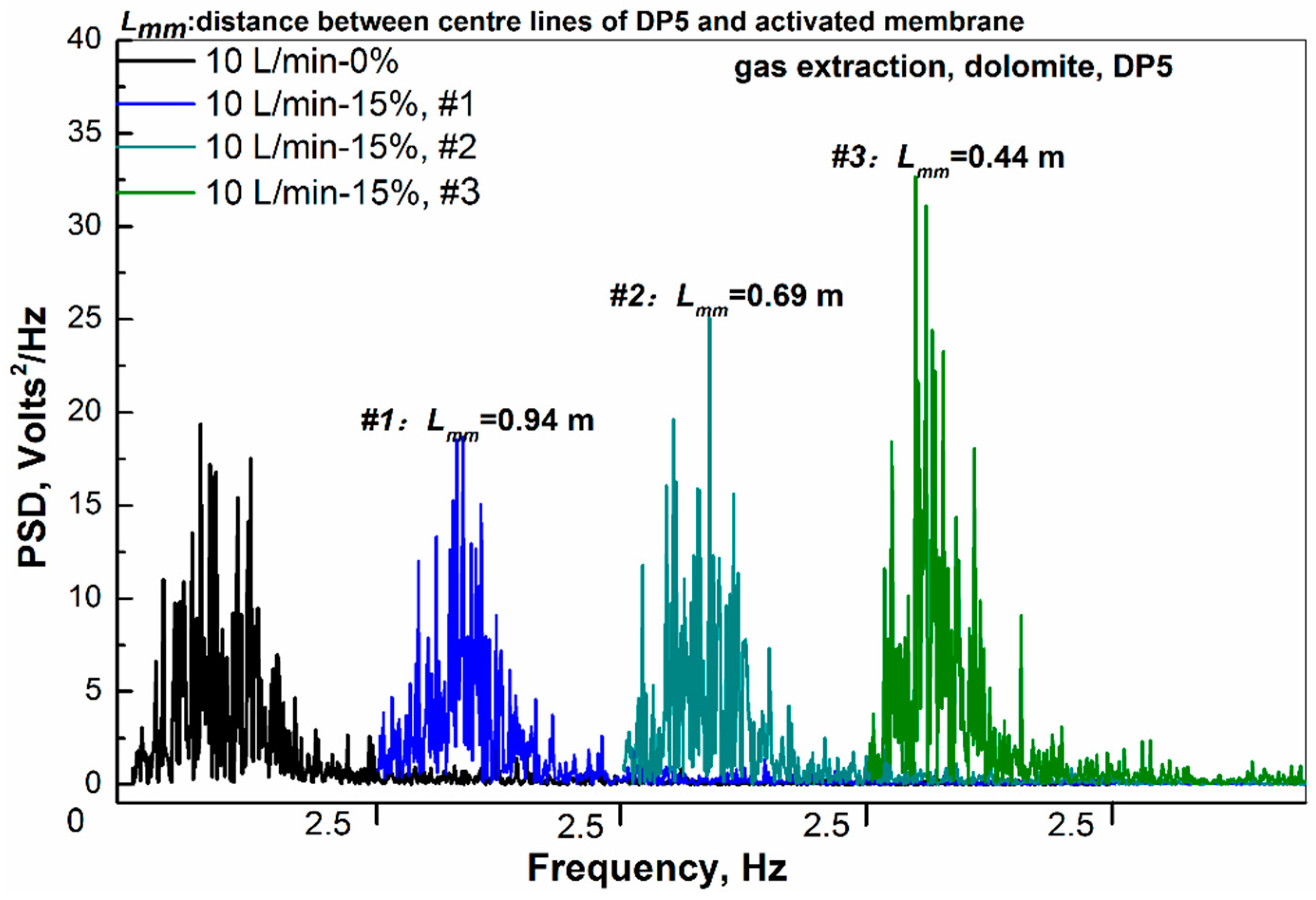
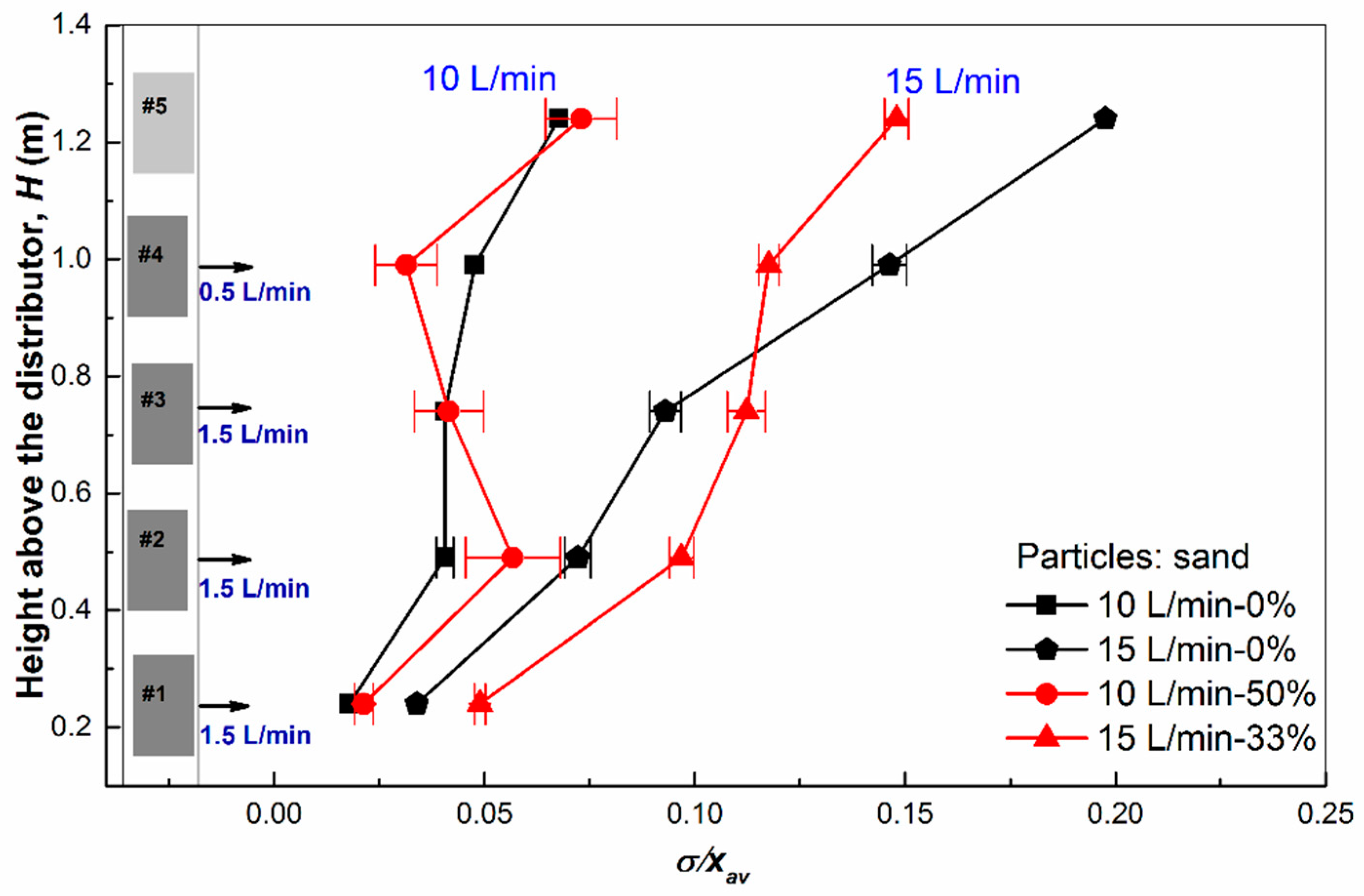
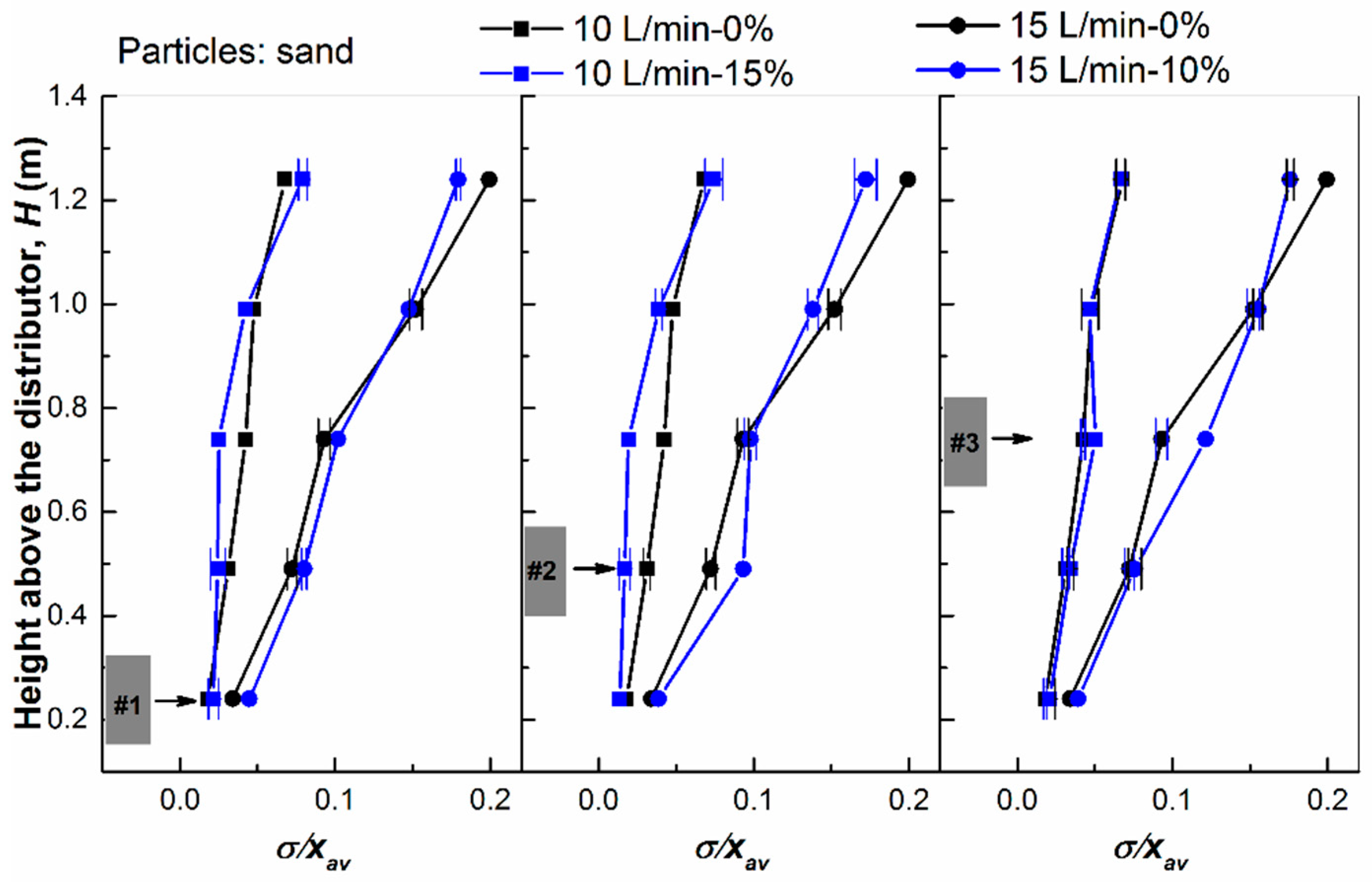
4.1. Effects of Gas Extraction
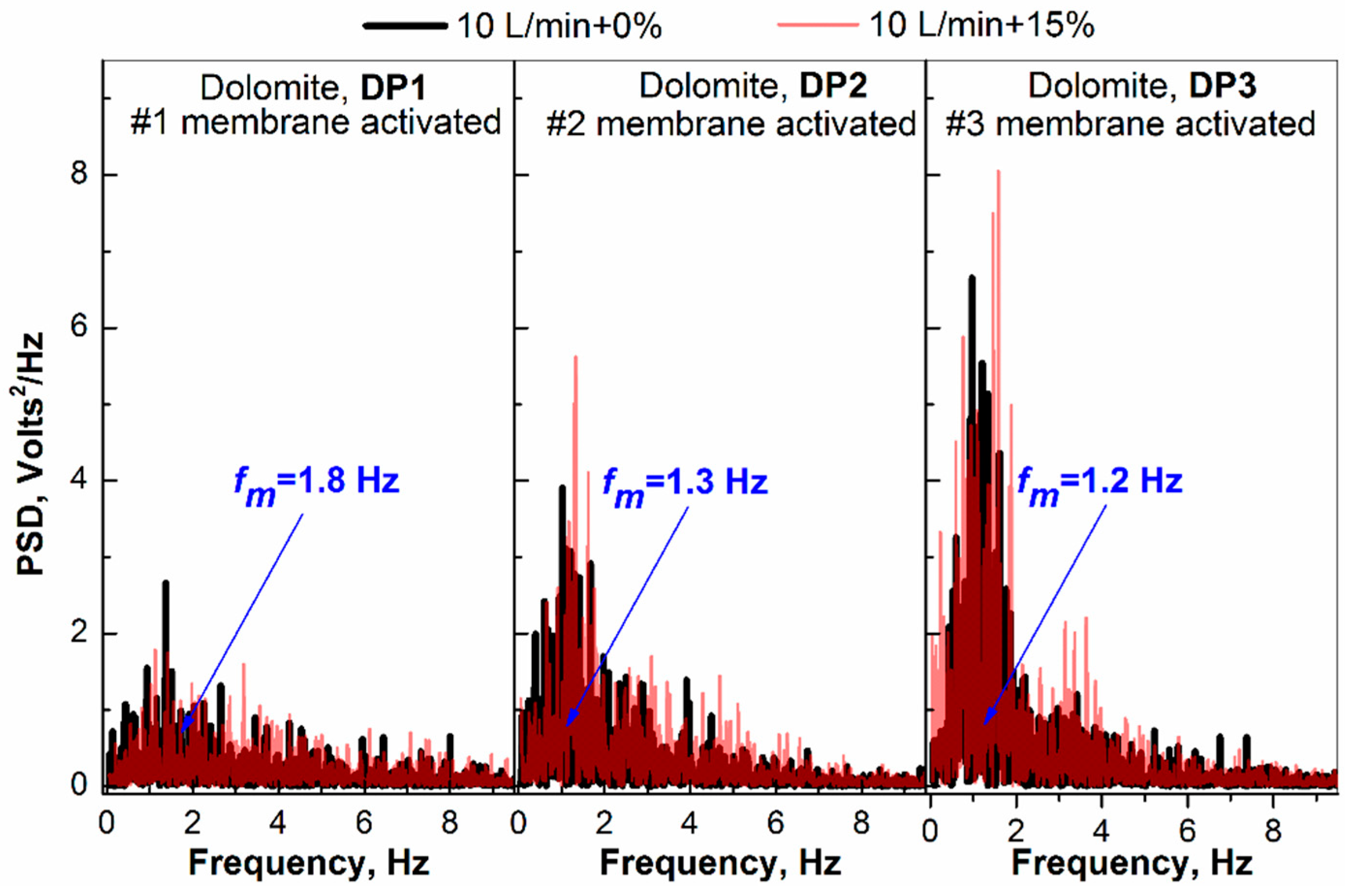
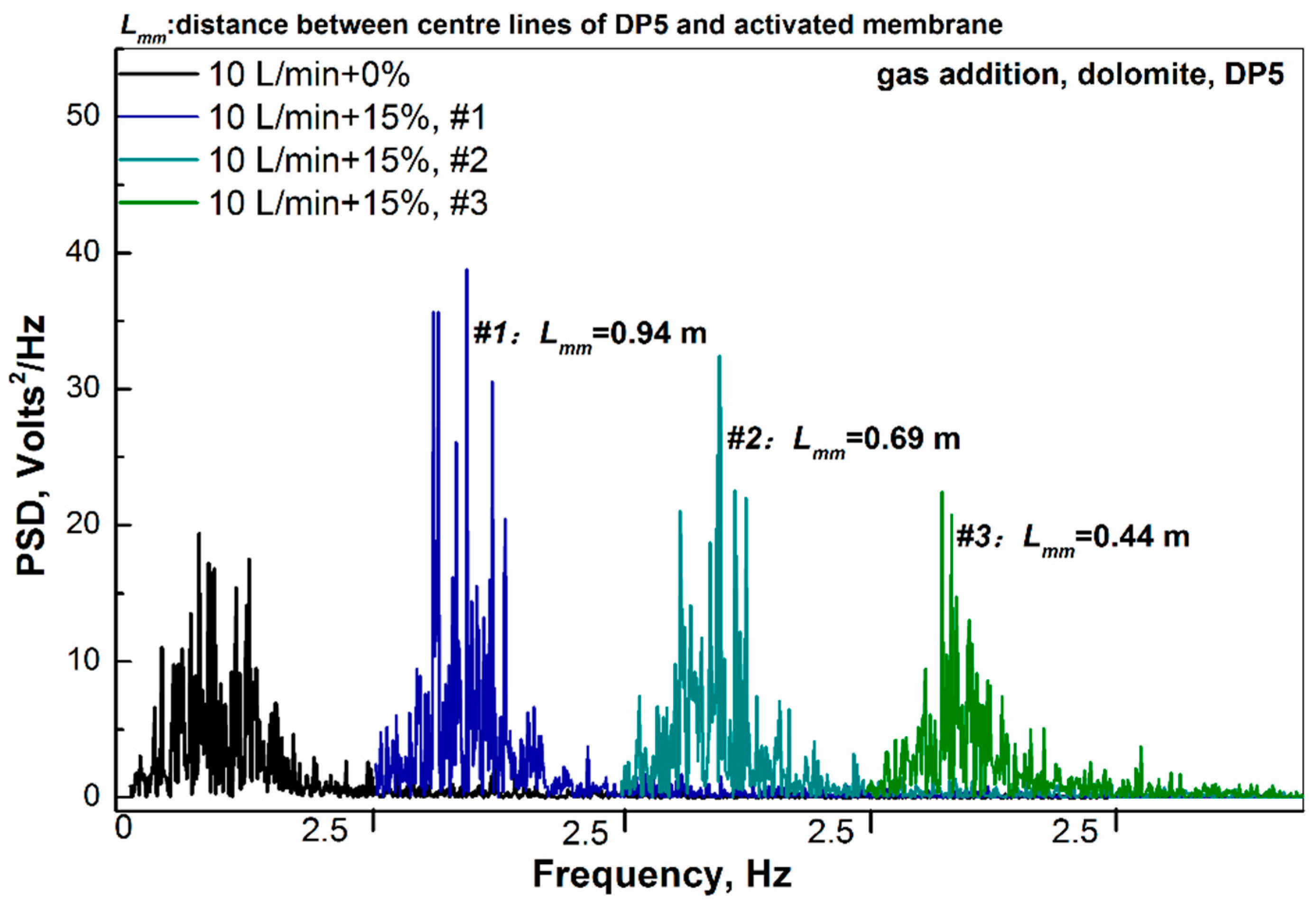
4.2. Effects of Gas Addition
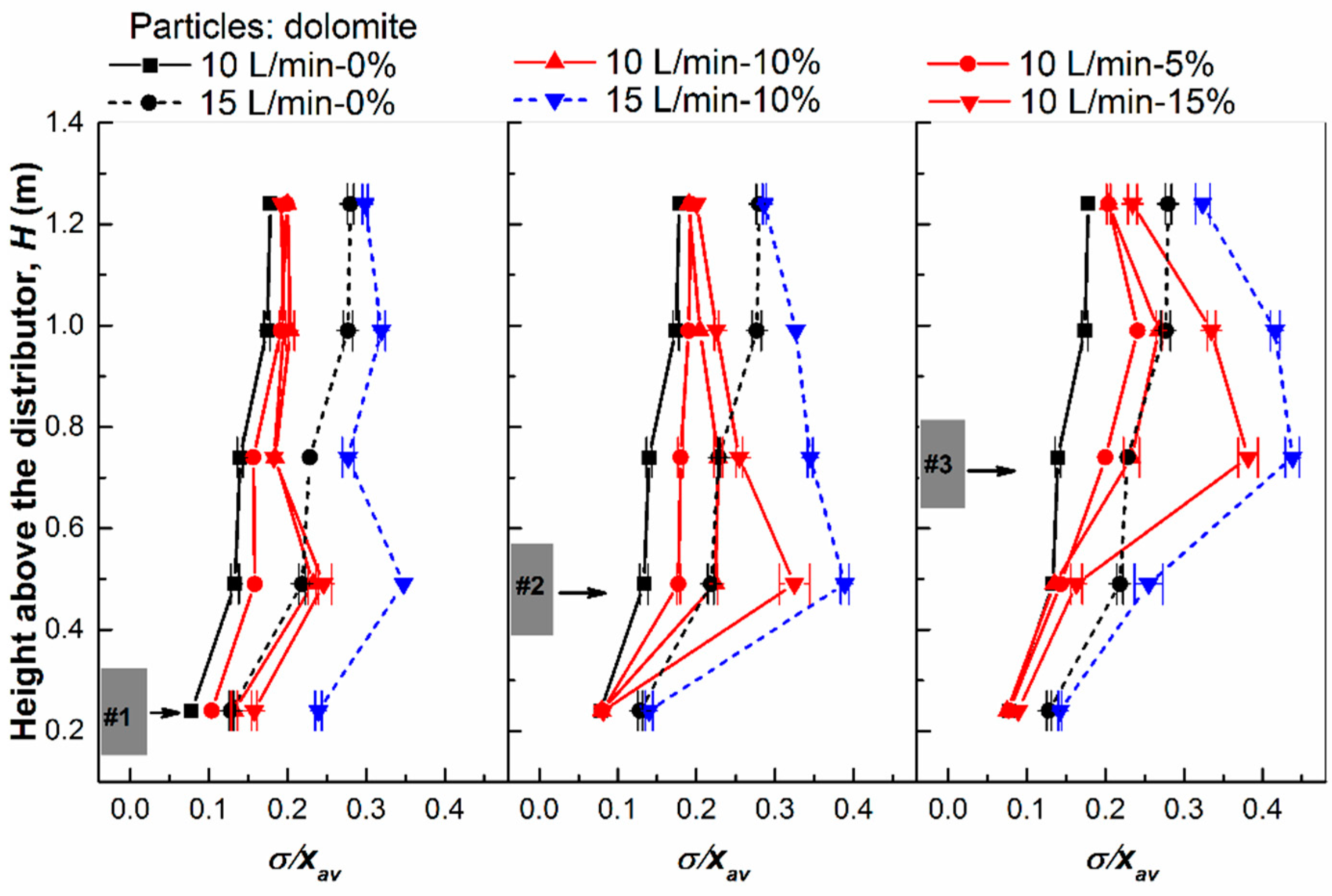
4.3. Effects of Bed Material
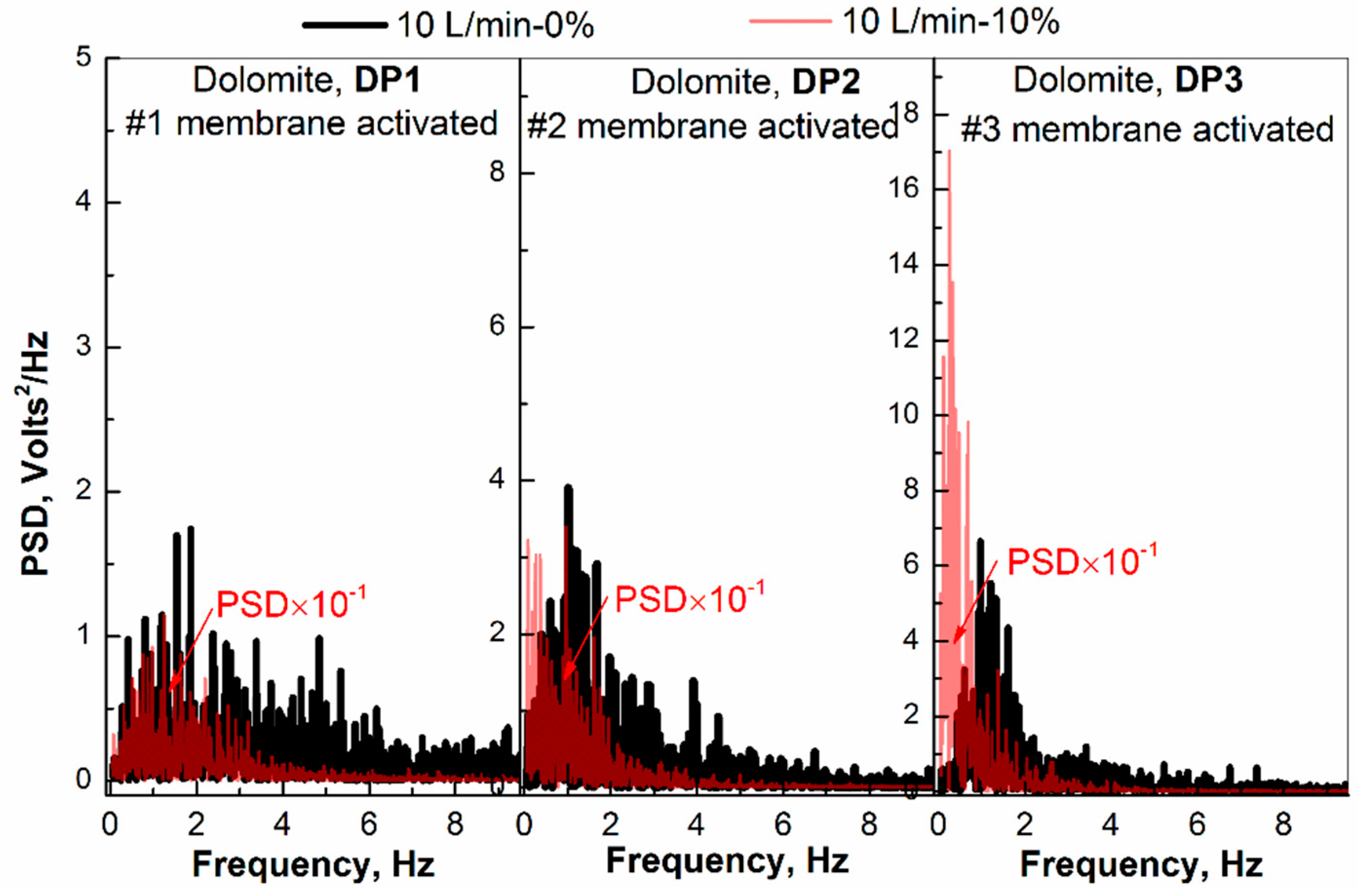
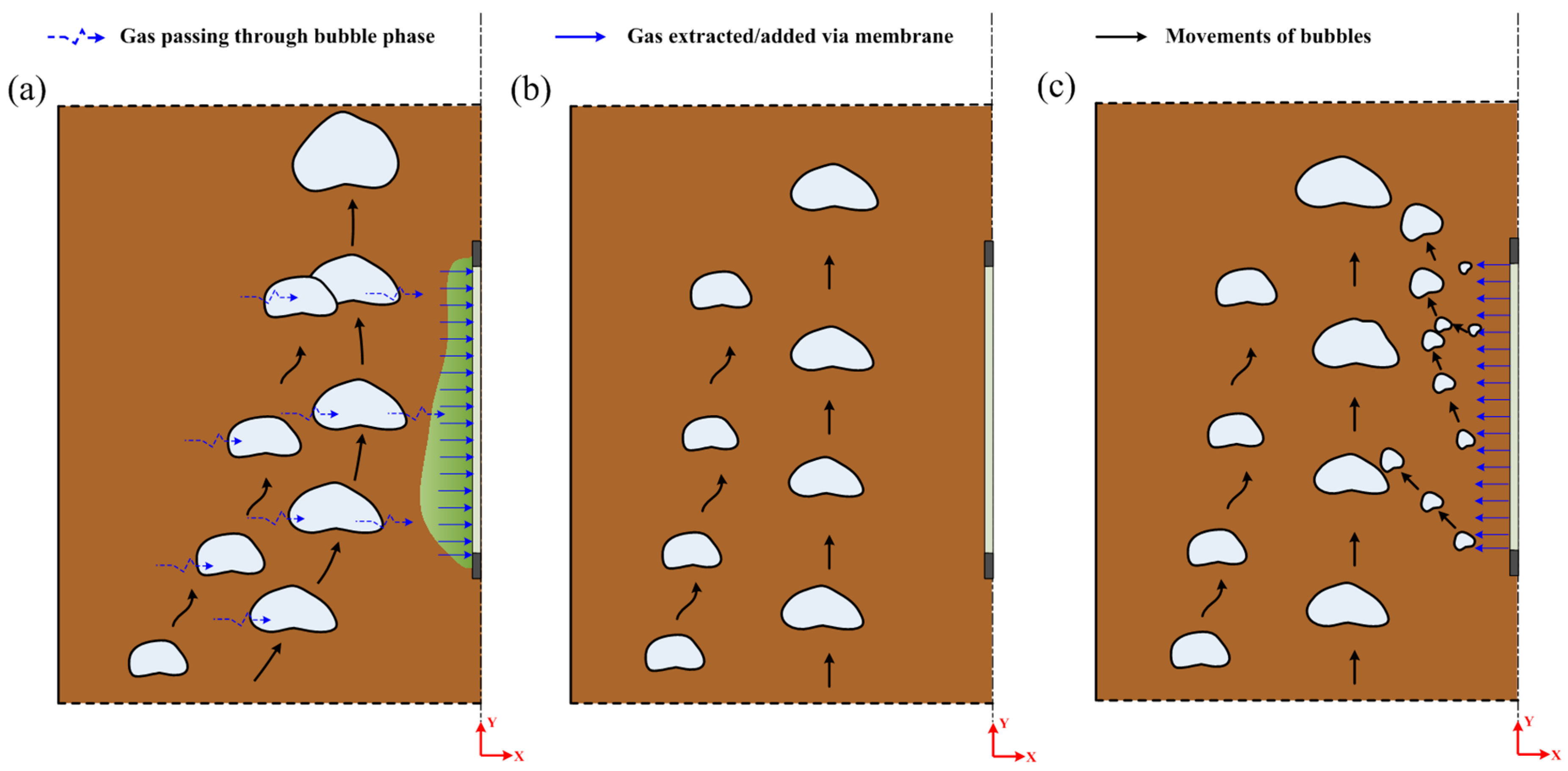
4.4. Mechanism Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Roses, L.; Gallucci, F.; Manzolini, G.; Annaland, M.V. Experimental study of steam methane reforming in a Pd-based fluidized bed membrane reactor. Chem. Eng. J. 2013, 222, 307–320. [Google Scholar] [CrossRef]
- Fernandez, E.; Helmi, A.; Coenen, K.; Melendez, J.; Viviente, J.L.; Tanaka, D.A.P.; Annaland, M.V.; Gallucci, F. Development of thin Pd-Ag supported membranes for fluidized bed membrane reactors including WGS related gases. Int. J. Hydrog. Energy 2015, 40, 3506–3519. [Google Scholar] [CrossRef]
- Andrés, M.; Boyd, T.; Gulamhusein, A.; Comyn, N.; Lim, C.J.; Grace, J.R.; Shirasaki, Y.; Isamu, Y. Pure Hydrogen generation in a fluidized-bed membrane reactor: Experimental findings. Chem. Eng. Sci. 2008, 63, 2752–2762. [Google Scholar] [CrossRef]
- Patil, C.S.; Annaland, M.V.; Kuipers, J.A.M. Fluidised bed membrane reactor for ultrapure hydrogen production via methane steam reforming: Experimental demonstration and model validation. Chem. Eng. Sci. 2007, 62, 2989–3007. [Google Scholar] [CrossRef]
- Chen, Z.; Grace, J.R.; Lim, C.J.; Li, A. Experimental studies of pure hydrogen production in a commercialized fluidized-bed membrane reactor with SMR and ATR catalysts. Int. J. Hydrog. Energy 2007, 32, 2359–2366. [Google Scholar] [CrossRef]
- Arratibel, A.; Tanaka, A.P.; Laso, I.; Annaland, M.V.; Gallucci, F. Development of Pd-based double-skinned membranes for hydrogen production in fluidized bed membrane reactors. J. Membr. Sci. 2018, 550, 536–544. [Google Scholar] [CrossRef]
- Rakib, M.A.; Grace, J.R.; Lim, C.J.; Elnashaie, S.S.E.H. Steam reforming of heptane in a fluidized bed membrane reactor. J. Power Sources 2010, 195, 5749–5760. [Google Scholar] [CrossRef]
- Gimeno, M.P.; Wu, Z.T.; Soler, J.; Herguido, J.; Li, K.; Menédez, M. Combination of a two-zone fluidized bed reactor with a Pd hollow fibre membrane for catalytic alkane dehydrogenation. Chem. Eng. J. 2009, 155, 298–303. [Google Scholar] [CrossRef]
- Al-Sherehy, F.; Grace, J.R.; Adris, A.E.M. The influence of distributed reactant injection along the height of a fluidized bed reactor. Chem. Eng. Sci. 2005, 60, 7121–7130. [Google Scholar] [CrossRef]
- Jao, S.; Arellanoi-Garcia, H.; Wozny, G. Oxidative coupling of methane in a fluidized bed reactor: Influence of feeding policy, hydrodynamics, and reactor geometry. Chem. Eng. J. 2011, 171, 255–271. [Google Scholar] [CrossRef] [Green Version]
- Deshmukh, S.A.R.K.; Laverman, J.A.; Annaland, M.V.; Kuipers, J.A.M. Development of a membrane-assisted fluidized bed reactor. 2. Experimental demonstration and modeling for the partial oxidation of methanol. Ind. Eng. Chem. Res. 2005, 44, 5966–5976. [Google Scholar] [CrossRef]
- Christensen, D.; Nijenhuis, J.; van Ommen, J.R.; Coppens, M.O. Influence of distributed secondary gas injection on the performance of a bubbling fluidized-bed reactor. Ind. Eng. Chem. Res. 2008, 47, 3601–3618. [Google Scholar] [CrossRef]
- Christensen, D.; Vervloet, D.; Nijenhuis, J.; van Wachem, B.G.M.; van Ommen, J.R.; Coppens, M.O. Insights in distributed secondary gas injection in a bubbling fluidized bed via discrete particle simulations. Powder Technol. 2008, 183, 454–466. [Google Scholar] [CrossRef]
- Christensen, D.J.; Nijenhuis, J.; van Ommen, J.R.; Coppens, M.O. Residence times in fluidized beds with secondary gas injection. Powder Technol. 2008, 180, 321–331. [Google Scholar] [CrossRef]
- Mleczko, L.; Ostrowski, T.; Wurzel, T. A fluidized-bed membrane reactor for the catalytic partial oxidation of methane to synthesis gas. Chem. Eng. Sci. 1996, 51, 3187–3192. [Google Scholar] [CrossRef]
- De Jong, J.F.; Annaland, M.V.; Kuipers, J.A.M. Experimental study on the effects of gas permeation through flat membranes on the hydrodynamics in membrane-assisted fluidized beds. Chem. Eng. Sci. 2011, 66, 2398–2408. [Google Scholar] [CrossRef]
- Dang, N.T.Y.; Gallucci, F.; Annaland, M.V. Micro-structured fluidized bed membrane reactor: Solids circulation and densified zones distribution. Chem. Eng. J. 2014, 239, 42–52. [Google Scholar] [CrossRef]
- Wassie, S.A.; Cloete, S.; Zaabout, A.; Gallucci, F.; Annaland, M.V.; Amini, S. Experimental investigation on the generic effects of gas permeation through flat vertical membranes. Powder Technol. 2017, 316, 207–217. [Google Scholar] [CrossRef]
- Wassie, S.A.; Zaabout, A.; Gallucci, F.; Cloete, S.; Annaland, M.V.; Amini, S. Detecting densified zone formation in membrane-assisted fluidized bed reactors through pressure measurements. Chem. Eng. J. 2017, 308, 1154–1164. [Google Scholar] [CrossRef]
- Helmi, A.; Wagner, E.C.; Gallucci, F.; Annaland, M.V.; van Ommen, J.R.; Mudde, R.F. On the hydrodynamics of membrane assisted fluidized bed reactors using X-ray analysis. Chem. Eng. Process. 2017, 122, 508–522. [Google Scholar] [CrossRef] [Green Version]
- De Jong, J.F.; Annaland, M.V.; Kuipers, J.A.M. Experimental study on the hydrodynamic effects gas permeation through horizontal membrane tubes in fluidized beds. Powder Technol. 2013, 241, 74–84. [Google Scholar] [CrossRef]
- Julián, I.; Herguido, J.; Menéndez, M. Gas permeation effect on the two-section two-zone fluidized bed membrane reactor (TS-TZFBMR) fluid dynamics: A CFD simulation study. Chem. Eng. J. 2016, 305, 201–211. [Google Scholar] [CrossRef]
- Dang, T.Y.N.; Gallucci, F.; Annaland, M.V. Gas back-mixing study in a membrane-assisted micro-structured fluidized bed. Chem. Eng. Sci. 2014, 108, 194–202. [Google Scholar] [CrossRef]
- Min, J.; Drake, J.B.; Heindel, T.; Fox, R. Experimental validation of CFD simulation of a Lab-scale fluidized-bed reactor with and without side-gas injection. AIChE J. 2010, 56, 1434–1445. [Google Scholar] [CrossRef]
- Wassie, S.A.; Gallucci, F.; Cloete, S.; Zaabout, A.; Annaland, M.V.; Amini, S. The effect of gas permeation through vertical membrane on chemical switching reforming (CSR) reactor performance. Int. J. Hydrog. Energy 2016, 41, 8640–8655. [Google Scholar] [CrossRef]
- Gómez-Hernández, J.; Sánchez-Prieto, J.; Briongos, J.V.; Santana, D. Wide band energy analysis of fluidized bed pressure fluctuation signals using a frequency division method. Chem. Eng. Sci. 2014, 105, 92–103. [Google Scholar] [CrossRef] [Green Version]
- Bi, H.T.; Grace, J.R.; Zhu, J. Propagation of pressure waves and forced oscillations in gas-solid fluidized beds and their influence on diagnostics of local hydrodynamics. Powder Technol. 1995, 82, 239–253. [Google Scholar] [CrossRef]
- Van der Schaaf, J.; Schouten, J.C.; van den Bleek, C.M. Origin, propagation and attenuation of pressure waves in gas-solid fluidized beds. Powder Technol. 1998, 95, 220–233. [Google Scholar] [CrossRef]
- Chen, Y.; Lim, C.J.; Grace, J.R.; Zhang, J.; Zhao, Y. Characterization of pressure fluctuations from a gas-solid fluidized bed by structure density function analysis. Chem. Eng. Sci. 2015, 129, 156–167. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, W.; Grace, J.R.; Zhao, Y.; Zhang, J.; Li, Y. Direct resolution of differential pressure fluctuations to characterize multi-scale dynamics in a gas fluidized bed. Int. J. Multiph. Flow 2016, 85, 380–394. [Google Scholar] [CrossRef]
- Rakib, M.A.; Grace, J.R.; Lim, C.J.; Elnashaie, S.S.E.H. Steam reforming of propane in a fluidized bed membrane reactor for hydrogen production. Int. J. Hydrog. Energy 2010, 35, 6276–6299. [Google Scholar] [CrossRef]
- Peters, T.A.; Stange, M.; Bredense, R. On the high pressure performance of thin supported Pd-23%Ag membrane-evidence of ultrahigh hydrogen flux after air treatment. J. Membr. Sci. 2011, 378, 28–34. [Google Scholar] [CrossRef]
- Johnsson, F.; Zijerveld, R.C.; Schouten, J.C.; van den Bleek, C.M.; Lecker, B. Characterization of fluidization regimes by time-series analysis of pressure fluctuations. Int. J. Multiph. Flow 2000, 26, 663–715. [Google Scholar] [CrossRef]
- Zhao, G.B.; Yang, Y.R. Multiscale resolution of fluidized-bed pressure fluctuations. AIChE J. 2003, 49, 869–882. [Google Scholar] [CrossRef]
- Wu, B.; Kantzas, A.; Bellehuneur, C.T.; He, Z.; Kryuchkov, S. Multiresolution analysis of pressure fluctuations in a gas-solids fluidized bed: Application to glass beads and polyethylene powder systems. Chem. Eng. J. 2007, 131, 23–33. [Google Scholar] [CrossRef]
- Darton, R.C.; Lanauuze, R.D.; Davidson, J.F.; Harrison, D. Bubble growth due to coalescence in fluidized-beds. Trans. Inst. Chem. Eng. 1977, 55, 274–280. [Google Scholar]
- Zaabout, A.; Bernus, A.; Cloete, S.; Amini, S. The effect of gas addition on bubble dynamics in a fluidized bed with flat vertical membranes. Chem. Eng. J. 2018, 344, 71–85. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]

| Material | Diameter Range (mm) | Particle Density, ρp (kg/m3) | Umf (m/s) |
|---|---|---|---|
| Calcined dolomite | 0.18–0.212 | 1450 | 0.041 |
| Silica sand | 0.18–0.212 | 2520 | 0.069 |
| Campaign | Membranes Activated | Bed Material | Permeation Rate (L/min) | U (m/s) |
|---|---|---|---|---|
| Ref. 1 | 0 | Calcined dolomite | 0 | 0.004–0.37 |
| Ref. 2 | 0 | Silica sand | 0 | 0.004–0.37 |
| #1-0 | Membrane #1-4 | Calcined dolomite | 5, 10 | 0.09–0.14 |
| #1-1 | Membrane #1 | Calcined dolomite | 1.5, 3.0 | 0.09–0.14 |
| #1-2 | Membrane #2 | Calcined dolomite | 1.5, 3.0 | 0.09–0.14 |
| #1-3 | Membrane #3 | Calcined dolomite | 1.5, 3.0 | 0.09–0.14 |
| #1-4 | Membrane #1-4 | Silica sand | 5, 10 | 0.09–0.14 |
| #1-5 | Membrane #1 | Silica sand | 1.5, 3.0 | 0.09–0.14 |
| #1-6 | Membrane #2 | Silica sand | 1.5, 3.0 | 0.09–0.14 |
| #1-7 | Membrane #3 | Silica sand | 1.5–3.0 | 0.09–0.14 |
| #2-0 | Membrane #1-4 | Calcined dolomite | −5 | 0.09–0.14 |
| #2-1 | Membrane #1 | Calcined dolomite | −0.5, −1.0, −1.5 | 0.09–0.14 |
| #2-2 | Membrane #2 | Calcined dolomite | −0.5, −1.0, −1.5 | 0.09–0.14 |
| #2-3 | Membrane #3 | Calcined dolomite | −0.5, −1.0, −1.5 | 0.09–0.14 |
| #2-4 | Membrane #1-4 | Silica sand | −5 | 0.09–0.14 |
| #2-5 | Membrane #1 | Silica sand | −1.0, −1.5 | 0.09–0.14 |
| #2-6 | Membrane #2 | Silica sand | −1.0, −1.5 | 0.09–0.14 |
| #2-7 | Membrane #3 | Silica sand | −1.0, −1.5 | 0.09–0.14 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, C.; Xiao, Y.; Peng, R.; Grace, J.R.; Chen, Y. Analysis of the Hydrodynamic Effects of Gas Permeation in a Pilot-Scale Fluidized Bed Membrane Reactor. Appl. Sci. 2019, 9, 67. https://doi.org/10.3390/app9010067
Bai C, Xiao Y, Peng R, Grace JR, Chen Y. Analysis of the Hydrodynamic Effects of Gas Permeation in a Pilot-Scale Fluidized Bed Membrane Reactor. Applied Sciences. 2019; 9(1):67. https://doi.org/10.3390/app9010067
Chicago/Turabian StyleBai, Chenxi, Yao Xiao, Ruifeng Peng, John R. Grace, and Yumin Chen. 2019. "Analysis of the Hydrodynamic Effects of Gas Permeation in a Pilot-Scale Fluidized Bed Membrane Reactor" Applied Sciences 9, no. 1: 67. https://doi.org/10.3390/app9010067
APA StyleBai, C., Xiao, Y., Peng, R., Grace, J. R., & Chen, Y. (2019). Analysis of the Hydrodynamic Effects of Gas Permeation in a Pilot-Scale Fluidized Bed Membrane Reactor. Applied Sciences, 9(1), 67. https://doi.org/10.3390/app9010067





