Accurate Computation of Airfoil Flow Based on the Lattice Boltzmann Method
Abstract
:1. Introduction
2. The Lattice Boltzmann Method
3. Computation Model
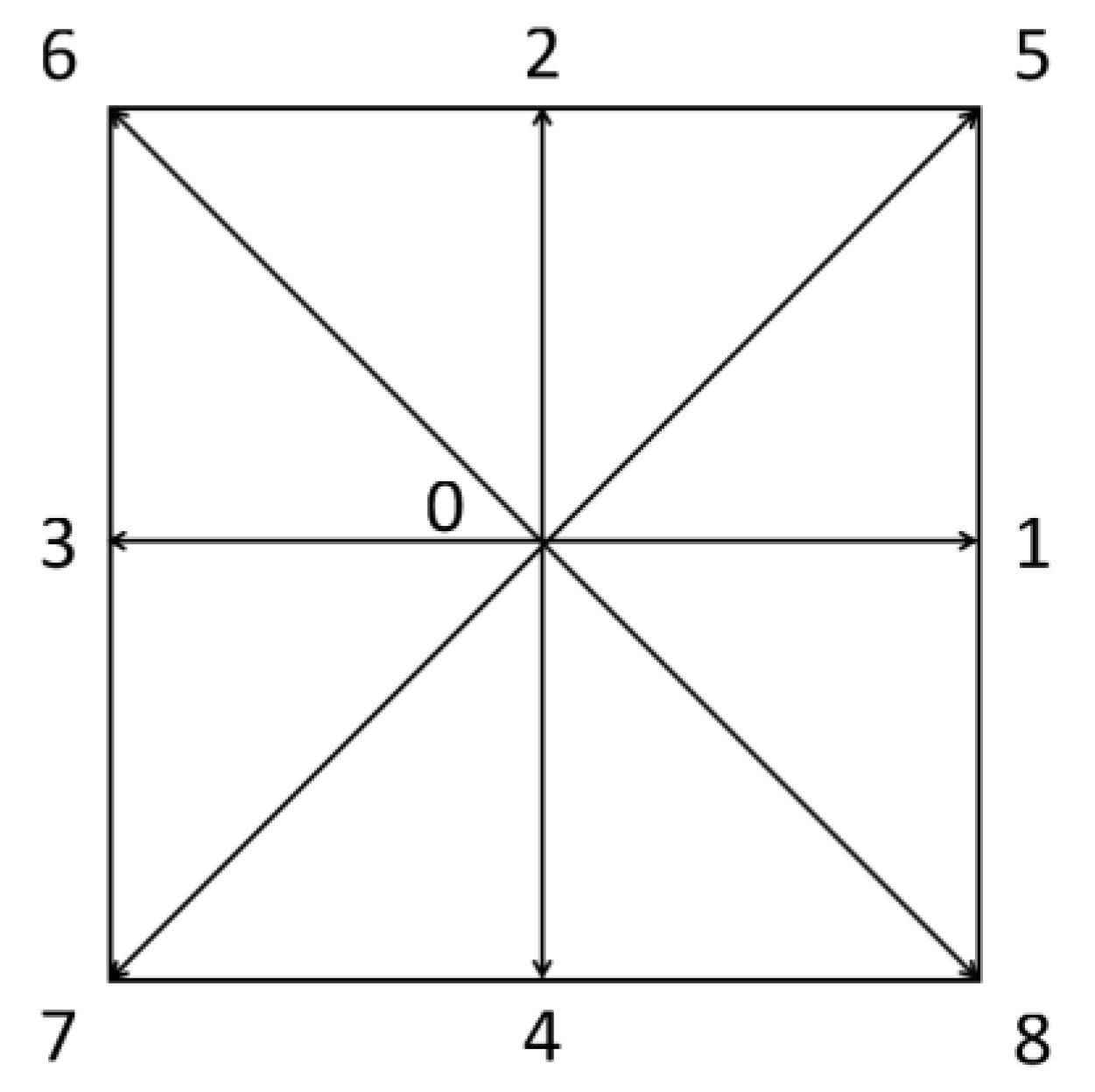
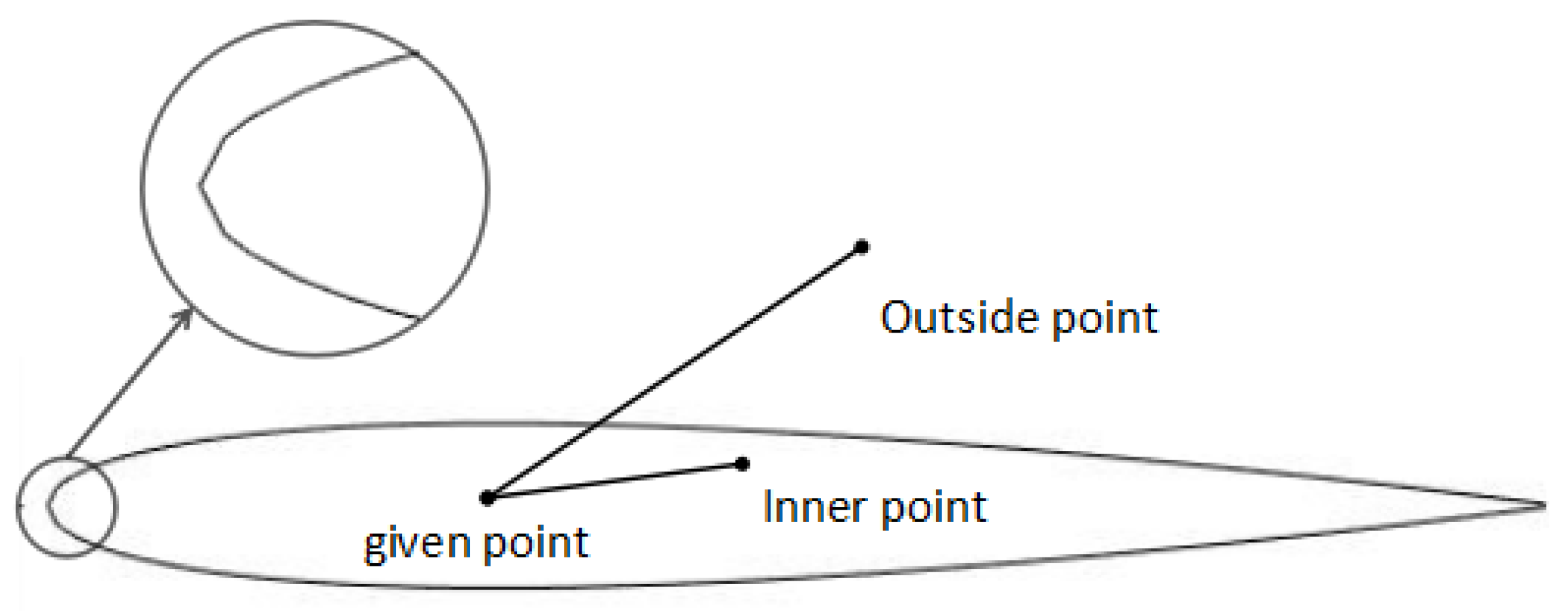
3.1. Generation of Airfoil, Judgment of Grid Point Type
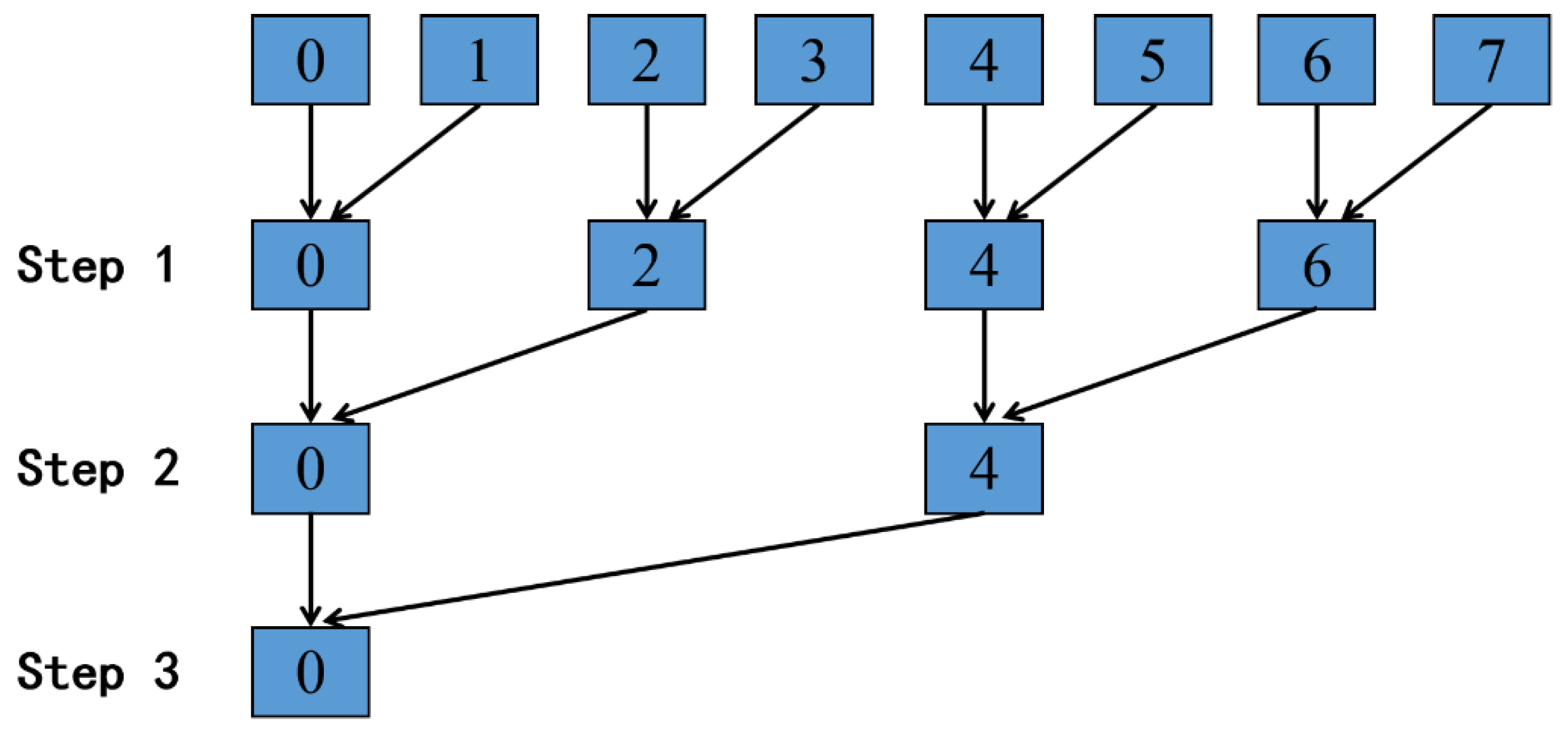
3.2. Data Partition and Communication
3.3. Many-Core Structure and Communication of the Sunway TaihuLight
4. Experiment and Results
4.1. Experimental Environment
4.2. Numerical Experimental Results
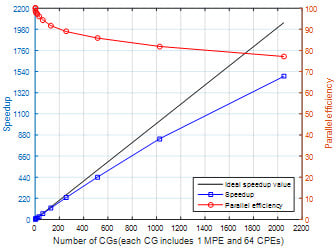
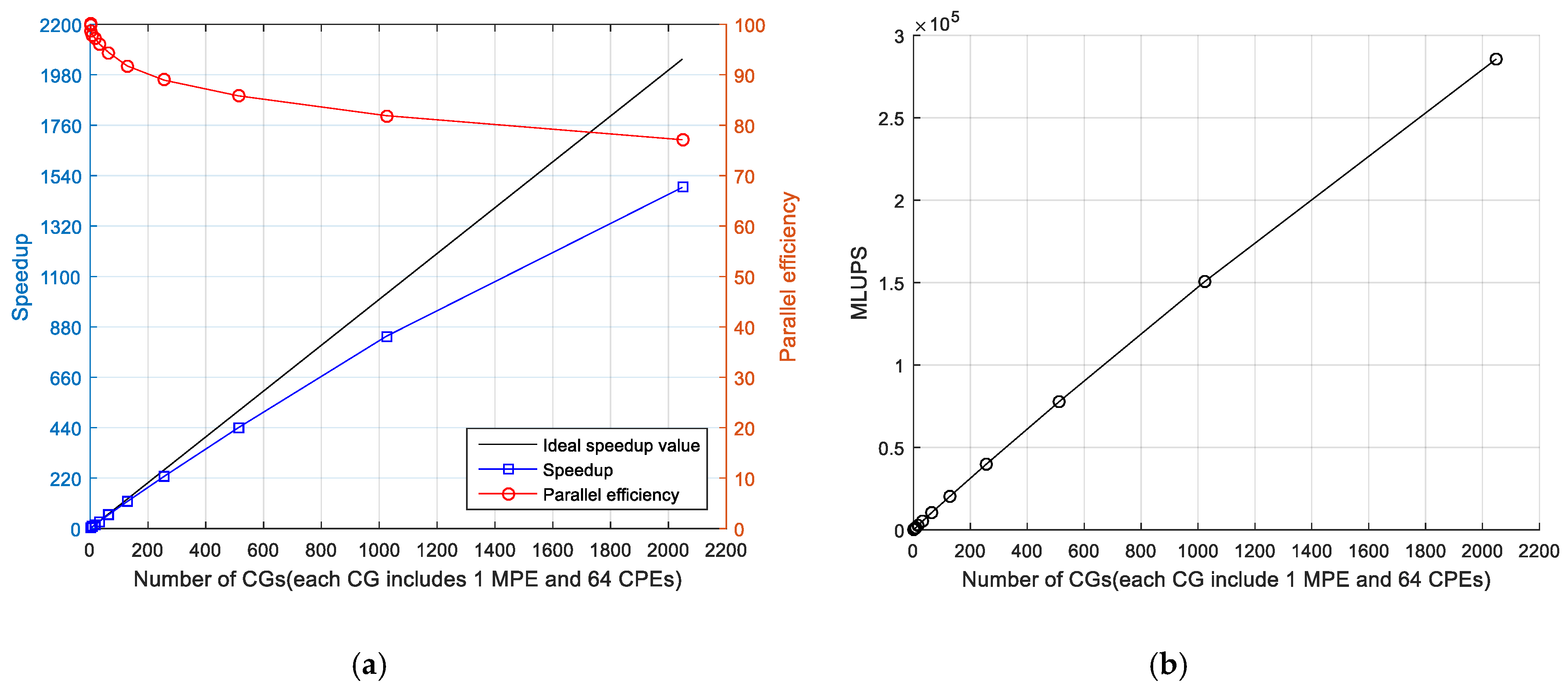
4.2.1. Parallel Efficiency
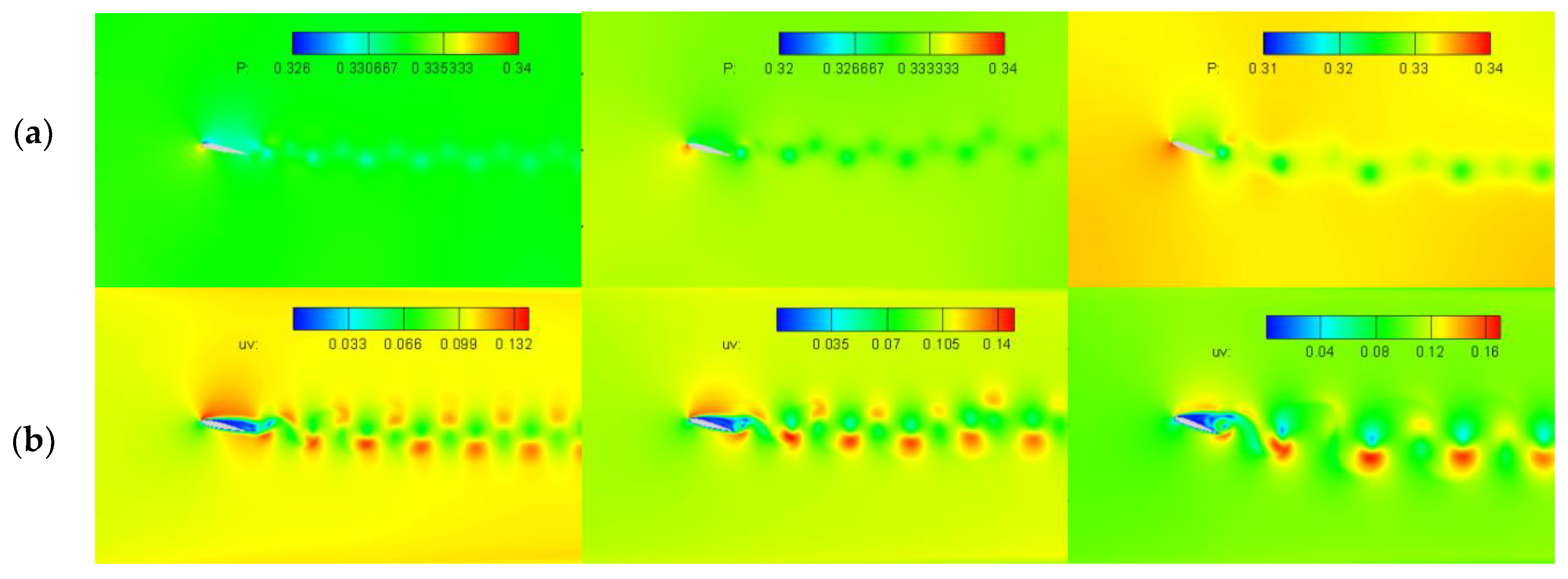
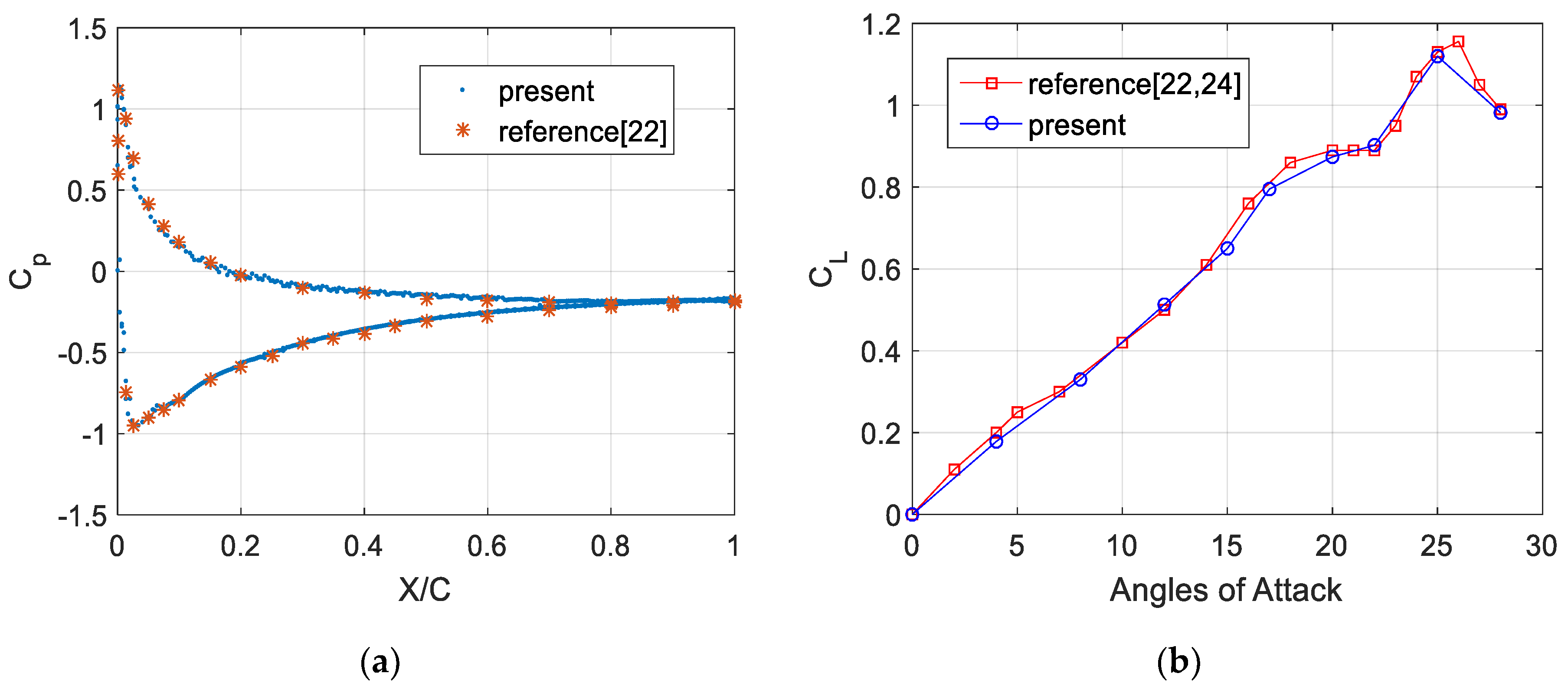
4.2.2. Airfoil Computation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Succi, S. Lattice Boltzmann 2038. EPL 2015, 109, 50001. [Google Scholar] [CrossRef]
- He, Y.; Wang, Y.; Li, Q. Theory and Application of Lattice Boltzmann Method; Science Press: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Guo, S.; Wu, J. Acceleration of lattice Boltzmann simulation via Open ACC. J. Harbin Inst. Technol. 2018, 25, 44–52. [Google Scholar]
- Bartuschat, D.; Rüde, U. A scalable multiphysics algorithm for massively parallel direct numerical simulations of electrophoretic motion. J. Comput. Sci. 2018, 27, 147–167. [Google Scholar] [CrossRef] [Green Version]
- Kutscher, K.; Geier, M.; Krafczyk, M. Multiscale simulation of turbulent flow interacting with porous media based on a massively parallel implementation of the cumulant lattice Boltzmann method. Comput. Fluids 2018. [Google Scholar] [CrossRef]
- Wittmanna, M.; Haagb, V.; Zeisera, T.; Köstlerb, H.; Welleinc, G. Lattice Boltzmann benchmark kernels as a testbed for performance analysis. Comput. Fluids 2018. [Google Scholar] [CrossRef]
- Wittmann, M.; Hager, G.; Zeiser, T.; Treibig, J.; Wellein, G. Chip-level and multi-node analysis of energy-optimized lattice Boltzmann CFD simulations. Concurr. Comput.-Pract. Exp. 2016, 28, 2295–2315. [Google Scholar] [CrossRef]
- Ho, M.Q.; Obrecht, C.; Tourancheau, B.; de Dinechin, B.D.; Hascoet, J. Improving 3D lattice boltzmann method stencil with asynchronous transfers on many-core processors. In Proceedings of the 2017 IEEE 36th International Performance Computing and Communications Conference (IPCCC), San Diego, CA, USA, 10–12 December 2017; pp. 1–9. [Google Scholar]
- Lintermann, A.; Schlimpert, S.; Grimmen, J.; Günther, C.; Meinke, M.; Schroder, W. Massively parallel grid generation on HPC systems. Comput. Methods Appl. Mech. Eng. 2014, 277, 131–153. [Google Scholar] [CrossRef]
- Song, L.; Nian, Z.; Yuan, C.; Wei, W. Accelerating the Parallelization of Lattice Boltzmann Method by Exploiting the Temporal Locality. In Proceedings of the 2017 IEEE International Symposium on Parallel and Distributed Processing with Applications and 2017 IEEE International Conference on Ubiquitous Computing and Communications (ISPA/IUCC), Guangzhou, China, 12–15 December 2017. [Google Scholar]
- Top500. Available online: www.top500.org (accessed on 28 December 2018).
- Fu, H.; Liao, J.; Yang, J.; Wang, L.; Song, Z.; Huang, X.; Yang, C.; Xue, W.; Liu, F.; Qiao, F.; et al. The Sunway TaihuLight supercomputer: System and applications. Sci. China Inf. Sci. 2016, 59, 072001. [Google Scholar] [CrossRef]
- Li, W.; Li, X.; Ren, J.; Jiang, H. Length to diameter ratio effect on heat transfer performance of simple and compound angle holes in thin-wall airfoil cooling. Int. J. Heat Mass Transf. 2018, 127, 867–879. [Google Scholar] [CrossRef]
- Jafari, M.; Razavi, A.; Mirhosseini, M. Effect of airfoil profile on aerodynamic performance and economic assessment of H-rotor vertical axis wind turbines. Energy 2018, 165, 792–810. [Google Scholar] [CrossRef]
- Cao, Y.; Chao, L.; Men, J.; Zhao, H. The efficiently propulsive performance flapping foils with a modified shape. In Proceedings of the OCEANS 2016-Shanghai, Shanghai, China, 10–13 April 2016; pp. 1–4. [Google Scholar]
- He, X.; Luo, L.S. A proiori derivation of the lattice Boltzmann equation. Phys. Rev. E 1997, 55, 6333–6336. [Google Scholar] [CrossRef]
- He, X.; Luo, L.S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. EPL (Europhys. Lett.) 1992, 17, 479. [Google Scholar] [CrossRef]
- Liu, Z. Improved Lattice Boltzmann Method and Large-Scale Parallel Computing; Shanghai University: Shanghai, China, 2014. (In Chinese) [Google Scholar]
- Di Ilio, G.; Chiappini, D.; Ubertini, S.; Bella, G.; Succi, S. Fluid flow around NACA 0012 airfoil at low-Reynolds numbers with hybrid lattice Boltzmann method. Comput. Fluids 2018, 166, 200–208. [Google Scholar] [CrossRef]
- Ma, Y.; Bi, H.; Gan, R.; Li, X.; Yan, X. New insights into airfoil sail selection for sail-assisted vessel with computational fluid dynamics simulation. Adv. Mech. Eng. 2018, 10, 1687814018771254. [Google Scholar] [CrossRef]
- Liu, Y.; Li, K.; Zhang, J.; Wang, H.; Liu, L. Numerical bifurcation analysis of static stall of airfoil and dynamic stall under unsteady perturbation. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3427–3434. [Google Scholar] [CrossRef]
- Kurtulus, D.F. On the unsteady behavior of the flow around NACA 0012 airfoil with steady external conditions at Re = 1000. Int. J. Micro Air Veh. 2015, 7, 301–326. [Google Scholar] [CrossRef]
- Akbari, M.H.; Price, S.J. Simulation of dynamic stall for a NACA 0012 airfoil using a vortex method. J. Fluids Struct. 2003, 17, 855–874. [Google Scholar] [CrossRef]
- Li, X.M.; Leung, K.; So, R.M.C. One-step aeroacoustics simulation using lattice Boltzmann method. AIAA J. 2016, 44, 78–89. [Google Scholar] [CrossRef]
- Orselli, R.M.; Carmo, B.S.; Queiroz, R.L. Noise predictions of the advanced noise control fan model using lattice Boltzmann method and Ffowcs Williams–Hawkings analogy. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 34. [Google Scholar] [CrossRef]








| …… do k = kmin, kmax if (mod((k-kmin),corenum)+1.eq.slavecore_id) then j = jmin index = mod((j-jmin),2) + 1 put_reply(mod((j-jmin)+1,2)+1)=1 ! Read in the first batch of data get_reply(index)=0 call athread_get(0,a(imin,j,k), a_slave(imin,index), (imax-imin+1)*4, get_reply(index), 0, 0, 0) call athread_get(0,b(imin,j,k), b_slave(imin,index), (imax-imin+1)*4, get_reply(index), 0, 0, 0) do j = jmin,jmax index = mod((j-jmin),2)+1 next = mod((j-jmin)+1,2)+1 last = next ! Read in the data needed for the next round of calculation if (j.lt.jmax) then get_reply(next)=0 call athread_get(0,a(imin,j+1,k),a_slave(imin,next), (imax-imin+1)*4,get_reply(next),0,0,0) call athread_get(0,b(imin,j+1,k),b_slave(imin,next), (imax-imin+1)*4,get_reply(next),0,0,0) endif do while (get_reply(index).ne.2) enddo ! Wait for the data required for this round of calculation to be read in do i = imin, imax c_slave(i,index)=a_slave(i,index)*a_slave(i,index)+b_slave(I,index)*b_slave(i,index) enddo put_reply(index)=0 call athread_put(0,c_slave(imin,index),c(imin,j,k),(imax-imin+1)*4,put_reply(index),0,0) do while (ptu_reply(last).ne.1) Enddo ! waiting for the last round of data to be written back ! the first round does not have to wait for the direct pass. enddo do while (ptu_reply(index).ne.1) enddo ! waiting for the last batch of data to be written back endif enddo …… |
| CGs | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cores | 65 | 130 | 260 | 520 | 1040 | 2080 | 4160 | 8320 | 16640 | 33280 | 66560 | 133120 |
| Theoretical acceleration ratio | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 |
| acceleration ratio | 1 | 1.9983096 | 3.9549608 | 7.84065056 | 15.6233262 | 30.9049656 | 60.5670289 | 117.7244635 | 228.170942 | 440.4674223 | 841.5104023 | 1492.812774 |
| Parallel efficiency (%) | 100 | 99.915482 | 98.874021 | 98.0081321 | 97.645789 | 96.5780176 | 94.6359827 | 91.9722371 | 89.1292742 | 86.02879342 | 82.17875022 | 72.89124874 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, X.; Zhu, W.; Xu, K.; Wu, W.; Chu, X.; Zhang, W. Accurate Computation of Airfoil Flow Based on the Lattice Boltzmann Method. Appl. Sci. 2019, 9, 2000. https://doi.org/10.3390/app9102000
Wang L, Zhang X, Zhu W, Xu K, Wu W, Chu X, Zhang W. Accurate Computation of Airfoil Flow Based on the Lattice Boltzmann Method. Applied Sciences. 2019; 9(10):2000. https://doi.org/10.3390/app9102000
Chicago/Turabian StyleWang, Liangjun, Xiaoxiao Zhang, Wenhao Zhu, Kangle Xu, Weiguo Wu, Xuesen Chu, and Wu Zhang. 2019. "Accurate Computation of Airfoil Flow Based on the Lattice Boltzmann Method" Applied Sciences 9, no. 10: 2000. https://doi.org/10.3390/app9102000
APA StyleWang, L., Zhang, X., Zhu, W., Xu, K., Wu, W., Chu, X., & Zhang, W. (2019). Accurate Computation of Airfoil Flow Based on the Lattice Boltzmann Method. Applied Sciences, 9(10), 2000. https://doi.org/10.3390/app9102000