Real-Time GPU-Based Digital Image Correlation Sensor for Marker-Free Strain-Controlled Fatigue Testing
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
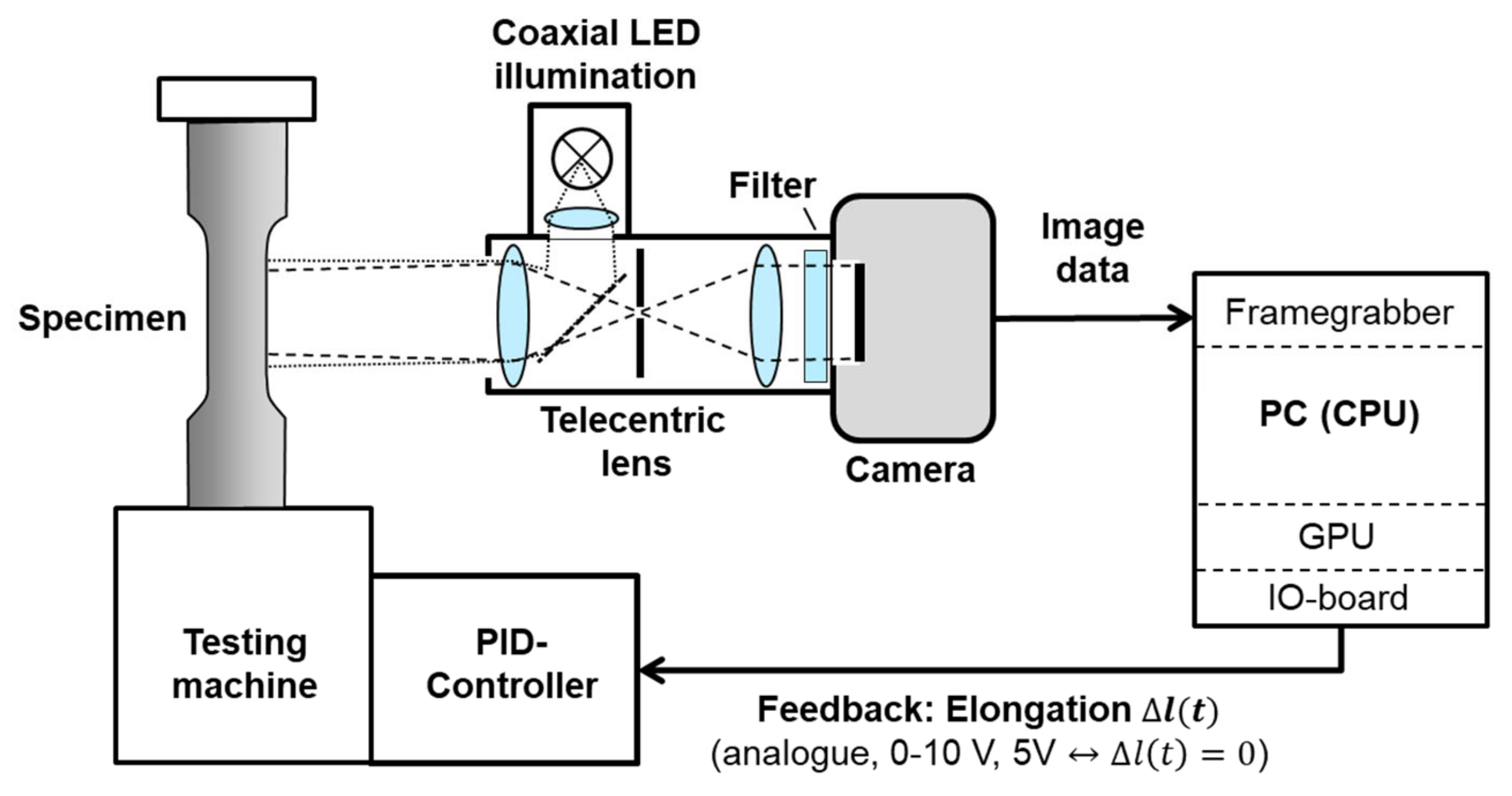
2.1. Sensor Setup and Integration into Materials Testing Setup
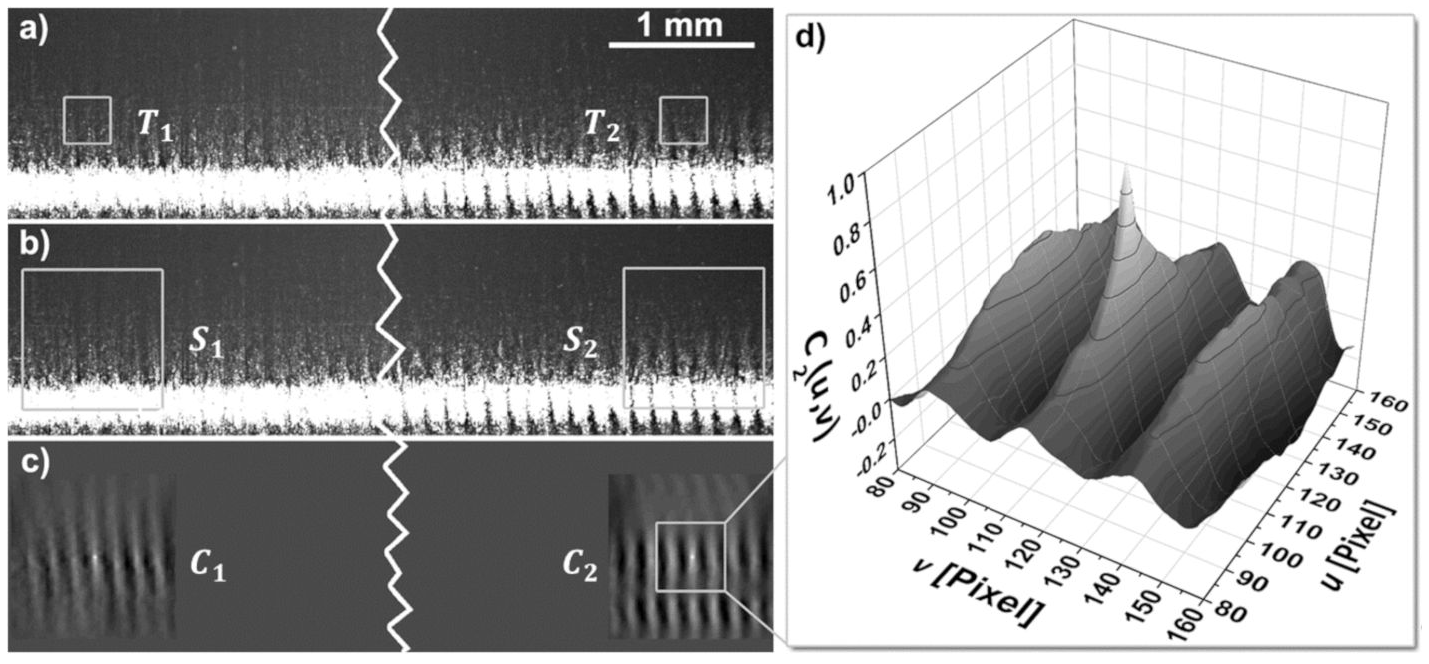
2.2. Real-Time DIC Implementation
3. Results
3.1. Processing Time and Latency for Closed-Loop Control
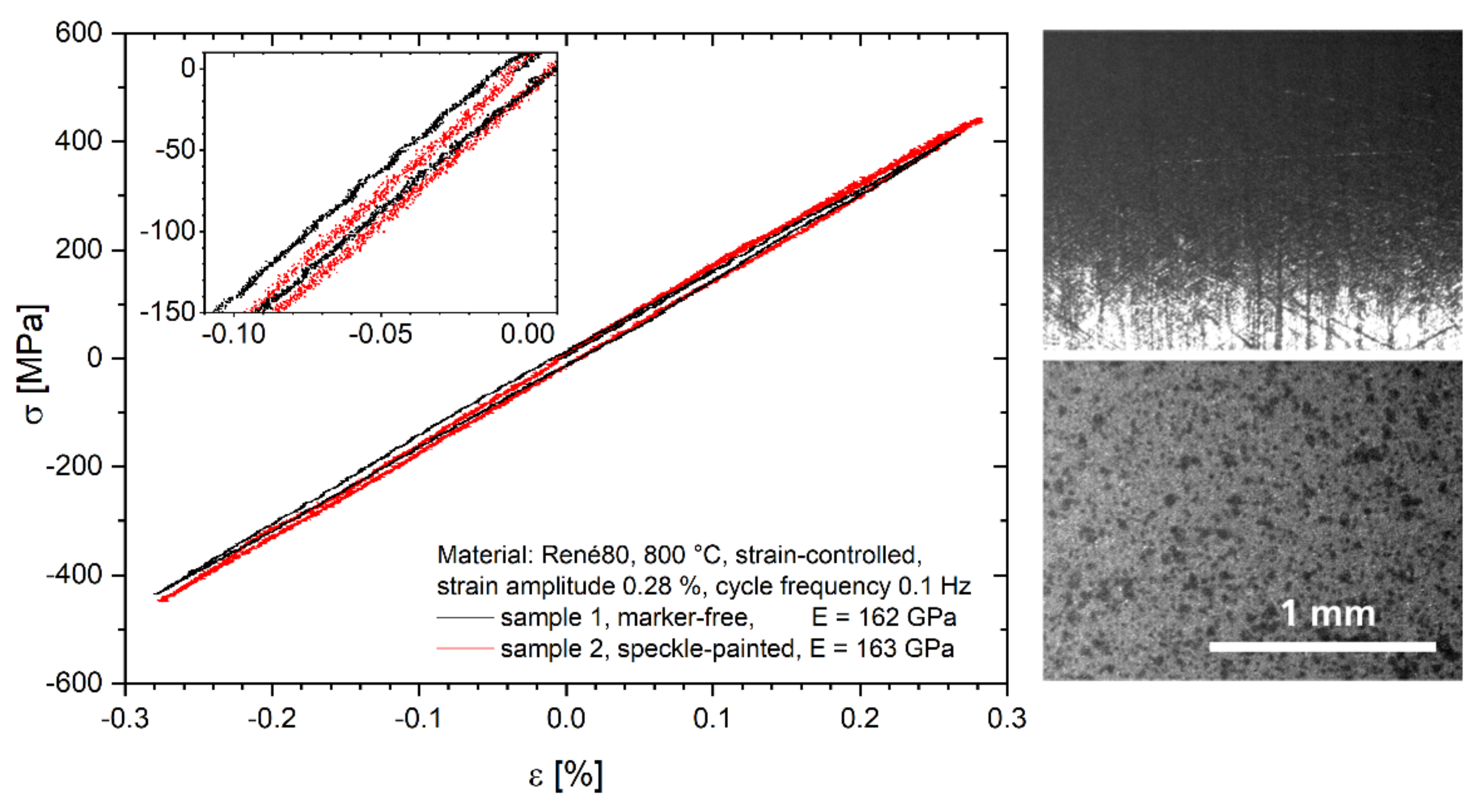
3.2. Comparison to Mechanical Extensometer
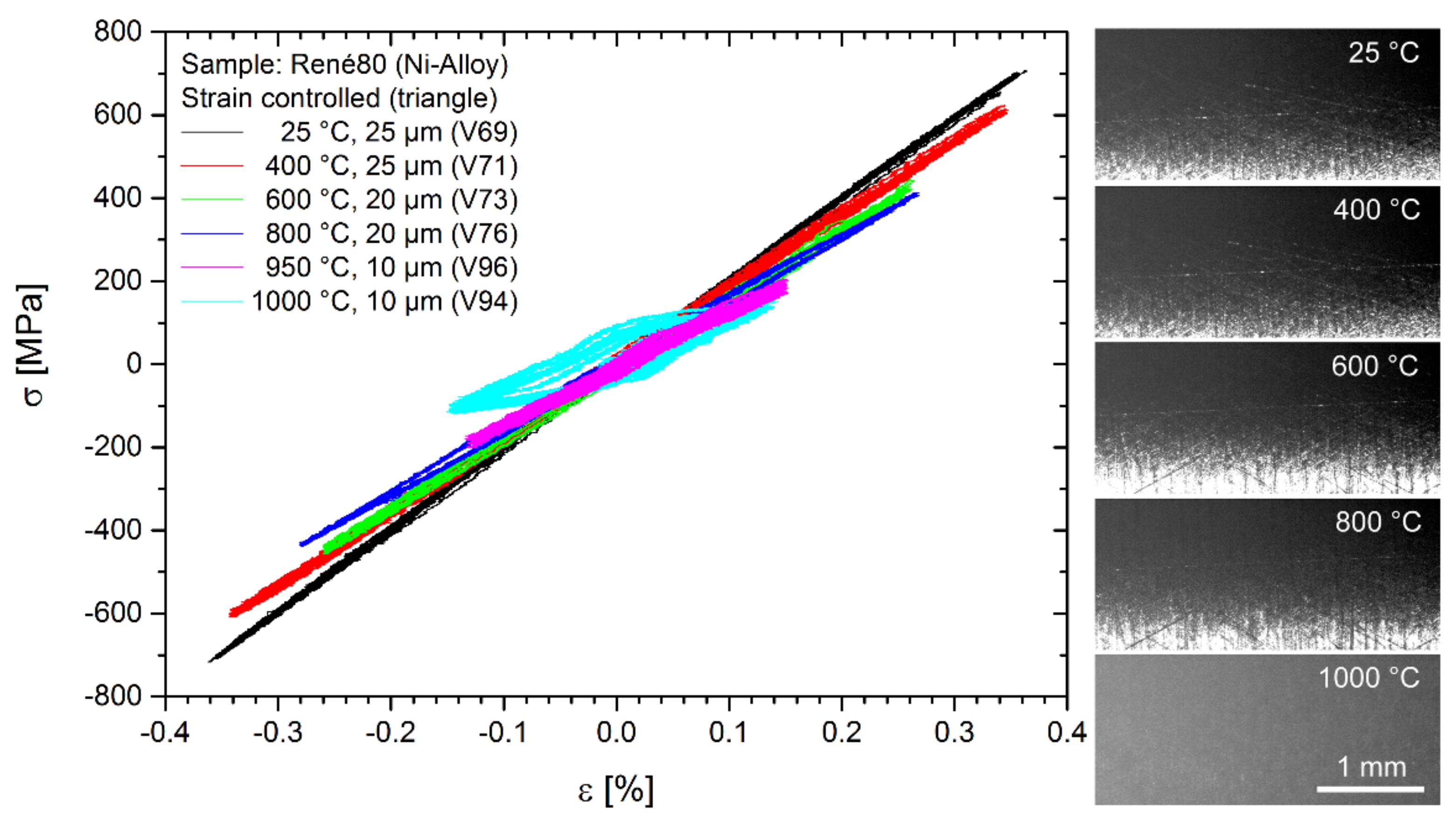
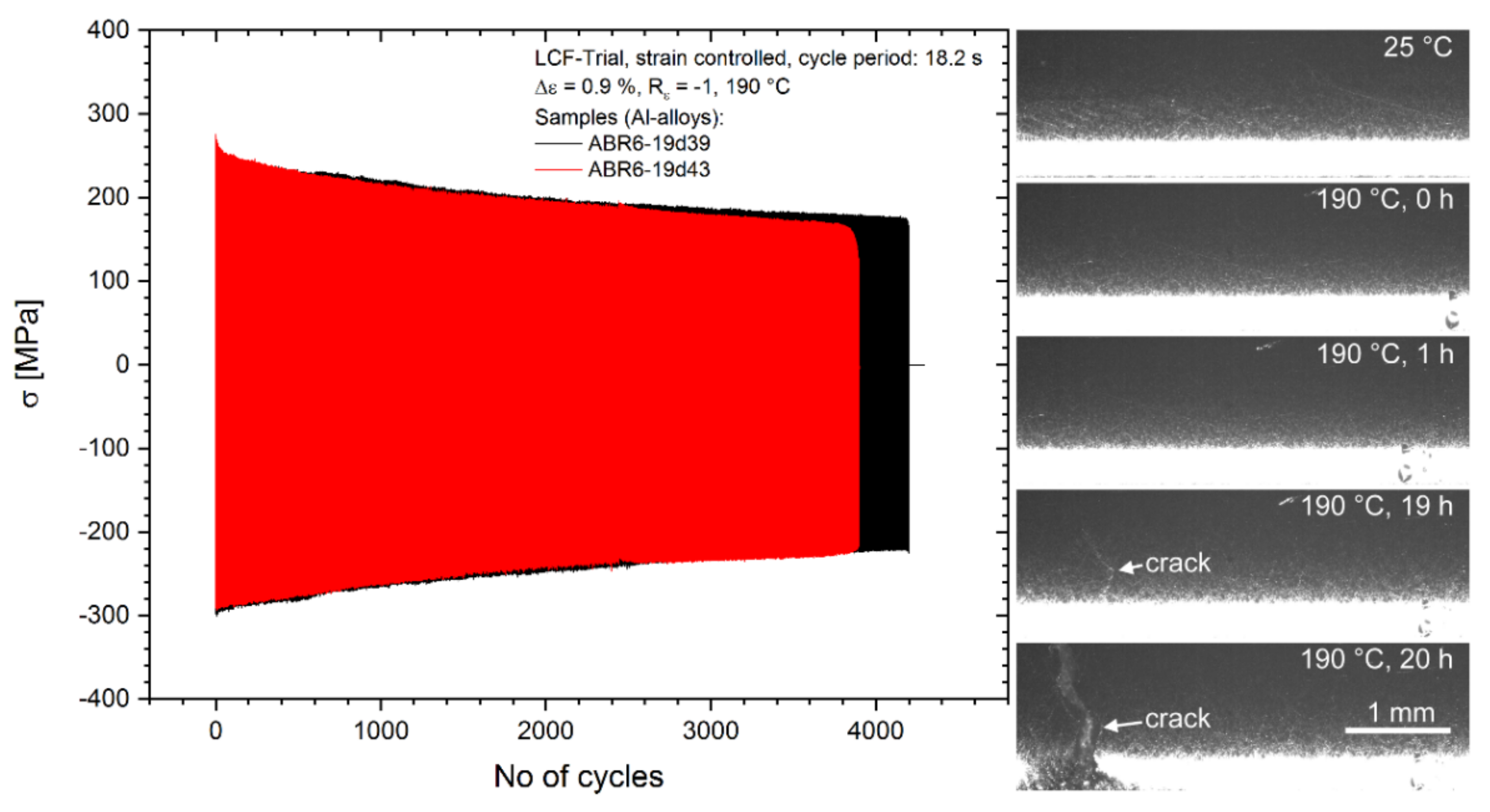
3.3. Strain-Controlled Testing
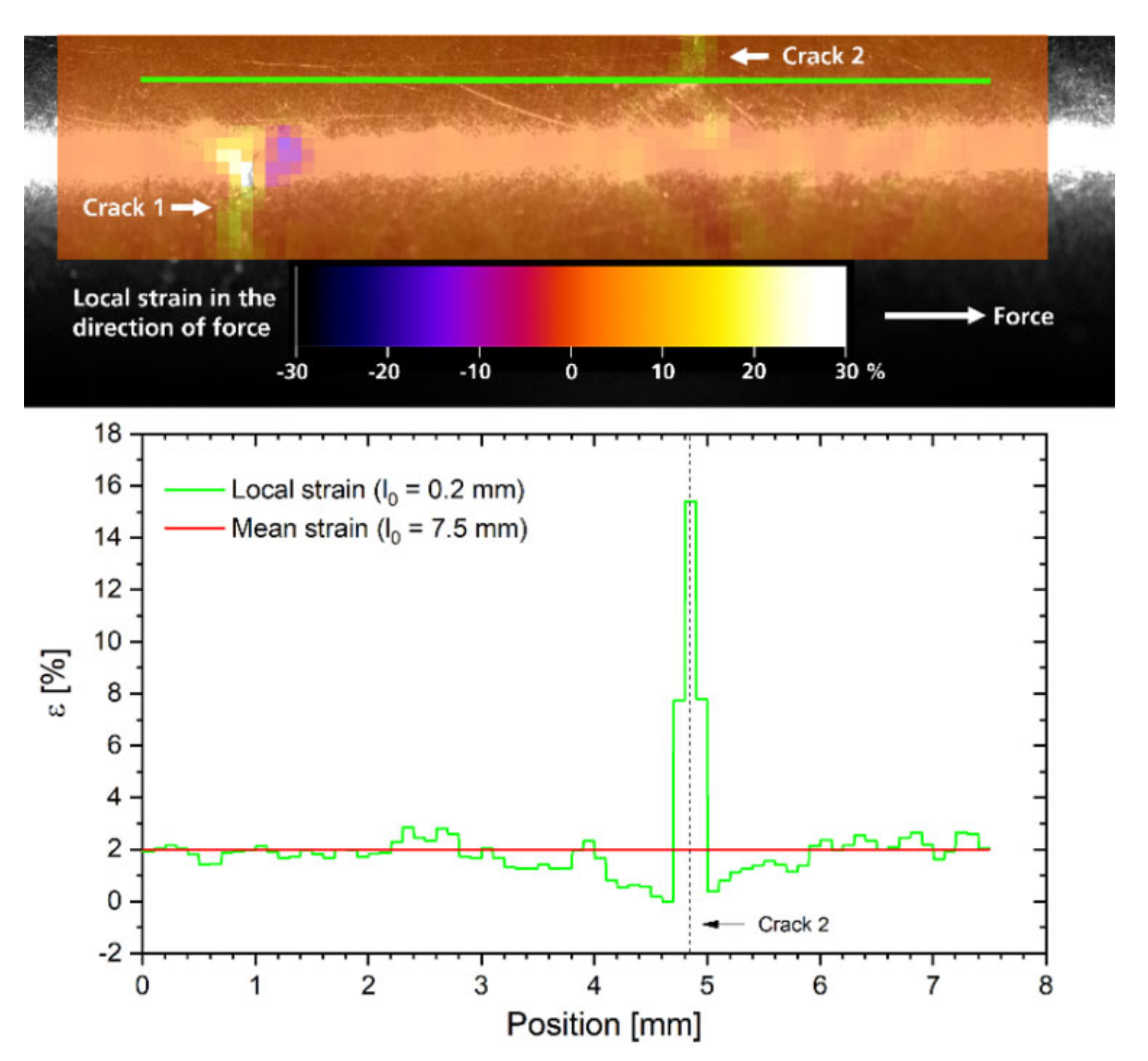
3.4. Real-Time Strain-Field Measurement
4. Discussion
4.1. Sampling Rate and Processing Speed
4.2. Latency
4.3. Marker-Free Measurement
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References and Notes
- ASTM E606/606M: Standard Test Method for Strain-Controlled Fatigue Testing; ASTM International: West Conshohocken, PA, USA, 2012.
- Kanchanomai, C.; Yamamoto, S.; Miyashita, Y.; Mutoh, Y.; McEvily, A.J. Low cycle fatigue test for solders using non-contact digital image measurement system. Int. J. Fatigue 2002, 24, 57–67. [Google Scholar] [CrossRef]
- Zhang, S.; Mao, S.; Arola, D.; Zhang, D. Characterization of the strain-life fatigue properties of thin sheet metal using an optical extensometer. Opt. Lasers Eng. 2014, 60, 44–48. [Google Scholar] [CrossRef]
- Bailey, P.; Higham, M. Application of strain-controlled fatigue testing methods to polymer matrix composites. Procedia Struct. Integr. 2016, 2, 128–135. [Google Scholar] [CrossRef]
- Pan, B.; Tian, L. Advanced video extensometer for non-contact, real-time, high-accuracy strain measurement. Opt. Express 2016, 24, 19082–19093. [Google Scholar] [CrossRef] [PubMed]
- Halama, R.; Gál, P.; Paška, Z.; Sedlák, J.; Vasko, M.; Handrik, M.; Jakubovičová, L.; Kopas, P.; Blatnická, M.; Baniari, V.; et al. A new accelerated technique for validation of cyclic plasticity models. MATEC Web Conf. 2018, 157, 05008. [Google Scholar] [CrossRef]
- Unbehauen, H.; Ley, F. Regelungs- und Steuerungstechnik. In HÜTTE—Das Ingenieurwissen, 34th ed.; Czichos, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kamaya, M.; Kawakubo, M. Mean stress effect on fatigue strength of stainless steel. Int. J. Fatigue 2015, 74, 20–29. [Google Scholar] [CrossRef]
- Eckmann, S.; Schweizer, C. Characterization of fatigue crack growth, damage mechanisms and damage evolution of the nickel-based superalloys MAR-M247 CC (HIP) and CM-247 LC under thermomechanical fatigue loading using in situ optical microscopy. Int. J. Fatigue 2017, 99, 235–241. [Google Scholar] [CrossRef]
- Gupta, S.; Beaudoin, A.J.; Chevy, J. Strain rate jump induced negative strain rate sensitivity (NSRS) in aluminum alloy 2024. Experiments and constitutive modeling. Mater. Sci. Eng. 2017, 683, 143–152. [Google Scholar] [CrossRef]
- Johanson, A.; Viespoli, L.M.; Nyhus, B.; Alvaro, A.; Berto, F.; Hénaff, G. Experimental and numerical investigation of strain distribution of notched lead fatigue test specimen. MATEC Web Conf. 2018, 165, 05003. [Google Scholar] [CrossRef]
- Pan, B.; Wu, D.; Wang, Z.; Xia, Y. High-temperature digital image correlation method for full-field deformation measurement at 1200 °C. Meas. Sci. Technol. 2011, 22, 015701. [Google Scholar] [CrossRef]
- Berke, R.B.; Lambros, J. Ultraviolet digital image correlation (UV-DIC) for high temperature applications. Rev. Sci. Instrum. 2014, 85, 045121. [Google Scholar] [CrossRef]
- Blaber, J.; Adair, B.S.; Antoniou, A. A methodology for high resolution digital image correlation in high temperature experiments. Rev. Sci. Instrum. 2015, 86, 035111. [Google Scholar] [CrossRef]
- Gianola, G.S.; Eberl, C. Micro- and nanoscale tensile testing of materials. JOM J. Miner. Met. Mater. Soc. 2009, 61, 24. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement. A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Schreier, H.; Orteu, J.J.; Sutton, M.A. Image Correlation for Shape, Motion and Deformation Measurements; Springer: Boston, MA, USA, 2009; Chapter 5.5; p. 99. [Google Scholar]
- Xavier, J.; Sousa, A.M.R.; Morais, J.J.L.; Filipe, V.M.J.; Vaz, M. Measuring displacement fields by cross-correlation and a differential technique: Experimental validation. Opt. Eng. 2012, 51, 043602. [Google Scholar] [CrossRef]
- Goos, G. Paralleles Rechnen und Nicht-Analytische Lösungsverfahren; Springer: Berlin, Germany, 1998. [Google Scholar]
- Lu, P.J.; Oki, H.; Frey, C.A.; Chamitoff, G.E.; Chiao, L.; Fincke, E.M.; Foale, C.M.; Magnus, S.H.; McArthur, W.S.; Tani, D.M.; et al. Orders-of-magnitude performance increases in GPU-accelerated correlation of images from the International Space Station. J. Real Time Image Proc. 2010, 5, 179–193. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, T.; Jiang, Z.; Kemao, Q.; Liu, Y.; Liu, Z.; Tang, L.; Dong, S. High accuracy digital image correlation powered by GPU-based parallel computing. Opt. Lasers Eng. 2015, 69, 7–12. [Google Scholar] [CrossRef]
- Wang, T.; Kemao, Q.; Seah, H.S.; Lin, F. A flexible heterogeneous real-time digital image correlation system. Opt. Lasers Eng. 2018, 110, 7–17. [Google Scholar] [CrossRef]
- Thiagu, M.; Subramanian, J.S.; Nasre, R. Fast, sub-pixel accurate digital image correlation algorithm powered by heterogeneous (CPU-GPU) framework. In Advancement of Optical Methods & Digital Image Correlation in Experimental Mechanics; Conference Proceedings of the Society for Experimental Mechanics Series; Lamberti, L., Lin, M., Furlong, C., Sciammarella, C., Reu, P.L., Eds.; Springer: Cham, Switzerland, 2019; p. 3. [Google Scholar]
- Gautier, N.; Aider, J.L. Real-time planar flow velocity measurements using an optical flow algorithm implemented on GPU. J. Vis. 2015, 18, 277–286. [Google Scholar] [CrossRef]
- Nakabo, Y.; Ishikawa, M.; Toyoda, H.; Mizuno, S. 1 ms column parallel vision system and its application of high speed target tracking. In Proceedings of the 2000 ICRA Millennium Conference, IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; Volume 1, pp. 650–655. [Google Scholar]
- Blug, A.; Abt, F.; Nicolosi, L.; Heider, A.; Weber, R.; Carl, D.; Höfler, H.; Tetzlaff, R. The full penetration hole as a stochastic process: Controlling penetration depth in keyhole laser-welding processes. Appl. Phys. B 2012, 108, 97–107. [Google Scholar] [CrossRef]
- Sylvac Switzerland Crissier, Chemin du Closalet 16, 1023 Crissier, Switzerland
- Sutton, M.A.; Yan, J.H.; Tiwari, V.; Schreier, H.W.; Orteu, J.J. The effect of out-of-plane motion on 2D and 3D digital image correlation measurements. Opt. Lasers Eng. 2008, 46, 746–757. [Google Scholar] [CrossRef]
- Digital Image Correlation and Tracking. Available online: https://uk.mathworks.com/matlabcentral/fileexchange/50994-digital-image-correlation-and-tracking (accessed on 6 April 2019).
- Goodman, J.W. Introduction to Fourier Optics, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- MAYTEC Mess- und Regeltechnik GmbH, Im Haselbusch 16, D-78224 Singen, Germany
- Blug, A.; Regina, D.J.; Eckmann, S.; Senn, M.; Bertz, A.; Carl, D.; Eberl, C. GPU-based digital image correlation system for real-time strain-controlled fatigue and strain field measurement. In Proceedings of the SPIE 2019, 11056-30, Optical Metrology Conference, Munich, Germany, 24–27 June 2019. [Google Scholar]
- Pan, B.; Tian, L. Superfast robust digital image correlation analysis with parallel computing. Opt. Eng. 2015, 54, 034106. [Google Scholar] [CrossRef]
- VIC-Gauge Real-Time Strain Measurement. Specifications VIC-2D 6; Correlated Solutions, Inc.: Irmo, SC, USA. Available online: https://www.correlatedsolutions.com/wp-content/uploads/2014/04/VIC-Gauge-2D-System-Specs.pdf (accessed on 6 April 2019).
- VideoXtens 2-120 HP-High Precision without Contacting; ZwickRoell GmbH & Co. KG: Ulm, Germany. Available online: https://www.zwickroell.com/-/media/files/sharepoint/vertriebsdoku_pi/08_893_videoxtens_2-120_hp_pi_d.pdf (accessed on 6 April 2019).
- Nicolosi, L.; Blug, A.; Abt, F.; Tetzlaff, R.; Höfler, H.; Carl, D. Real time control of laser beam welding processes-reality. In Focal-Plane Sensor-Processor Chips, 1st ed.; Zarándy, A., Ed.; Springer Science+Business Media LLC: New York, NY, USA, 2011. [Google Scholar]



| Mechanical Strain | Correlation Size | |||
|---|---|---|---|---|
| Strain amplitude | Template subset size | |||
| Strain rate | Search subset size | |||
| Mechanical stress | Polynomial fitting | |||
| Standard deviation of | the correlation peak | |||
| row | Subset position in | |||
| Image intensity | focal plane | |||
| Correlation amplitude | Search subset | |||
| Displacement | Template subset | |||
| Extensometer base | Correlation image | |||
| length | coordinates | |||
| Elongation | ||||
| Pan 2015 [33] | Pan 2016 [5] | Wang 2018 [22] Var. 2 | Wang 2018 [22] Var. 4 | This, Strain-Contr. | This, Full-Field | |
|---|---|---|---|---|---|---|
| Processor type | CPU | CPU | CPU + GPU | CPU + GPU | CPU + GPU | CPU + GPU |
| DIC algorithm | IC-GN | IC-GN | FFT-CC + IC-GN | FFT-CC + IC-GN | FFT-CC | FFT-CC |
| Path-dependent | yes | yes | yes | no | no | no |
| Maximum displacement | tracking | tracking | tracking | - | 97-pixel | 112-pixel |
| No of subsets | 29949 | 4 | 9440 | 100 | 8 | 2500 |
| Subset size | 21-pixel (61-pixel) | 41-pixel | 21-pixel | 21-pixel | 61-pixel | 31-pixel |
| Sampling rate | 1.46 Hz (0.24 Hz) | 117 Hz | 30 Hz | 30 Hz | 1200 Hz | 10 Hz |
| Processing rate | 44 kHz (7.2 kHz) | 468 Hz | 283 kHz | 3 kHz | 9.6 kHz | 25 kHz |
| Latency | - | - | - | - | 2 ms | 100 ms |
| Marker-free | no | no | no | no | yes | yes |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blug, A.; Regina, D.J.; Eckmann, S.; Senn, M.; Bertz, A.; Carl, D.; Eberl, C. Real-Time GPU-Based Digital Image Correlation Sensor for Marker-Free Strain-Controlled Fatigue Testing. Appl. Sci. 2019, 9, 2025. https://doi.org/10.3390/app9102025
Blug A, Regina DJ, Eckmann S, Senn M, Bertz A, Carl D, Eberl C. Real-Time GPU-Based Digital Image Correlation Sensor for Marker-Free Strain-Controlled Fatigue Testing. Applied Sciences. 2019; 9(10):2025. https://doi.org/10.3390/app9102025
Chicago/Turabian StyleBlug, Andreas, David Joel Regina, Stefan Eckmann, Melanie Senn, Alexander Bertz, Daniel Carl, and Chris Eberl. 2019. "Real-Time GPU-Based Digital Image Correlation Sensor for Marker-Free Strain-Controlled Fatigue Testing" Applied Sciences 9, no. 10: 2025. https://doi.org/10.3390/app9102025
APA StyleBlug, A., Regina, D. J., Eckmann, S., Senn, M., Bertz, A., Carl, D., & Eberl, C. (2019). Real-Time GPU-Based Digital Image Correlation Sensor for Marker-Free Strain-Controlled Fatigue Testing. Applied Sciences, 9(10), 2025. https://doi.org/10.3390/app9102025




