Fault Classification of Rotary Machinery Based on Smooth Local Subspace Projection Method and Permutation Entropy
Abstract
:1. Introduction
2. The Theory of the Smooth Local Subspace Projection Noise Reduction and PE
2.1. The Theory of Smooth Local Subspace Projection Noise Reduction Method
2.2. Local Projection Subspace
2.3. SOD and Data Projection
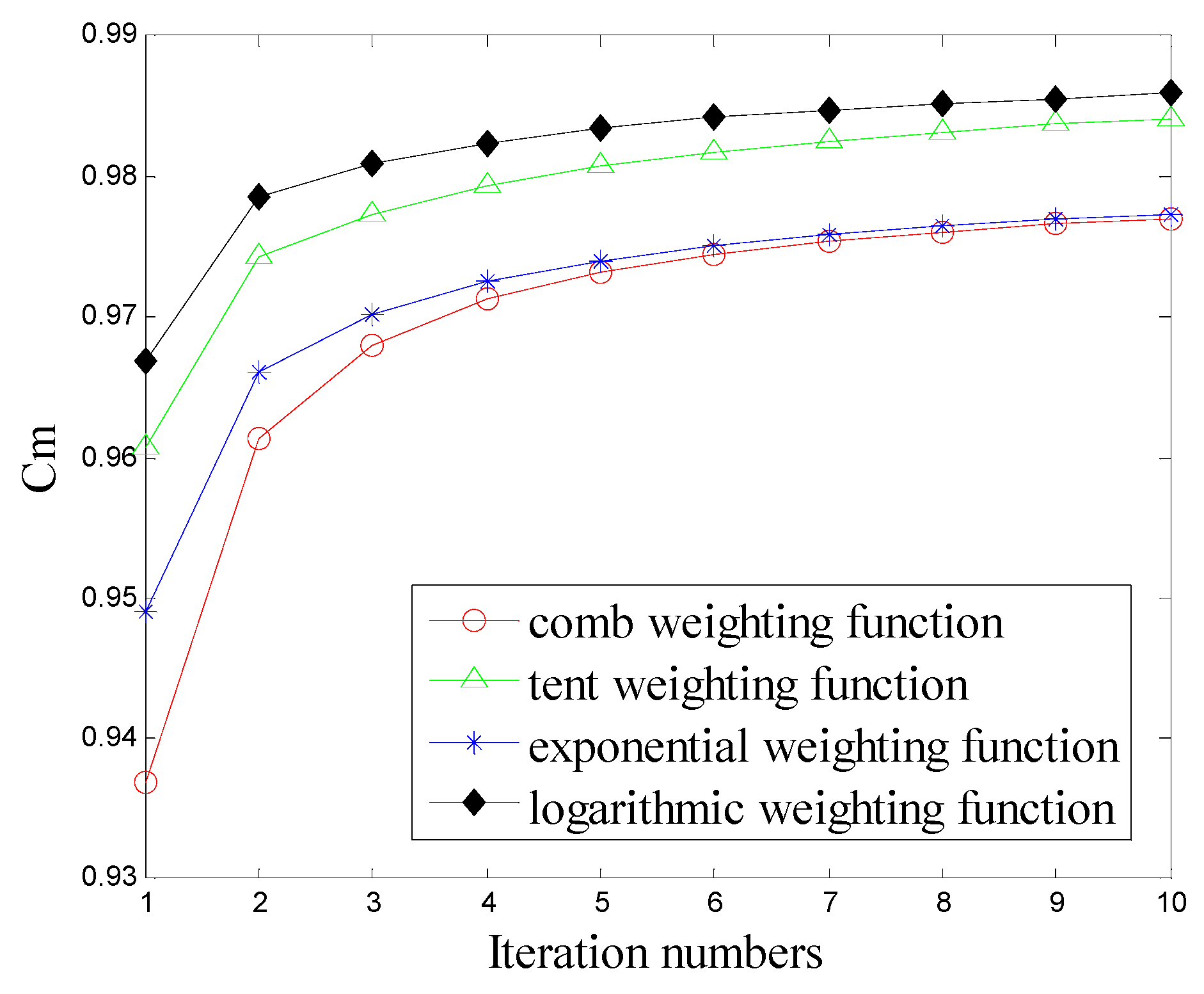
2.4. Smooth Local Subspace Projection Method
2.5. Definition of PE
2.6. Proposed Fault Classification Method Based on the Smooth Local Subspace Projection Denoising Method and PE
3. Numerical Experiments
3.1. Lorenz Signal Simulation Research
3.2. FM Signal Simulation Research
3.3. Simulation Research of PE
4. Applications to Gear and Bearing Fault Classification
4.1. Application to Processing of Case Western Reserve University Bearing Data
4.2. Application to Drivetrain Diagnostics Simulator
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Caesarendra, W.; Pratama, M.; Kosasih, B.; Tjahjowidodo, T.; Glowacz, A. Parsimonious Network Based on a Fuzzy Inference System (PANFIS) for Time Series Feature Prediction of Low Speed Slew Bearing Prognosis. Appl. Sci. 2018, 8, 2656. [Google Scholar] [CrossRef]
- Yuan, N.; Yang, W.; Kang, B.; Xu, S.; Wang, X. Laplacian Eigenmaps Feature Conversion and Particle Swarm Optimization-Based Deep Neural Network for Machine Condition Monitoring. Appl. Sci. 2019, 8, 2611. [Google Scholar] [CrossRef]
- Kuai, M.; Cheng, G.; Pang, Y.; Li, Y. Research of Planetary Gear Fault Diagnosis Based on Permutation Entropy of CEEMDAN and ANFIS. Sensors 2018, 18, 782. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Shi, W. Fault Diagnosis of Rotating Machinery Based on the Multiscale Local Projection Method and Diagonal Slice Spectrum. Appl. Sci. 2018, 8, 619. [Google Scholar] [CrossRef]
- Bozchalooi, I.S.; Liang, M. A joint resonance frequency estimation and in-band noise reduction method for enhancing the detectability of bearing fault signals. Mech. Syst. Signal Process. 2008, 22, 915–933. [Google Scholar] [CrossRef]
- Arnel, H.; Brown, R.; Kadtke, J. Prediction and system identification in chaotic nonlinear systems: Time series with broadband spectra. Phys. Lett. A 1989, 138, 401–408. [Google Scholar]
- Lee, S.K.; White, P.R. The enhancement of impulsive noise and vibration signals for fault detection in rotating and reciprocating machinery. J. Sound Vib. 1998, 217, 485–505. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Y.; Song, G. Detection of High-Strength Bolts Looseness Using Lead Zirconate Titanate Due to Wavelet Packet Analysis. Earth Sp. 2018, 1069. [Google Scholar] [CrossRef]
- Yang, W.; Kong, Q.; Ho SC, M.; Mo, Y.L.; Song, G. Real-Time Monitoring of Soil Compaction Using Piezoceramic-Based Embeddable Transducers and Wavelet Packet Analysis. IEEE Access 2018, 6, 5208–5214. [Google Scholar] [CrossRef]
- Chen, X.; Ma, D. Mode Separation for Multimodal Ultrasonic Lamb Waves Using Dispersion Compensation and Independent Component Analysis of Forth-Order Cumulant. Appl. Sci. 2019, 9, 555. [Google Scholar] [CrossRef]
- Fang, L.; Sun, H. Study on EEMD-Based KICA and Its Application in Fault-Feature Extraction of Rotating Machinery. Appl. Sci. 2018, 8, 1441. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Song, G. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Yuan, R.; Lv, Y.; Song, G. Multi-fault diagnosis of rolling bearings via adaptive projection intrinsically transformed multivariate empirical mode decomposition and high order singular value decomposition. Sensors 2018, 18, 1210. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.F.; Li, Y.B.; Luo, Z.G. Fault classification of rolling bearing based on reconstructed phase space and Gaussian mixture model. J. Sound Vib. 2009, 323, 1077–1089. [Google Scholar] [CrossRef]
- Liang, L.; Shan, L.; Liu, F.; Niu, B.; Xu, G. Sparse Envelope Spectra for Feature Extraction of Bearing Faults Based on NMF. Appl. Sci. 2019, 9, 755. [Google Scholar] [CrossRef]
- Zhang, Y.; Tong, S.; Cong, F.; Xu, J. Research of feature extraction method based on sparse reconstruction and multiscale dispersion entropy. Appl. Sci. 2018, 8, 888. [Google Scholar] [CrossRef]
- Ma, Z.; Wen, G.; Jiang, C. EEMD independent extraction for mixing features of rotating machinery reconstructed in phase space. Sensors 2015, 15, 8550–8569. [Google Scholar] [CrossRef] [PubMed]
- Tufillaro, N.B.; Abbot, T.; Reilly, J.; Hickey, F.R. An experimental approach to nonlinear dynamics and chaos. Am. J. Phys. 1993, 61, 958–959. [Google Scholar] [CrossRef]
- Siegel, S.G.; Seidel, J.; Fagley, C.; Luchtenburg, D.M.; Cohen, K.; McLaughlin, T. Low-dimensional modelling of a transient cylinder wake using double proper orthogonal decomposition. J. Fluid Mech. 2008, 610, 1–42. [Google Scholar] [CrossRef]
- Galvanetto, U.; Violaris, G. Numerical investigation of a new damage detection method based on proper orthogonal decomposition. Mech. Syst. Signal Process. 2007, 21, 1346–1361. [Google Scholar] [CrossRef]
- Volkwein, S. Model Reduction Using Proper Orthogonal Decomposition. 2008. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.483.4636&rep=rep1&type=pdf (accessed on 15 May 2019).
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 2012; pp. 137–138. [Google Scholar]
- Acharjee, S.; Zabaras, N. A concurrent model reduction approach on spatial and random domains for the solution of stochastic PDEs. Int. J. Numer. Methods Eng. 2006, 66, 1934–1954. [Google Scholar] [CrossRef]
- Van Belzen, F.; Weiland, S. Reconstruction and approximation of multidimensional signals described by proper orthogonal decompositions. IEEE Trans. Signal Process. 2008, 56, 576–587. [Google Scholar] [CrossRef]
- Wang, D.; Xiang, W.; Zeng, P.; Zhu, H. Damage identification in shear-type structures using a proper orthogonal decomposition approach. J. Sound Vib. 2015, 355, 135–149. [Google Scholar] [CrossRef]
- Lenaerts, V.; Kerschen, G.; Golinval, J.C. Identification of a continuous structure with a geometrical non-linearity, part ii: proper orthogonal decomposition. J. Sound Vib. 2003, 262, 907–919. [Google Scholar] [CrossRef]
- Gedalyahu, K.; Eldar, Y.C. Time-delay estimation from low-rate samples: a union of subspaces approach. IEEE Trans. Signal Process. 2010, 58, 3017–3031. [Google Scholar] [CrossRef]
- Chelidze, D.; Zhou, W. Smooth orthogonal decomposition-based vibration mode identification. J. Sound Vib. 2006, 292, 461–473. [Google Scholar] [CrossRef]
- Farooq, U.; Feeny, B.F. Smooth orthogonal decomposition for modal analysis of randomly excited systems. J. Sound Vib. 2008, 316, 137–146. [Google Scholar] [CrossRef] [Green Version]
- Chelidze, D.; Chelidze, G. Nonlinear Model Reduction Based on Smooth Orthogonal Decomposition; Iasted International Conference on Control & Applications ACTA Press: Anaheim, CA, USA, 2007; pp. 325–330. [Google Scholar]
- Lee, J.; Wang, J.; Zhang, C.; Bian, Z. Visual object recognition using probabilistic kernel subspace similarity. Pattern Recognit. 2005, 38, 997–1008. [Google Scholar] [CrossRef]
- Liu, Z.S.; Chen, S.H. Eigenvalue and eigenvector derivatives of nonlinear eigenproblems. J. Guid. Control Dyn. 2012, 16, 788–789. [Google Scholar] [CrossRef]
- Chen, B.S.; Lee, B.K.; Guo, L.B. Optimal tracking design for stochastic fuzzy systems. IEEE Trans. Fuzzy Syst. 2003, 11, 796–813. [Google Scholar] [CrossRef]
- Chelidze, D. Smooth local subspace projection for nonlinear noise reduction. Chaos 2014, 24, 274–276. [Google Scholar] [CrossRef] [PubMed]
- Christoph, B.; Bernd, P. Permutation entropy: a natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar]
- Theodossiades, S.; Natsiavas, S. Non-linear dynamics of gear-pair systems with periodic stiffness and backlash. J. Sound Vib. 2000, 229, 287–310. [Google Scholar] [CrossRef]
- Zhang, J.; Tao, Z. Parameter-induced stochastic resonance based on spectral entropy and its application to weak signal detection. Rev. Sci. Instrum. 2015, 86, 025005. [Google Scholar] [CrossRef] [PubMed]
- Lv, Y.; Yuan, R.; Wang, T.; Li, H.; Song, G. Health degradation monitoring and early fault diagnosis of a rolling bearing based on CEEMDAN and improved MMSE. Materials 2018, 11, 1009. [Google Scholar] [CrossRef]
- Xie, Z.; Xiong, J.; Zhang, D.; Wang, T.; Shao, Y.; Huang, W. Design and Experimental Investigation of a Piezoelectric Rotation Energy Harvester Using Bistable and Frequency Up-Conversion Mechanisms. Appl. Sci. 2018, 8, 1418. [Google Scholar] [CrossRef]
- Du, C.; Zou, D.; Liu, T.; Li, W. A Study on the Influence of Stage Load on Health Monitoring of Axial Concrete Members Using Piezoelectric Based Smart Aggregate. Appl. Sci. 2018, 8, 423. [Google Scholar] [CrossRef]
- Xu, K.; Deng, Q.; Cai, L.; Ho, S.; Song, G. Damage detection of a concrete column subject to blast loads using embedded piezoceramic transducers. Sensors 2018, 18, 1377. [Google Scholar] [CrossRef]
- Wang, F.; Huo, L.; Song, G. A piezoelectric active sensing method for quantitative monitoring of bolt loosening using energy dissipation caused by tangential damping based on the fractal contact theory. Smart Mat. Struct. 2017, 27, 015023. [Google Scholar] [CrossRef]
- Karagiannidis, G.K. A closed-form solution for the distribution of the sum of Nakagami-m random phase vectors. IEEE Commun. Lett. 2006, 10, 828–830. [Google Scholar] [CrossRef]
- Thomas, R.D.; Moses, N.C.; Semple, E.A.; Strang, A.J. An efficient algorithm for the computation of average mutual information: validation and implementation in Matlab. J. Math. Psychol. 2014, 61, 45–59. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [Green Version]
- Fan, H.; Wen, C. Two-dimensional adaptive filtering based on projection algorithm. IEEE Trans. Signal Process. 2004, 52, 832–838. [Google Scholar] [CrossRef]
- Yuan, R.; Lv, Y.; Song, G. Fault Diagnosis of Rolling Bearing Based on a Novel Adaptive High-Order Local Projection Denoising Method. Complexity 2018, 1–15. [Google Scholar] [CrossRef]
- Yadav, R.S.; Dwivedi, S.; Mittal, A.K. Prediction rules for regime changes and length in a new regime for the Lorenz model. J. Atmos. Sci. 2005, 62, 2316–2321. [Google Scholar] [CrossRef]
- Fei, J.; Zhong, L. Study on continuous chaotic frequency modulation signals. In Proceedings of the 2008 International Symposium on Information Science and Engineering, Shanghai, China, 20–22 December 2008; pp. 350–353. [Google Scholar]
- Lv, Y.; Zhu, Q.; Yuan, R. Fault diagnosis of rolling bearing based on fast nonlocal means and envelop spectrum. Sensors 2015, 15, 1182–1198. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Shen, C.; Chen, L. Deep fault recognizer: An integrated model to denoise and extract features for fault diagnosis in rotating machinery. Appl. Sci. 2017, 7, 41. [Google Scholar] [CrossRef]
- Balakrishnan, A.V.; Mazumdar, R.R. On powers of gaussian white noise. IEEE Trans. Inf. Theory 2010, 57, 7629–7634. [Google Scholar] [CrossRef]
- Loparo, K.A. Bearings Vibration Data Set, Case Western Reserve University. Available online: http://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 15 May 2018).


































| (1) Embedding of delay coordinates |
|
(2) SOD processing
|
(3) Shifting and repeating
|
| SNR of Added Noise | SNR | Cm | MSE | |||
|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | |
| −1 | −1 | 7.216 | 0.681 | 0.718 | 0.289 | 0.179 |
| −0.1 | −0.1 | 9.725 | 0.750 | 0.807 | 0.243 | 0.127 |
| 1 | 1 | 11.645 | 0.837 | 0.894 | 0.189 | 0.071 |
| 2 | 2 | 12.730 | 0.934 | 0.971 | 0.145 | 0.047 |
| Rolling Element Bearing Parameters of 6205-2RS JEM SKF (Diameter/mm) | |||||
|---|---|---|---|---|---|
| Ball number n | Contact angle α | Ball diameter dr | Outside diameter d2 | Inside diameter d1 | Pitch diameter Dw |
| 9 | 0 | 7.9 | 52 | 25 | 46.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, L.; Lv, Y.; Fu, G. Fault Classification of Rotary Machinery Based on Smooth Local Subspace Projection Method and Permutation Entropy. Appl. Sci. 2019, 9, 2102. https://doi.org/10.3390/app9102102
Xiao L, Lv Y, Fu G. Fault Classification of Rotary Machinery Based on Smooth Local Subspace Projection Method and Permutation Entropy. Applied Sciences. 2019; 9(10):2102. https://doi.org/10.3390/app9102102
Chicago/Turabian StyleXiao, Lingjun, Yong Lv, and Guozi Fu. 2019. "Fault Classification of Rotary Machinery Based on Smooth Local Subspace Projection Method and Permutation Entropy" Applied Sciences 9, no. 10: 2102. https://doi.org/10.3390/app9102102
APA StyleXiao, L., Lv, Y., & Fu, G. (2019). Fault Classification of Rotary Machinery Based on Smooth Local Subspace Projection Method and Permutation Entropy. Applied Sciences, 9(10), 2102. https://doi.org/10.3390/app9102102





