Scaling of Three-Dimensional Computer-Generated Holograms with Layer-Based Shifted Fresnel Diffraction
Abstract
:1. Introduction
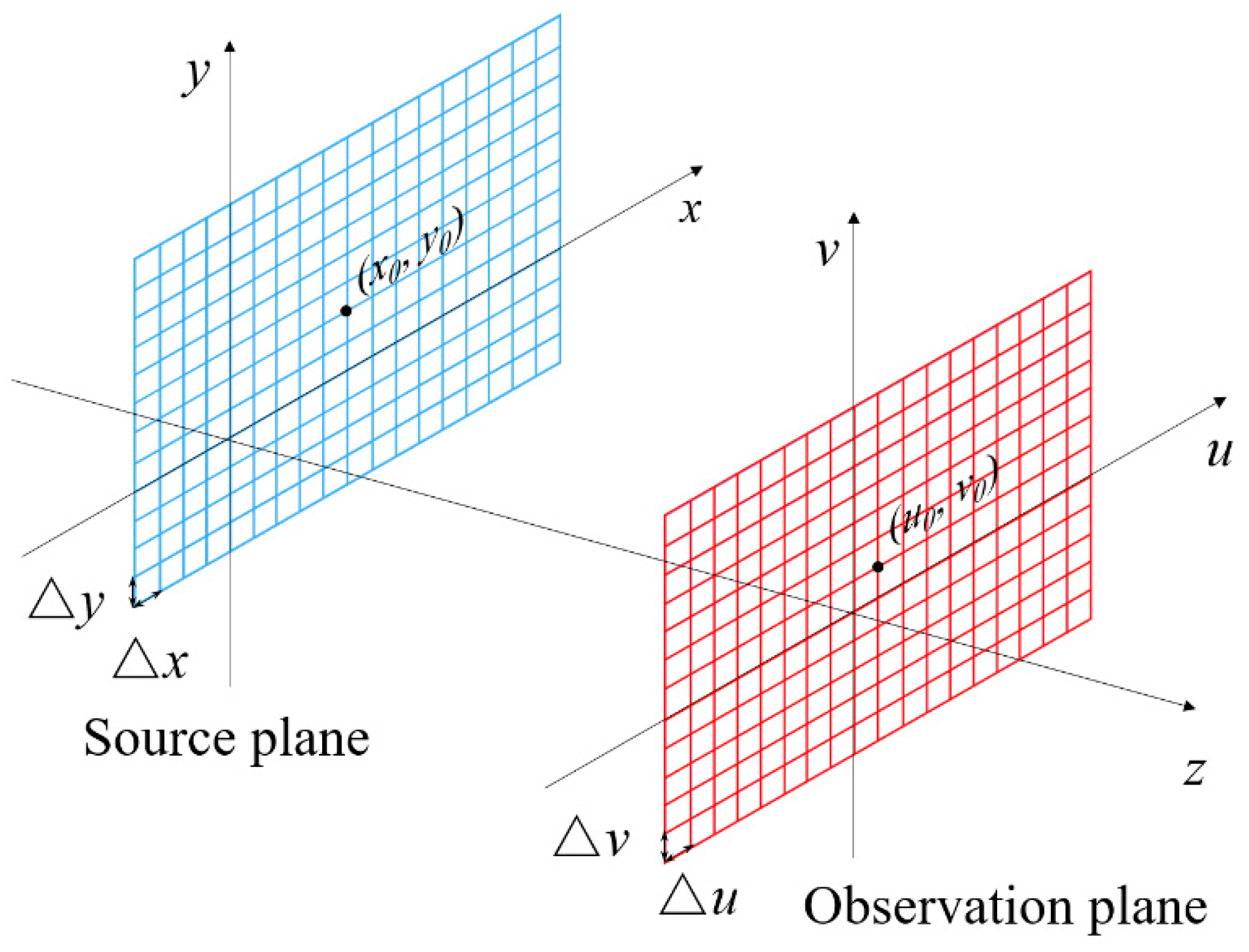
2. Layer-Based Shifted Fresnel Diffraction
3. Reconstruction Results
4. Accuracy Analysis with Different Sampling Parameters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Benton, S.A.; Bove, V.M. Holographic Imaging; Wiley-Interscience: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zhang, H.; Zhao, Y.; Cao, L.; Jin, G. Three-dimensional display technologies in wave and ray optics: A review. Chin. Opt. Lett. 2014, 12, 060002. [Google Scholar] [CrossRef]
- Lucente, M.E. Interactive computation of holograms using a look-up table. ELECTIM 1993, 2, 28–34. [Google Scholar] [CrossRef]
- Matsushima, K. Computer-generated holograms for three-dimensional surface objects with shade and texture. Appl. Opt. 2005, 44, 4607–4614. [Google Scholar] [CrossRef]
- Ahrenberg, L.; Benzie, P.; Magnor, M.; Watson, J. Computer generated holograms from three dimensional meshes using an analytic light transport model. Appl. Opt. 2008, 47, 1567–1574. [Google Scholar] [CrossRef]
- Kim, H.; Hahn, J.; Lee, B. Mathematical modeling of triangle-mesh-modeled three-dimensional surface objects for digital holography. Appl. Opt. 2008, 47, D117–D127. [Google Scholar] [CrossRef] [Green Version]
- Fan, F.; Jiang, X.; Yan, X.; Wen, J.; Chen, S.; Zhang, T.; Han, C. Holographic Element-Based Effective Perspective Image Segmentation and Mosaicking Holographic Stereogram Printing. Appl. Sci. 2019, 9, 920. [Google Scholar] [CrossRef]
- Wakunami, K.; Yamaguchi, M. Calculation for computer generated hologram using ray-sampling plane. Opt. Express 2011, 19, 9086–9101. [Google Scholar] [CrossRef]
- Kang, H.; Stoykova, E.; Yoshikawa, H. Fast phase-added stereogram algorithm for generation of photorealistic 3D content. Appl. Opt. 2016, 55, A135–A143. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, Y.; Cao, L.C.; Jin, G.F. Fully computed holographic stereogram based algorithm for computer-generated holograms with accurate depth cues. Opt. Express 2015, 23, 3901–3913. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, Y.; Cao, L.; Jin, G. Layered holographic stereogram based on inverse Fresnel diffraction. Appl. Opt. 2016, 55, A154–A159. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, L.; Jin, G. Three-dimensional computer-generated hologram with Fourier domain segmentation. Opt. Express 2019, 27, 11689–11697. [Google Scholar] [CrossRef]
- Chen, J.S.; Chu, D.P. Improved layer-based method for rapid hologram generation and real-time interactive holographic display applications. Opt. Express 2015, 23, 18143–18155. [Google Scholar] [CrossRef]
- Bayraktar, M.; Özcan, M. Method to calculate the far field of three-dimensional objects for computer-generated holography. Appl. Opt. 2010, 49, 4647–4654. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, L.; Jin, G. Computer-generated hologram with occlusion effect using layer-based processing. Appl. Opt. 2017, 56, F138–F143. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, L.; Zhang, H.; Kong, D.; Jin, G. Accurate calculation of computer-generated holograms using angular-spectrum layer-oriented method. Opt. Express 2015, 23, 25440–25449. [Google Scholar] [CrossRef]
- Voelz, D.G. Computational Fourier Optics: A MATLAB Tutorial; SPIE Press: Bellingham, WA, USA, 2011. [Google Scholar]
- Zhang, F.; Yamaguchi, I.; Yaroslavsky, L.P. Algorithm for reconstruction of digital holograms with adjustable magnification. Opt. Lett. 2004, 29, 1668–1670. [Google Scholar] [CrossRef]
- Okada, N.; Shimobaba, T.; Ichihashi, Y.; Oi, R.; Yamamoto, K.; Oikawa, M.; Kakue, T.; Masuda, N.; Ito, T. Band-limited double-step Fresnel diffraction and its application to computer-generated holograms. Opt. Express 2013, 21, 9192–9197. [Google Scholar] [CrossRef]
- Chang, C.; Wu, J.; Qi, Y.; Yuan, C.; Nie, S.; Xia, J. Simple calculation of a computer-generated hologram for lensless holographic 3D projection using a nonuniform sampled wavefront recording plane. Appl. Opt. 2016, 55, 7988–7996. [Google Scholar] [CrossRef]
- Bluestein, L. A linear filtering approach to the computation of discrete Fourier transform. IEEE Trans. Audio Electroacoust. 1970, 18, 451–455. [Google Scholar] [CrossRef] [Green Version]
- Rabiner, L.; Schafer, R.; Rader, C. The chirp z-transform algorithm. IEEE Trans. Audio Electroacoust. 1969, 17, 86–92. [Google Scholar] [CrossRef]
- Muffoletto, R.P.; Tyler, J.M.; Tohline, J.E. Shifted Fresnel diffraction for computational holography. Opt. Express 2007, 15, 5631–5640. [Google Scholar] [CrossRef]
- Tomoyoshi, S.; Takashi, K.; Naohisa, O.; Minoru, O.; Yumi, Y.; Tomoyoshi, I. Aliasing-reduced Fresnel diffraction with scale and shift operations. J. Opt. 2013, 15, 075405. [Google Scholar]
- Shimobaba, T.; Makowski, M.; Kakue, T.; Oikawa, M.; Okada, N.; Endo, Y.; Hirayama, R.; Ito, T. Lensless zoomable holographic projection using scaled Fresnel diffraction. Opt. Express 2013, 21, 25285–25290. [Google Scholar] [CrossRef]
- Restrepo, J.F.; Garcia-Sucerquia, J. Magnified reconstruction of digitally recorded holograms by Fresnel–Bluestein transform. Appl. Opt. 2010, 49, 6430–6435. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, L.; Zong, S.; Jin, G. Zoomable three-dimensional computer-generated holographic display based on shifted Fresnel diffraction. In Proceedings of the SPIE 10022, Holography, Diffractive Optics, and Applications VII, Beijing, China, 31 October 2016; Volune 10022, p. 100221D. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, J.; Liu, J.; Wang, Y. Elimination of a zero-order beam induced by a pixelated spatial light modulator for holographic projection. Appl. Opt. 2009, 48, 5834–5841. [Google Scholar] [CrossRef]
- Zhang, H.; Tan, Q.; Jin, G. Holographic display system of a three-dimensional image with distortion-free magnification and zero-order elimination. Opt. Eng. 2012, 51, 075801. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, L.; Jin, G. Lighting effects rendering in three-dimensional computer-generated holographic display. Opt. Commun. 2016, 370, 192–197. [Google Scholar] [CrossRef]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Cao, L.; Jin, G. Scaling of Three-Dimensional Computer-Generated Holograms with Layer-Based Shifted Fresnel Diffraction. Appl. Sci. 2019, 9, 2118. https://doi.org/10.3390/app9102118
Zhang H, Cao L, Jin G. Scaling of Three-Dimensional Computer-Generated Holograms with Layer-Based Shifted Fresnel Diffraction. Applied Sciences. 2019; 9(10):2118. https://doi.org/10.3390/app9102118
Chicago/Turabian StyleZhang, Hao, Liangcai Cao, and Guofan Jin. 2019. "Scaling of Three-Dimensional Computer-Generated Holograms with Layer-Based Shifted Fresnel Diffraction" Applied Sciences 9, no. 10: 2118. https://doi.org/10.3390/app9102118
APA StyleZhang, H., Cao, L., & Jin, G. (2019). Scaling of Three-Dimensional Computer-Generated Holograms with Layer-Based Shifted Fresnel Diffraction. Applied Sciences, 9(10), 2118. https://doi.org/10.3390/app9102118






