Mini-Review: Modeling and Performance Analysis of Nanocarbon Interconnects
Abstract
:1. Introduction
2. Graphene Nanoribbon (GNR) Interconnects
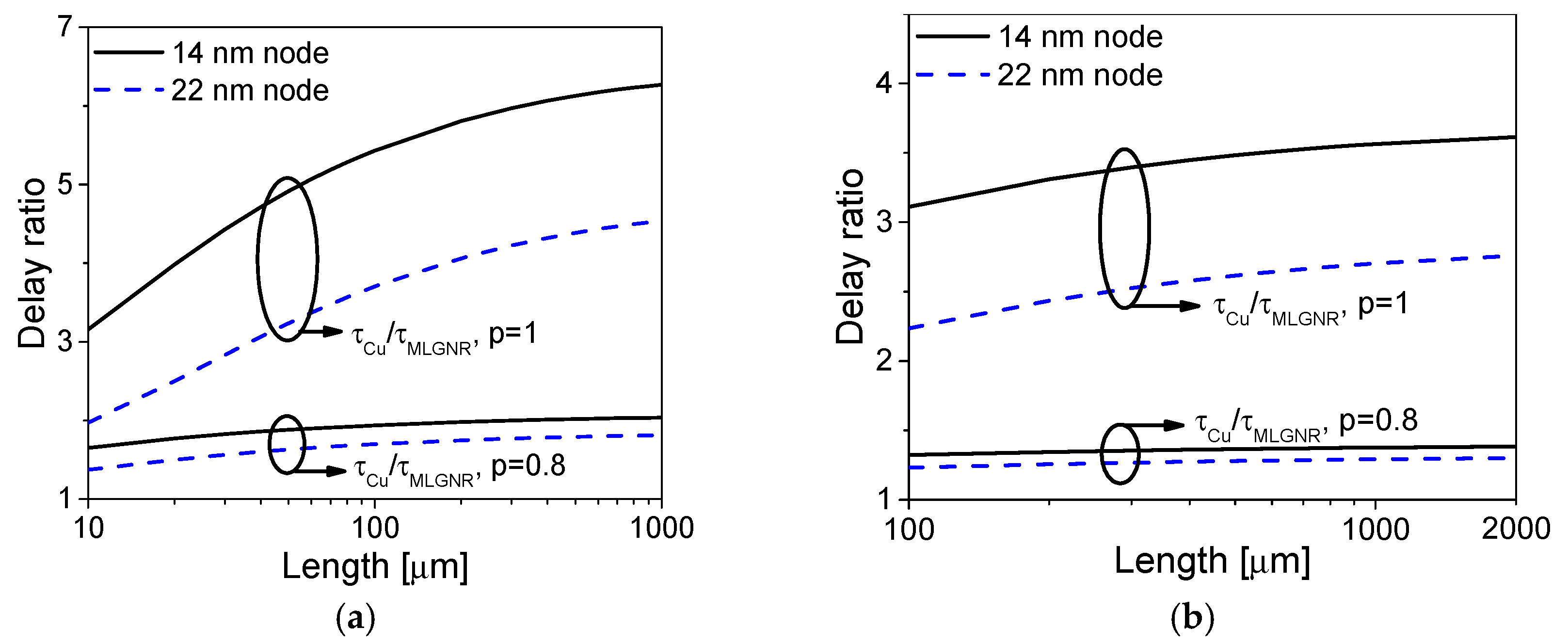
2.1. Multilayer Graphene Nanoribbon (MLGNR) Interconnects
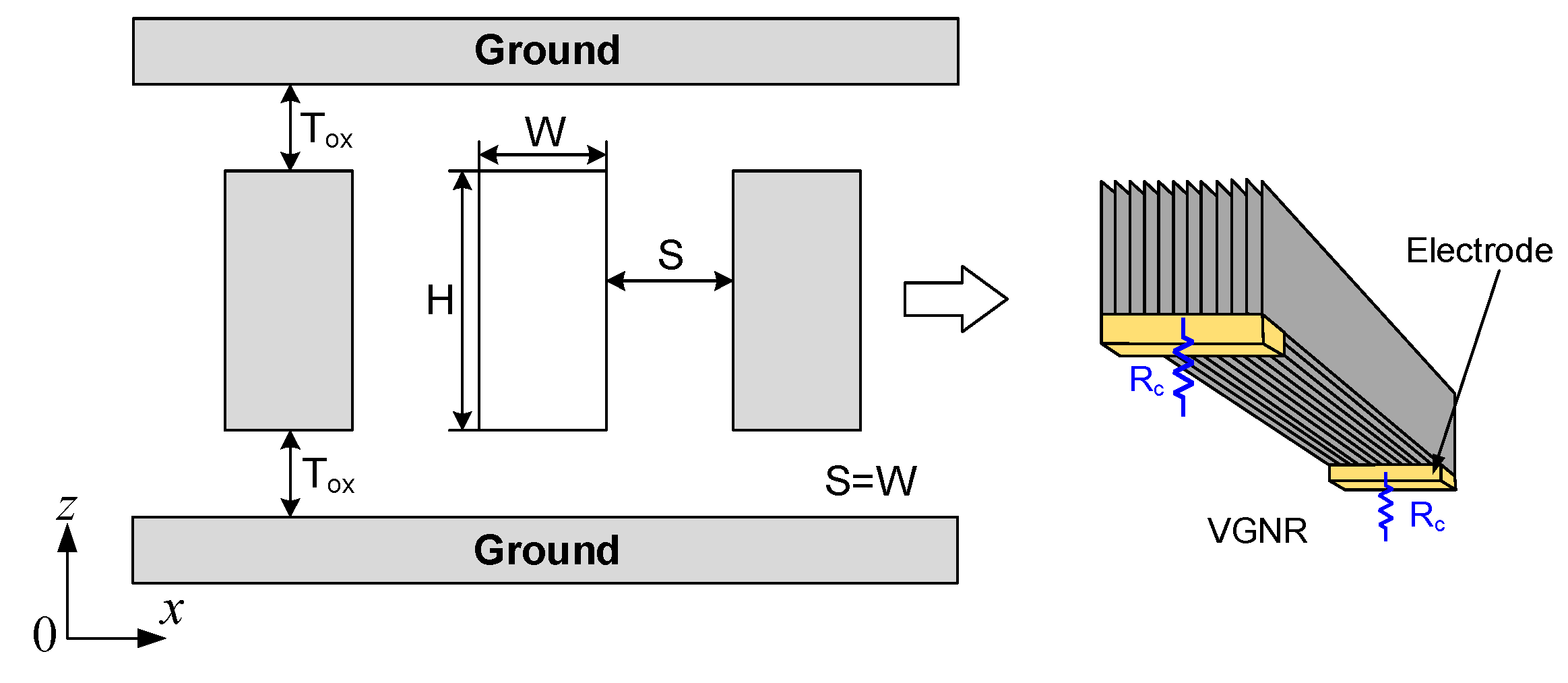
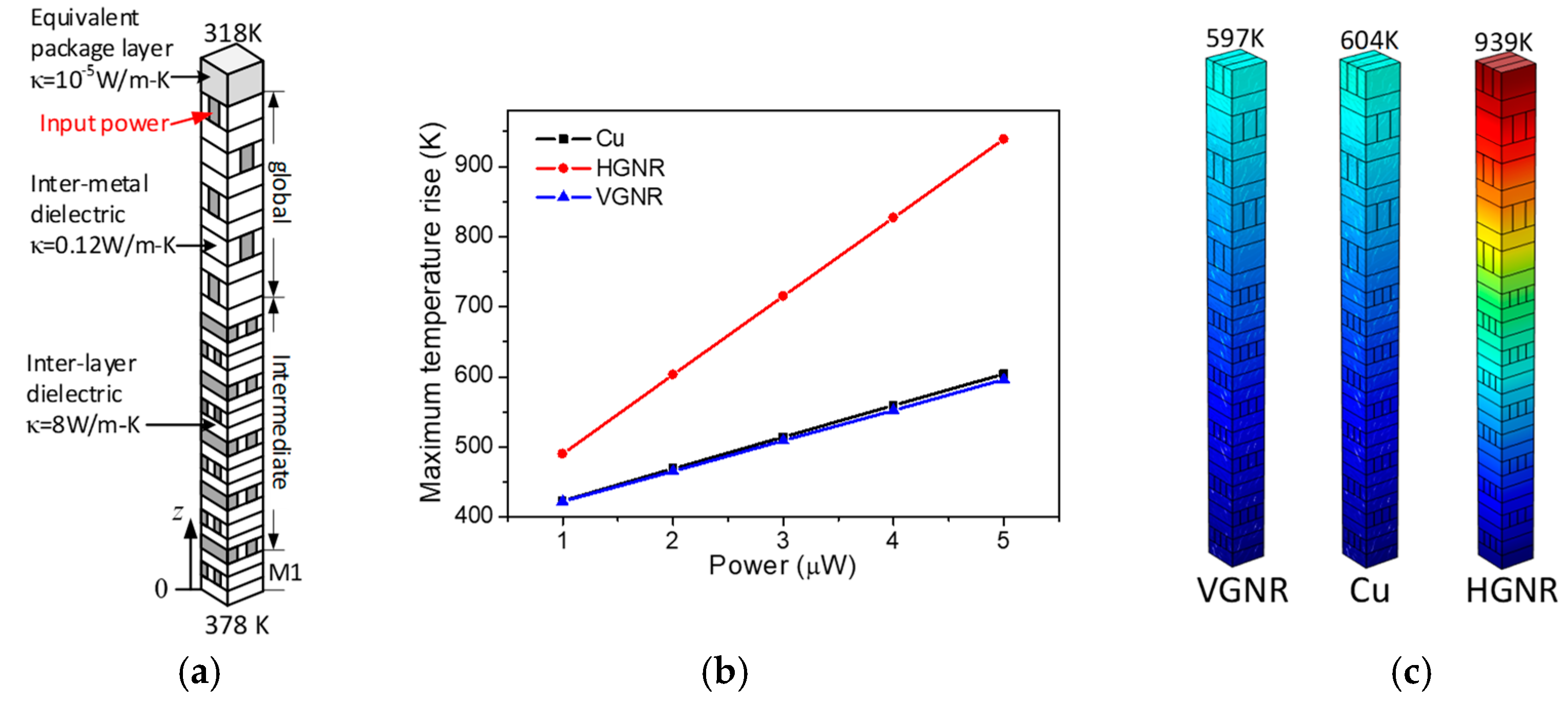
2.2. Vertical Graphene Nanoribbon (VGNR) Interconnects
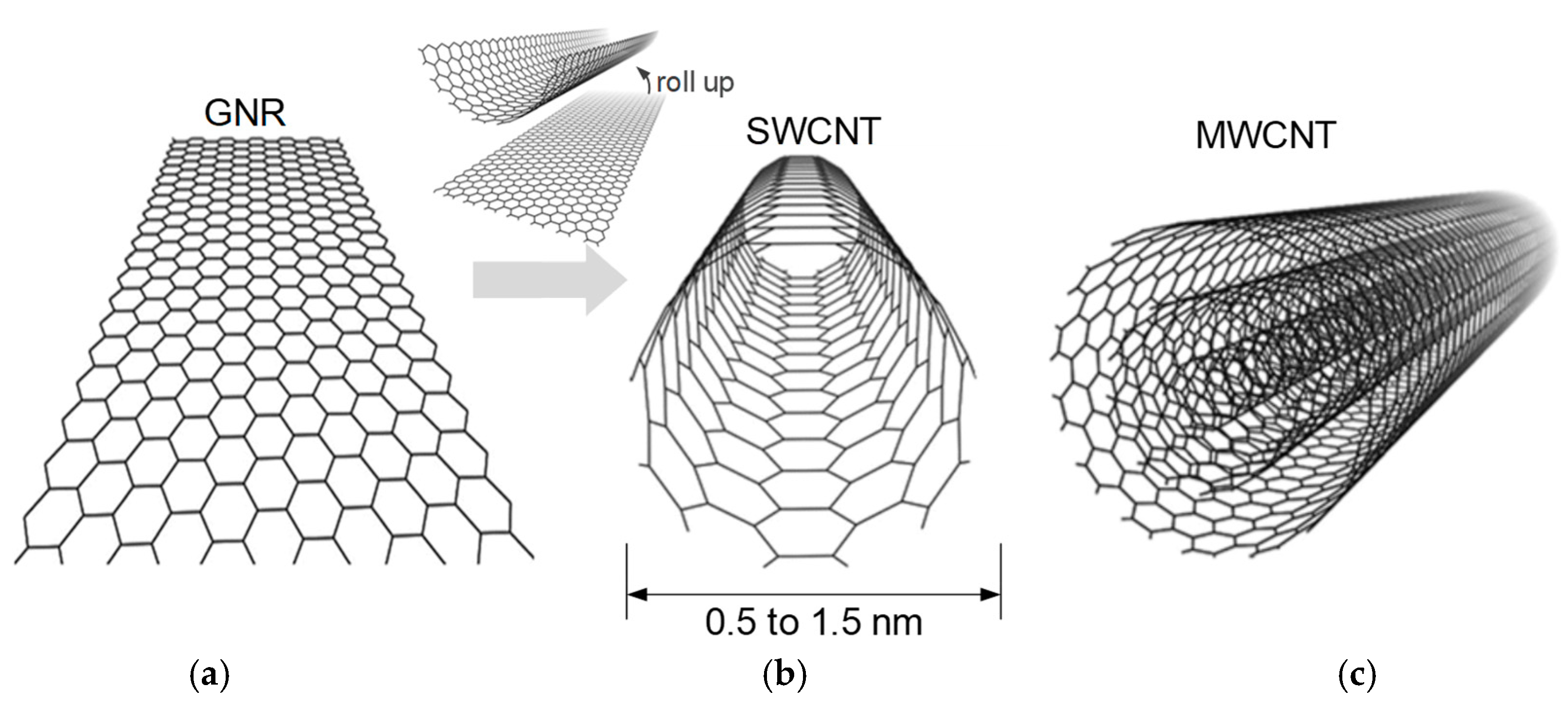
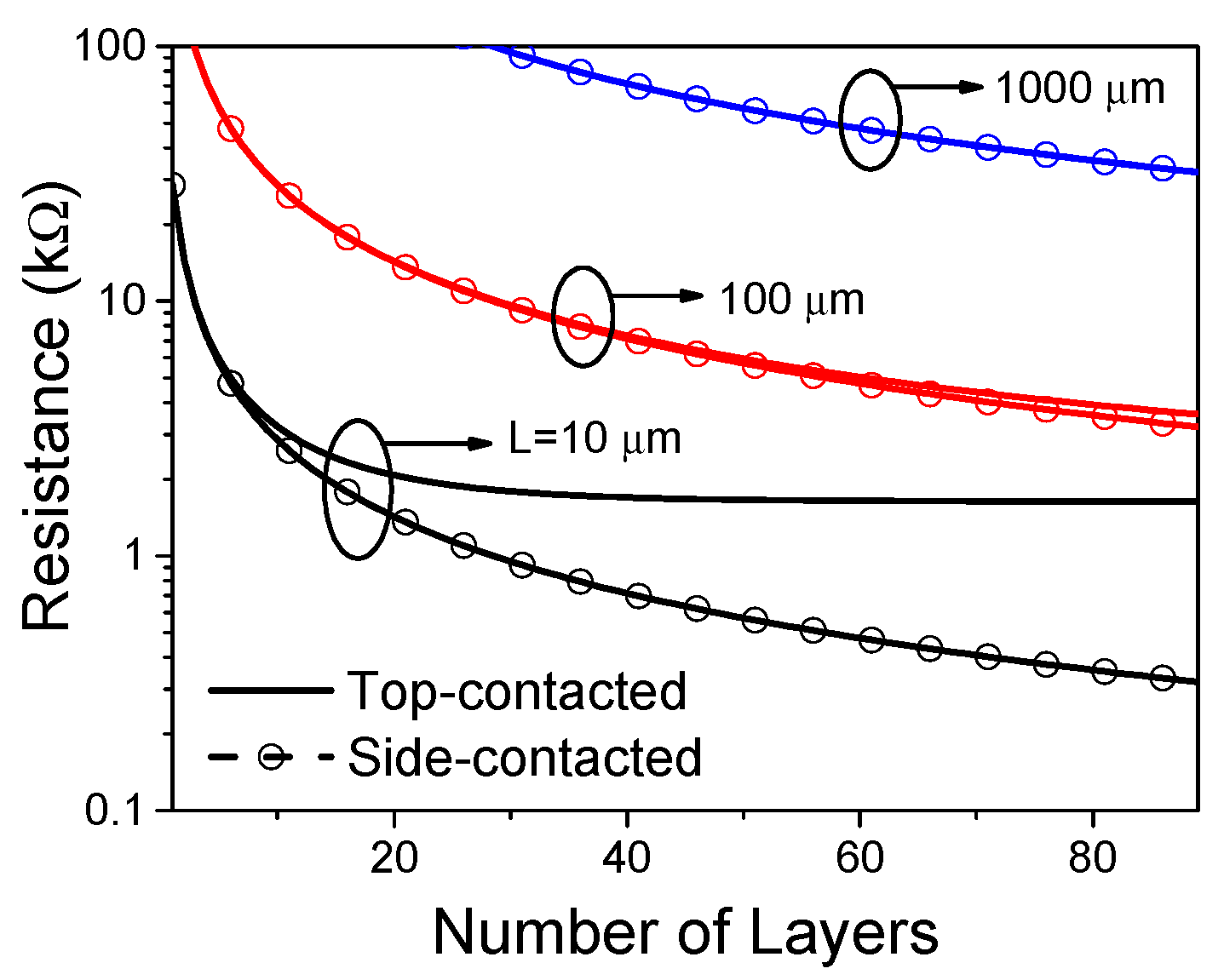
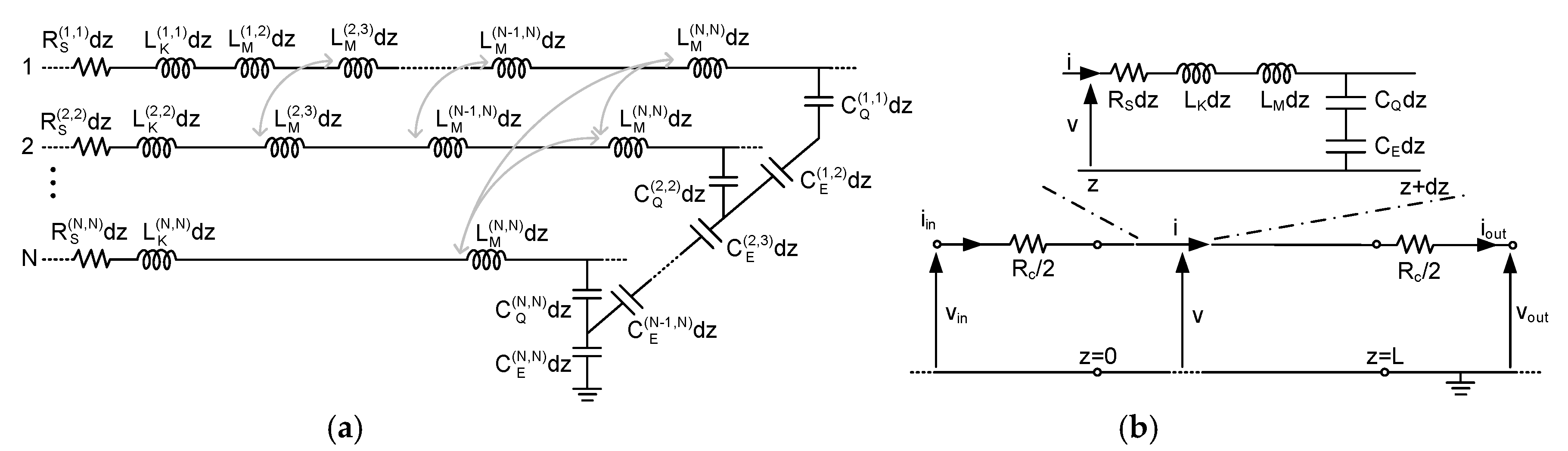
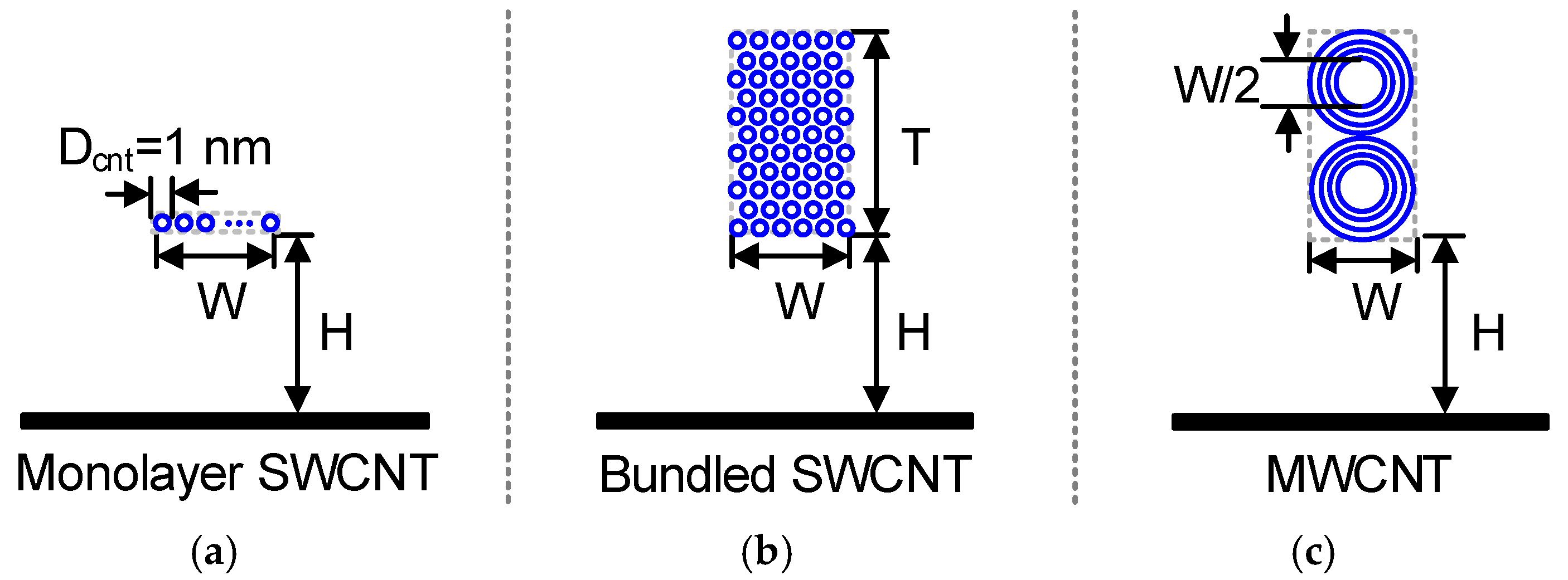
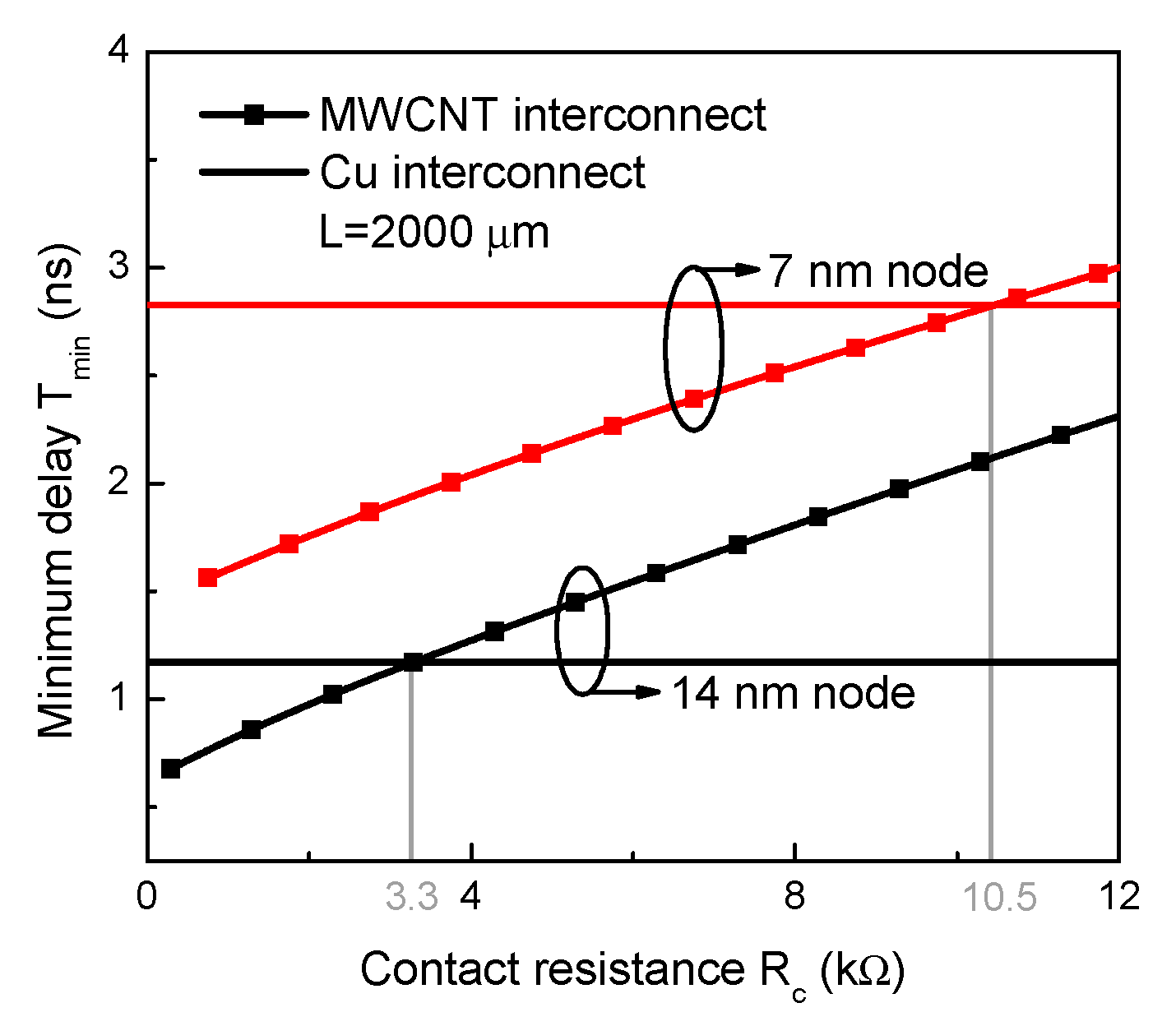
3. CNT Interconnects
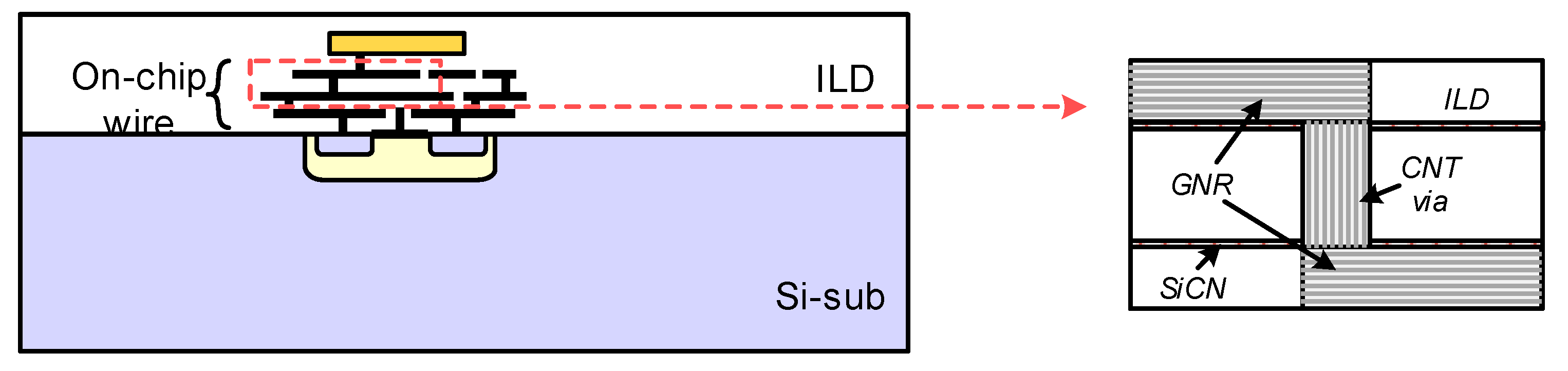
4. All-Carbon 3-D Interconnects
5. Cu-Nanocarbon Interconnect
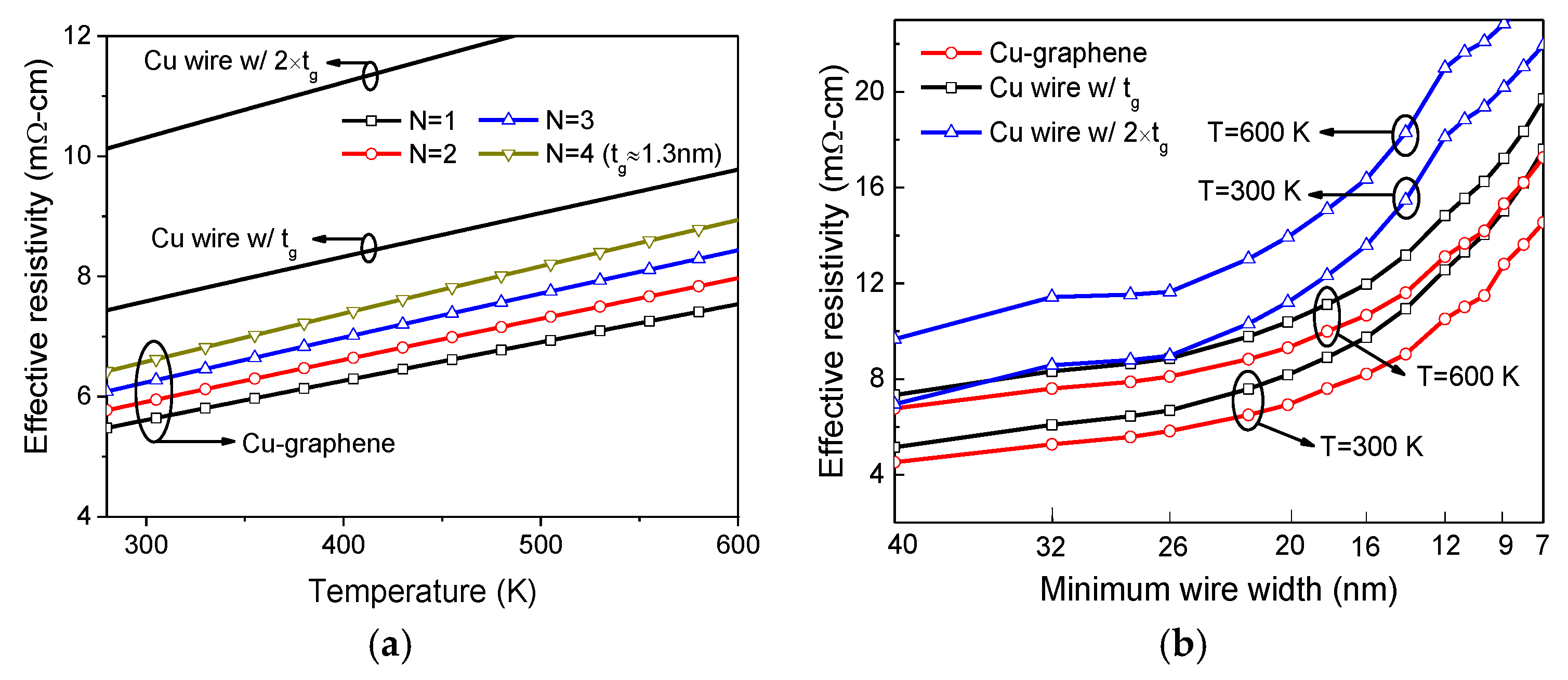
5.1. Cu-Graphene Interconnect
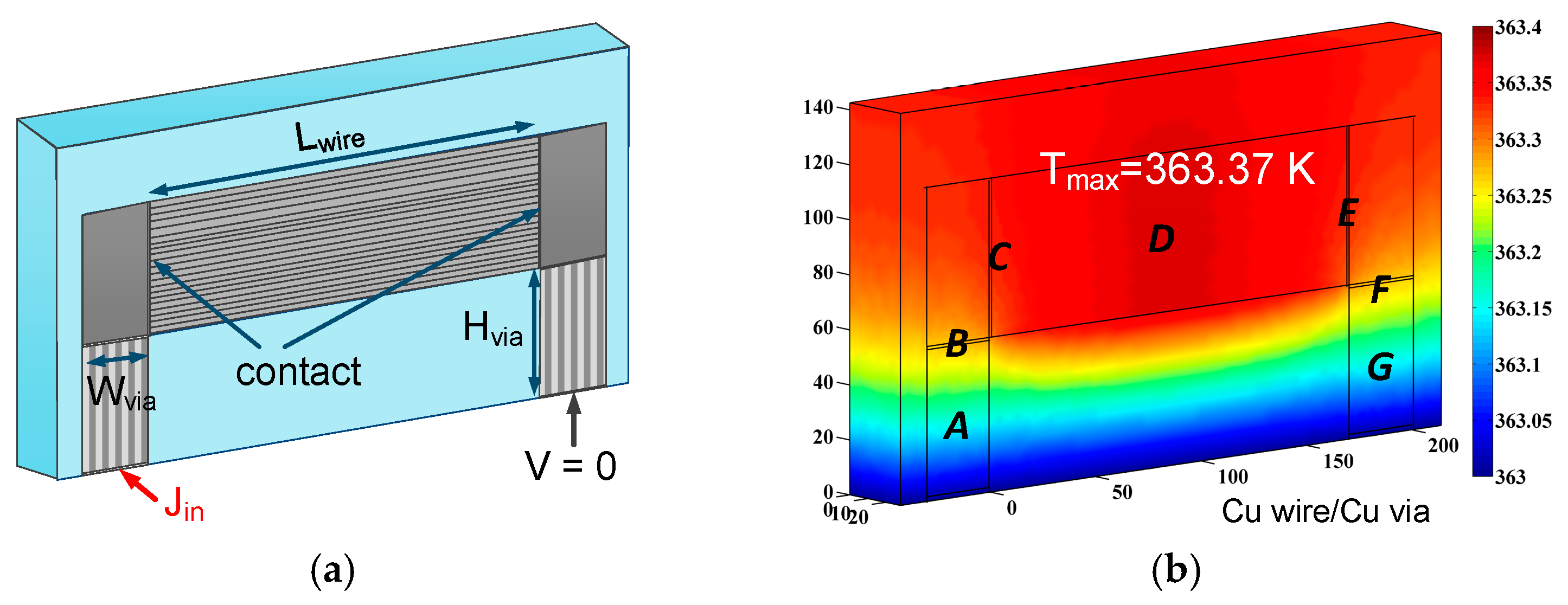
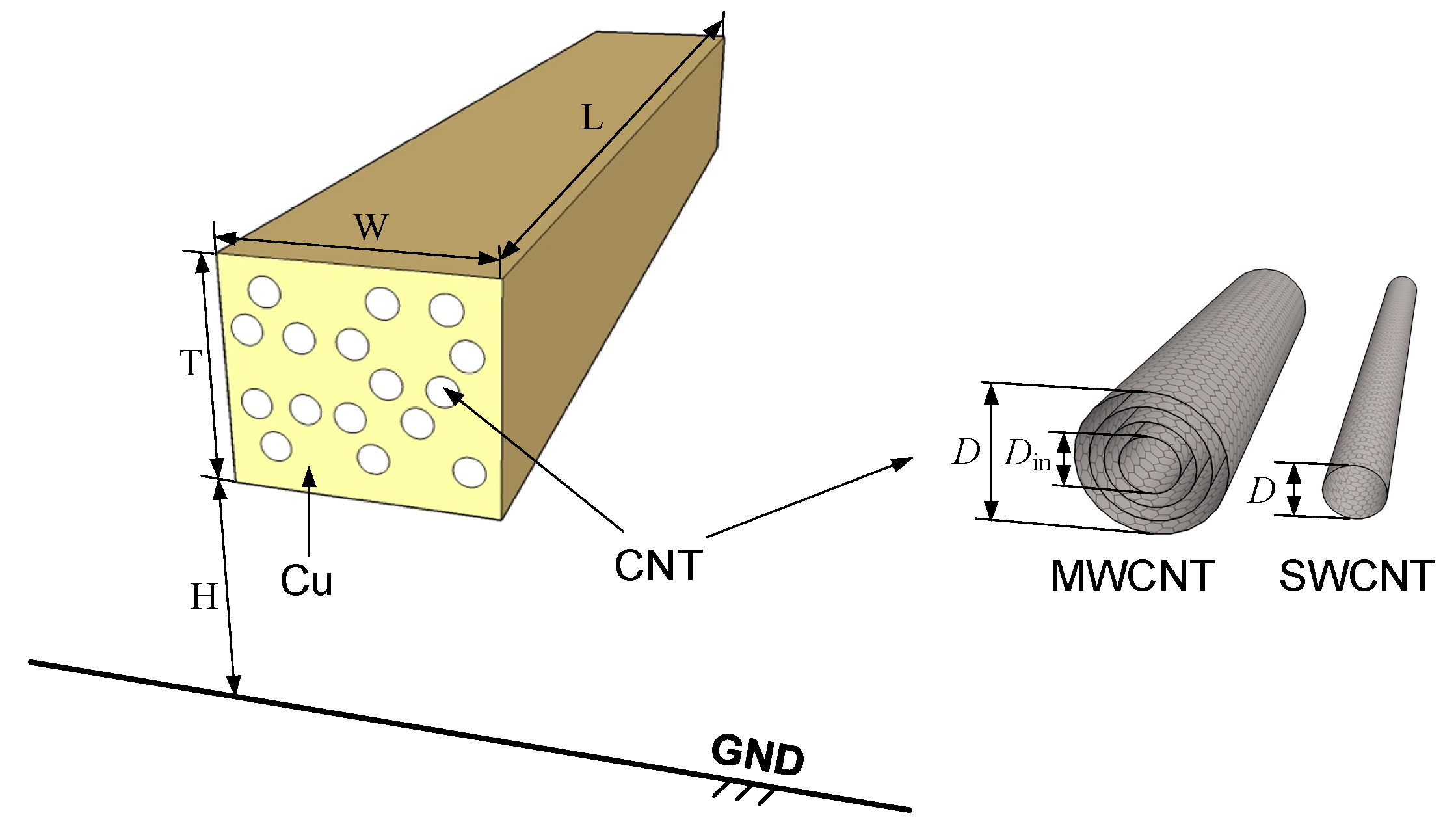
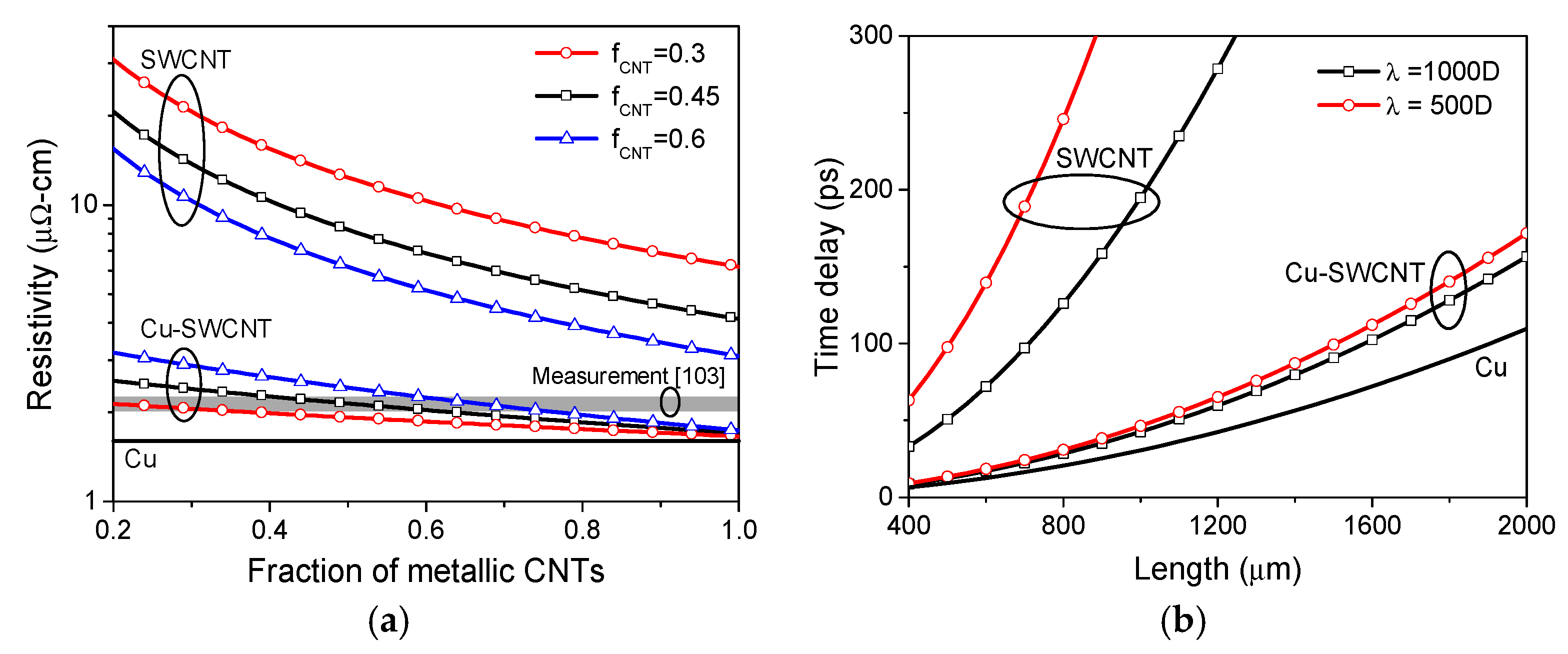
5.2. Cu-CNT Composite Interconnect
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moore, G.E. Cramming more components onto integrated circuits. Electronics 1965, 38, 114–117. [Google Scholar] [CrossRef]
- International Technology Roadmap for Semiconductors, Edition 2013. Available online: http://www.itrs2.net/ (accessed on 1 August 2017).
- Davis, J.A.; Venkatesan, R.; Kaloyeros, A.; Beylansky, M.; Souri, S.J.; Banerjee, K.; Saraswat, K.C.; Rahman, A.; Reif, R.; Meindl, J.D. Interconnect limits on gigascale integration (GSI) in the 21st century. Proc. IEEE 2001, 89, 305–324. [Google Scholar] [CrossRef]
- Banerjee, K.; Souri, S.J.; Kapur, P.; Saraswat, K.C. 3-D ICs: A novel chip design for improving deep-submicrometer interconnect performance and systems-on-chip integration. Proc. IEEE 2001, 89, 602–633. [Google Scholar] [CrossRef]
- Li, B.; Sullivan, T.D.; Lee, T.C.; Badami, D. Reliability challenges for copper interconnects. Microelectron. Reliab. 2004, 44, 365–380. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, K.; Metaev, E.; Pesic, M.; Lloyd, J.; Ring, M.; Paliwoda, P.; Tan, S.; Young, C.; Verzellsi, G.; et al. Reliability and modeling: What to simulate and how? In Proceedings of the INVITED IEEE International Integrated Reliability Workshop (IEEE IIRW), Fallen Leaf Lake, CA, USA, 8–12 October 2017. [Google Scholar]
- Meindl, J.D. Beyond Moore’s law: The interconnect era. Comput. Sci. Eng. 2003, 5, 20–24. [Google Scholar] [CrossRef]
- Ryan, J.G.; Geffken, R.M.; Poulin, N.R.; Paraszcazak, J.R. The evolution of interconnection technology at IBM. IBM J. Res. Dev. 1995, 39, 371–381. [Google Scholar] [CrossRef]
- Hayakawa, H.; Yoshikawa, N.; Yorozu, S.; Fujimaki, A. Superconducting digital electronics. Proc. IEEE 2004, 92, 1549–1563. [Google Scholar] [CrossRef]
- Sun, C.; Wade, M.T.; Lee, Y.; Orcutt, J.S.; Alloatti, L.; Georgas, M.S.; Waterman, A.S.; Shainline, J.M.; Avizienis, R.R.; Lin, S.; et al. Single-chip microprocessor than communicates directly using light. Nature 2015, 528, 534–538. [Google Scholar] [CrossRef] [PubMed]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Berber, S.; Kwon, Y.K.; Tomanek, D. Unusually high thermal conductivity of carbon nanotubes. Phys. Rev. Lett. 2000, 84, 4613. [Google Scholar] [CrossRef]
- Prasher, R. Graphene spreads the heat. Science 2010, 328, 185–186. [Google Scholar] [CrossRef]
- Wei, B.Q.; Vajtai, R.; Ajayan, P.M. Reliability and current carrying capacity of carbon nanotubes. Appl. Phys. Lett. 2001, 79, 1172–1174. [Google Scholar] [CrossRef]
- Pop, E.; Mann, D.; Reifenberg, J.; Goodson, K.; Dai, H. Electro-thermal transport in metallic single-wall carbon nanotubes for interconnect applications. IEDM Tech. Dig. 2005, 253–256. [Google Scholar]
- Li, H.; Xu, C.; Srivastava, N.; Banerjee, K. Carbon nanomaterials for next-generation interconnects and passives: Physics, status, and prospects. IEEE Trans. Electron. Devices 2009, 56, 1799–1821. [Google Scholar] [CrossRef]
- Maffucci, A. Carbon nanotubes in nanopackaging applications. IEEE Nanotechnol. Mag. 2009, 3, 22–25. [Google Scholar] [CrossRef]
- Chiariello, A.G.; Maffucci, A.; Miano, G. Circuit models of carbon-based interconnects for nanopackaging. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 1926–1937. [Google Scholar] [CrossRef]
- Maffucci, A.; Miano, G. Electrical properties of graphene for interconnect applications. Appl. Sci. 2014, 4, 305–317. [Google Scholar] [CrossRef]
- Zhao, W.S.; Yin, W.Y. Carbon-based interconnects for RF nanoelectronics. Wiley Encycl. Electr. Electron. Eng. 2012, 1–20. [Google Scholar] [CrossRef]
- Behnam, A.; Lyons, A.S.; Bae, M.H.; Chow, E.K.; Islam, S.; Neumann, C.M.; Pop, E. Transport in nanoribbon interconnects obtained from graphene grown by chemical vapor deposition. Nano Lett. 2012, 12, 4424–4430. [Google Scholar] [CrossRef]
- Kosynkin, D.V.; Higginbotham, A.L.; Sinitskii, A.; Lomeda, J.R.; Dimiev, A.; Price, B.K.; Tour, J.M. Longitudinal unzipping of carbon nanotubes to form graphene nanoribbon. Nature 2009, 458, 872–876. [Google Scholar] [CrossRef]
- Avouris, P. Graphene: Electronic and photonic properties and devices. Nano Lett. 2010, 10, 4285–4294. [Google Scholar] [CrossRef]
- Naeemi, A.; Meindl, J.D. Compact physics-based circuit models for graphene nanoribbon interconnects. IEEE Trans. Electron. Devices 2009, 56, 1822–1833. [Google Scholar] [CrossRef]
- Maffucci, A.; Miano, G. Number of conducting channels for armchair and zig-zag graphene nanoribbon interconnects. IEEE Trans. Nanotechnol. 2013, 12, 817–823. [Google Scholar] [CrossRef]
- Zhao, W.S.; Yin, W.Y. Comparative study on multilayer graphene nanoribbon (MLGNR) interconnects. IEEE Trans. Electromagn. Compat. 2014, 56, 638–645. [Google Scholar] [CrossRef]
- Rakheja, S.; Kumar, V.; Naeemi, A. Evaluation of the potential performance of graphene nanoribbons as on-chip interconnects. Proc. IEEE 2013, 101, 1740–1765. [Google Scholar] [CrossRef]
- Xu, C.; Li, H.; Banerjee, K. Modeling, analysis, and design of graphene nano-ribbon interconnects. IEEE Trans. Electron. Devices 2009, 56, 1567–1578. [Google Scholar] [CrossRef]
- Murali, R.; Yang, Y.; Brenner, K.; Beck, T.; Meindl, J.D. Breakdown current density of graphene nanoribbons. Appl. Phys. Lett. 2009, 94, 243114. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Kang, J.; Cao, W.; Xie, X.; Zhang, H.; Chu, J.H.; Liu, W.; Banerjee, K. Intercalation doped multilayer-graphene-nanoribbons for next-generation interconnects. Nano Lett. 2017, 17, 1482–1488. [Google Scholar] [CrossRef]
- Reina, A.; Jia, X.; Ho, J.; Nezich, D.; Son, H.; Bulovic, V.; Dresselhaus, M.S.; Kong, J. Large area, few-layer graphene films on arbitrary substrates by chemical vapor deposition. Nano Lett. 2008, 9, 30–35. [Google Scholar] [CrossRef]
- Faugeras, C.; Nerriere, A.; Potemski, M. Few-layer graphene on SiC, pyrolytic graphite, and graphene: A Raman scattering study. Appl. Phys. Lett. 2008, 92, 011914. [Google Scholar] [CrossRef]
- Sui, Y.; Appenzeller, J. Screening and interlayer coupling in multilayer graphene field effect transistors. Nano Lett. 2009, 9, 2973–2977. [Google Scholar] [CrossRef]
- Kumar, V.; Rakheja, S.; Naeemi, A. Performance and energy-per-bit modeling of multilayer graphene nanoribbon conductors. IEEE Trans. Electron. Devices 2012, 59, 2753–2761. [Google Scholar] [CrossRef]
- Pan, C.; Paghavan, P.; Ceyhan, A.; Catthoor, F.; Tokei, Z.; Naeemi, A. Technology/circuit/system co-optimization and benchmarking for multilayer graphene interconnects at sub-10 nm technology node. IEEE Trans. Electron. Devices 2015, 62, 1530–1536. [Google Scholar]
- Cui, J.P.; Zhao, W.S.; Yin, W.Y.; Hu, J. Signal transmission analysis of multilayer graphene nano-ribbon (MLGNR) interconnects. IEEE Trans. Electromagn. Compat. 2012, 54, 126–132. [Google Scholar] [CrossRef]
- Hass, J.; Varchon, F.; Millan-Otoya, J.E.; Sprinkle, M.; Sharma, N.; de Heer, W.A.; Berger, C.; First, P.N.; Magaud, L.; Conrad, E.H. Why multilayer graphene on 4H-SiC(0001) behaves like a single sheet of graphene. Phys. Rev. Lett. 2008, 100, 125504. [Google Scholar] [CrossRef]
- Sarto, M.S.; Tamburrano, A. Single-conductor transmission-line model of multiwall carbon nanotubes. IEEE Trans. Nanotechnol. 2010, 9, 82–92. [Google Scholar] [CrossRef]
- Kumar, V.R.; Majumder, M.K.; Kukkam, N.R.; Kaushik, B.K. Time and frequency domain analysis of MLGNR interconnects. IEEE Trans. Nanotechnol. 2015, 14, 484–492. [Google Scholar] [CrossRef]
- Ismail, Y.I.; Friedman, E.G. Effects of inductance on the propagation delay and repeater insertion in VLSI circuits. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2000, 8, 195–206. [Google Scholar] [CrossRef]
- Im, S.; Srivastava, N.; Banerjee, K.; Goodson, K.E. Scaling analysis of multilevel interconnect temperatures for high-performance ICs. IEEE Trans. Electron. Devices 2005, 52, 2710–2719. [Google Scholar] [CrossRef]
- Zhao, W.S.; Cheng, Z.H.; Wang, J.; Fu, K.; Wang, D.W.; Zhao, P.; Wang, G.; Dong, L. Vertical graphene nanoribbon interconnects at the end of the roadmap. IEEE Trans. Electron. Devices 2018, 65, 2632–2636. [Google Scholar] [CrossRef]
- Nihei, M.; Kawabata, A.; Murakami, T.; Sato, M.; Yokoyama, N. Improved thermal conductivity by vertical graphene contact formation for thermal TSVs. In Proceedings of the 2012 International Electron Devices Meeting, San Francisco, CA, USA, 10–13 December 2012; pp. 3351–3354. [Google Scholar]
- Wang, N.C.; Sinha, S.; Cline, B.; English, C.D.; Yeric, G.; Pop, E. Replacing copper interconnects with graphene at a 7-nm node. In Proceedings of the IEEE International Interconnect Technology Conference (IITC), Hsinchu, Taiwan, 16–18 May 2017; pp. 1–3. [Google Scholar]
- Wang, X.; Ouyang, Y.; Li, X.; Wang, H.; Guo, J.; Dia, H. Room-temperature all-semiconducting sub-10-nm graphene nanoribbon field-effect transistors. Phys. Rev. Lett. 2008, 100, 206803. [Google Scholar] [CrossRef]
- Pop, E.; Varshney, V.; Roy, V.K. Thermal properties of graphene: Fundamentals and applications. MRS Bull. 2012, 37, 1273–1281. [Google Scholar] [CrossRef] [Green Version]
- Shulaker, M.M.; Hills, G.; Park, R.S.; Howe, R.T.; Saraswat, K.; Wong, H.S.P.; Mitra, S. Three-dimensional integration of nanotechnologies for computing and data storage on a single chip. Nature 2017, 547, 74–78. [Google Scholar] [CrossRef]
- Li, F.; Cheng, H.M.; Bai, S.; Su, G.; Dresselhaus, M.S. Tensile strength of single-walled carbon nanotubes directly measured from their macroscopic ropes. Appl. Phys. Lett. 2000, 77, 3161–3163. [Google Scholar] [CrossRef]
- Li, H.J.; Lu, W.G.; Li, J.J.; Bai, X.D.; Gu, C.Z. Multichannel ballistic transport in multiwall carbon nanotubes. Phys. Rev. Lett. 2005, 95, 86601. [Google Scholar] [CrossRef]
- Maffucci, A.; Micciulla, F.; Cataldo, A.E.; Miano, G.; Bellucci, S. Modeling, fabrication, and characterization of large carbon nanotube interconnects with negative temperature coefficient of the resistance. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 485–493. [Google Scholar] [CrossRef]
- Burke, P.J. Luttinger liquid theory as a model of the gigahertz electrical properties of carbon nanotubes. IEEE Trans. Nanotechnol. 2002, 99, 129–144. [Google Scholar] [CrossRef]
- Liang, J.; Lee, J.; Berrada, S.; Georgiev, V.P.; Pandey, R.; Chen, R.; Asenov, A.; Todri-Sanial, A. Atomistic- to circuit-level modeling of doped SWCNT for on-chip interconnects. IEEE Trans. Nanotechnol. 2018, 17, 1084–1088. [Google Scholar] [CrossRef]
- Miano, G.; Forestiere, C.; Maffucci, A.; Maksimenko, S.A.; Slepyan, G.Y. Signal propagation in carbon nanotubes of arbitrary chirality. IEEE Trans. Nanotechnol. 2011, 10, 135–149. [Google Scholar] [CrossRef]
- Jamal, O.; Naeemi, A. Ultralow-power single-wall carbon nanotube interconnects for subthreshold circuits. IEEE Trans. Nanotechnol. 2011, 10, 99–101. [Google Scholar] [CrossRef]
- Pable, S.D.; Hasan, M. Interconnect design for subthreshold circuits. IEEE Trans. Nanotechnol. 2012, 11, 633–639. [Google Scholar] [CrossRef]
- Ceyhan, A.; Naeemi, A. Cu interconnect limitations and opportunities for SWNT interconnects at the end of the roadmap. IEEE Trans. Electron. Devices 2013, 60, 374–382. [Google Scholar] [CrossRef]
- Naeemi, A.; Meindl, J.D. Monolayer metallic nanotube interconnects: Promising candidates for short local interconnects. IEEE Electron. Device Lett. 2005, 26, 544–546. [Google Scholar] [CrossRef]
- Zhao, W.S.; Wang, G.; Hu, J.; Sun, L.; Hong, H. Performance and stability analysis of monolayer single-walled carbon nanotube interconnects. Int. J. Numer. Modell. Electron. Netw. Devices Fields 2015, 28, 456–464. [Google Scholar] [CrossRef]
- Li, H.; Liu, W.; Cassell, A.M.; Kreupl, F.; Banerjee, K. Low-resistivity long-length horizontal carbon nanotube bundles for interconnect applications—Part I: Process development. IEEE Trans. Electron. Devices 2013, 60, 2862–2869. [Google Scholar] [CrossRef]
- Majumder, M.K.; Pandya, N.D.; Kaushik, B.K.; Manhas, S.K. Analysis of MWCNT and bundled SWCNT interconnects: Impact on crosstalk and area. IEEE Electron. Device Lett. 2012, 33, 1180–1182. [Google Scholar] [CrossRef]
- Majumder, M.K.; Kaushik, B.K.; Manhas, S.K. Analysis of delay and dynamic crosstalk in bundled carbon nanotube interconnects. IEEE Trans. Electromagn. Compat. 2014, 56, 1666–1673. [Google Scholar] [CrossRef]
- Harutyunyan, A.R.; Chen, G.; Paronyan, T.M.; Pigos, E.M.; Kuznetsov, O.A.; Hewaparakrama, K.; Kim, S.M.; Zakharov, D.; Stach, E.A.; Sumanasekera, G.U. Preferential growth of single-walled carbon nanotubes with metallic conductivity. Science 2009, 326, 116–120. [Google Scholar] [CrossRef]
- Naeemi, A.; Meindl, J.D. Design and performance modeling for single-walled carbon nanotubes as local, semiglobal, and global interconnects in gigascale integrated systems. IEEE Trans. Electron. Devices 2007, 54, 26–37. [Google Scholar] [CrossRef]
- Awano, Y.; Sato, S.; Nihei, M.; Sakai, T.; Ohno, Y.; Mizutani, T. Carbon nanotubes for VLSI: Interconnect and transistor applications. Proc. IEEE 2010, 98, 2015–2030. [Google Scholar] [CrossRef]
- Srivastava, N.; Li, H.; Kreupl, F.; Banerjee, K. On the applicability of single-walled carbon nanotubes as VLSI interconnects. IEEE Trans. Nanotechnol. 2009, 8, 542–559. [Google Scholar] [CrossRef]
- Chiariello, A.G.; Maffucci, A.; Miano, G. Electrical modeling of carbon nanotube vias. IEEE Trans. Electromagn. Compat. 2012, 54, 158–166. [Google Scholar] [CrossRef]
- Li, H.; Srivastava, N.; Mao, J.F.; Yin, W.Y.; Banerjee, K. Carbon nanotube vias: Does Ballistic electron-phonon transport imply improved performance and reliability? IEEE Trans. Electron. Devices 2011, 58, 2689–2701. [Google Scholar] [CrossRef]
- Naeemi, A.; Meindl, J.D. Physical modeling of temperature coefficient of resistance for single- and multi-wall carbon nanotube interconnects. IEEE Electron. Device Lett. 2007, 28, 135–138. [Google Scholar] [CrossRef]
- Li, H.; Yin, W.Y.; Banerjee, K.; Mao, J.F. Circuit modeling and performance analysis of multi-walled carbon nanotube interconnects. IEEE Trans. Electron. Devices 2008, 55, 1328–1337. [Google Scholar] [CrossRef]
- Tang, M.; Mao, J. Modeling and fast simulation of multiwalled carbon nanotube interconnects. IEEE Trans. Electromagn. Compat. 2015, 57, 232–240. [Google Scholar] [CrossRef]
- Liang, F.; Wang, G.; Ding, W. Estimation of time delay and repeater insertion in multiwall carbon nanotube interconnects. IEEE Trans. Electron. Devices 2011, 58, 2712–2720. [Google Scholar] [CrossRef]
- Pu, S.N.; Yin, W.Y.; Mao, J.F.; Liu, Q.H. Crosstalk prediction of single- and double-walled carbon-nanotube (SWCNT/DWCNT) bundle interconnects. IEEE Trans. Electron. Devices 2009, 56, 560–568. [Google Scholar] [CrossRef]
- Liang, F.; Wang, G.; Lin, H. Modeling of crosstalk effects in multiwall carbon nanotube interconnects. IEEE Trans. Electromagn. Compat. 2011, 54, 133–139. [Google Scholar] [CrossRef]
- Kumar, M.G.; Chandel, R.; Agrawal, Y. An efficient crosstalk model for coupled multiwalled carbon nanotube interconnects. IEEE Trans. Electromagn. Compat. 2018, 60, 487–496. [Google Scholar] [CrossRef]
- Chen, R.; Liang, J.; Lee, J.; Georgiev, V.P.; Ramos, R.; Okuno, H.; Kalita, D.; Cheng, Y.; Zhang, L.; Pandey, R.R.; et al. Variability study of MWCNT local interconnects considering defects and contact resistances—Part I: Pristine MWCNT. IEEE Trans. Electron. Devices 2018, 65, 4955–4962. [Google Scholar] [CrossRef]
- Chen, R.; Liang, J.; Lee, J.; Georgiev, V.P.; Ramos, R.; Okuno, H.; Kalita, D.; Cheng, Y.; Zhang, L.; Pandey, R.R.; et al. Variability study of MWCNT local interconnects considering defects and contact resistances—Part II: Impact of charge transfer doping. IEEE Trans. Electron. Devices 2018, 65, 4963–4970. [Google Scholar] [CrossRef]
- Chen, W.C.; Yin, W.Y.; Jia, L.; Liu, Q.H. Electrothermal characterization of single-walled carbon nanotube (SWCNT) interconnect arrays. IEEE Trans. Nanotechnol. 2009, 8, 718–728. [Google Scholar] [CrossRef]
- Verma, R.; Bhattacharya, S.; Mahapatra, S. Analytical solution of Joule-heating equation for metallic single-walled carbon nanotube interconnects. IEEE Trans. Electron. Devices 2011, 58, 3991–3996. [Google Scholar] [CrossRef]
- Mohsin, K.M.; Srivastava, A. Modeling of Joule heating induced effects in multiwall carbon nanotube interconnects. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 3089–3098. [Google Scholar] [CrossRef]
- Mishra, A.; Shrivastava, M. ESD behavior of MWCNT interconnects–Part I: Observations and insights. IEEE Trans. Device Mater. Reliab. 2017, 17, 600–607. [Google Scholar] [CrossRef]
- Mishra, A.; Shrivastava, M. ESD behavior of MWCNT interconnects—Part II: Unique current conduction mechanism. IEEE Trans. Device Mater. Reliab. 2017, 17, 608–615. [Google Scholar] [CrossRef]
- Guistininai, A.; Tucci, V.; Zamboni, W. Modeling issues and performance analysis of high-speed interconnects based on a bundle of SWCNT. IEEE Trans. Electron. Devices 2010, 57, 1978–1986. [Google Scholar] [CrossRef]
- Matsuda, Y.; Deng, W.Q.; Goddard, W.A., III. Contact resistance for “end-contacted” metal-graphene and metal-nanotube interfaces from quantum mechanics. J. Phys. Chem. C 2010, 114, 17845–17850. [Google Scholar] [CrossRef]
- Zhao, W.S.; Wang, G.; Sun, L.; Yin, W.Y.; Guo, Y.X. Repeater insertion for carbon nanotube interconnects. Micro Nano Lett. 2014, 9, 337–339. [Google Scholar] [CrossRef]
- Liu, P.W.; Cheng, Z.H.; Zhao, W.S.; Lu, Q.; Zhu, Z.; Wang, G. Repeater insertion for multi-walled carbon nanotube interconnects. Appl. Sci. 2018, 8, 236. [Google Scholar] [CrossRef]
- Banerjee, K.; Mehrotra, A. A power-optimal repeater insertion methodology for global interconnects in nanometer design. IEEE Trans. Electron. Devices 2002, 49, 2001–2007. [Google Scholar] [CrossRef]
- Chen, G.; Friedman, E.G. Low-power repeaters driving RC and RLC interconnects with delay and bandwidth constraints. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2006, 14, 161–172. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.S.; Liu, P.W.; Yu, H.; Hu, Y.; Wang, G.; Swaminathan, M. Repeater insertion to reduce delay and power in copper and carbon nanotube-based nanointerconnects. IEEE Access 2019, 7, 13622–13633. [Google Scholar] [CrossRef]
- Nihei, M.; Kawabata, A.; Murakami, T.; Sato, M.; Yokoyama, N. CNT/graphene technologies for future carbon-based interconnects. In Proceedings of the IEEE 11th International Conference on Solid-State and Integrated Circuit Technology, Xi’an, China, 29 October–1 November 2012; pp. 1–4. [Google Scholar]
- Ramos, R.; Fournier, A.; Fayolle, M.; Dijon, J.; Murray, C.P.; McKenna, J. Nanocarbon interconnects combining vertical CNT interconnects and horizontal graphene lines. In Proceedings of the 2016 IEEE International Interconnect Technology Conference/Advanced Metallization Conference (IITC/AMC), San Jose, CA, USA, 23–26 May 2016; pp. 48–50. [Google Scholar]
- Zhou, C.; Senegor, R.; Baron, Z.; Chen, Y.; Raju, S.; Vyas, A.A.; Chan, M.; Chai, Y.; Yang, C.Y. Synthesis and interface characterization of CNTs on graphene. Nanotechnology 2017, 28, 054007. [Google Scholar] [CrossRef]
- Jiang, J.; Kang, J.; Chu, J.H.; Banerjee, K. All-carbon interconnect scheme integrating graphene-wires and carbon-nanotube-vias. IEDM Tech. Dig. 2017, 1431–1434. [Google Scholar]
- Li, N.; Mao, J.; Zhao, W.S.; Tang, M.; Chen, W.; Yin, W.Y. Electrothermal cosimulation of 3-D carbon-based heterogeneous interconnects. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 518–526. [Google Scholar] [CrossRef]
- Zhang, G.; Warner, J.H.; Fouque, M.; Robertson, A.W.; Chen, B.; Robertson, J. Growth of ultrahigh density single-walled carbon nanotube forests by improved catalyst design. ACS Nano 2012, 6, 2893–2903. [Google Scholar] [CrossRef]
- Eda, G.; Fanchini, G.; Chhowalla, M. Large-area ultrathin films of reduced graphene oxide as a transparent and flexible electronic material. Nat. Nanotechnol. 2008, 3, 270–274. [Google Scholar] [CrossRef]
- Ceyhan, A.; Naeemi, A. Cu/low-k interconnect technology design and benchmarking for future technology nodes. IEEE Trans. Electron. Devices 2013, 60, 4041–4047. [Google Scholar] [CrossRef]
- Nguyen, B.S.; Lin, J.F.; Perng, D.C. 1-nm-thick graphene tri-layer as the ultimate copper diffusion barrier. Appl. Phys. Lett. 2014, 104, 082105. [Google Scholar] [CrossRef]
- Hong, J.; Lee, S.; Lee, S.; Han, H.; Mahata, C.; Yeon, H.W.; Koo, B.; Kim, S.I.; Nam, T.; Byun, K.; et al. Graphene as an atomically thin barrier to Cu diffusion into Si. Nanoscale 2014, 6, 7503–7511. [Google Scholar] [CrossRef]
- Li, L.; Chen, X.; Wang, C.H.; Cao, J.; Lee, S.; Tang, A.; Ahn, C.; Roy, S.S.; Arnold, M.S.; Wong, H.S.P. Vertical and lateral copper transport through graphene layers. ACS Nano 2015, 9, 8361–8367. [Google Scholar] [CrossRef] [PubMed]
- Kang, C.G.; Lim, S.K.; Lee, S.; Lee, S.K.; Cho, C.; Lee, Y.G.; Hwang, H.J.; Kim, Y.; Choi, H.J.; Choe, S.H. Effects of multi-layer graphene capping on Cu interconnects. Nanotechnology 2013, 24, 115707. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, R.; Zhao, W.S.; Hu, J.; Yin, W.Y. Electrothermal characterization of multilevel Cu-graphene heterogenesou interconnects in the presence of an electrostatic discharge (ESD). IEEE Trans. Nanotechnol. 2015, 14, 205–209. [Google Scholar] [CrossRef]
- Mehta, R.; Chugh, S.; Chen, Z. Enhanced electrical and thermal conduction in graphene-encapsulated copper nanowires. Nano Lett. 2015, 15, 2024–2030. [Google Scholar] [CrossRef] [PubMed]
- Goli, P.; Ning, H.; Li, X.; Liu, C.Y.; Novoselov, K.S.; Balandin, A.A. Thermal properties of graphene-copper-graphene heterogeneous films. Nano Lett. 2014, 14, 1497–1503. [Google Scholar] [CrossRef]
- Li, L.; Zhu, Z.; Yoon, A.; Wong, H.S.P. In-situ grown graphene enables copper interconnects with improved eletromigration reliability. IEEE Electron. Device Lett. 2019. [Google Scholar] [CrossRef]
- Mehta, R.; Chugh, S.; Chen, Z. Transfer-free multi-layer graphene as a diffusion barrier. Nanoscale 2017, 9, 1827–1833. [Google Scholar] [CrossRef]
- Li, C.L.; Zhang, S.; Shen, T.; Appenzeller, J.; Chen, Z. BEOL compatible 2D layered materials as ultra-thin diffusion barriers for Cu interconnect technology. In Proceedings of the IEEE 75th Annual Device Research Conference (DRC), South Bend, IN, USA, 25–28 June 2017; pp. 1–2. [Google Scholar]
- Zhao, W.S.; Wang, D.W.; Wang, G.; Yin, W.Y. Electrical modeling of on-chip Cu-graphene heterogeneous interconnects. IEEE Electron. Device Lett. 2015, 36, 74–76. [Google Scholar] [CrossRef]
- Cheng, Z.H.; Zhao, W.S.; Wang, D.W.; Wang, J.; Dong, L.; Wang, G.; Yin, W.Y. Analysis of Cu-graphene interconnects. IEEE Access 2018, 6, 53499–53508. [Google Scholar] [CrossRef]
- Subramaniam, C.; Yamada, T.; Kobashi, K.; Sekiguchi, A.; Futaba, D.N.; Yumura, M.; Hata, K. One hundred fold increase in current carrying capacity in a carbon nanotube-copper composite. Nat. Commun. 2013, 4, 2202. [Google Scholar] [CrossRef]
- Chai, Y.; Chan, P.C.H.; Fu, Y.; Chuang, Y.C.; Liu, C.Y. Electromigraiton studies of Cu/carbon nanotube composite interconnects using Blech structure. IEEE Electron. Device Lett. 2008, 29, 1001–1003. [Google Scholar] [CrossRef]
- Lee, J.; Berrada, S.; Adamu-Lema, F.; Nagy, N.; Georgiev, V.P.; Sadi, T.; Liang, J.; Ramos, R.; Carrillo-Nunez, H.; Kalita, D.; et al. Understanding electromigration in Cu-CNT composite interconnects: A multiscale electrothermal simulation study. IEEE Trans. Electron. Devices 2018, 65, 3884–3892. [Google Scholar] [CrossRef]
- Cheng, Z.H.; Zhao, W.S.; Dong, L.; Wang, J.; Zhao, P.; Gao, H.; Wang, G. Investigation of copper-carbon nanotube composites as global VLSI interconnects. IEEE Trans. Nanotechnol. 2017, 16, 891–900. [Google Scholar] [CrossRef]
- Zhao, W.S.; Zheng, J.; Hu, Y.; Sun, S.; Wang, G.; Dong, L.; Yu, L.; Sun, L.; Yin, W.Y. High-frequency analysis of Cu-carbon nanotube composite through-silicon vias. IEEE Trans. Nanotechnol. 2016, 15, 506–511. [Google Scholar] [CrossRef]
- Xu, C.; Li, H.; Suaya, R.; Banerjee, K. Compact AC modeling and performance analysis of through-silicon vias in 3-D ICs. IEEE Trans. Electron. Devices 2010, 57, 3405–3417. [Google Scholar] [CrossRef]







| Solution | Pros | Cons |
|---|---|---|
| Cu [2,4] |
|
|
| MLGNR [23,26,29,31,44,85] |
|
|
| VGNR [13,23,29,31,44,45] |
|
|
| Bundled SWCNTs [16,17,44,61,64,96] |
|
|
| MWCNT [44,51,62,82,85] |
|
|
| Cu-graphene [2,104,105,108,110] |
|
|
| Cu-CNT composite [2,4,111,112] |
|
|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.-S.; Fu, K.; Wang, D.-W.; Li, M.; Wang, G.; Yin, W.-Y. Mini-Review: Modeling and Performance Analysis of Nanocarbon Interconnects. Appl. Sci. 2019, 9, 2174. https://doi.org/10.3390/app9112174
Zhao W-S, Fu K, Wang D-W, Li M, Wang G, Yin W-Y. Mini-Review: Modeling and Performance Analysis of Nanocarbon Interconnects. Applied Sciences. 2019; 9(11):2174. https://doi.org/10.3390/app9112174
Chicago/Turabian StyleZhao, Wen-Sheng, Kai Fu, Da-Wei Wang, Meng Li, Gaofeng Wang, and Wen-Yan Yin. 2019. "Mini-Review: Modeling and Performance Analysis of Nanocarbon Interconnects" Applied Sciences 9, no. 11: 2174. https://doi.org/10.3390/app9112174
APA StyleZhao, W.-S., Fu, K., Wang, D.-W., Li, M., Wang, G., & Yin, W.-Y. (2019). Mini-Review: Modeling and Performance Analysis of Nanocarbon Interconnects. Applied Sciences, 9(11), 2174. https://doi.org/10.3390/app9112174






