Stability of Reinforced Retaining Wall under Seismic Loads
Abstract
:1. Introduction
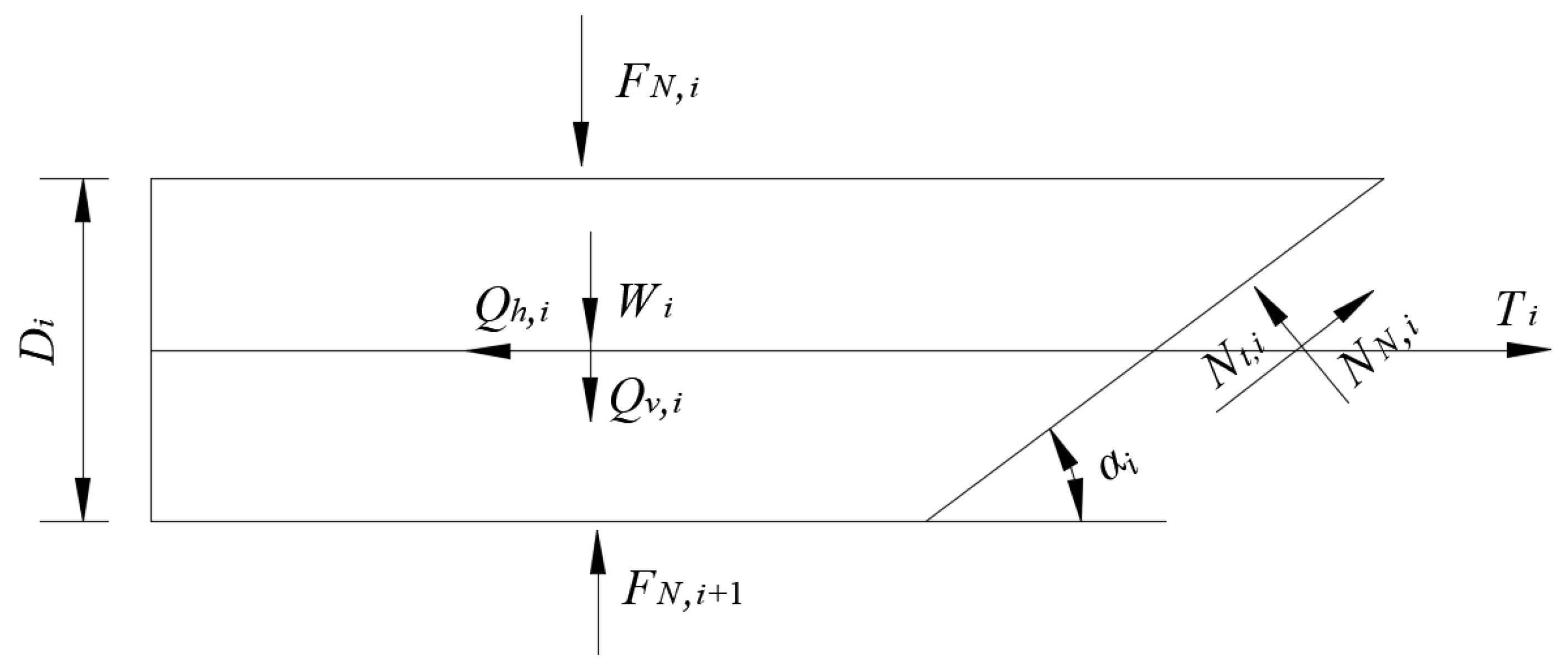
2. Assumptions and Formulation of the Horizontal Slice Method (HSM)
2.1. Basic Assumptions of HSM
- (1)
- The log spiral slip surface line of the reinforced retaining wall passes through the toe of the wall.
- (2)
- The sliding body of the retaining wall is divided into several horizontal slices, the number of which is equal to that of reinforcement layers, and each slice contains reinforcement [32].
- (3)
- The horizontal shear force between reinforcements is ignored.
- (4)
- The safety factor is assumed to be equal for various slices [23].
- (5)
- Both horizontal and vertical seismic actions are applied to the center of gravity of the slice.
- (6)
- The analysis is done by the limited equilibrium method.
- (7)
- The anchoring strength of the reinforcement and the resistance of the reinforcement against pulling out are not taken into account.
2.2. Formulation of the HSM
3. Seismic Loads
4. Tensile Force of Reinforcement
5. Parametric Study
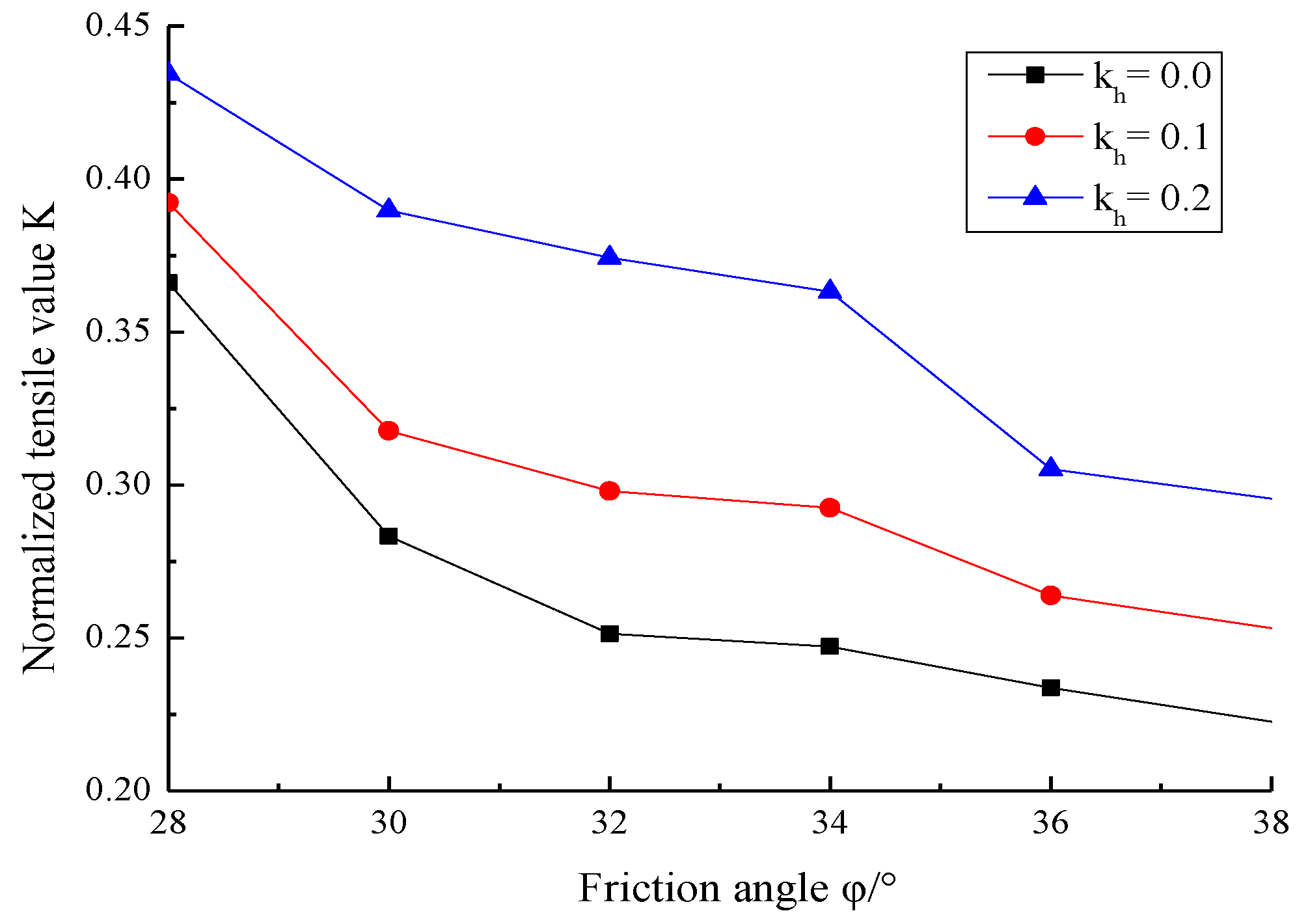
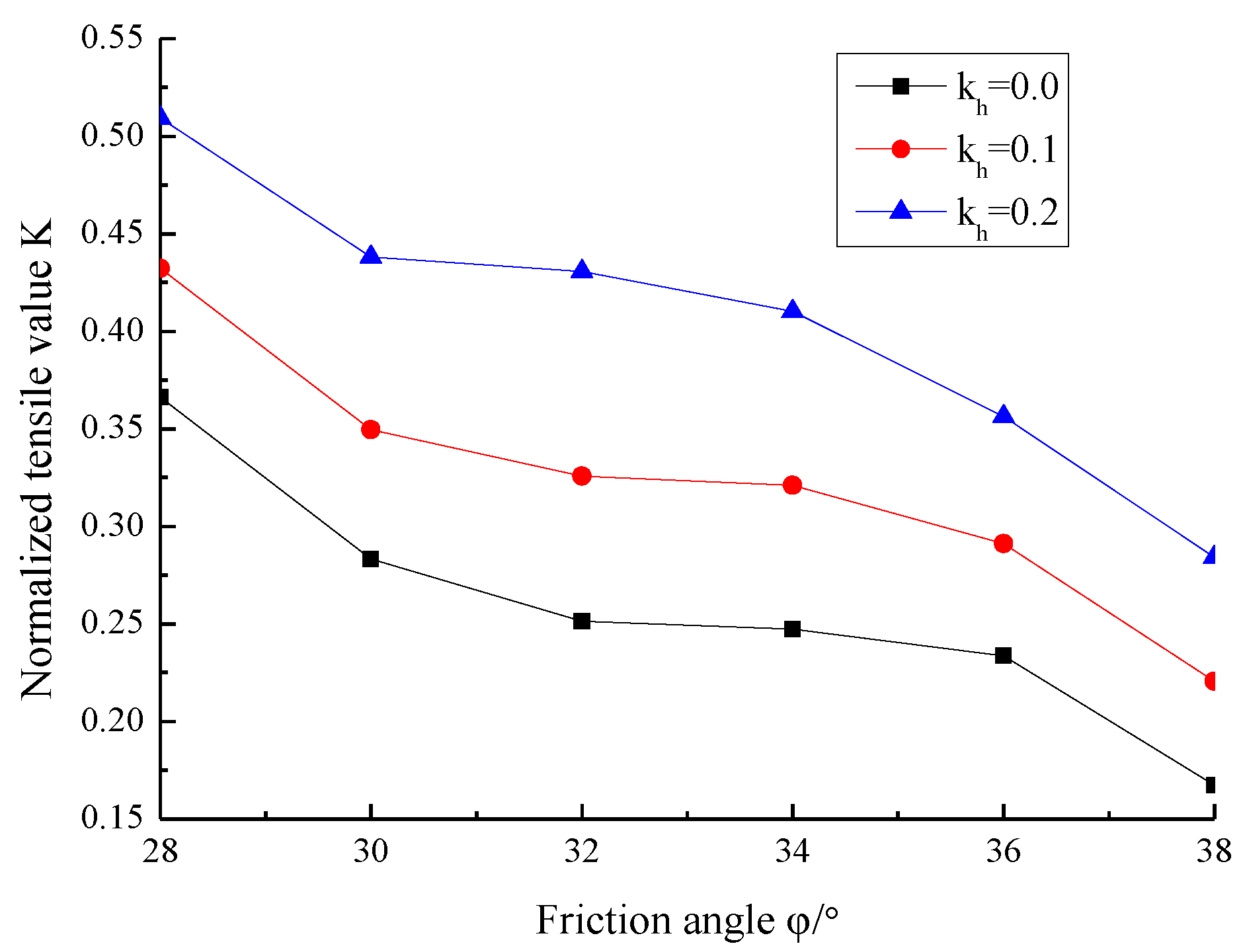
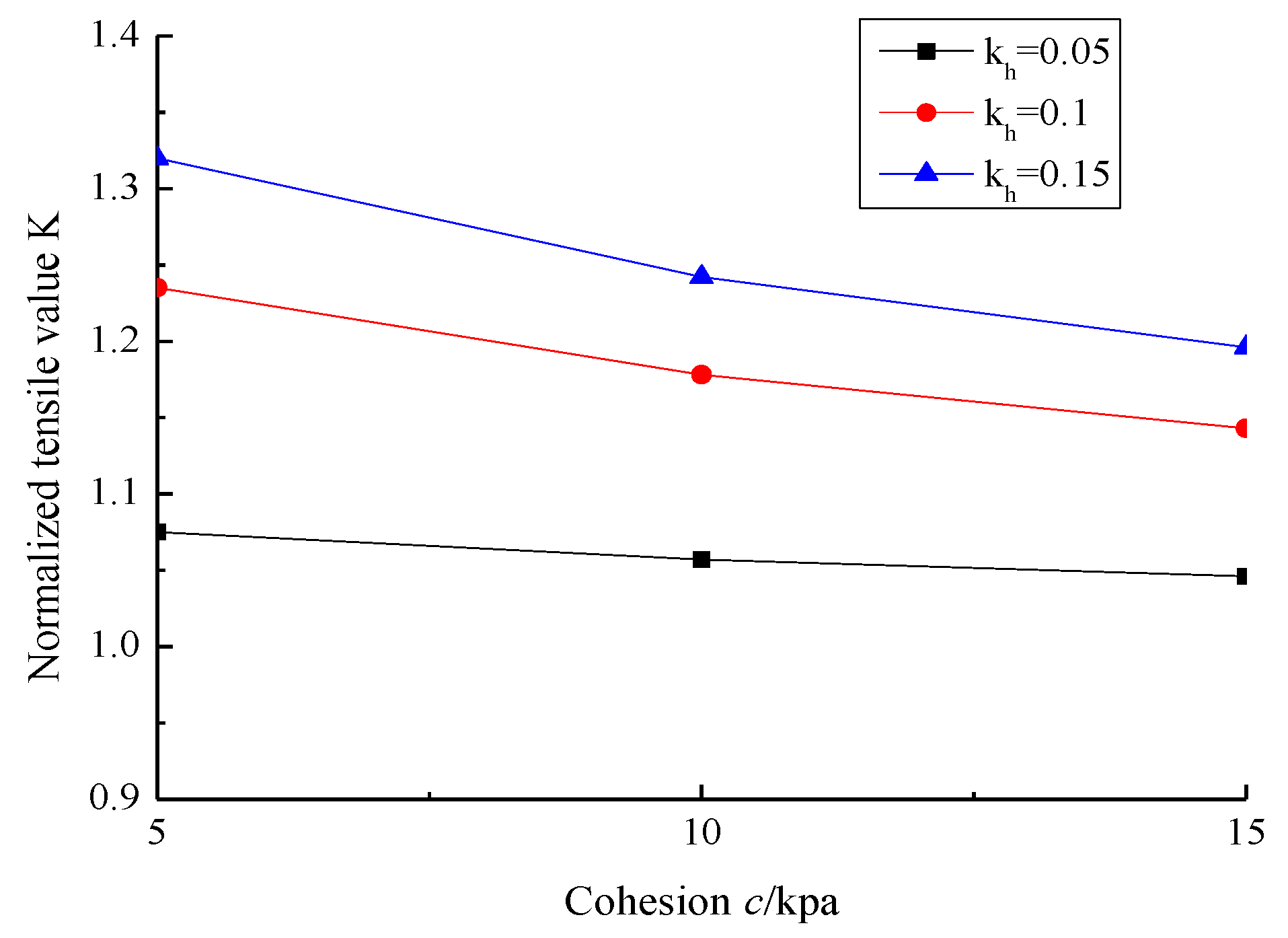
5.1. Influence of Seismic Acceleration Coefficients
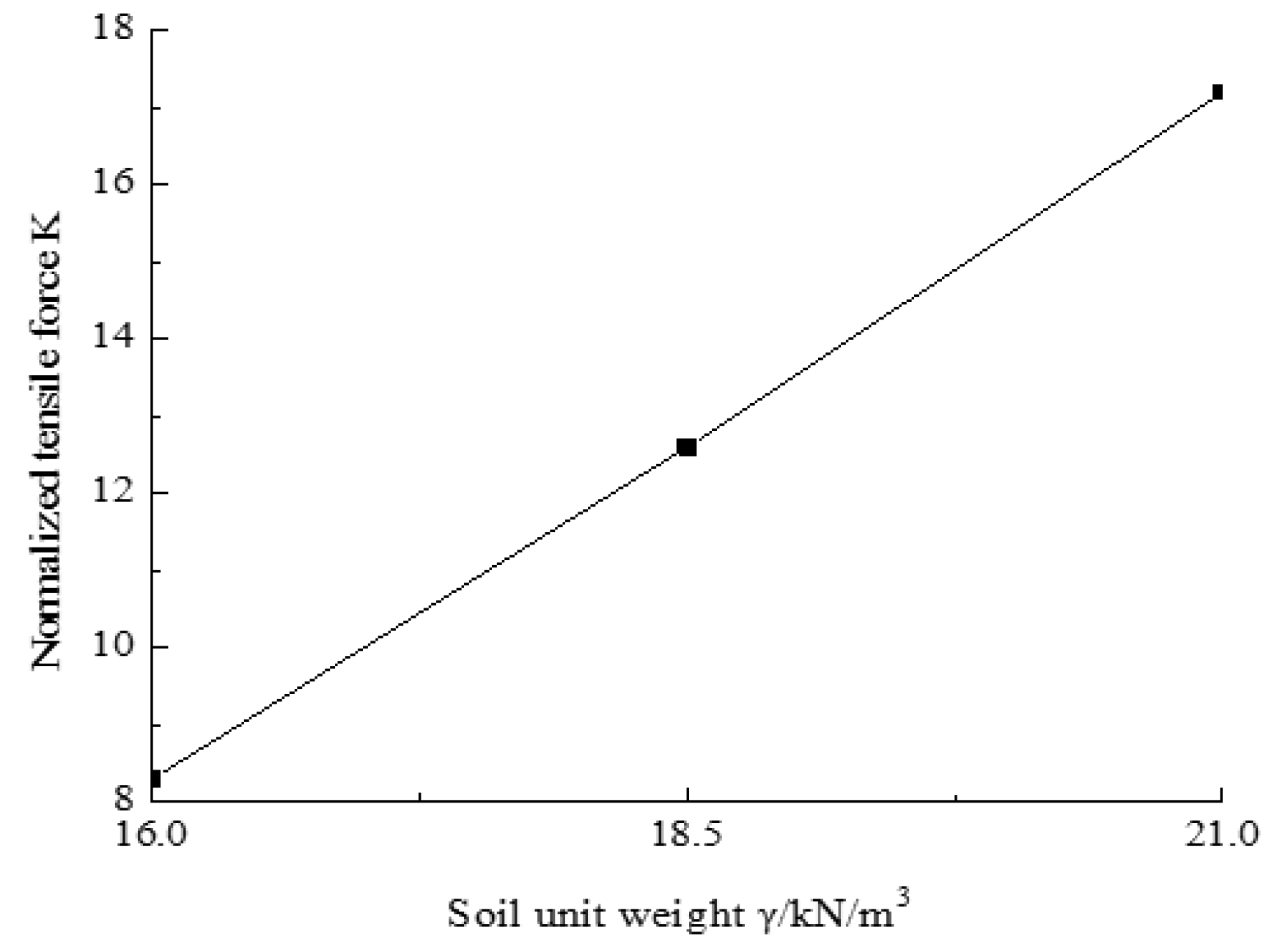
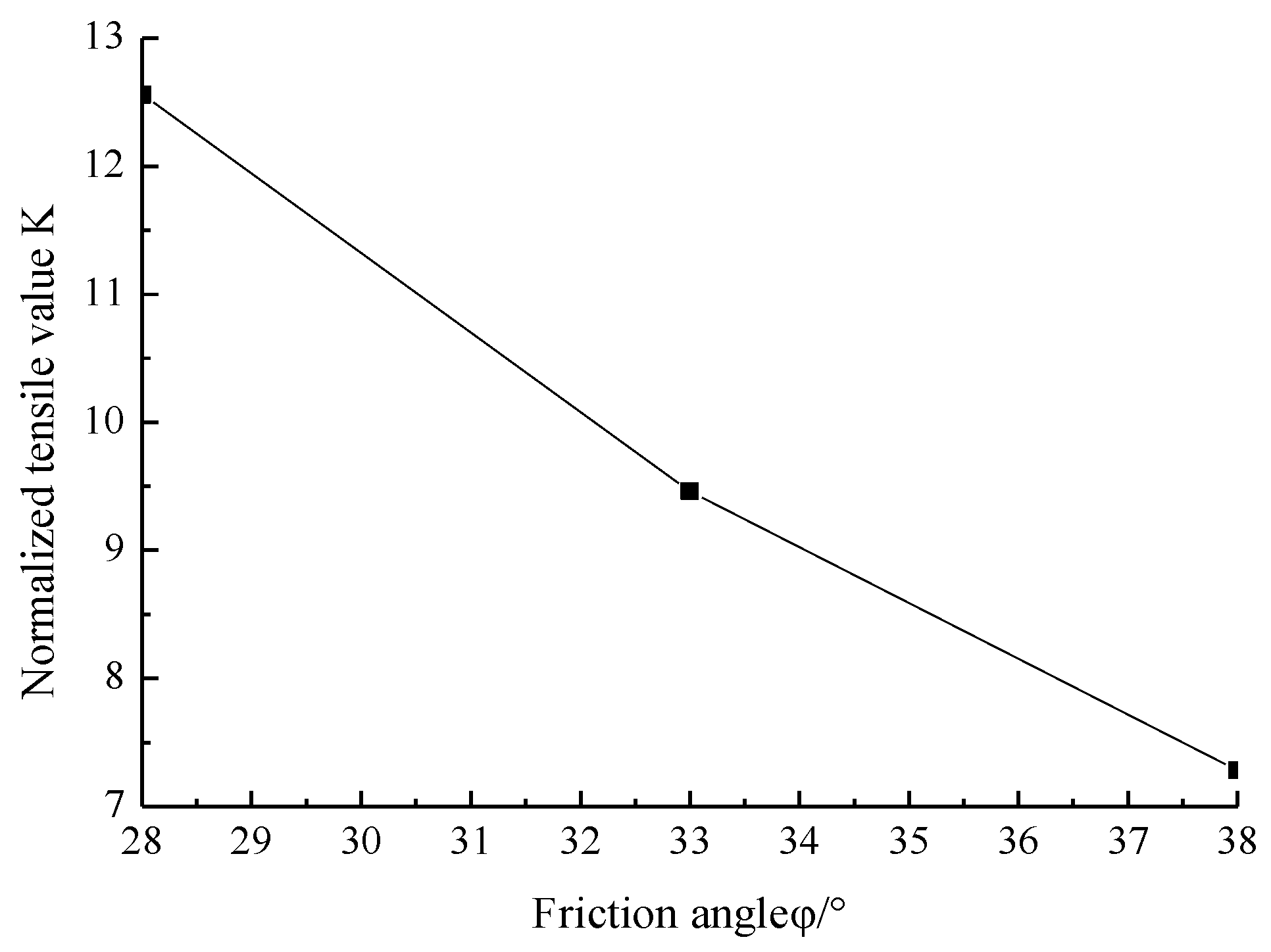
5.2. Influence of Soil Parameters
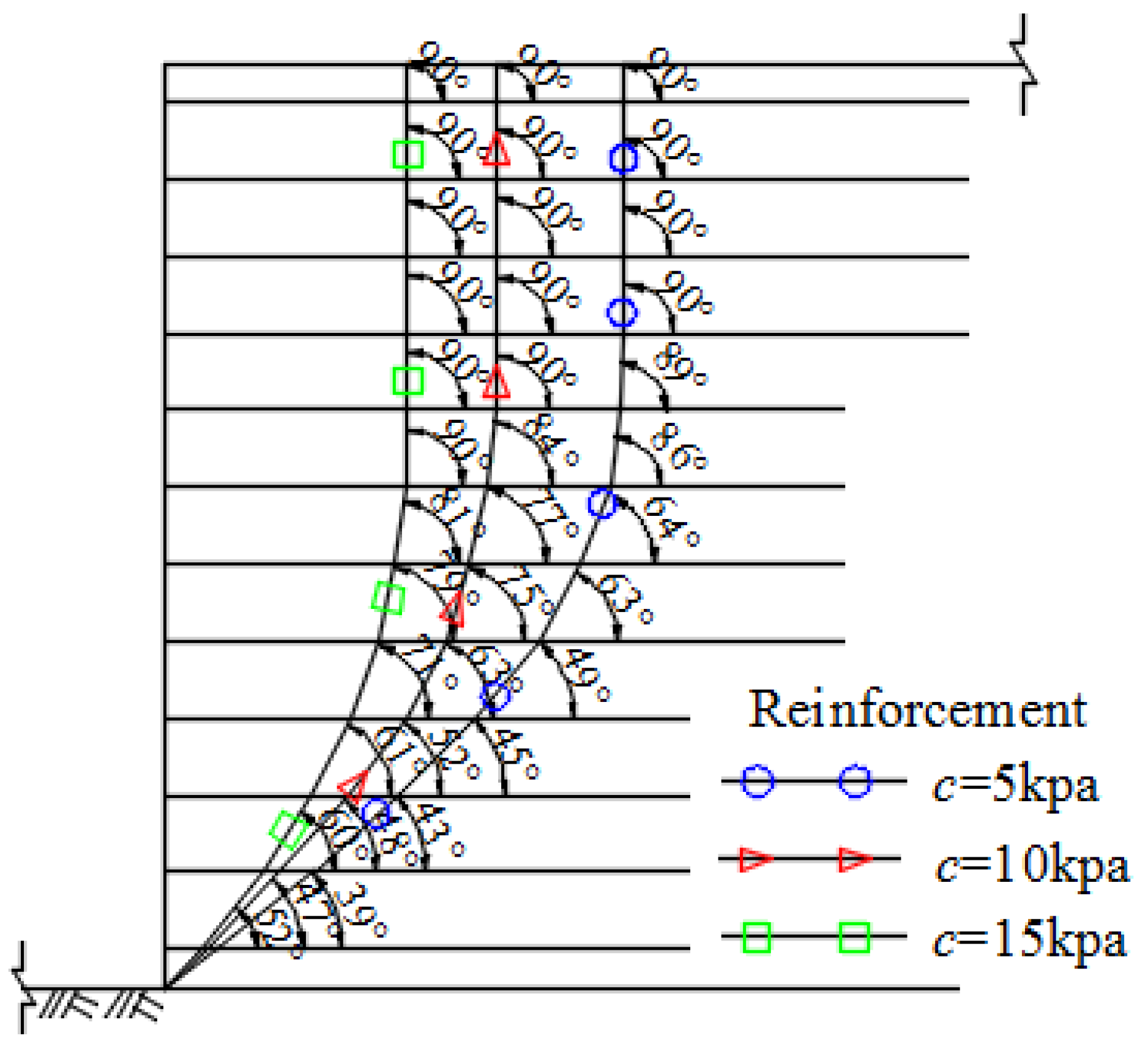
5.3. Influence of the Reinforcing Structure
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| St,i | shear force acting on the ith slice | τf | shear strength on the sliding surface |
| NN,i | normal force acting on the ith slice | τr | shear stress on the sliding surface |
| lai | length of reinforcement in the slip zone behind the wall | kv | vertical seismic coefficient |
| lei | length of reinforcement in the anchorage zone | kh | horizontal seismic coefficient |
| FN,i | normal force acting on the top of the ith slice | αh | horizontal seismic acceleration |
| FN,i+1 | normal force acting on the bottom of the ith slice | αv | vertical seismic acceleration |
| Qhi | horizontal seismic force acting on the top of the slice | H | height of wall |
| Qvi | vertical seismic force acting on the top of the slice | maximum sum of forces to maintain stability of the reinforced wall | |
| αi | inclination angle of slip surface of the slice and horizontal direction | Ti | tensile force of ith layer reinforcement |
| Wi | weight of the ith slice | K | normalized form of required total force to maintain stability of the wall |
| Sy,j | vertical distance between reinforcements | γ | soil density |
| n | number of reinforcement layers | φ | soil friction angle |
| Fs | safety for each slice | c | soil cohesion |
| hj | vertical distance between jth reinforcement and the top of the wall |
References
- Bathurst, R.J.; Hatami, K. Seismic response analysis of a geosynthetic-reinforced soil retaining wall. Geosynth. Int. 1998, 5, 127–166. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, W.; Jia, P.J.; Han, J.Y.; Guan, Y.P. Dynamic behavior of an embedded foundation under horizontal vibration in a poroelastic half-Space. Appl. Sci. 2019, 9, 740. [Google Scholar] [CrossRef]
- Subramaniam, P.; Banerjee, S. Factors affecting shear modulus degradation of cement treated clay. Soil Dyn. Earthq. Eng. 2014, 65, 181–188. [Google Scholar] [CrossRef]
- Ngo, V.L.; Kim, J.M.; Chang, S.H.; Lee, C. Effect of height ratio and mass ratio on structure-soil-structure interaction of two structures using centrifugal experiment. Appl. Sci. 2019, 9, 526. [Google Scholar] [CrossRef]
- Liu, S.Q.; Huang, X.W.; Zhou, A.Z.; Hu, J.; Wang, W. Soil-rock slope stability analysis by considering the non-uniformity of rocks. Math. Probl. Eng. 2018, 2018, 3121604. [Google Scholar] [CrossRef]
- Qin, C.; Chian, S.C. New perspective on seismic slope stability analysis. Int. J. Geomech. 2018, 18, 06018013. [Google Scholar] [CrossRef]
- Lu, W.H.; Miao, L.C.; Zhang, J.H.; Zhang, Y.X.; Li, J. Characteristics of deformation and damping of cement treated and expanded polystyrene mixed lightweight subgrade fill under cyclic load. Appl. Sci. 2019, 9, 167. [Google Scholar] [CrossRef]
- Zhang, L.; Goh, S.H.; Liu, H. Seismic response of pile-raft-clay system subjected to a long-duration earthquake: Centrifuge test and finite element analysis. Soil Dyn. Earthq. Eng. 2017, 92, 488–502. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, H. Seismic response of clay-pile-raft-superstructure systems subjected to far-field ground motions. Soil Dyn. Earthq. Eng. 2017, 101, 209–224. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L. Seismic response of pile–raft system embedded in spatially random clay. Géotechnique 2018. [Google Scholar] [CrossRef]
- Okabe, S. General theory on earth pressure and seismic stability of retaining wall and dam. J. Jpn. Soc. Civ. Eng. 1924, 10, 1277–1323. [Google Scholar]
- Basha, B.M.; Babu, G.S. Seismic rotational displacements of gravity walls by pseudodynamic method with curved rupture surface. Int. J. Geomech. 2009, 10, 93–105. [Google Scholar] [CrossRef]
- Zeng, X.; Steedman, R.S. On the behaviour of quay walls in earthquakes. Géotechnique 1993, 43, 417–431. [Google Scholar] [CrossRef]
- Ling, H.I.; Leshchinsky, D. Effects of vertical acceleration on seismic design of geosynthetic-reinforced soil structures. Géotechnique 1998, 48, 347–373. [Google Scholar] [CrossRef]
- Kwak, C.; Park, J.; Jang, D.; Park, I. Dynamic shear degradation of geosynthetic–soil interface in waste landfill sites. Appl. Sci. 2017, 7, 1225. [Google Scholar] [CrossRef]
- Shahgholi, M.; Fakher, A.; Jones, C.J.F.P. Horizontal slice method of analysis. Géotechnique 2001, 51, 881–885. [Google Scholar] [CrossRef]
- Choudhury, D.; Singh, S. New approach for estimation of static and seismic active earth pressure. Geotech. Geol. Eng. 2006, 24, 117–127. [Google Scholar] [CrossRef]
- El-Emam, M.M.; Bathurst, R.J. Experimental design, instrumentation and interpretation of reinforced soil wall response using a shaking table. Int. J. Phys. Model. Geotech. 2004, 4, 13–32. [Google Scholar] [CrossRef]
- Guler, E.; Enunlu, A.K. Investigation of dynamicbehavior of geosynthetic reinforced soil retaining structures under earthquake loads. Bull. Earthq. Eng. 2009, 7, 737–777. [Google Scholar] [CrossRef]
- Jia, L.; Zhu, Y.; Lai, C. Stability analysis of reinforced earth retaining wall under earthquake. J. Southwest Jiao Tong Univ. 2016, 51, 698–703. (In Chinese) [Google Scholar]
- Jia, L.; Guo, J.; Yao, K. Seismic stability analysis of reinforced soil slope using horizontal slice method. J. Basic Sci. Eng. 2018, 26, 168–176. (In Chinese) [Google Scholar]
- Lo, S.R.; Xu, D.W. A strain-based design method for the collapse limit state of reinforced soil walls or slopes. Can. Geotech. J. 1992, 29, 832–842. [Google Scholar] [CrossRef]
- Nouri, H.; Fakher, A.; Jones, C.J.F.P. Development of horizontal slice method for seismic stability analysis of reinforced slopes and walls. Geotext. Geomembr. 2006, 24, 175–187. [Google Scholar] [CrossRef]
- Jiang, J.; Yang, G. A New Slice Method for Seismic Stability Analysis of Reinforced Retaining Wall. In Computational Structural Engineering; Springer: Dordrecht, The Netherlands, 2009; pp. 167–172. [Google Scholar]
- Lin, Y.-L.; Leng, W.-M.; Yang, G.-L.; Zhao, L.-H.; Li, L.; Yang, J.-S. Seismic active earth pressure of cohesive-frictional soil on retaining wall based on a slice analysis method. Soil Dyn. Earthq. Eng. 2015, 70, 133–147. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, C.; Wu, Y.; Li, D.; Zhang, F. Evaluation of oblique pullout resistance of reinforcements in soil wall subjected to seismic loads. Geotext. Geomembr. 2014, 42, 515–524. [Google Scholar] [CrossRef]
- Lin, Y.; Cheng, X.; Yang, G. Shaking table test and numerical simulation on a combined retaining structure response to earthquake loading. Soil Dyn. Earthq. Eng. 2018, 108, 29–45. [Google Scholar] [CrossRef]
- Cakir, T. Evaluation of the effect of earthquake frequency content on seismic behavior of cantilever retaining wall including soil–structure interaction. Soil Dyn. Earthq. Eng. 2013, 45, 96–111. [Google Scholar] [CrossRef]
- Peng, J.; Zhu, Y.; Zhou, Y. Derivation of Shukla’s generalized expression of seismic passive earth pressure on retaining walls with cohesive-frictional backfill by the inclined slice element method. Soil Dyn. Earthq. Eng. 2018, 114, 225–228. [Google Scholar] [CrossRef]
- Trandafir, A.C.; Kamai, T.; Sidle, R.C. Earthquake-induced displacements of gravity retaining walls and anchor-reinforced slopes. Soil Dyn. Earthq. Eng. 2009, 29, 428–437. [Google Scholar] [CrossRef]
- Askari, F.; Totonchi, A.; Farzaneh, O. Application of admissible stress fields for computation of passive seismic force in retaining walls. Sci. Iran. 2012, 19, 967–973. [Google Scholar] [CrossRef] [Green Version]
- Nouri, H.R.; Fakher, A. The Effect of Amplification on the Seismic Stability of Reinforced Soil Slopes Using Horizontal Slice Method. Geotech. Earthquake Eng. Soil Dyn. IV 2008, 1–10. [Google Scholar] [CrossRef]
- Ahmad, S.M.; Choudhury, D. Pseudo-dynamic approach of seismic design for waterfront reinforced soil-wall. Geotext. Geomembr. 2008, 26, 291–301. [Google Scholar] [CrossRef]
- Nimbalkar, S.S.; Choudhury, D.; Mandal, J.N. Seismic stability of reinforced soil-wall by pseudo-dynamic method. Geosynth. Int. 2006, 13, 111–119. [Google Scholar] [CrossRef]
- Reddy, G.N.; Madhav, M.R.; Reddy, E.S. Pseudo-static seismic analysis of reinforced soil wall—Effect of oblique displacement. Geotext. Geomembr. 2008, 26, 393–403. [Google Scholar] [CrossRef]
- Boulanger, R.W. Seismic Design Guidelines for Port Structures. Earthq. Spectra 2002, 18, 579–580. [Google Scholar] [CrossRef]
- GuhaRay, A.; Baidya, D.K. Reliability coupled sensitivity-based seismic analysis of gravity retaining wall using Pseudostatic approach. J. Geotech. Geoenviron. Eng. 2016, 142, 04016010. [Google Scholar] [CrossRef]
- Shekarian, S.; Ghanbari, A. A pseudo-dynamic method to analyzeretaining wall with reinforced and unreinforced backfill. J. Seismol. Earthq. Eng. 2008, 10, 41–46. [Google Scholar]
- Nouri, H.; Fakher, A.; Jones, C.J.F.P. Evaluating the effects of the magnitude and amplificationof pseudo-static acceleration on reinforced soil slopes and wallsusing the limit equilibrium Horizontal Slices Method. Geotext. Geomembr. 2008, 26, 263–278. [Google Scholar] [CrossRef]
- Syed, M.; Deepankar, C. Seismic internal stability analysis of waterfront reinforced-soil wall using pseudo-static approach. Ocean Eng. 2012, 52, 83–90. [Google Scholar]
- Chandaluri, V.K.; Sawant, V.A.; Shukla, S.K. Seismic Stability Analysis of Reinforced Soil Wall Using Horizontal Slice Method. Int. J. Geosynth. Ground Eng. 2015, 1, 23. [Google Scholar] [CrossRef]





| Characteristics | Value | Average Value |
|---|---|---|
| Reinforced retaining wall height (H) | 6 m | — |
| Soil density () | 16–21 kN/m3 | 18.5 kN/m3 |
| Soil cohesion (c) | 0–15 kN/m2 | 10 kN/m2 |
| Internal angle of soil friction () | 28–38° | 33° |
| Coefficient of horizontal seismic acceleration () | 0, 0.1, 0.2, 0.3 | 0.15 |
| Coefficient of vertical seismic acceleration () | 0, 0.05, 0.1, 0.15 | 0.075 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, L.; He, S.; Li, N.; Wang, W.; Yao, K. Stability of Reinforced Retaining Wall under Seismic Loads. Appl. Sci. 2019, 9, 2175. https://doi.org/10.3390/app9112175
Jia L, He S, Li N, Wang W, Yao K. Stability of Reinforced Retaining Wall under Seismic Loads. Applied Sciences. 2019; 9(11):2175. https://doi.org/10.3390/app9112175
Chicago/Turabian StyleJia, Liang, Shikai He, Na Li, Wei Wang, and Kai Yao. 2019. "Stability of Reinforced Retaining Wall under Seismic Loads" Applied Sciences 9, no. 11: 2175. https://doi.org/10.3390/app9112175
APA StyleJia, L., He, S., Li, N., Wang, W., & Yao, K. (2019). Stability of Reinforced Retaining Wall under Seismic Loads. Applied Sciences, 9(11), 2175. https://doi.org/10.3390/app9112175






