Underwater 2D Image Acquisition Using Sequential Striping Illumination
Abstract
:1. Introduction
2. Approach of Image Recovery from Sequential Striping Illuminated Images
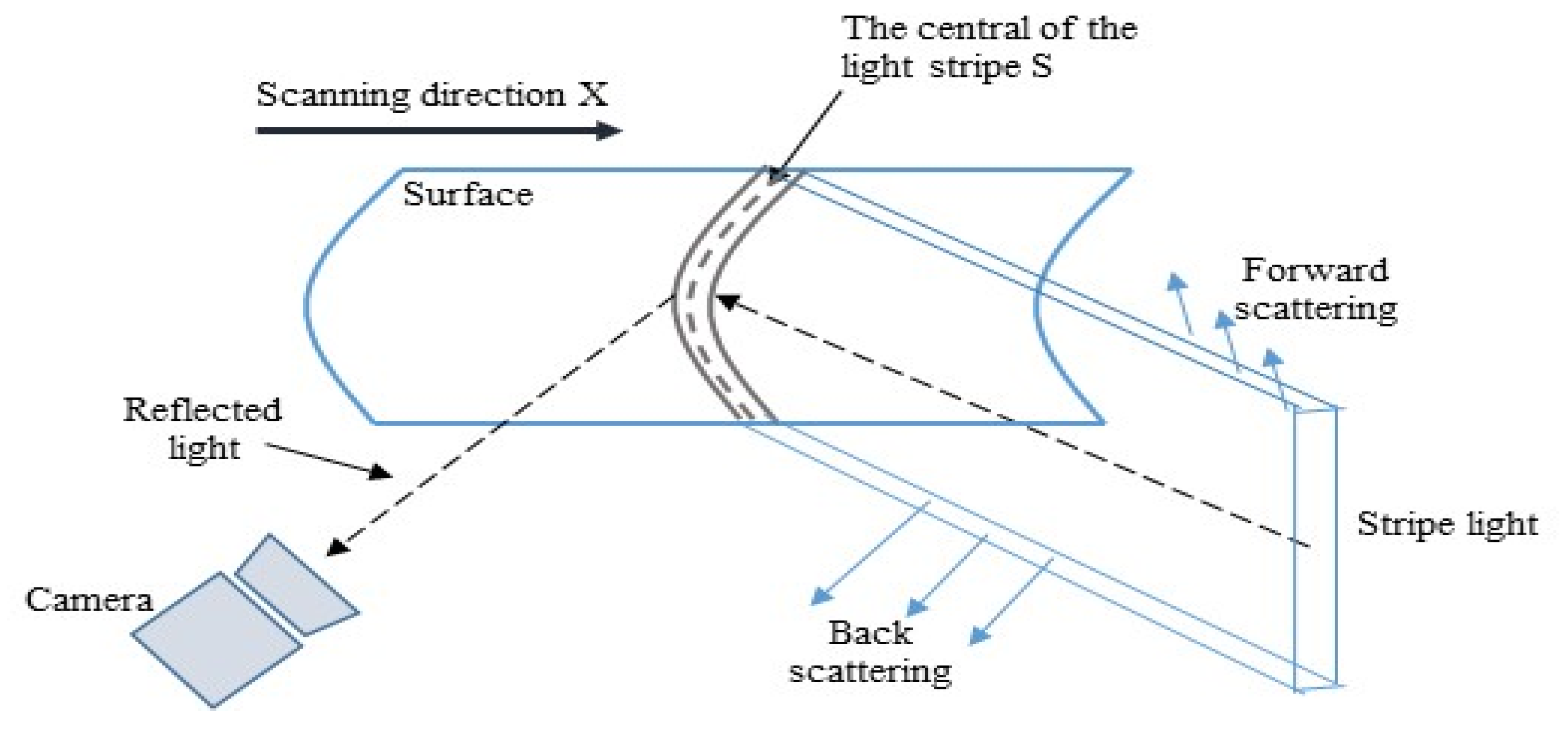
2.1. Image Formation Model
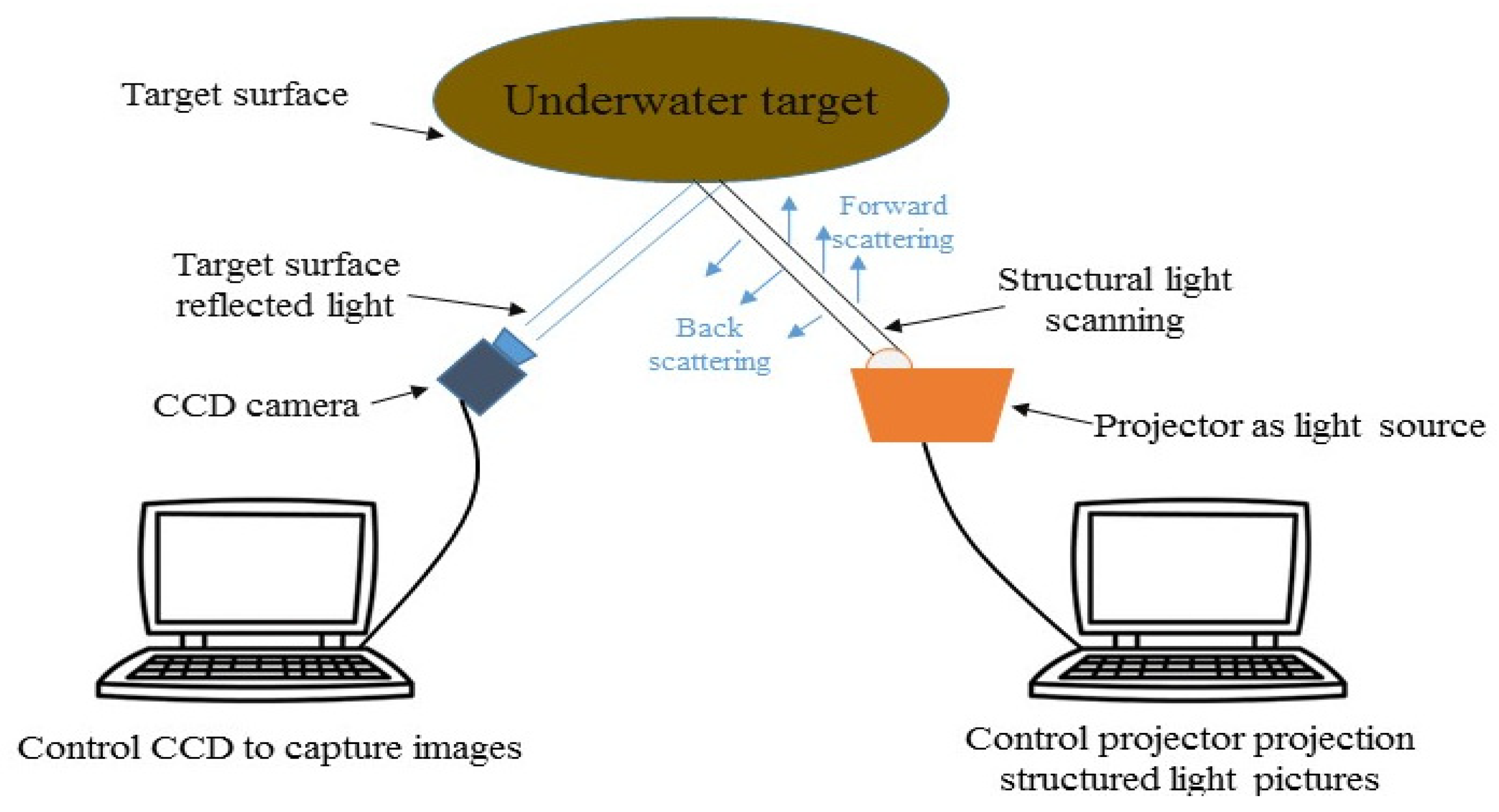
2.2. System Implementation
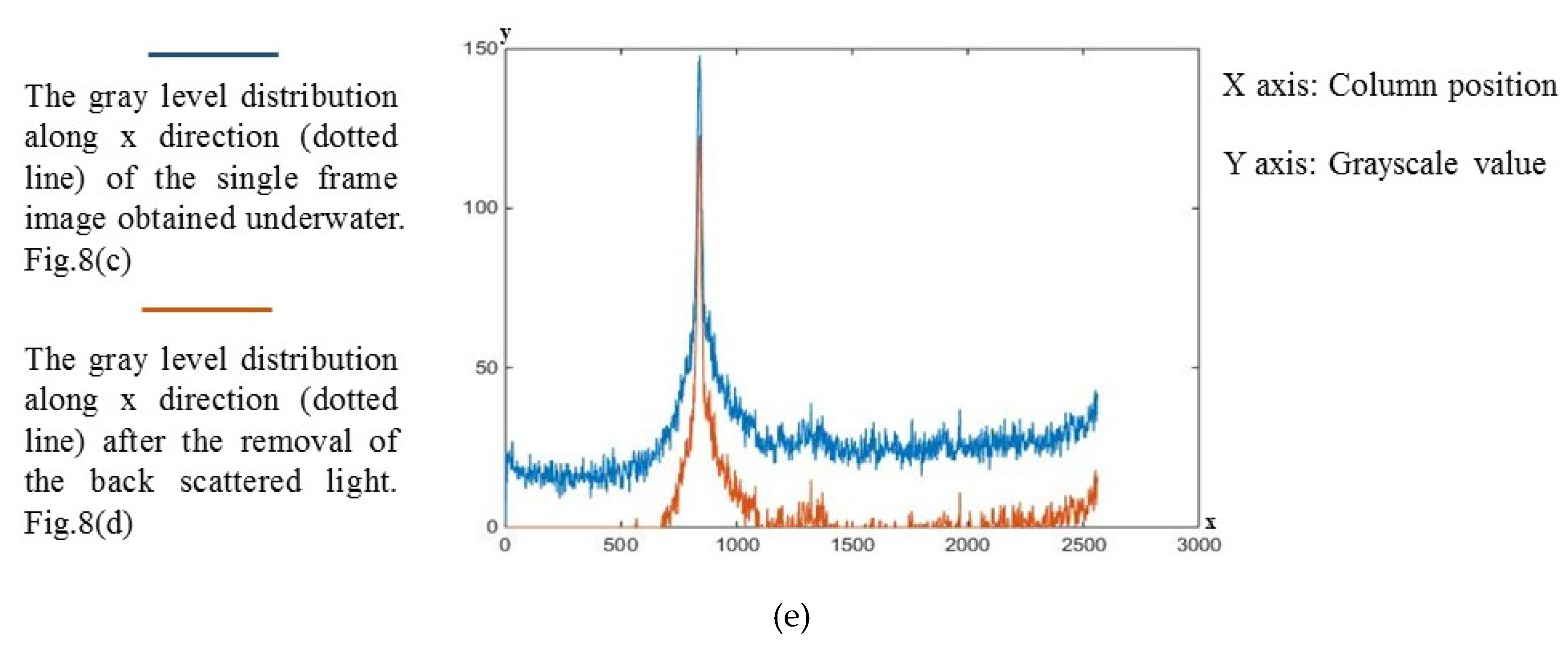
3. Removal of Back Scattered Light
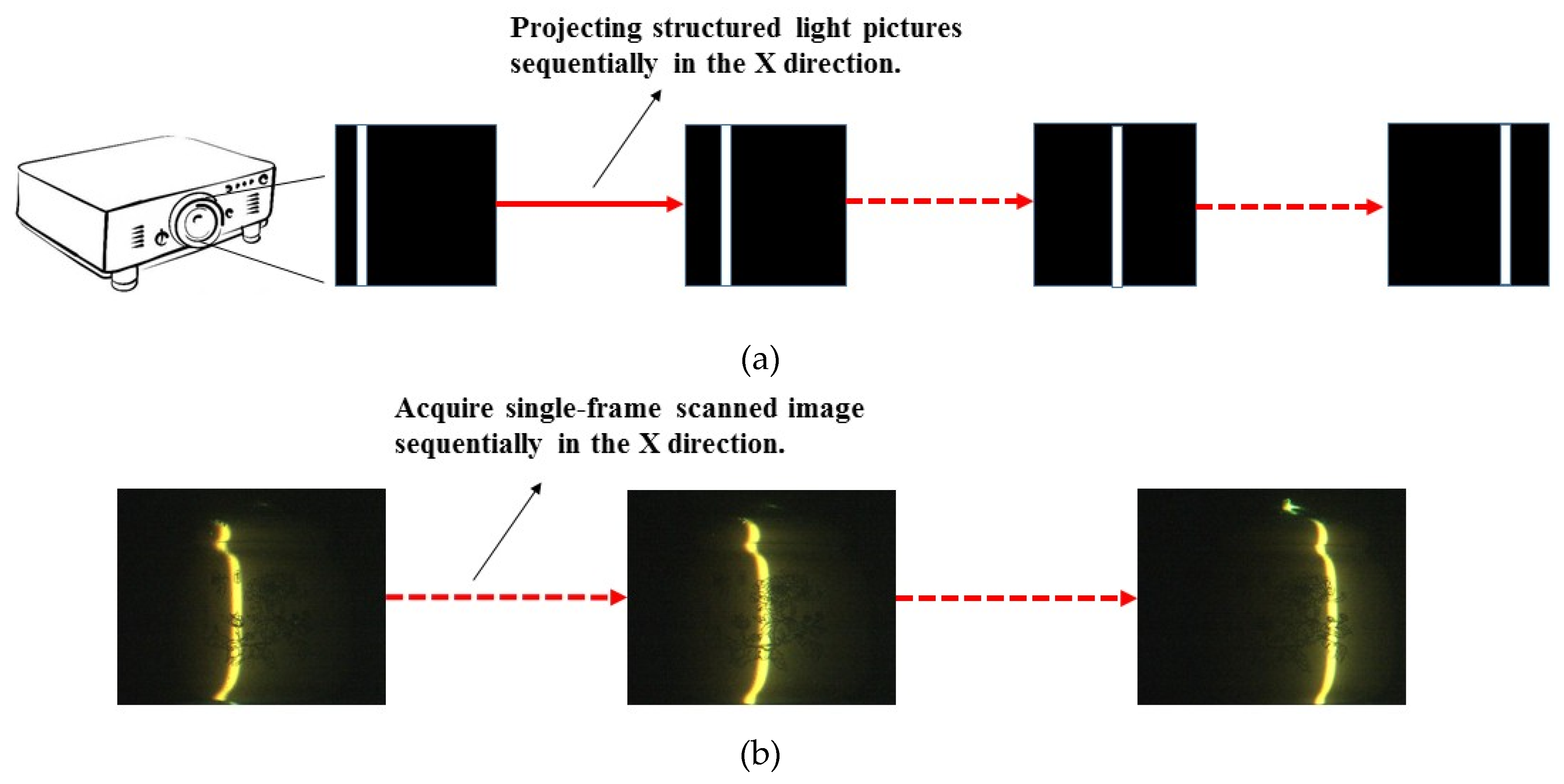
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Coles, B.W.J. Laser line scan systems as environmental survey tools. Ocean News Technol. 1997, 3, 22–27. [Google Scholar]
- Moore, K.D.; Jaffe, J.S. Time Evolution of High-resolution Topographic Measurement of the Sea Floor Using a 3D Laser Line Scan Mapping System. J. Ocean Eng. 2001, 27, 525–545. [Google Scholar] [CrossRef]
- Carder, K.; Reinersman, P.; Costello, D.; Kaltenbacher, E.; Kloske, J.; Montes, M. Optical inspection of ports and harbors: Laser-line sensor model applications in 2 and 3 dimensions. In Proceedings of the SPIE, Photonics for Port and Harbor Security; SPIE Digital Library: Bellingham, WA, USA, 2005; Volume 5780, pp. 49–58. [Google Scholar]
- Dalgleish, F.R.; Tetlow, S.; Allwood, R.L. Seabed-relative navigation by structured lighting techniques. In Advances in Unmanned Marine Vehicles; Roberts, G.N., Peter, S.R., Eds.; Peregrinus Ltd., Herts.: Estero, FL, USA, 2005; Chapter 13; pp. 277–292. [Google Scholar]
- Je, C.; Lee, S.W.; Park, R.H. High-contrast color-stripe pattern for rapid structured-light range imaging. In Proceedings of the Computer Vision—ECCV 2004 8th European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004. [Google Scholar]
- Jaffe, J.S.; Moore, K.D.; Mclean, J.; Strand, M.P. Underwater Optical Imaging: Status and Prospects. Oceanography 1997, 14, 64–75. [Google Scholar] [CrossRef]
- Yousefi, B.; Mirhassani, S.M.; AhmadiFard, A.; Hosseini, M. Hierarchical segmentation of urban satellite imagery. Int. J. Appl. Earth Obs. Geoform. 2014, 30, 158–166. [Google Scholar] [CrossRef]
- Dalgleish, F.R.; Caimi, F.M.; Britton, W.B.; Andren, C.F. Improved LLS imaging performance in scattering-dominant water. In Proceedings of the SPIE 7317 Ocean Sensing and Monitoring, Orlando, FL, USA, 29 April 2009. [Google Scholar]
- Zheng, B.; Liu, B.; Zhang, H.; Gulliver, T.A. A laser digital scanning grid approach to three dimensional real-time detection of underwater targets. In Proceedings of the IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, Victoria, BC, Canada, 23–26 August 2009; pp. 798–801. [Google Scholar]
- Narasimhan, S.G.; Nayar, K.; Sun, B.; Koppal, S.J. Structured light in scattering media. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; Volume 1, pp. 420–427. [Google Scholar]
- Yousefi, B.; Mirhassani, S.M.; Hosseini, M.M.; Fatemi, M.J.R. A novel fuzzy based method for 3D buildings modelling in urban satellite imagery. In Proceedings of the IEEE Conference on Open Systems (ICOS2011), Langkawi, Malaysia, 25–28 September 2011. [Google Scholar]
- Lam, E.; Goodman, J.W. Iterative statistical approach to blind image deconvolution. J. Opt. Soc. Am. 2000, 17, 1177–1184. [Google Scholar] [CrossRef]
- Zege, E.P.; Ivanov, A.P.; Katsev, I.L. Image Transfer through a Scattering Medium; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Jaffe, J.S. Computer Modeling and the Design of Optimal Underwater Imaging Systems. IEEE J. Ocean Eng. 1990, 15, 101–111. [Google Scholar] [CrossRef]
- Richardson, W.H. Bayesian-Based Iterative Method of Image Restoration. J. Opt. Soc. Am. 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Lucy, L.B. An iterative technique for the rectification of observed distributions. Astron. J. 1974, 79, 745–754. [Google Scholar] [CrossRef]
- Wang, R.; Wang, G. Single image recovery in scattering medium by propagating deconvolution. Opt. Express 2014, 22, 8114–8119. [Google Scholar] [CrossRef] [PubMed]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, B.; Wang, G. Underwater 2D Image Acquisition Using Sequential Striping Illumination. Appl. Sci. 2019, 9, 2179. https://doi.org/10.3390/app9112179
Gong B, Wang G. Underwater 2D Image Acquisition Using Sequential Striping Illumination. Applied Sciences. 2019; 9(11):2179. https://doi.org/10.3390/app9112179
Chicago/Turabian StyleGong, Benxing, and Guoyu Wang. 2019. "Underwater 2D Image Acquisition Using Sequential Striping Illumination" Applied Sciences 9, no. 11: 2179. https://doi.org/10.3390/app9112179
APA StyleGong, B., & Wang, G. (2019). Underwater 2D Image Acquisition Using Sequential Striping Illumination. Applied Sciences, 9(11), 2179. https://doi.org/10.3390/app9112179



