Development of A Loss Minimization Based Operation Strategy for Embedded BTB VSC HVDC
Abstract
:1. Introduction
2. System Description
2.1. Korean Power System
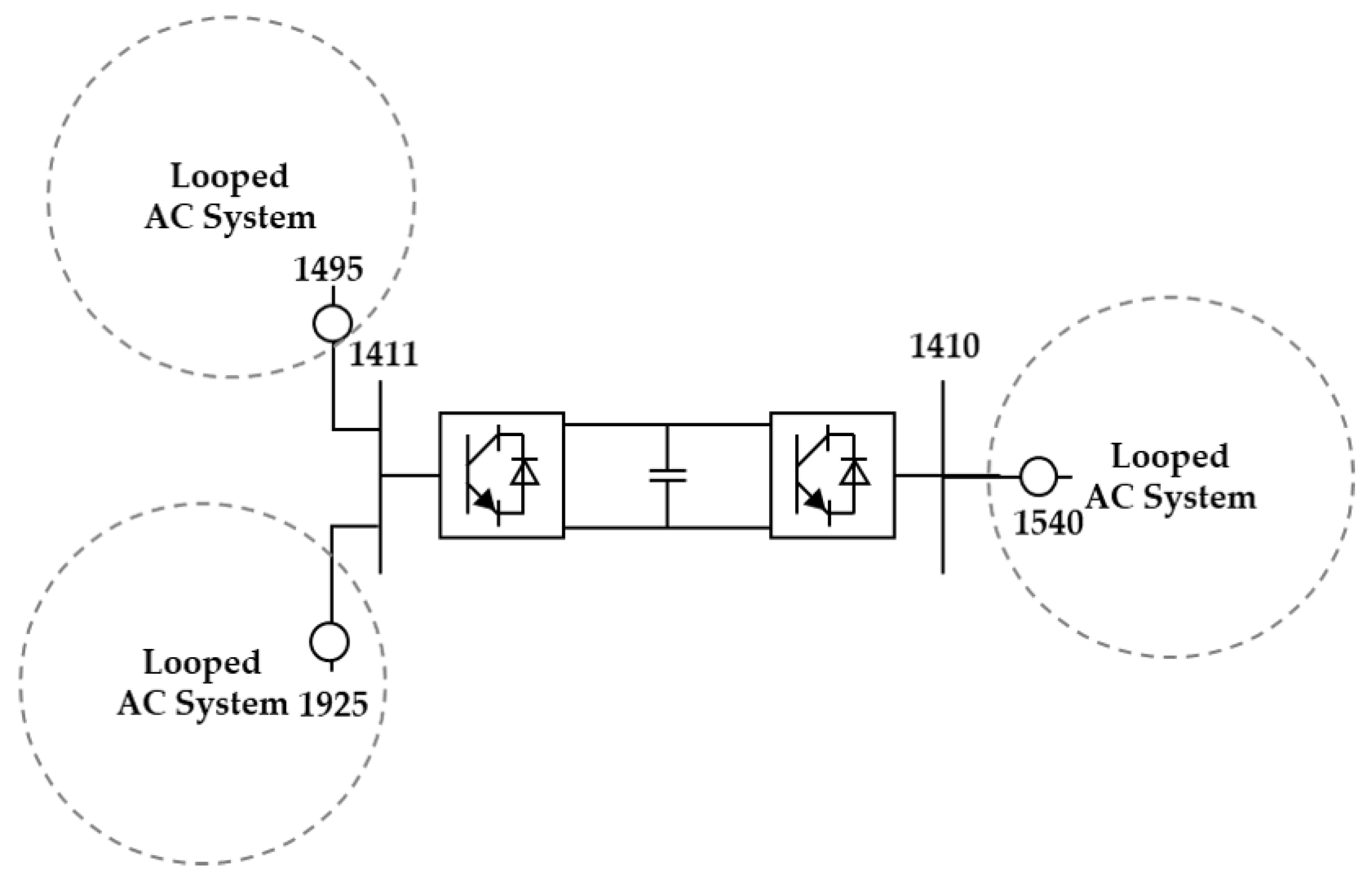
2.2. Embedded BTB HVDC Siting in Meshed System
- is a fault current at the fault point n;
- is a pre-fault voltage at the fault point n;
- is a thevenin impedance at the fault point n; and
- is a fault impedance at the fault point n;
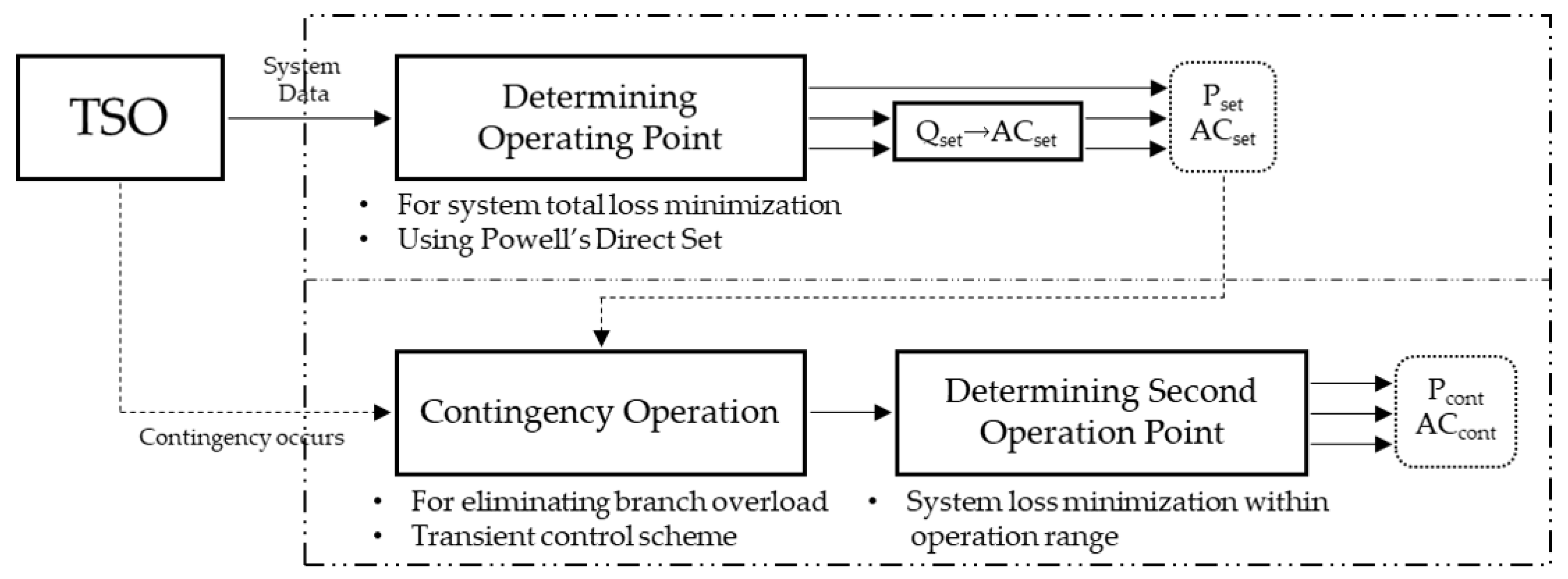
2.3. Proposed Control Scheme
3. Determination of Embedded HVDC Operation Point
3.1. System Total-Loss Minimization (STLM) Control
- System total-loss minimization
- Voltage criteria
- Branch overloads
3.1.1. System Total-Loss Minimization
- is the system total loss;
- is the AC system loss;
- is the HVDC line loss;
- is the HVDC conversion loss;
- are the AC/DC line flow active powers at the receiving end;
- is the DC line flow active powers at the sending end;
- is the AC line flow reactive powers at the receiving end;
- are the AC/DC voltage at the receiving end;
- are the resistance values of the AC/DC line; and
- is the loss rate of the converter.
3.1.2. Voltage Criteria
- is the minimum/maximum voltage at bus i; and
- is voltage at bus i.
3.1.3. Line Overload
- is the minimum/maximum power flow on line l; and
- is power flow on line l.
- is the PTDF of line l with respect to bus m;
- is the amount of the power flow change in line l; and
- is the amount of the power change injected for bus m.
- is the power flow change of line l by HVDC control
- is the maximum variation of line l;
- is the reference value of line l;
- is the active power capacity of the HVDC;
- is the PTDF of line l with respect to the rectifier end;
- is the PTDF of line l with respect to the inverter end;
- is the capacity of line l; and
- is a weighting factor.
3.1.4. Application of Three-Dimensional Powell’s Direct Set (3-PDS)
- Set the initial point and the independent directions used for initial searching . We set the values as , .
- A conjugate direction should be generated within each iteration.
- -
- Starting from (k is the iteration number), sequentially search the directions in by finding the minimum.where is the step size.
- -
- A conjugate direction is generated after searching down by
- Update the search direction by adding directions to and replace the other direction. It is common to replace the first direction with a new , but in this application, since the control of active power is much more influential than the control of reactive power in loss reduction, so the direction of active power () is left and the new direction is updated. We can get .
- Find the new optimal operation point .
- Convergence check.
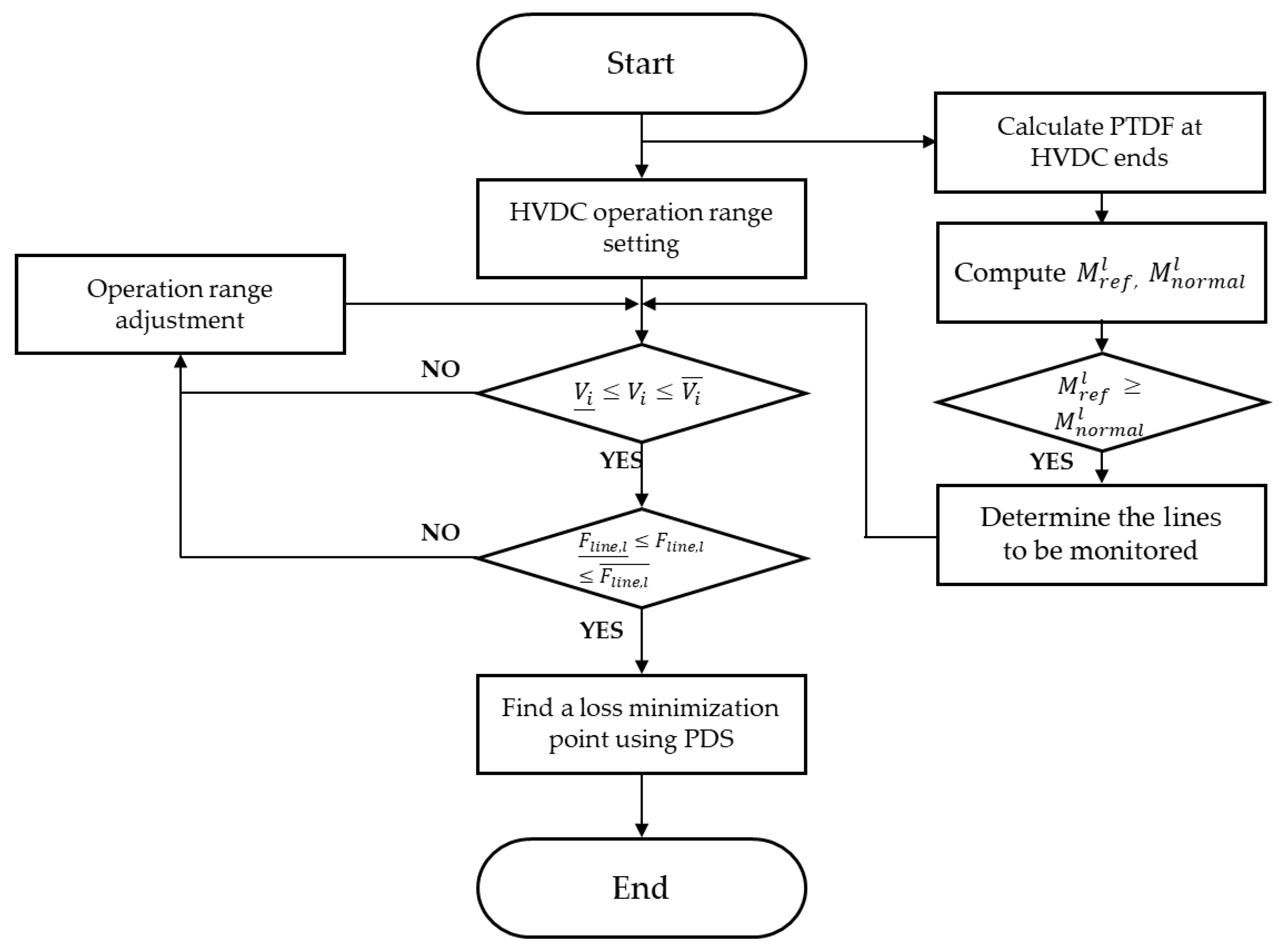
3.1.5. HVDC Operating Point with STLM Control
- The initial active/reactive power operation range is set with reference to the HVDC capacity.
- The number of branches to be monitored could be reduced using PTDF. These represent branches where the amount of power flow varies greatly with HVDC operating point (Section 3.1.3).
- The operating area should be adjusted so as not to deviate from the constraints. In the later operating point determination process, the operating range set here should not be exceeded.
- The operation point that minimizes the system total loss is determined using the PDS. The active/reactive power output determined in this process are respectively input into the active power set value and the AC voltage set value.
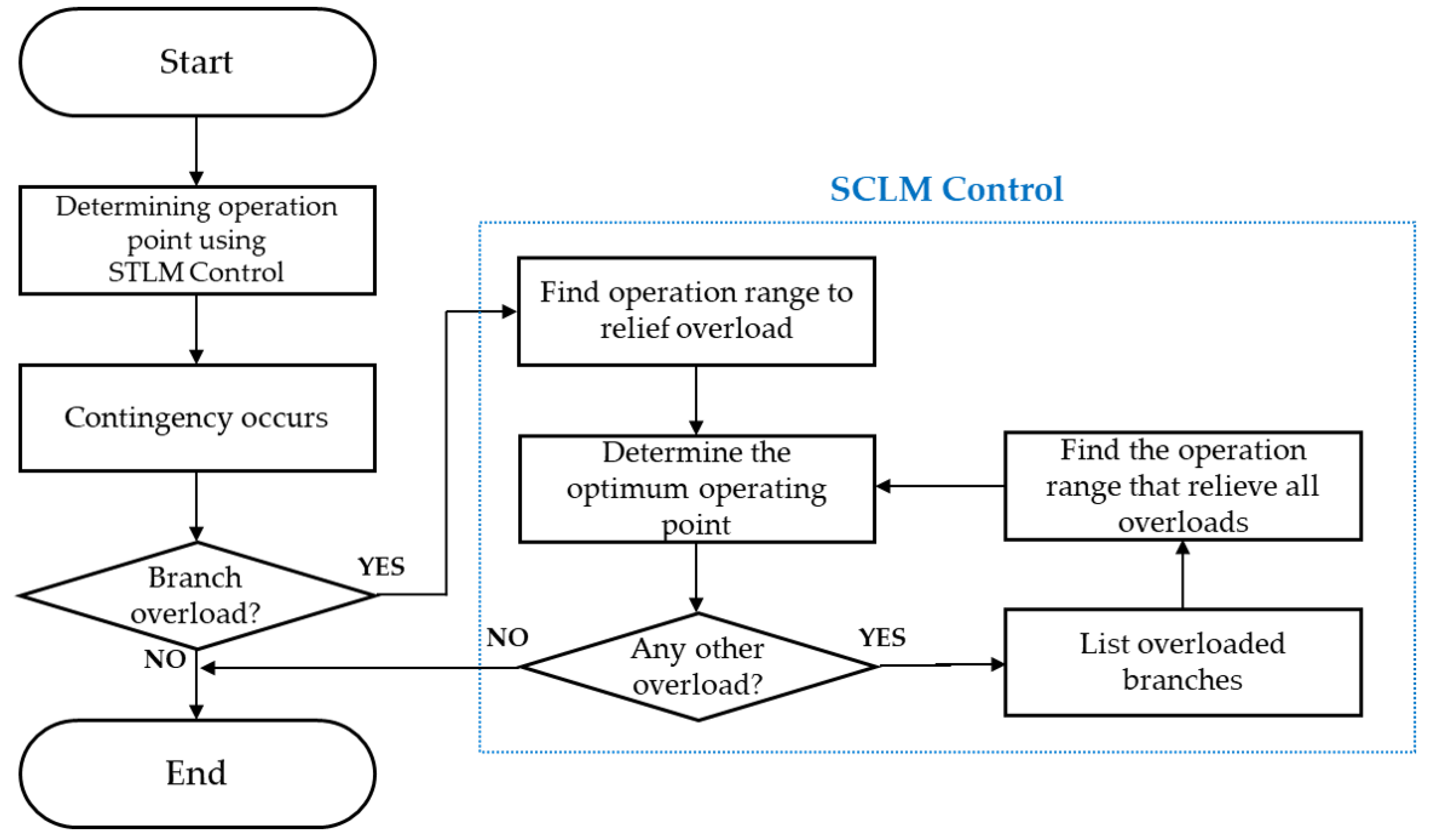
3.2. Security-Constrained Loss Minimization (SCLM) Control
- BTB VSC HVDC normally operates with the operating point calculated in Section 3.1.
- In the event of a contingency, it detects the overloads of the other line and calculates the operation range where the overload of the line can be eliminated.
- Within the previously determined operating area, a new operating point is calculated that minimizes losses and maintains system reliability.
- At this time, it is necessary to check whether the other lines are overloaded at the determined operating point. If there are overloads of other lines, an optimum operating point should be found in the operating area where the overloads of the line are eliminated.
4. Case Study
4.1. System Information
- The load in the metropolitan area is about 40% of the total load, and a large amount of power is supplied from the non-metropolitan area.
- In order to improve the system stability, it is configured as a looped system, and thereby the problem of fault current is serious.
- The 154kV Yangju bus (1410) will be separated and connected to VSC BTB HVDC to solve the fault current problems in the metropolitan area and to improve system stability.
4.2. BTB VSC HVDC Siting for Fault Current Reduction
4.3. STLM Strategy in Normal Condition
- Initial operating point : (0, 0, 0),
- Independent directions used for initial searching ,
- Step size .
4.4. SCLM Control in Transient Condition
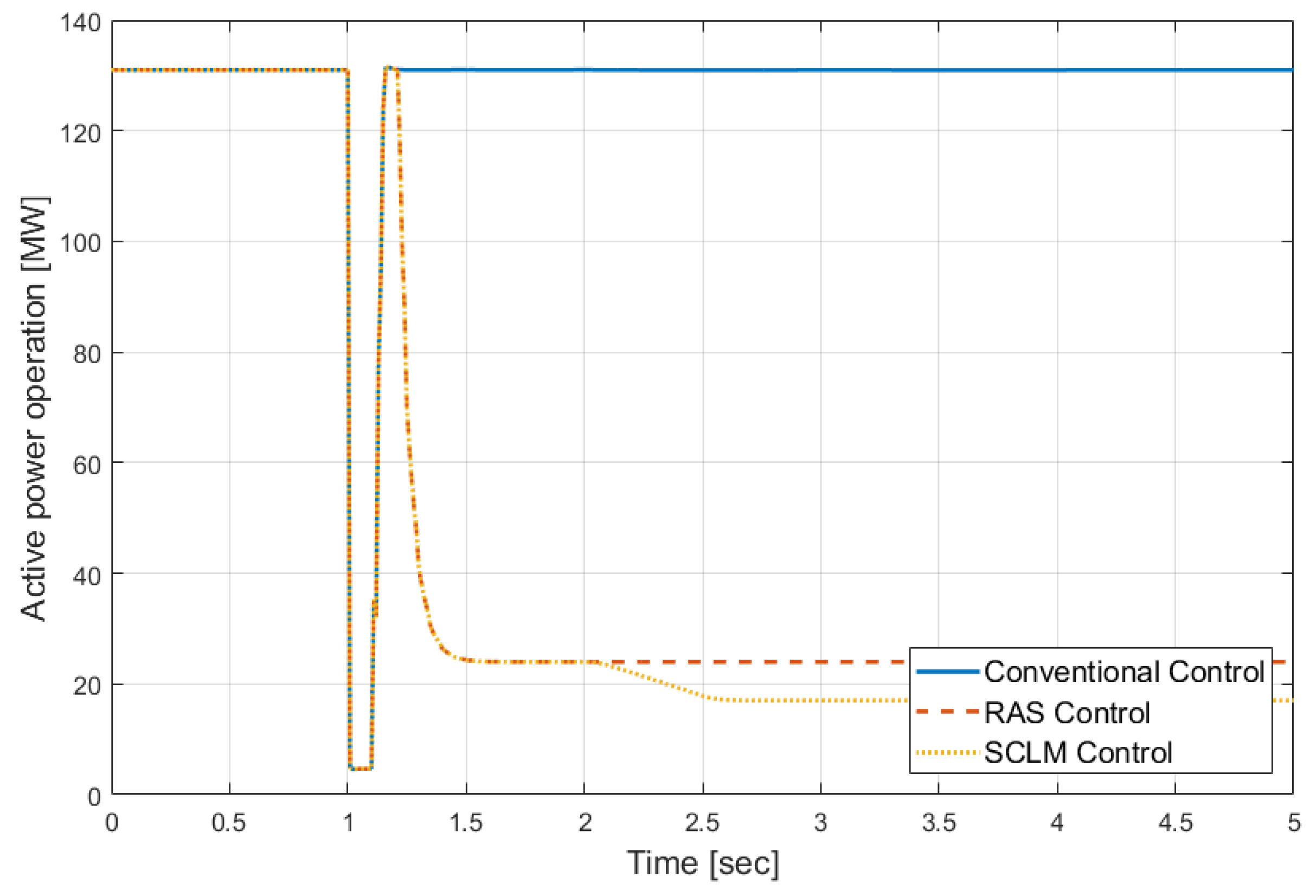
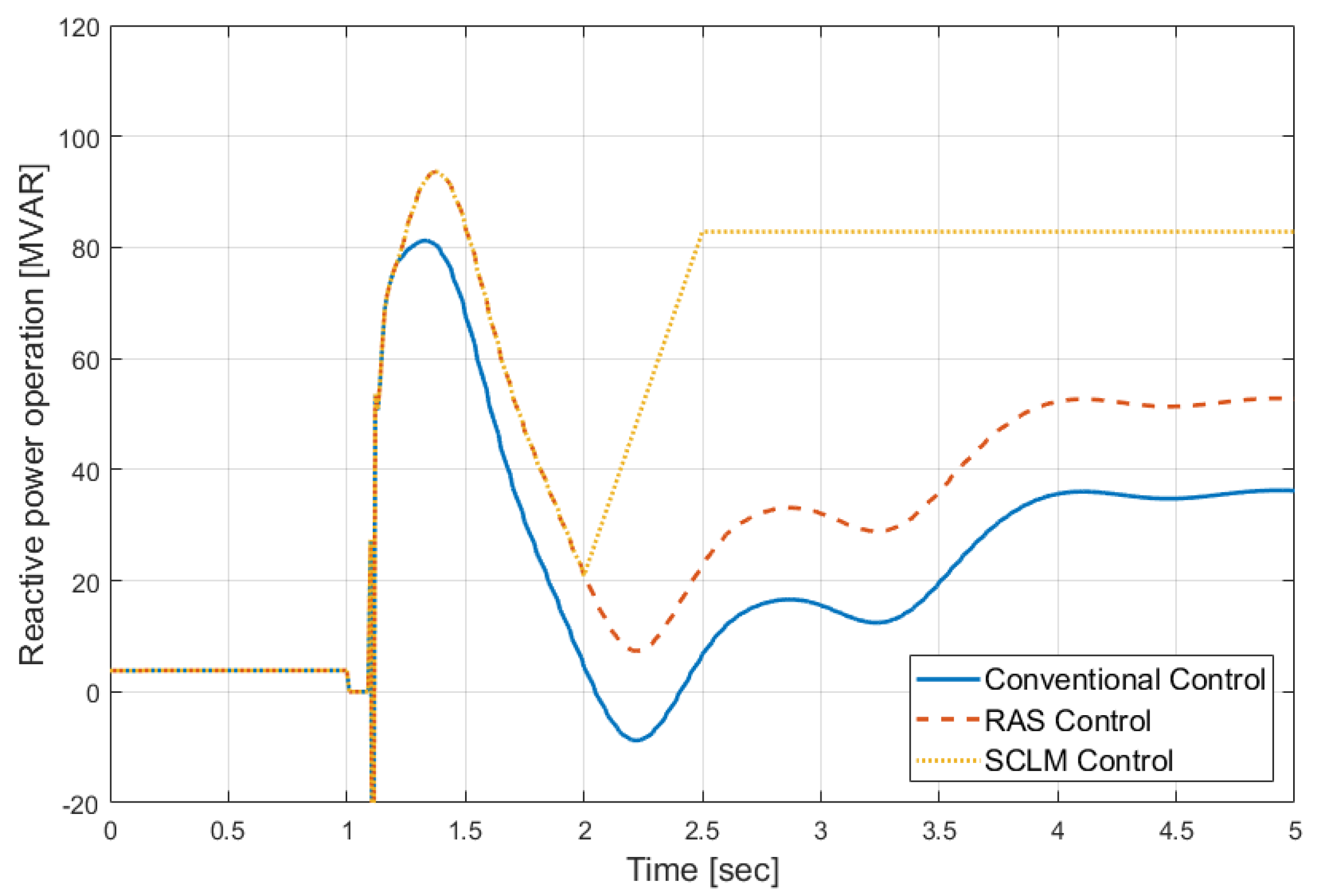
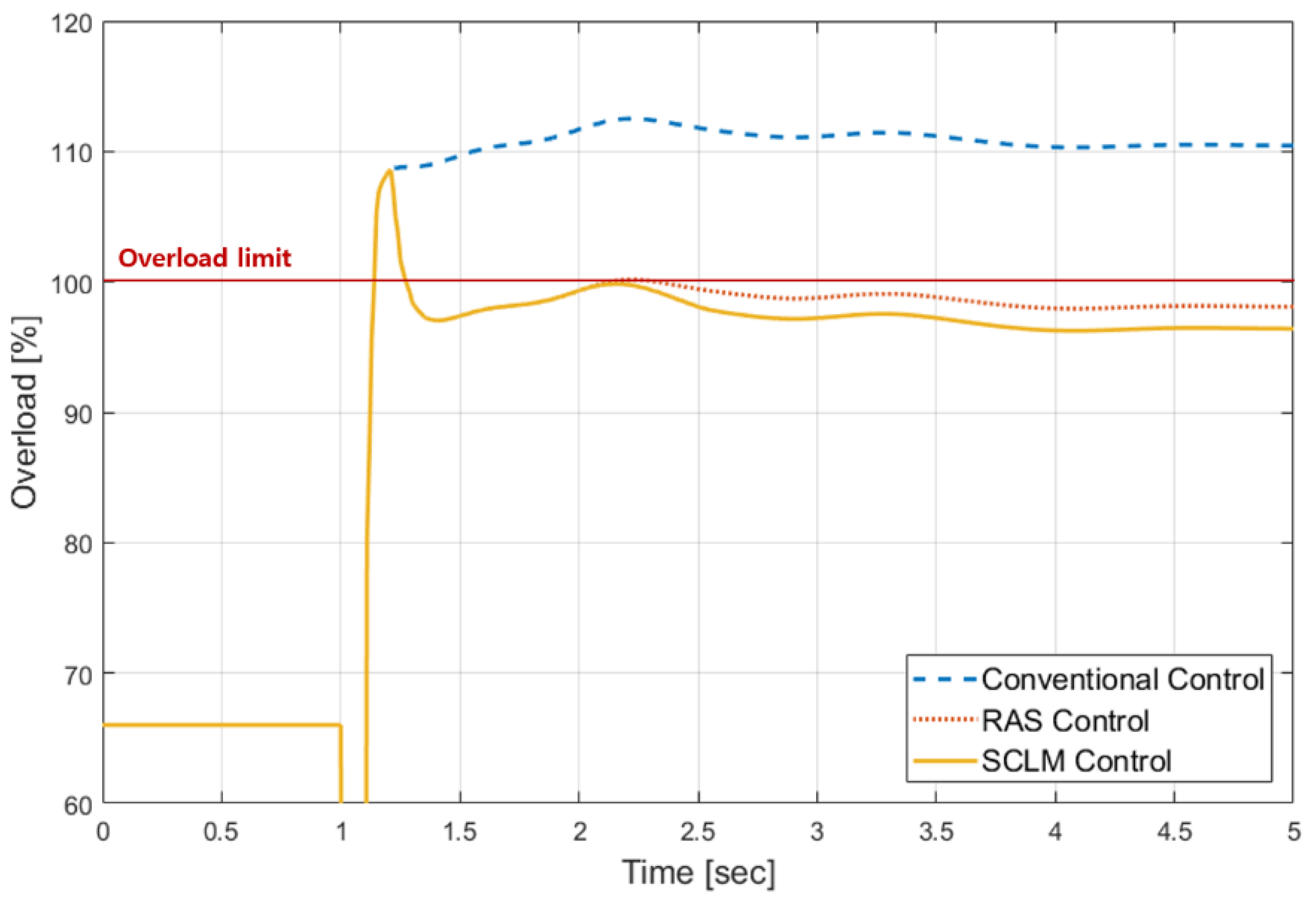
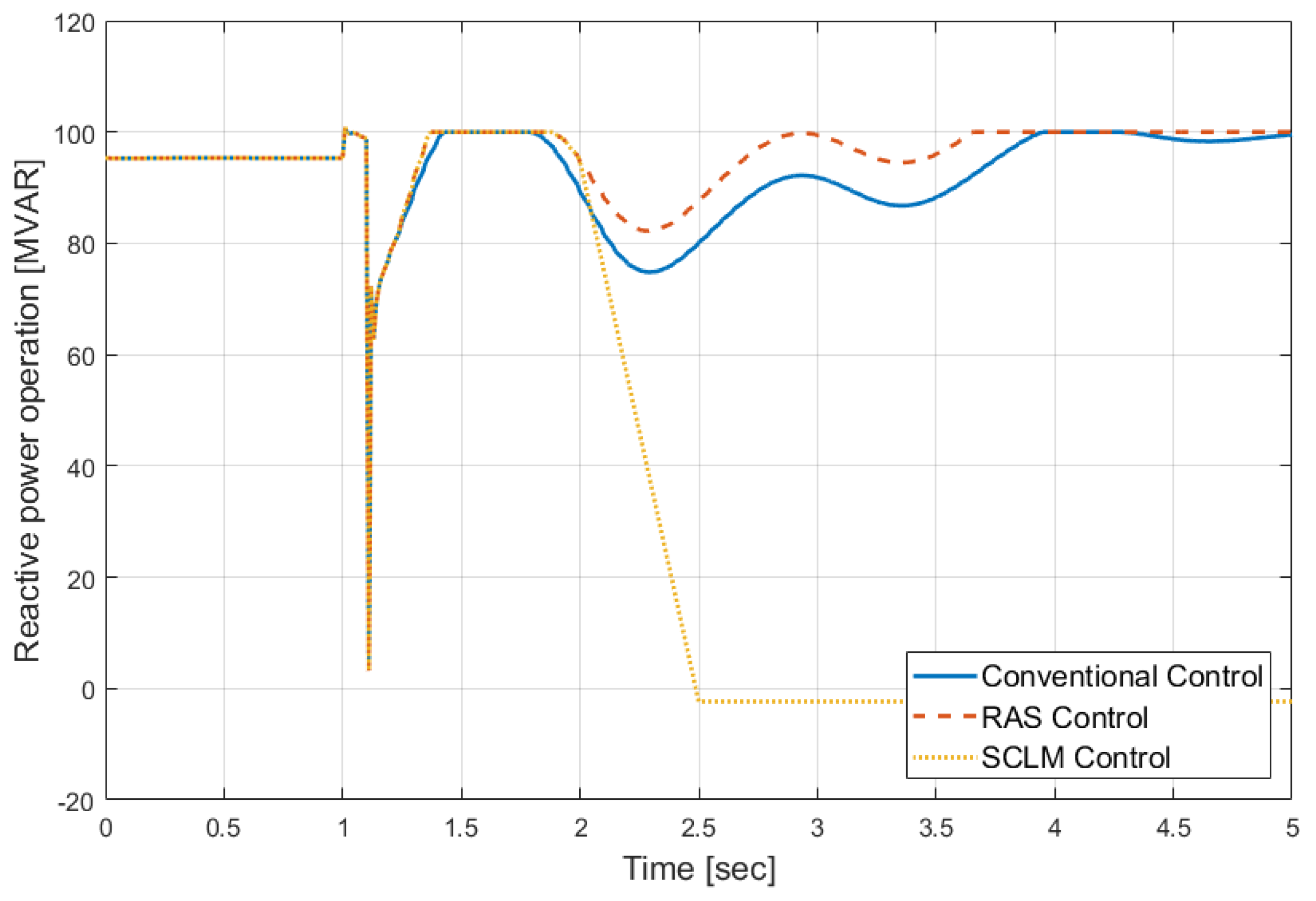
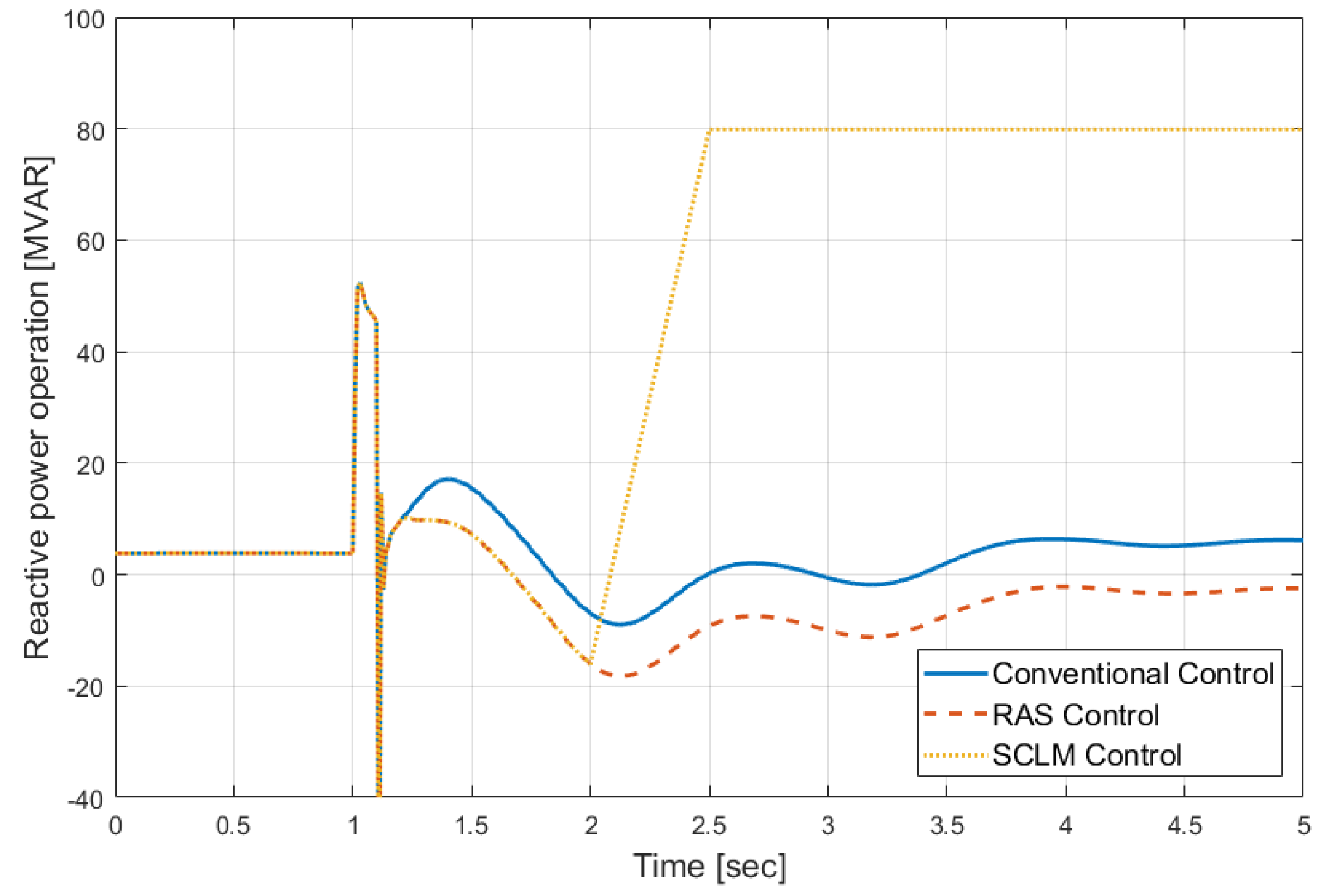
4.4.1. Transformer Overload (100%) Case
4.4.2. Line Overload (120%) Case
4.4.3. Comparison of Simulation Results
5. Conclusions
- In normal operation, the system loss is reduced by about 16 MW in the STLM control. This is 1% of the total loss, but an economic benefit can be gained during the lifetime of HVDC. Although we did not perform a detailed economic assessment, it is possible to obtain a loss reduction effect of about 85 million dollars a year considering energy charge and demand charge.
- There are about 180 branches in the zone with HVDC. Using sensitivity analysis, the number of monitoring branches can be reduced to 14 lines and three transformers.
- If a disturbance occurs in the AC system and there is no appropriate HVDC control accordingly, HVDC may adversely affect the AC system. Using the SCLM control, not only overload and overvoltage problems are solved, but also the system loss is reduced, which is advantageous in economy and reliability.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| 1310–1340 | 1340–1825 | 1360–1945 | 1361–1945 | 1411–1495 | 1411–1925 |
| 1495–1690 | 1690–1945 | 1825–1890 | 1865–1870 | 1890–1935 | 1925–1931 |
| 1931–1940 | 1935–1940 | 1360 M.Tr | 1361 M.Tr | 1410 M.Tr |
References
- Van Hertem, D.; Ghandhari, M. Multi-terminal VSC HVDC for the European supergrid: Obstacles. Renew. Sustain. Energy Rev. 2010, 14, 3156–3163. [Google Scholar] [CrossRef]
- Van Hertem, D.; Gomis-Bellmunt, O.; Liang, J. HVDC Grids: For Offshore and Supergrid of the Future; John Wiley & Sons: Hoboken, NJ, USA, 2016; ISBN 9781118859155. [Google Scholar]
- Peake, O. The history of high voltage direct current transmission. Aust. J. Multi Discip. Eng. 2010, 8, 47–55. [Google Scholar] [CrossRef]
- Renner, R.H.; Van Hertem, D. Ancillary services in electric power systems with HVDC grids. IET Gener. Transm. Distrib. 2015, 9, 1179–1185. [Google Scholar] [CrossRef]
- Henry, S.; Despouys, O.; Adapa, R.; Barthold, C.; Bell, K.; Binard, J.-L.; Edris, A.; Egrot, P.; Hung, W.; Irwin, G.; et al. Influence of embedded HVDC transmission on system security and AC network performance. Electra 2013, 267, 79–86. [Google Scholar]
- Johnson, R.K.; Klemm, N.S.; De Laneuville, H.; Koetschau, S.G.; Wild, G. Power modulation of Sidney HVDC scheme. I. RAS control concept, realization and field tests. IEEE Trans. Power Deliv. 1989, 4, 2145–2152. [Google Scholar] [CrossRef]
- Johnson, R.K.; Klemm, N.S.; Schiling, K.H.; Thumm, G. Power modulation of Sidney HVDC scheme. II. Computer simulation. IEEE Trans. Power Deliv. 1989, 4, 2153–2161. [Google Scholar] [CrossRef]
- Lee, R.L.; Melvold, D.J.; Szumlas, D.J.; Le, L.M.; Finley, A.T.; Martin, D.E.; Wong, W.K.; Dickmander, D.L. Potential DC system support to enhance AC system performance in the Western United States. IEEE Trans. Power Syst. 1993, 8, 264–274. [Google Scholar] [CrossRef]
- Cholley, P.; Crossley, P.; Van Acker, V.; Van Cutsem, T.; Fu, W.; Soto Idia Òez, J.; Ilar, F.; Karlsson, D.; Kojima, Y.; McCalley, J.; et al. System protection schemes in power networks. In Proceedings of the 2001 Seventh International Conference on Developments in Power System Protection (IEE), Amsterdam, The Netherlands, 2001; pp. 450–453. [Google Scholar]
- Luo, J.; Gong, Y.; Li, H.; Yan, Y. Online emergency control and corrective control coordination strategy for UHVDC blocking faults. In Proceedings of the 2018 IEEE International Conference on Electronics Technology (ICET 2018), Chendu, China, 23–27 May 2018; pp. 5–10. [Google Scholar]
- Jiang, M.; Yu, H. Alberta’s experience of coordinating HVDC operation with under-voltage remedial action scheme. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM 2016), Boston, MA, USA, 17–21 July 2016; pp. 1–4. [Google Scholar]
- Bhuiyan, M.R.; Taylor, A.E.; Kezman, N.C. Designing the hardware and software of the Pacific HVDC intertie remedial action scheme using a programmable controller. In Proceedings of the 1991 IEEE Power Engineering Society Transmission and Distribution Conference, Dallas, TX, USA, 22–27 September 1991; pp. 790–796. [Google Scholar]
- Dolezilek, D. Case study examples of interoperable ethernet communications within distribution, transmission, and wide-area control systems. In Proceedings of the 2010 IEEE International Conference on Communications Workshops (ICC 2010), Cape Town, South Africa, 23–27 May 2010; pp. 1–7. [Google Scholar]
- Bahrman, M.; Bjorklund, P.-E. The new black start: System restoration with help from voltage-sourced converters. IEEE Power Energy Mag. 2014, 12, 44–53. [Google Scholar] [CrossRef]
- Yoon, M.; Yoon, Y.-T.; Jang, G. A study on maximum wind power penetration limit in island power system considering high-voltage direct current interconnections. Energies 2015, 8, 14244–14259. [Google Scholar] [CrossRef]
- Miao, Y.; Cheng, H. An optimal reactive power control strategy for UHVAC/DC hybrid system in east china grid. IEEE Trans. Smart Grid 2016, 7, 392–399. [Google Scholar] [CrossRef]
- Moslehi, K. Electricity market challenges—Efficient utilization of transmission. In Proceedings of the 2015 IEEE Smart Grids Seminar, Cuernavaca, Morelos, Mexico, 23–27 March 2015. [Google Scholar]
- Cao, J.; Du, W.; Wang, H.F.; Bu, S.Q. Minimization of transmission loss in meshed AC/DC grids with VSC-MTDC networks. IEEE Trans. Power Syst. 2013, 28, 3047–3055. [Google Scholar] [CrossRef]
- Han, M.; Xu, D.; Wan, L. Hierarchical optimal power flow control for loss minimization in hybrid multi-terminal HVDC transmission system. CSEE J. Power Energy Syst. 2016, 2, 40–46. [Google Scholar] [CrossRef]
- QI, Q.; Long, C.; Wu, J.; Yu, J. Impacts of a medium voltage direct current link on the performance of electrical distribution networks. Appl. Energy 2018, 230, 175–188. [Google Scholar] [CrossRef]
- QI, Q.; Wu, J.; Long, C. Multi-objective operation optimization of an electrical distribution network with soft open point. Appl. Energy 2017, 208, 734–744. [Google Scholar] [CrossRef]
- Vovos, P.N.; Song, H.; Cho, K.-V.; Kim, T.-S. A network reconfiguration algorithm for the reduction of expected fault currents. In Proceedings of the 2013 IEEE Power and Energy Society General Meeting (PES 2013), Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Lee, J.-H.; Yoon, M.; Jung, S.; Jang, G. System reliability enhancement in a metropolitan area using HVDC technology. J. Int. Counc. Electr. Eng. 2015, 5, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Tongsiri, S.; Hoonchareon, N. Fault current limitation in metropolitan power system using HVDC link. In Proceedings of the 8th IEEE Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON 2011), Khon Kaen, Thailand, 17–20 May 2011; pp. 840–844. [Google Scholar]
- Pang, H.; Tang, G.; He, Z. Evaluation of losses in VSC-HVDC transmission system. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–6. [Google Scholar]
- Sellick, R.L.; Åkerberg, M. Comparison of HVDC light (VSC) and HVDC classic (LCC) site aspects, for a 500 MW 400 kV HVDC transmission scheme. In Proceedings of the 10th IET International Conference on AC and DC Power Transmission (ACDC 2012), Birmingham, UK, 4–5 December 2012. [Google Scholar]
- Fradi, A.; Brignone, S.; Wollenberg, B.E. Calculation of energy transaction allocation factors. IEEE Trans. Power Syst. 2001, 16, 266–272. [Google Scholar] [CrossRef]
- Song, C.S.; Park, C.H.; Yoon, M.; Jang, G. Implementation of PTDFs and LODFs for power system security. J. Int. Counc. Electr. Eng. 2011, 1, 49–53. [Google Scholar] [CrossRef]
- Rahmani, M.; Kargarian, A.; Hug, G. Comprehensive power transfer distribution factor model for large-scale transmission expansion planning. IET Gener. Transm. Distrib. 2016, 10, 2981–2989. [Google Scholar] [CrossRef]
- Powell, M.J.D. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964, 7, 155–162. [Google Scholar] [CrossRef]
- Lazarou, S.; Vita, V.; Ekonomou, L. Application of powell’s optimisation method for the optimal number of wind turbines in a wind farm. IET Sci. Meas. Technol. 2011, 5, 77–80. [Google Scholar] [CrossRef]
- Cao, W.; Wu, J.; Jenkins, N. Feeder load balancing in MV distribution networks using soft normally-open points. In Proceedings of the 2014 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe 2014), Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- Asplund, G.; Eriksspon, K.; Jiang, H.; Lindberg, J.; Pålsson, R.; Swensson, K. DC transmission based on voltage source converters. In CIGRE SC14 Colloquium, South Africa; ABB Power Systems AB: Vasteras, Sweden, 1997; pp. 1–7. [Google Scholar]
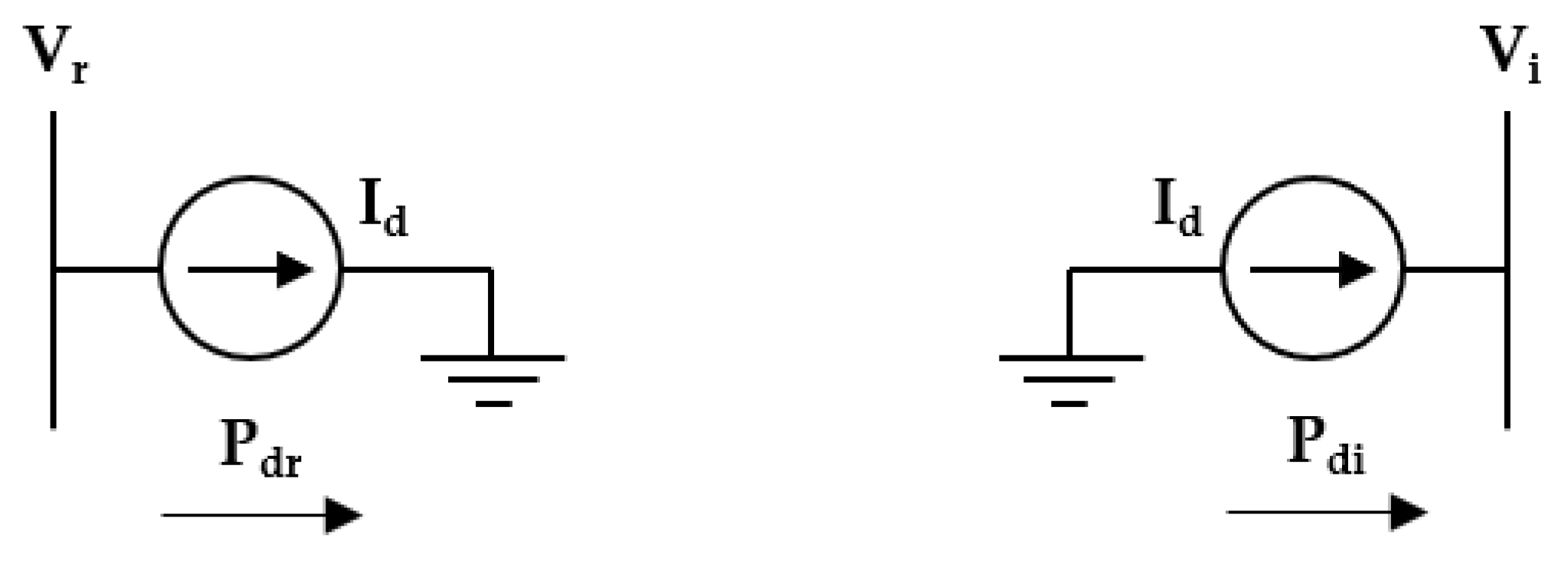





| Control and Support | Grid Service |
|---|---|
| Active power control and frequency support | - Primary control or frequency containment reserves (FCR) |
| - Secondary control or frequency restoration reserves (FRR) | |
| - Tertiary control or replacement reserves (RR) | |
| Reactive power control and voltage support | - Reactive power absorb/supply |
| Rotor angle stability-related control | - Avoiding loss of synchronism |
| - Damping electromechanical oscillations | |
| Other | - Power oscillation damping capability |
| - DC power flow control | |
| - Black start capability | |
| - Loss compensation | |
| - DC transmission reserve |
| Item | Information | |
|---|---|---|
| Case data | Korea Power System (2021) | |
| System total generation | 98,771.0 MW | |
| System total load | 97,200.8 MW | |
| Nominal frequency | 60 Hz | |
| Voltage limit (Steady state) | Base 345 kV | 0.95~1.05 p.u. |
| Base 154 kV | 0.90~1.10 p.u. | |
| Voltage limit (Transient state) | Base 345 kV | 0.90~1.05 p.u. |
| Base 154 kV | 0.90~1.10 p.u. | |
| Branch Overload limit (Steady state) | Branch | 100% |
| Branch Overload limit (Transient) | Line | 120% |
| Transformer | 100% | |
| Specification | BTB VSC HVDC |
|---|---|
| Site | 1410–1411 |
| Active power capacity | 200 × 2 MW |
| Reactive power capacity | 100 × 2 MVAR |
| MVA rating | 224 × 2 MVA |
| AC terminal voltage | 154 kV |
| DC voltage | 100 kV |
| Configuration | Double monopole |
| Conversion loss | 1.8% of active power |
| AC voltage setpoint | Depend on the system condition |
| Bus Number | Base kV | With HVDC | Without HVDC | Bus Number | Base kV | With HVDC | Without HVDC |
|---|---|---|---|---|---|---|---|
| 1200 | 345 | 54.8899 | 55.0129 | 1810 | 154 | 48.2441 | 53.2228 |
| 1400 | 345 | 48.2340 | 50.1957 | 1811 | 154 | 47.7596 | 52.6257 |
| 1410 | 154 | 49.7672 | 65.5842 | 1865 | 154 | 46.2224 | 51.5447 |
| 1411 | 154 | 25.7956 | 65.5842 | 1870 | 154 | 47.0455 | 52.7775 |
| 1475 | 154 | 46.1315 | 51.8724 | 1895 | 154 | 47.1782 | 53.1212 |
| 1490 | 154 | 46.2564 | 52.0078 | 1955 | 154 | 44.5498 | 50.1641 |
| P (1410 → 1411) | AC Voltage (Rectifier) | AC Voltage (Inverter) | |
|---|---|---|---|
| Setpoint | 131 × 2 MW | 1.048 kV | 1.039 kV |
| (Supply 95.31 MVAR) | (Supply 3.80 MVAR) |
| Losses | With HVDC (STLM Control) | With HVDC (AC Flow) | Without HVDC |
|---|---|---|---|
| AC system losses | 1564.38 MW | 1578.10 MW | 1571.16 MW |
| DC system losses | 4.72 MW | 7.20 MW | - |
| Total losses | 1569.10 MW | 1585.30 MW | 1571.16 MW |
| Control Mode | P (1410 → 1411) | AC Voltage (Rectifier) | AC Voltage (Inverter) |
|---|---|---|---|
| Normal operation (STLM control) | 131 × 2 MW | 1.048 kV | 1.039 kV |
| (Supply 95.31 MVAR) | (Supply 3.80 MVAR) | ||
| SCLM control | 17 × 2 MW | 1.019 kV | 1.048 kV |
| (Supply 82.83 MVAR) | (Supply 72.70 MVAR) |
| Normal Operation | Conventional Control | RAS Control | SCLM Control | |
|---|---|---|---|---|
| AC system losses | 1564.38 MW | 1583.92 MW | 1587.21 MW | 1585.80 MW |
| DC system losses | 4.72 MW | 4.72 MW | 0.86 MW | 0.61 MW |
| Total losses | 1569.10 MW | 1587.64 MW | 1588.07 MW | 1586.41 MW |
| % Loading | 66.02% | 110.44% (Security violated) | 98.08% | 96.41% |
| Control Mode | P (1410→1411) | AC Voltage (Rectifier) | AC Voltage (Inverter) |
|---|---|---|---|
| Normal operation (STLM control) | 131 × 2 MW | 1.048 kV | 1.039 kV |
| (Supply 95.31 MVAR) | (Supply 3.80 MVAR) | ||
| SCLM control | 184 × 2 MW | 1.035 kV | 1.042 kV |
| (Absorb 2.34 MVAR) | (Supply 79.86 MVAR) |
| Normal Operation | Conventional Control | RAS Control | SCLM Control | |
|---|---|---|---|---|
| AC system losses | 1564.38 MW | 1575.28 MW | 1573.28 MW | 1568.02 MW |
| DC system losses | 4.72 MW | 4.72 MW | 7.20 MW | 6.62 MW |
| Total losses | 1569.10 MW | 1580.00 MW | 1580.48 MW | 1574.64 MW |
| % Loading | 62.98% | 122.27% (Security violated) | 116.17% | 119.08% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Yoon, M.; Hwang, S.; Jeong, S.; Jung, S.; Jang, G. Development of A Loss Minimization Based Operation Strategy for Embedded BTB VSC HVDC. Appl. Sci. 2019, 9, 2234. https://doi.org/10.3390/app9112234
Lee J, Yoon M, Hwang S, Jeong S, Jung S, Jang G. Development of A Loss Minimization Based Operation Strategy for Embedded BTB VSC HVDC. Applied Sciences. 2019; 9(11):2234. https://doi.org/10.3390/app9112234
Chicago/Turabian StyleLee, Jaehyeong, Minhan Yoon, Sungchul Hwang, Soseul Jeong, Seungmin Jung, and Gilsoo Jang. 2019. "Development of A Loss Minimization Based Operation Strategy for Embedded BTB VSC HVDC" Applied Sciences 9, no. 11: 2234. https://doi.org/10.3390/app9112234
APA StyleLee, J., Yoon, M., Hwang, S., Jeong, S., Jung, S., & Jang, G. (2019). Development of A Loss Minimization Based Operation Strategy for Embedded BTB VSC HVDC. Applied Sciences, 9(11), 2234. https://doi.org/10.3390/app9112234









