Automatic Detection and Staging of Lung Tumors using Locational Features and Double-Staged Classifications

Abstract

Lung cancer is a life-threatening disease with the highest morbidity and mortality rates of any cancer worldwide. Clinical staging of lung cancer can significantly reduce the mortality rate, because effective treatment options strongly depend on the specific stage of cancer. Unfortunately, manual staging remains a challenge due to the intensive effort required. This paper presents a computer-aided diagnosis (CAD) method for detecting and staging lung cancer from computed tomography (CT) images. This CAD works in three fundamental phases: segmentation, detection, and staging. In the first phase, lung anatomical structures from the input tomography scans are segmented using gray-level thresholding. In the second, the tumor nodules inside the lungs are detected using some extracted features from the segmented tumor candidates. In the last phase, the clinical stages of the detected tumors are defined by extracting locational features. For accurate and robust predictions, our CAD applies a double-staged classification: the first is for the detection of tumors and the second is for staging. In both classification stages, five alternative classifiers, namely the Decision Tree (DT), K-nearest neighbor (KNN), Support Vector Machine (SVM), Ensemble Tree (ET), and Back Propagation Neural Network (BPNN), are applied and compared to ensure high classification performance. The average accuracy levels of 92.8% for detection and 90.6% for staging are achieved using BPNN. Experimental findings reveal that the proposed CAD method provides preferable results compared to previous methods; thus, it is applicable as a clinical diagnostic tool for lung cancer.

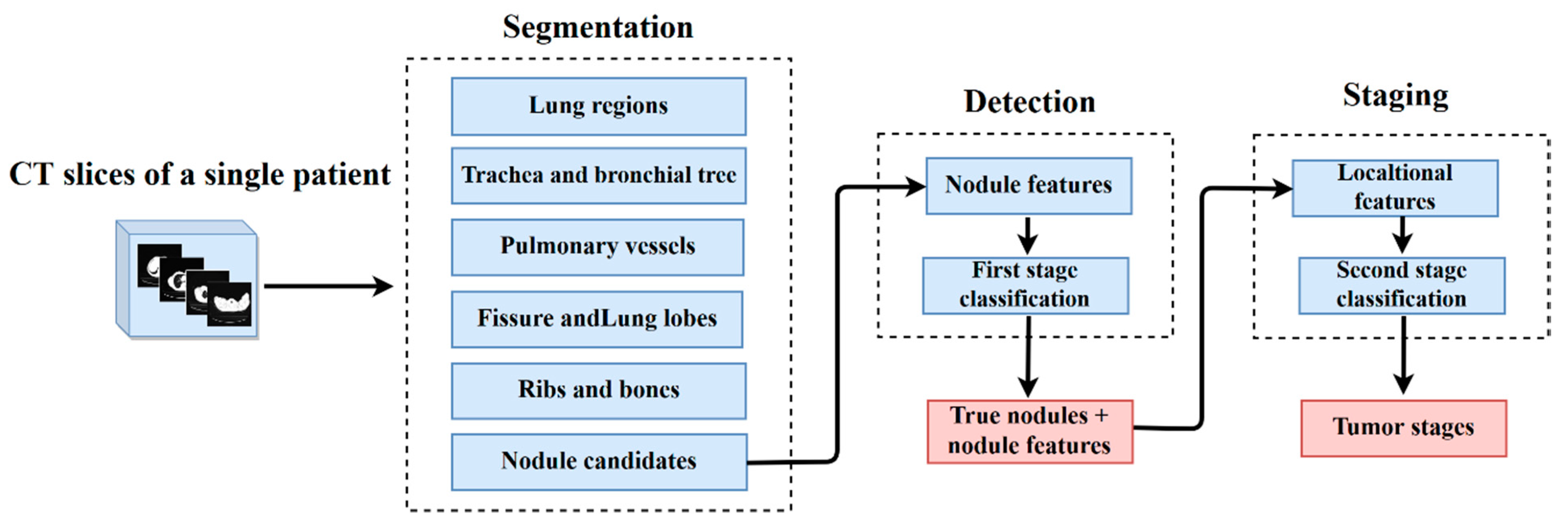
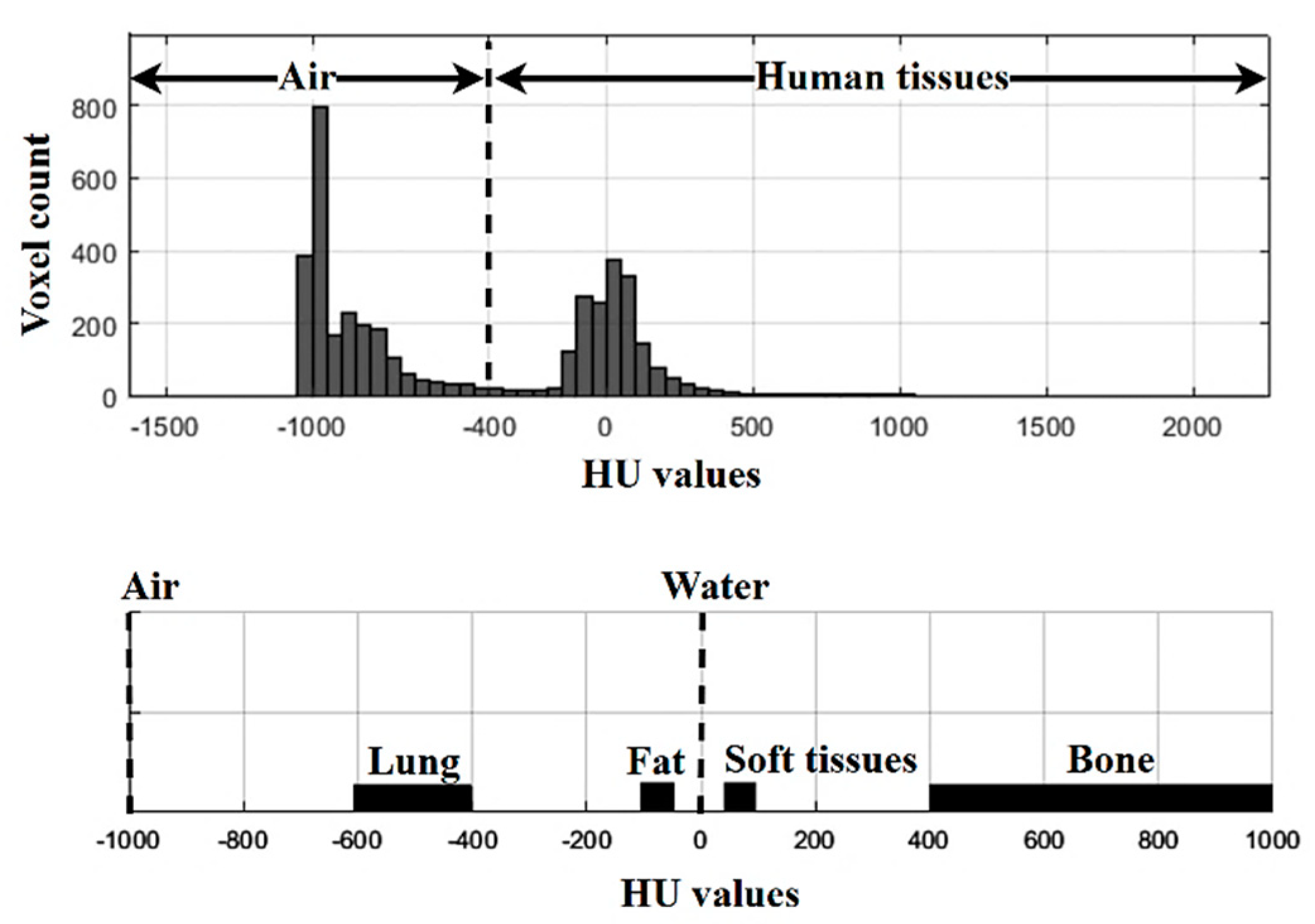
1. Introduction

Lung cancer is one of the most common diseases, and it has the highest morbidity and mortality rates of any cancer worldwide. As reported by global cancer statistics [1], there were 2.1 million new cases and 1.8 million deaths from lung cancer in 2018. Approximately one in five cases (18.4%) of lung cancer leads to death. In oncology, medical imaging plays a vital role in reducing the mortality rate. Imaging is a non-invasive and painless procedure with the least harmful side effects for patients. It can provide detailed anatomical information about the disease by generating visual representations of tumors. Unlike other invasive methods such as surgeries and biopsies which extract and study a small portion of tumor tissue, imaging can give a more comprehensive view and analysis of the entire tumor region. Moreover, it is preferable for clinical routines that require an iterative analysis of the tumor during treatment [2].

Computed tomography (CT) is a standard imaging modality for lung cancer diagnosis. The National Lung Screening Trial (NLST) reported that the lung cancer mortality rate of 15–20% could be reduced by performing low-dose CT screening [3]. CTs display tumors on cross-sectional images of the body called “slices”. These slices can be stacked together to reconstruct a three-dimensional structure which makes possible more comprehensive analysis of tumors. However, the manual interpretation of the CT scans is prohibitively expensive in terms of time and effort. Also, it is subject to the skill and clinical practices of the interpreter; hence, the diagnosis results may suffer from inter- and intra-observer variation [4]. Due to these inconveniences, any real-world application is necessary for automated interpretations of the CT scans. This fact has strongly motivated computer-aided diagnosis systems (CADs) to become an extensive research area in the field of biomedical engineering. Scientists have proposed a vast number of CADs for lung cancer diagnosis using modern image processing and machine learning techniques. Nonetheless, most of these CADs have focused only on the detection of pulmonary nodules. Nodules can evoke the possibility of lung cancer and appear as round or oval-shaped opacities on the CT scans [5]. Nonetheless, the detection of nodules does not provide sufficient information about the severity of the disease to make proper treatment decisions. Generally, half of the patients who undergo CT screening present more than one nodule, but not all of these nodules are cancerous [6]. Physicians usually use the terms “nodule” and “tumor” interchangeably when they are uncertain about the severity of the disease. Indeed, identifying the severity of a tumor nodule is a principal issue for lung cancer diagnosis.

In clinical practice, the severity of lung cancer can be expressed as different stages using the Tumor, Node, and Metastasis (TNM) system [7]. As the name describes, this system assesses the severity of the disease based on three descriptors. The first descriptor (T) assesses the characteristics of the primary tumor such as its size, local invasion, and the presence of satellite tumor nodules. The CT modality performs T-staging well, because information about the tumor can be easily obtained from the CT scans. The second descriptor (N) assesses the involvement of the regional lymph nodes. On the CT scans, lymph nodes appear as small opacities with unclear silhouettes; thus, the CT modality performs weakly for N-staging [8,9]. The last descriptor (M) assesses the invasion of the tumor to the extra-thoracic organs, especially the brain, adrenal glands, liver and bones, and so forth [9]. Staging of metastatic tumors usually requires additional examinations of the invaded body regions. For this reason, we focus only on the T-staging of tumor nodules in this study. T-stages can be further divided into sub-stages depending on the anatomic characteristics of the primary tumors.

Table 1. T-staging of lung tumors.

Stages		Sizes (in Greatest Dimension)	Invasion
Tx		Tumor cannot be assessed
T0		No evidence of primary tumor
Tis		Carcinoma in situ (pre-cancer)
T1		≤3 cm	Surrounded by lung or visceral pleura. Invades the lobar bronchus but not the main bronchus.
	T1a	≤2 cm
	T1b	>2 cm and ≤3 cm
T2		>3 cm and ≤5 cm	Invades the main bronchus, regardless of distance from the carina but does not invade the carina. Invades the visceral pleura. Invades the hilar region.
	T2a	>3 cm and ≤4 cm
	T2b	>4 cm and ≤5 cm
T3		>5 cm and ≤7 cm	Invades the chest wall, phrenic nerve, and parietal pericardium. Presents satellite nodules in the same lobe.
T4		>7 cm	Invades the diaphragm, mediastinum, heart, great vessels, and trachea. Presents satellite nodules in the different lobes.

describes the detailed definitions of the T-stages, as determined by the eighth edition of the TNM system.

2. Related Works

The remaining problem of existing lung cancer diagnosis systems is that they are capable of detecting tumor nodules only. As there are numerous nodule-like lesions in the lungs, it is still challenging to detect real tumor nodules. Most current CADs thus try to reduce the number of false positives, which can hinder the detection of real nodules. This means that current CADs defer staging assessments. Even though there have been a lot of studies on the computerized detection of tumor nodules, we found a paucity of literature on staging. In 2014, Kulkarni and Panditrao [10] proposed an automatic tumor staging system from chest CT scans using marker-controlled watershed and Support Vector Machine (SVM). As a pre-processing method, they smoothed the input CT images with a Gabor filter, and then possible tumor nodules from the smoothed CT slices were segmented using marker-controlled watershed. Next, three geometric features—area, perimeter and eccentricity—were extracted and fed into the Support Vector Machine (SVM) for classification. Their method produced diagnosis results in four stages (T1, T2, T3, and T4), and they evaluated 40 CT scans from the National Institute of Health/ National Cancer Institute (NIH/NCI) Lung Image Database Consortium (LIDC) dataset. However, the evaluation assessments were not described in detail.

Similarly, Ignatious et al. (2015) [11] applied marker-controlled watershed for lung tumor detection and staging. Unlike [10], they used the sharpening method to enhance the input CT slices and then five features—area, perimeter, eccentricity, convex area and mean intensity—were extracted. They selected the true tumors based on an empirical threshold value of area. After that, staging was conducted by four alternative classifiers: Support Vector Machine (SVM), Naive Bayes Multinomial classifier (NBM), Naive Bayes Tree (NB tree), and Random Tree. Their experiment was validated using 200 CT slices from Regional Cancer Centre Trivandrum, and an accuracy level of 94.4% was obtained by the Random Tree classifier. Nevertheless, tumor segmentation based on the marker-controlled watershed is hard to fully automate, and it has a low guarantee in detecting any shape and size of nodules, because creating internal and external markers for affine variant nodules is an arduous task.

Besides the aforementioned CADs, a multi-stage cancer detection method using watershed and multi-class SVM classifier was also proposed by Alam et al. (2018) [12]. In their study, the median filter was used for the pre-processing of 500 lung CT images, and then thirteen different image features were extracted from the region of interest (ROI). In the first stage of classification, they try to detect any cancerous tumor nodules from the input CT exam. If there were cancerous tumors, they identified the clinical stages of those tumors in the second stage of classification. Otherwise, they calculated the probability of non-cancerous tumors becoming cancer in the third stage. For the first and second stages, they used the SVM classifier, and for the third stage, they calculated the area ratio (area of the nodule to the area of the entire lung). Their experiment reached accuracy levels of 97% for detection and 87% for staging, respectively. Our proposed CAD which applies two stages of classification for detection and staging is quite similar to that presented in [12]. However, we differ from them by extracting the locational features of cancerous tumors and using alternative machine learning algorithms for classification. Moreover, we determine the clinical stages of tumors using the eighth edition of the TNM staging method, which is a global, up-to-date standard for cancer staging. In their approach, they classified the stages (initial, middle, and final) roughly; thus, it was not very beneficial for precise treatment.

Recently, deep learning models have made great breakthroughs for machine learning [13]. Convolutional Neural Networks (CNNs) are the most frequently used deep learning model for the automated detection of lung tumors. However, for staging, CNN has been applied in very few studies. Kirienko et al. (2018) [14] developed a CNN for T1–T2 or T3–T4 staging of lung tumors. Their staging referenced the seventh edition of the TNM system and tested with 472 FDG-PET/CT scans. Their proposed CNN was constructed using 2D patches that were cropped around the center of the tumor. Additionally, their CNN used two neural networks: (i) one as a feature extractor to extract the most relevant features from a single patch, and (ii) another as a classifier to perform classifications for all slices. They reported a high testing accuracy of 90%, but the outputs were presented as binary numbers (T1–T2 with label = 0 and T3–T4 with label = 1), that is, their method cannot give an accurate result for each specific stage. Moreover, their approach is not fully automated, because their CNN requires manually cropped patches as inputs.

Another tumor staging method using a double convolutional deep neural network (CDNN) was presented in [15]. They used 73 CT exams from the Image and Data Archive of the University of South Carolina and the Laboratory of Neuro Imaging (LONI) dataset. They divided the input exams into two piles: pile 1 (with cancer) and pile 2 (without cancer). Then, all slices in both piles were further grouped depending on the angles using the K-means algorithm. Subsequently, they built a double CDNN containing double convolution layers and an additional max pooling layer. They reported a prediction accuracy of 99.62%. Nonetheless, their CDNN output only decimal values between 0 (non-cancer) and 1 (cancer); hence, a threshold value was necessary to determine the possibility of tumor stages.

The primary objective of this paper is to propose a CAD that is capable of not only the detection of tumor nodules, but also of their staging. We present two significant contributions in our work; the first is performing double-staged classification, and the second is the extraction of locational features. In the first contribution, we perform two stages of classifications: one for the detection task and another for the staging task. Performing double-staged classification helps to minimize false positives and makes the CAD more accurate and robust. In the second contribution, we extract the locational features to identify the stages of the lung tumor because the severity of lung cancer strongly depends on the sizes and locations of the tumor nodules. Moreover, knowing the exact locations of tumor nodules is implicitly beneficial for the surgical planning of higher staged tumors. The rest of this paper is organized as follow. Section 3 describes the details of the methods applied in this study. Section 4 presents the experimental results and performance evaluation of the proposed method. Finally, Section 5 presents the discussion and conclusions of the paper.

3. Methods

This section presents the details of the procedures and algorithms applied in our proposed CAD. Figure 1 outlines the typical architecture of the proposed CAD which operates in three fundamental phases: (i) segmentation of the lung anatomical structures, (ii) detection of true tumor nodules, and (iii) staging of tumor nodules.

3.1. Segmentation of the Lung Anatomical Structures

Segmentation of the lung anatomical structures from the input CT scans needs to be performed as an initial task. This helps detection faster and easier by eliminating unwanted non-body areas from the input image, for examples, exam sheets, tables, and so on. Moreover, it is crucial for the extraction of information in the subsequent analysis of tumor stages. For accurate segmentation of the lung structures, background anatomy knowledge is indispensable. Hence, before segmentation, we briefly study the anatomical structures of the lungs and their appearance on the CT scan (Section 3.1.1). Based on this anatomical knowledge, the segmentation is conducted using two basic algorithms: gray-level thresholding (Section 3.1.2) and isotropic interpolation (Section 3.1.3). However, depending on the structure that we want to segment, some methods may be different. Thus, the details of the segmentation methods for each lung structure are described in Section 3.1.4, Section 3.1.5, Section 3.1.6, Section 3.1.7, Section 3.1.8 and Section 3.1.9. Regarding the proper localization of lung tumors relative to the surrounding anatomical structures, these segmentations will make the locational feature extraction process more convenient.

3.1.1. Lung Anatomical Structures

As depicted in the schematic diagram of lung structures in Figure 2a, there are two major organs: the left and the right lung. Each is enclosed by a pleural sac with two membranes called visceral pleura (inner membrane highlighted by the black border) and parietal pleura (outer membrane highlighted by the blue border). These membranes protect and attach the lungs to the thoracic cavity. A double-fold of visceral pleura called the lung fissure divides the lungs into separate lobes. The left lung is approximately 10% smaller than the right due to heart space in the thorax [16]. Thus, the left lung has only two lobes (upper and lower) which are separated by an oblique fissure, while the right lung has three lobes (upper, middle and lower) which are separated by oblique and horizontal fissures. As the primary function of the lungs is to carry out gas exchange, 80–90% of their area is filled with low density air having −1000 Hounsfield Unit (HU) [17]. The windpipe, also known as the trachea (denoted by green color), carries the air from the throat to the lungs and enters each lung by branching into two main bronchi (left indicated in brown and right indicated in dark blue) at the anatomical point called the carina. The right main bronchus further splits into three lobar bronchi which enter three lobes of the right lung. Likewise, the left bronchus splits into two lobar bronchi for each left lung lobe. These bronchi undergo multiple divisions, forming the bronchial airway tree. Similar to the bronchial airway system, pulmonary vessels also branch throughout the lungs in a tree structure. The pulmonary vascular tree carries out the transportation of deoxygenated blood from the heart to the lungs to perform oxygenation, whereas the bronchial airway tree supports the flow of oxygen to the lung structures, including the pulmonary vessels [18]. Both of these trees enter and exit the lungs through a place called the hilum (denoted by the green dotted oval).

Figure 2b illustrates the lung anatomical structures on the CT scan. As we can see on the scan, there are two distinct components: the air (the black regions) and the human body (the gray regions) [17]. These two components have different radiography densities in which the air (−1000 HU) has a much lower density than the human body (−400 HU to 1000 HU). The human body consists of structures such as parenchyma or lung regions, fluid, fat, soft tissues, bones, and vessels. The radiological densities of these structures are different from each other showing different gray levels on the CT scan. Figure 3 demonstrates the range of radiological densities (HU values) of each lung structure.

3.1.2. Gray-Level Thresholding

Several researchers have proposed different segmentation methods for lung anatomical structures. We applied gray-level thresholding due to its quick and straightforward procedure. To segment the region of interest (ROI), thresholding replaces an image pixel with a black one if it has a gray level of less than a predefined threshold value.

$$\mathrm{If}g\left(P_{x,y}\right)< T, \mathrm{then} P_{x,y} = 0, \mathrm{else}1,$$

(1)

where $g\left(P_{x,y}\right)$ is the gray value of the image pixel $P_{x,y}$ and $T$ is the threshold gray value.

As we discussed, the lung anatomical structures are allocated in a particular gray-level range on a CT scan. They appear in a range between black and white; for instance, the air appears black, the fluid appears gray, soft tissues appear various shades of gray, bones appear dense white, and vessels appear white. However, every pixel of each specific region represents an individual gray value that is related to the mean radiographic density of the lung anatomical structures [19]. The relationship between the gray value of a pixel and its associated density can be expressed by

$$g\left(P_{x,y}\right)= \frac{HU-b}{m},$$

(2)

where $HU$ is the radiographic density, $b$ is the rescale intercept, and $m$ is the rescale slope of the CT image. Using this equation, we convert the HU values of the lung structures into gray values to set a proper threshold.

3.1.3. Isotropic Interpolation

Lung CT scans are two-dimensional (2D) cross-sectional images taken from different angles around the body. These slices can be stacked together and reconstructed into a three-dimensional (3D) isotropic image for more comprehensive analysis and visualization. Assume that $V\left(x,y,z\right)$ is 3D data of stacked CT slices with the dimensions $N_x \times N_y \times N_z$(width × height × thickness) where $N_x = N_y$ (generally it is equal to 512 which is the typical resolution of a 2D CT slice) and $N_z$ is the total number of slices in a single exam. Here, the term “single exam” means all of the sequential CT slices for a single patient during one CT scan. Then, the position of a voxel in $V$ can be expressed by $V\left(x_p,y_q,z_k\right)$ where:

$${\left\{x_p\right\}}_{p=0}^{N_x-1},{\left\{y_q\right\}}_{q=0}^{N_y-1} ,\mathrm{and}{\left\{z_k\right\}}_{k=0}^{N_z-1}.$$

(3)

For the CT scans, we can assume that $x_p= p\Delta x$, $y_q= q\Delta y,$ and $z_k= k\Delta z$ where ∆ denotes the intervals between pixels along each coordinate. In a situation with inevitable noise, the positions of the voxel are defined as

$$g\left(x_p,y_q,z_k\right)= V\left(x_p,y_q,z_k\right)+n\left(x_p,y_q,z_k\right)$$

(4)

where $n\left(x_p,y_q,z_k\right)$ represents the additive noise. After stacking the 2D slices, linear interpolation has to be carried out across the z-axis, because the thickness of the CT slices may vary even in a single exam:

$$g_{lin}\left(z\right)= \left(1-\frac{z- z_k}{z_{k+1}- z_k}\right)g\left(z_k\right)+ \left(\frac{z- z_k}{z_{k+1}- z_k}\right)g\left(z_{k+1}\right),z_k \le z \le z_{k+1}$$

(5)

where $z$ is the new slice to be interpolated, and $z_k$ and $z_{k+1}$ are two adjacent slices of $g\left(x,y,z\right).$ Then, $g_{lin}\left(z\right)$ is the resulting image after linear interpolation.

Some of the previous CAD methods reconstructed the volumetric structure CT slices at the beginning stage and then detection was performed on the reconstructed volume. Although working on the isotropic image provides comprehensive information about the tumor nodules, it demands high computational effort and time. Conversely, working on 2D data demands less effort but provides insufficient information about the tumor nodules. As an expedient method, we performed segmentation slice-by-slice on 2D data; after that, we reconstructed an isotropic image of 2D segments for further analysis.

3.1.4. Lung Region Segmentation

Lung regions constitute a large proportion of air with a radiographic density ranging from −600 HU to −400 HU on the CT scans. In keeping with the histogram of HU values in Figure 3, the CT value −400 HU separates the air-filled regions from the human tissues well. Thus, we chose −400 HU as the threshold density to segment the lung regions. The corresponding gray value of the selected density HU can be converted using Equation (2). With this threshold gray value, we performed segmentation by applying gray level thresholding.

As an illustration, Figure 4a shows a 2D image of lung CT scan where black portions represent air-filled regions and gray portions represent the human tissues. After thresholding using −400 HU, the body region can be eliminated by substituting it with black pixels, as illustrated in Figure 4b. However, we obtained two separate air-filled regions (white pixels): one outside of the eliminated body and another inside the body region. Our region of interest, the lungs, comprises air-filled regions inside the body. Thus, we suppressed all the white pixels outside of the body, as shown in Figure 4c.

After the suppression, we only had air-filled regions inside the body and these are the lung regions. Subsequently, the resulting lung regions were morphologically enclosed, as shown in Figure 4d. The aim of enclosing was to prevent under-segmentation of lesions inside the lungs, especially the tumor nodules which are adhered to the lung boundary. Moreover, we performed separation of the left and right lungs because they may touch each other in some CT slices. Morphological erosion can help to separate the two lungs, as shown in Figure 4e. For all sequential CT slices in a single exam, all the procedures from (a) to (e) were conducted slice by slice. After that, all resulting 2D lung segments were linearly interpolated to generate an isotropic image, as depicted in Figure 4f.

3.1.5. Trachea and Bronchial Tree Segmentation

Following the segmentation of the lung regions, the next step was to segment the trachea and bronchial tree. These two organs carry out the distribution of oxygen in the lungs and show air density on the CT scans, as depicted in Figure 5a. According to the lung anatomy, the trachea is a tube-like air-filled structure which is located between the two lungs, and it enters each lung by branching two main bronchi. Based on this fact, the lesions with air density were roughly segmented using the threshold density of −900 HU [20], as illustrated in Figure 5b. From these air-filled segments, a single lesion which locates the middle of the two lungs was segregated as the trachea, as shown in Figure 5c. Similar to the previous step, trachea segmentation was also executed slice-by-slice, and then the isotropic image was reconstructed. After the isotropic reconstruction, the tube-like structure of the segmented trachea was visualized, as in Figure 5c.

After tracheal segmentation, segmentation of the bronchial airways was attempted using 3D region growing. Using the center voxel of the segmented trachea as a seed point, region growing was iteratively performed based on different threshold values. Similar to [20], we set the initial threshold value as −900 HU and increased this by 64 HU in every iteration to find the airway regions. However, region growing may suffer from leakage of segmentation in some cases as the bronchial airways are spread throughout the lungs. For instance, Figure 5e depicts the leakage of bronchial airway segmentation into the parenchyma (lung regions). For such cases, the threshold value needed to be adjusted in each iteration to prevent leakage. If the total volume of the segmented airway tree in the current iteration was at least twice that of the previous iteration, region growth leakage was observed. Thus, the threshold value was reduced by half to stop the leakage. In this way, the trachea and the bronchial tree were successfully segmented, as shown in Figure 5f.

3.1.6. Pulmonary Vessel Segmentation

Pulmonary vessels have a complex structure with several branches spanning throughout the lung surfaces. They are elongated, tubular, and appear bright on the CT scans [21] as can be seen in Figure 6a. Generally, they have a soft-tissue density of approximately 40 HU [22]. However, we did not use this density value as a threshold because vessels are usually in contact with adjacent pulmonary structures such as airways and nodules.

As a prior process to vessel segmentation, we extract all of the lesions inside the segmented lungs by applying threshold density of −800 HU, as illustrated in Figure 6c. Among these segmented lesions, we extracted the vessels using multiscale vessel enhancement filtering [23]. This enhanced and discriminated the vessels from the interference lesions based on the eigenvalue analysis of the Hessian metric. As in the previous steps, vessels from 2D CT slices were segmented slice-by-slice, and then isotropic data was generated, as illustrated in Figure 6e.

3.1.7. Fissure Detection and Lung Lobe Segmentation

Pulmonary fissures are double layers of visceral-pleura and appear as bright lines spanning the parenchyma on the CT scan (Figure 7a). In order to segment the fissures correctly, prior anatomical knowledge is crucial. As we discussed in Section 3.1.1, fissures divide the lungs into five separate lobes. A fissure is treated as a boundary between the two lung lobes; thus, the bronchial airways and vessels cannot overpass it to enter the adjacent lobe. Based on this fact, the location of a fissure can be assumed to be a gap between the two lung lobes where the airways and vessels are clear. As with vessel segmentation, we began fissure segmentation by detecting all of the lesions inside the lungs, as depicted in Figure 7b,c. Subsequently, we enhanced the tubular lesions using Hessian-based filtering, as shown in Figure 7d. Among these tubular lesions, we found the longest continuous and non-branching lines across the lungs, as represented in Figure 7e. These lines were regarded as the possible fissure regions, and all fissure regions from 2D CT slices were segmented slice-by-slice. After achieving all 2D fissure segments, the isotropic structure of possible fissure lines was created, as in Figure 7f. From that figure, it is evident that the isotropic structure can give a more comprehensive view of fissure lines. The stacked fissure lines became plate-like structures in the isotropic view. However, there was some noise and incomplete parts in the fissure planes. Hence, we performed 3D morphological operations to remove the noise and enclose the incomplete parts. Finally, we successfully segmented the fissures by extracting three biggest planes, as illustrated in Figure 7g. To highlight the segmented fissures, we also provide transparent views of the isotropic images. Figure 7h shows a transparent view of the oblique and horizontal fissures, dividing the right lung into three lobes. Similarly, Figure 7i shows a transparent view of the oblique fissure dividing the left lung into two lobes. Subtracting these fissure planes from the segmented lung volumes (Section 3.1.4) gave five different lobes, as illustrated in Figure 7j.

3.1.8. Rib and Bone Segmentation

The ribs and bones are the highest-density lesions in the lungs. They appear as white on the CT scans, as illustrated in Figure 8a and possess a radiographic density ranging from 400 to 1000 HU. Thus, we can easily separate them from other pulmonary lesions by finding pixel values higher than 400 HU. As in the previous steps, an isotropic image of the ribs and bones can be generated using 2D segments from each slice. For illustration, Figure 8b represents the 2D segments and Figure 8c represents 3D segments of the ribs and bones.

3.1.9. Segmentation of Nodule Candidates

Nodules are soft tissue lesions exhibiting high potential to be cancer. In Figure 9a, we can see an example of a nodule (red-bordered) and other nodule-liked false lesions (yellow-bordered). For a clear visualization, a zoomed-in view of Figure 9a is provided in Figure 9b. Nodules can be divided into three types—solid, non-solid, and partly solid—depending on their radiological density. The first type, solid nodules, is found most frequently, and has a soft tissue density if isolated. In the case of vessel attachment, their contours become obscure. The second type, non-solid nodules, is inferred by vessel density and appears as a ground-glass structure. The last type, partly solid nodules, has a hybrid density of soft tissue and vessel.

To ensure the detection of all nodule types, the lesions inside the parenchyma were first segmented first using the threshold value −800 HU, as illustrated in Figure 9c. Then, an isotropic image of these internal lesions Figure 9d was reconstructed from 2D segments. Using this isotropic image, we attempted to extract possible nodule lesions, also known as nodule candidates. A nodule is a round or oval-shaped structure in a 2D CT scan, but it forms a blob-shaped structure in volumetric view. Thus, a blob enhancement filter can be applied to extract nodules. In Figure 9e, we can see the isotropic structures of the segmented nodule candidates. In this step, we cannot directly segment the true tumor nodules because there are many nodule-like structures in the lungs. These structures interfere with and make it troublesome to detect the real nodules. Since nodules are the signs of lung cancer, wrong or missed detection can seriously affect the patient. For this reason, nodule candidates are segmented first in this step, and then actual nodules are segregated with the help of a machine learning algorithm in the next detection phase.

3.2. Detection of the True Tumor Nodules

The primary issue of a lung cancer diagnosis is to detect the true tumor nodules. Discriminating true nodules from other interference lesions remains a challenge, because there is a high number of false positive lesions inside the lungs. In clinical practice, radiologists generally use several radiological features such as size, shape, margin and morphology to adequately identify a true tumor nodule. Based on these radiological criteria, some image features from each nodule candidate are extracted and fed into a classification algorithm to segregate the real tumor nodules.

3.2.1. Nodule Feature Extraction

Instead of extracting image features from 2D segments, we extracted features from each isotropic nodule candidate to get more precise measurements. We obtained 28 nodule features in total based on three major feature groups: geometric, intensity and texture.

The first group, geometric features, contains the most commonly used features for nodule detection. They can provide information about the physical appearance of tumor nodules. Four geometric features—volume, perimeter, equivalent diameter and sphericity—were extracted in this study.

The second group, intensity features, is also significant for tumor detection, because the intensity of the same parenchymal lesions has similar value. These features can be calculated by the first-order statistics of the histogram, and we extracted five intensity features, namely the average radiological density (HU), mean, standard deviation, skewness, and kurtosis.

In addition, the last group, texture features, is a great deal of help in identifying the true nodules. They can provide the inherent characteristics of nodules such as the constituents of air, fat, cavitation, and so forth [24]. They are the second-order statistical feature and are usually based on the gray-level co-occurrence matrix (GLCM). Nineteen textural features—autocorrelation, cluster prominence, cluster shade, contrast, correlation, different entropy, different variance, dissimilarity, energy, entropy, homogeneity, correlation1, correlation2, inverse difference, maximum probability, sum average, sum entropy, square variance, and sum variance—were extracted for texture analysis. For interested readers, detailed descriptions and mathematical calculations of these extracted features can be found in [25,26].

3.2.2. First Stage Classification

Once the features had been extracted from each isotropic nodule candidate, they were fed into the classification algorithm to select the true tumor nodules. Our proposed CAD has two stages of classification; the first stage intents to discriminate the true tumor nodules from other false lesions. On the other hand, the second stage intents to classify the associated stages of the truly predicted tumors. For both of the classification stages, we empirically chose the Back Propagation Neural Network (BPNN) due to its performance. The detailed experiments and a performance comparison of BPNN with other classifiers will be explained later in Section 4. As the BPNN is a particular type of artificial neural network (ANN), it also works on three fundamental layers (an input layer, one or more hidden layers, and an output layer). Unlike the ANN, BPNN can back propagate the learning to minimize the errors. The twenty-eight extracted nodule features become input neurons, and two classes (true-nodules and false-nodules) are outputs of the first stage of BPNN.

3.3. Staging

This phase is the key contribution of this research, because most current CADs are capable of tumor detection but not staging assessments. Staging measures the severity of lung cancer by determining how large the tumors and how much they have spread. Knowing the exact stage of a tumor can give a great deal of help in providing precise treatments for patients. Hence, it plays a vital role in increasing the patient’s survival rate. As we described earlier, our second-stage classification aims to perform the staging of true tumor nodules. To carry out this task, we reused the nodule features of truly predicted tumor by the first-stage classification. Furthermore, we extracted additional locational features to determine the invasion and spread of the tumors.

3.3.1. Locational Feature Extraction

Locational features are essential parameters for identifying the stages of lung cancer. They can provide information about the local extent or invasion of the primary tumors. As described in Table 1, the stages of tumors are highly associated with their locations. T1-staged tumors are located inside the lungs and in the lobar bronchus; T2-staged tumors invade the main bronchus, visceral pleura, and hilar regions; T3-staged tumors spread to the chest wall, phrenic nerve, and parietal pericardium; and finally, T4-staged tumors invade the diaphragm, mediastinum, heart, great vessels, and trachea. Considering these clinical descriptions, we extracted the locational features of the tumor nodules by dividing the lungs into different locational zones. The segmentation of lung anatomical structures in Section 3.1 gives a great deal of help for diving the locational zones.

Firstly, we divided the isotropic structure of the trachea and bronchial airway tree (Section 3.1.5) into three different zones. The first zone (Zone 1) represents the regions of the trachea; the second zone (Zone 2) represents the regions of the main bronchus and hilar regions, and the third zone (Zone 3) represents the region of the lobar bronchus. To determine these three zones, the 3D skeletonization method [27] was applied. This method iteratively erodes the image voxels until only a single-voxel centerline is achieved. Figure 10 depicts an isotropic image of the trachea and bronchial airway tree. In the figure, the red thin-centerline represents the skeleton of the isotropic image.

From this centerline, we tried to detect the branching points, because the trachea branches into two main bronchi at a point called the carina. The first branching point of the centerline can be designated as the place of the carina. Based on this point, we determined the upper portion of the carina as the region of the trachea (Zone 1). Similarly, the regions between the carina point and the next branching points were defined as Zone 2—the areas of the main bronchus and hilar. Then, the other portion was assigned as the Zone 3—the lobar bronchus.

Once these three zones had been defined, the next location was the region of the chest wall (Zone 4). The chest wall is an organ that surrounds and protects the lungs. It is comprised of bones especially the ribs, sternum, and spine. This zone was easily defined because the ribs and bones had already been segmented, as described in Section 3.1.8. Another location was the pulmonary vessels (Zone 5). As in zone 4, this zone was easily defined using the vessel segments described in Section 3.1.6. Next, zone 6 included the regions of the mediastinum, heart, phrenic nerve, and parietal pericardium. We classified these organs together into Zone 6 because they are located inside the mediastinum, the region between the two lungs. The right and left lungs segments can help with the identification of this zone, and the area between the two lungs can be regarded as Zone 6. Finally, Zone 7 was defined as the location of the diaphragm, which is the portion below the lungs. To identify zones 6 and 7, the segments of the lung regions described in Section 3.1.4 were applied. For a clear understanding, the locational zones and associated tumor stages are summarized in

Table 2. Dividing different zones.

Lung Zones	Regions Invaded	Associated Tumor Stages
Zone 1	Trachea	T4
Zone 2	Main bronchus and hilar	T2
Zone 3	Lobar bronchus	T1
Zone 4	Chest wall	T3
Zone 5	Pulmonary vessels	T4
Zone 6	Mediastinum, heart, phrenic nerve, and parietal pericardium	T3, T4
Zone 7	Diaphragm	T4

. Moreover, a graphical representation of these zones is also presented in Figure 11.

The idea behind dividing the lungs into different locational zones is to check the invasion of the tumor nodules. This task can be accomplished by calculating the 3D convex hull and comparing the coordinate values. The convex hull of a region can be calculated by finding the smallest convex polygon which encloses all of the points of that region. In this study, we applied the Quick hull algorithm [28], because it can handle high dimension problems. As we were working on the 3D volumetric data, the algorithm returned a $p-by-3$ matrix, where $p$ is the total number of vertex points of the polygon and shows each point with three coordinate values $\left(x, y, z\right).$ Assuming $T$ is a tumor nodule, $Lz$ is a specific locational zone (any of zone from Zone 1 to Zone 7 is possible). We checked the invasion of $T$ to the $Lz$ using the invasion checking Algorithm 1 described below.

Algorithm 1. Invasion checking

Calculate the convex hulls of $T$ and $Lz$ and name them $C_T$ and $C_{Lz}$ respectively. Both of them are the $p$-by-3 matrixes, where $p$ is the number of vertices in the convex polygon, and each vertex has $x,y$ and $z$ coordinate values. Assign the initial status of invasion with a Boolean value such that $Invasion=0$. From $C_T$, find six values which are the minimum and maximum of each coordinate. Let us say that $\min C_{Tx}$ and $\max C_{Tx}$ are the minimum and maximum values among the $x$ coordinate points. In this way, $\min C_{Ty}$, $\max C_{Ty}$, $\min C_{Tz},$ and $\max C_{Tz}$ are also calculated from the $y$ and $z$ coordinates points. Similar to step 3, calculate another six values from $C_{LZ}$. They are $\min C_{LZx}$, $\max C_{LZx}$, $\min C_{LZy}$, $\min C_{LZy}$, $\min C_{LZy}$ and $\min C_{LZy}$. Based on these values, check whether $T$ is located inside or outside of $LZ$. If $\min C_{Tx}$ > $\min C_{LZx}$ and ${\min }_{Ty}$>$\min C_{LZy}$ and $\min C_{Tz}$> $\min C_{LZz}$ and $\max C_{Tx}$ < $\max C_{LZx}$ and ${\max }_{Ty}$ < $\max C_{LZy}$ and $\max C_{Tz}$< $\max C_{LZz},$ then the convex polygon of $T$ geometrically locates inside that of $Lz$ and is assigned the value $Invasion=1.$

Generally, tumor nodules are isolated inside the lungs, but in some cases they may attach to the visceral pleura. In order to investigate this, we first checked whether the tumor nodule was inside or outside of the lung regions. For this task, we used the previously described checking algorithm again. Here, $Lz$ became the lung regions instead of the locational zones. Once the tumor nodule was located inside the lungs, we needed to check whether the nodule was attached to the pleura or not. For this task, the following steps of the pleural attachment checking Algorithm 2 were performed.

Algorithm 2. Pleural attachment checking

$L$ is one of the lungs (left or right lung), and $T$ is the tumor nodule. Both $L$ and $T$ are three dimensional arrays (512 × 512 × number of slices in a single exam). Firstly, convert both arrays into logical arrays by changing all the voxels values into 1 and 0. Assign a Boolean value to the initial status of pleural attachment such that $Pleural attachment=0.$ Find the edge voxels of the logical array $L,$ and define it as $E$. Calculate the logical negation of $E$ from $T$ and assign the results into a temporary array called $Tmp$ such that $Tmp=T \left(~E\right).$ Check whether $Tmp$ has any values of 1 or not. If there is a value of 1, some part of the tumor is along the edge of the lung region. Modify the status of pleural attachment to $Pleural attachment=1.$

After checking for pleural attachment, another essential feature is the number of tumor nodules in the lungs. This feature can be achieved by counting the total number of true predicted nodules in a single exam. If a patient has more than one nodule, the locations of the satellite nodules must be considered for tumor staging. If the tumors are in the same lobe, this indicates the T3 stage, whereas if they are in different lobes, this indicates the T4 stage. In order to know whether the tumors are in the same lobe or different lobes, we needed to define the invasion of tumor nodules into a specific lobe. Thus, we used the invasion checking algorithm again, but $Lz$ became a particular lobe of lungs. Based on the invasion results, we made five flags for lobe invasion: $rightupperlobe=1$, $rightmiddlelobe=2$, $rightlowerlobe=3,$ $lefupperlobe=4$ and $leflowerlobe=5$. As a summary, the locational features extracted in this section and their return values are described in

Table 3. Locational features.

Features	Description	Returns
Invasion	Determines the invasion of tumor nodules into different zones and returns zone numbers.	1, 2, 3, 4, 5, 6, 7
Pleural attachment	Determines whether the tumor nodules attach the visceral pleura or not and returns Boolean value (0 = not pleural attachment and 1 = pleural attachment).	0,1
Count	Calculates the number of true predicted tumor nodules in a single exam and returns an integer value n.	1, … , n
Lobe location	Determines which lobe the tumor nodules exist in and return the lobe numbers.	1, 2, 3, 4, 5

.

3.3.2. Second-Stage Classification

The second-stage classification aims to classify the true tumor nodules into different T-stages. As in the first stage, BPNN is applied in this stage. However, the first stage classification is a binary classification problem that only predicts two classes (true tumor nodules and false tumor nodules). Unlike the first stage classification, the second stage classification is a multi-classification problem that predicts seven clinical stages of tumors, namely T0/Tis, T1a, T1b, T2a, T2b, T3 and T4. Stage Tx is neglected in the classification because tumor nodules cannot be detected on the CT scans at that stage. In the first-stage classification, we used twenty-eight nodule features to segregate the true tumor nodules. After detecting a true tumor nodule, the associated nodule features of that nodule were carried to the staging phase, as depicted in Figure 1. Then, four locational features (described in Table 3) were added to determine the tumor stages in second-stage classification. Therefore, the total number of features fed into the second-stage BPNN was thirty-two, and the number of output classes was seven.

4. Experimental Results

In this study, we propose a CAD that is capable of detecting and staging of the pulmonary tumors for lung cancer diagnosis. This CAD was developed and evaluated using four datasets, namely LIDC-IDRI [29,30], NSCLC-Radiomics-Genomics [2,31], NSCLC-Radiomics [2,32], and NSCLC Radiogenomics [33,34] (Supplementary Materials) where NSCLC stands for non-small cell lung cancer. These datasets are downloadable from The Cancer Imaging Archive (TCIA) [35] which is an open source of medical images for scientific and educational research. Expert radiologists confirmed all of the tumor nodules in these datasets, and the clinical diagnosis results were also provided. We applied these results as the gold standard to evaluate the performance of proposed CAD.

Table 4. Detailed descriptions of the datasets applied.

Dataset	Descriptions	Number of Exams Used
LIDC-IDRI	Contains 1010 thoracic CT scans of lung cancer patients and an associated XML file that shows the true nodule annotations.	888
NSCLC-Radiomics-Genomics	Contains 89 CT scans from non-small cell lung cancer patients who underwent surgery. The clinical data of tumor stages is also available.	89
NSCLC-Radiomics	Contains 422 CT scans from non-small cell lung cancer patients. Three-dimensional manual delineation and clinical results by radiologist are available.	422
NSCLC Radiogenomics	Contains 211 CT, PET/CT scans of non-small cell lung cancer patients. Both annotation files and clinical data are also provided.	211

presents detailed descriptions of each dataset used in this study.

As described earlier, our CAD has two primary purposes: detection and staging. The first purpose is more fundamental for the production of accurate diagnosis results because the correctly predicted tumor nodules from the first stage are further applied for staging. Among the datasets mentioned above, the LIDC-IDRI only provides XML files for the true nodule annotations. The clinical stages of the tumor nodules are not available in LIDC-IDRI. Therefore, we applied it only for the detection stage. Moreover, it is a huge dataset and had been employed by several researchers to develop CADs for nodule detection. There are 1010 exams in the LIDC-IDRI dataset, but only 888 exams were applied for our experiment because some exams contain missing and inconsistent slices. The application of LIDC-IDRI for the first purpose, detection, also acted as a separate validation for more robust detection.

Unlike LIDC-IDRI, the three NSCLC datasets can provide the data for clinical stages of tumor. Thus, we applied these three datasets for the second purpose. Indeed, the CT exams from these three datasets had to pass through the first stage classification to segregate the true tumor nodules. Subsequently, the true predicted tumors were categorized into different clinical stages by the second-stage classifier. Therefore, the first stage of classification was double validated by not only LIDC-IDRI, but also NSCLC.

However, the second stage of classification is a multi-classification problem that outputs seven classes. Class 1 represents T1a, class 2 represents T1b, class 3 represents T2a, class 4 represents T2b, class 5 represents T3, class 6 represents T5, and class 7 represents T0/Tis. The NSCLC datasets contain a different number of samples for each class, and the class distribution is profoundly different, as described in Figure 12. In this figure, it is evident that there were few samples for class 6 (T5) and class 7 (T0/Tis). After removing the missing-class samples, the total number of samples from three NSCLC datasets became 672 and they were used for staging.

Before we started the experiment, we performed the preparation of the data for training and testing. As the data in the real world is fuzzy in nature, we validated our CAD using repeated random trials. Figure 13 shows the preparation of data for repeated random trials in both first and second stage classifications. For first stage classification, the samples in the LIDC-IDRI dataset (888 samples) were randomly divided into five splits 50%-50%, 60%-40%, 70%-30%, 80%-20% and 90%-10% for training and testing. Similarly, for the second stage classification, samples in the NSCLC datasets (672 samples) were randomly divided into five trials. In each split, we repeatedly selected random samples $k=100$ times as described in the figure. Since the samples were randomly selected, each iteration $k$ generated different samples for training and testing. We trained and tested five different classifiers namely the Decision Tree (DT), K-nearest neighbor (KNN), Support Vector Machine (SVM), Ensemble Tree (ET), and the Back Propagation Neural Network (BPNN) on these random samples. In each iteration we calculated the performance measures of each classifier then calculated the mean and standard deviation of performance measures for each split.

The performance measurements which were calculated for each classifier are accuracy, sensitivity, specificity, precision, and the F-score. They can be computed by:

$$accuracy= \frac{TP+TN}{TP+TN+FP+FN}$$

(6)

$$sensitivity\left(recall\right)= \frac{TP}{TP+FN}$$

(7)

$$specificity= \frac{TN}{FP+TN}$$

(8)

$$precision= \frac{TP}{FP+TP}$$

(9)

$$F1-score = 2*\frac{Precision*recall}{Precision+recall}$$

(10)

Nonetheless, the second stage of classification is a multi-classification problem unlike the first; it is therefore more complex to evaluate the performance. To solve this problem, we used the “one versus the rest method”, which calculates the performance of the classifier for an individual class and then calculates the overall performance. For example, $C_i \left(i=1,2, \dots ,l\right)$ is an individual class of a multi-classification problem, and $l$ is the total number of classes. From the counts of $Ci$, the assessments $T{P}_i$, $T{N}_i$, $F{P}_i$ and $F{N}_i$ were obtained. Then, the overall performance of the classifier for all classes was calculated by:

$$accuracy= \frac{{{\displaystyle \sum }}_{i=1}^l\frac{T{P}_i+T{N}_i}{T{P}_i+T{N}_i+F{P}_i+F{N}_i}}{l}$$

(11)

$$sensitivity= \frac{{{\displaystyle \sum }}_{i=1}^l\frac{T{P}_i}{T{P}_i+F{N}_i}}{l}$$

(12)

$$specificity= \frac{{{\displaystyle \sum }}_{i=1}^l\frac{T{N}_i}{T{N}_i+F{P}_i}}{l}$$

(13)

$$precision= \frac{{{\displaystyle \sum }}_{i=1}^l\frac{T{P}_i}{T{P}_i+F{P}_i}}{l}$$

(14)

$$F1-score= \frac{{{\displaystyle \sum }}_{i=1}^l\left(2*\frac{Precisio{n}_i*recal{l}_i}{Precisio{n}_i+recal{l}_i}\right)}{l}$$

(15)

In addition to these measurements, we also take into account the area under the curve (AUC) and execution time of each classifier for performance evaluation.

Table 5. Comparison of performance measurements generated by five different classifiers for first-stage classification.

Mean(±Standard Deviation) of Performance Assessments for 100 Random Iterations
Classifiers	Measurements	50%-50%	60%-40%	70%-30%	80%-20%	90%-10%
DT	Accuracy	0.82(±0.02)	0.82(±0.02)	0.83(±0.02)	0.83(±0.03)	0.83(±0.03)
	Sensitivity	0.79(±0.03)	0.79(±0.03)	0.80(±0.03)	0.81(±0.05)	0.81(±0.06)
	Specificity	0.86(±0.02)	0.86(±0.03)	0.86(±0.03)	0.86(±0.04)	0.86(±0.05)
	Precision	0.85(±0.02)	0.85(±0.03)	0.85(±0.03)	0.85(±0.04)	0.85(±0.04)
	F1-score	0.82(±0.02)	0.82(±0.02)	0.82(±0.02)	0.83(±0.03)	0.83(±0.04)
	AUC	0.92(±0.01)	0.92(±0.01)	0.93(±0.01)	0.93(±0.02)	0.93(±0.02)
	Time	0.10(±0.07)	0.10(±0.04)	0.13(±0.06)	0.14(±0.06)	0.15(±0.04)
KNN	Accuracy	0.87(±0.01)	0.87(±0.02)	0.87(±0.02)	0.87(±0.02)	0.88(±0.03)
	Sensitivity	0.85(±0.03)	0.85(±0.03)	0.86(±0.03)	0.85(±0.04)	0.85(±0.05)
	Specificity	0.89(±0.03)	0.89(±0.03)	0.89(±0.03)	0.89(±0.04)	0.90(±0.04)
	Precision	0.89(±0.02)	0.89(±0.03)	0.88(±0.03)	0.89(±0.03)	0.90(±0.04)
	F1-score	0.87(±0.02)	0.87(±0.02)	0.87(±0.02)	0.87(±0.03)	0.87(±0.03)
	AUC	0.95(±0.01)	0.95(±0.01)	0.95(±0.01)	0.95(±0.01)	0.95(±0.02)
	Time	0.05(±0.14)	0.05(±0.12)	0.05(±0.13)	0.06(±0.16)	0.05(±0.12)
SVM	Accuracy	0.84(±0.02)	0.84(±0.02)	0.85(±0.02)	0.85(±0.02)	0.85(±0.03)
	Sensitivity	0.79(±0.03)	0.79(±0.03)	0.80(±0.03)	0.80(±0.04)	0.80(±0.06)
	Specificity	0.89(±0.02)	0.90(±0.02)	0.90(±0.02)	0.91(±0.03)	0.91(±0.04)
	Precision	0.88(±0.02)	0.89(±0.02)	0.89(±0.02)	0.90(±0.03)	0.90(±0.04)
	F1-score	0.84(±0.02)	0.84(±0.02)	0.84(±0.02)	0.84(±0.03)	0.85(±0.04)
	AUC	0.91(±0.01)	0.91(±0.02)	0.92(±0.01)	0.93(±0.02)	0.93(±0.02)
	Time	0.06(±0.07)	0.06(±0.04)	0.08(±0.07)	0.09(±0.06)	0.11(±0.04)
ET	Accuracy	0.86(±0.02)	0.86(±0.02)	0.86(±0.02)	0.86(±0.03)	0.86(±0.03)
	Sensitivity	0.81(±0.03)	0.81(±0.03)	0.81(±0.03)	0.81(±0.04)	0.81(±0.06)
	Specificity	0.90(±0.02)	0.90(±0.02)	0.90(±0.03)	0.91(±0.03)	0.91(±0.04)
	Precision	0.89(±0.02)	0.90(±0.02)	0.89(±0.03)	0.90(±0.04)	0.90(±0.04)
	F1-score	0.85(±0.02)	0.85(±0.02)	0.85(±0.02)	0.85(±0.03)	0.85(±0.04)
	AUC	0.93(±0.01)	0.93(±0.02)	0.93(±0.01)	0.93(±0.02)	0.93(±0.02)
	Time	0.48(±0.17)	0.45(±0.16)	0.51(±0.15)	0.53(±0.15)	0.54(±0.11)
BPNN	Accuracy	0.92(±0.01)	0.93(±0.02)	0.93(±0.02)	0.93(±0.02)	0.93(±0.02)
	Sensitivity	0.93(±0.02)	0.93(±0.03)	0.94(±0.03)	0.94(±0.03)	0.94(±0.04)
	Specificity	0.91(±0.03)	0.92(±0.03)	0.92(±0.03)	0.92(±0.03)	0.92(±0.04)
	Precision	0.91(±0.02)	0.92(±0.03)	0.92(±0.03)	0.92(±0.03)	0.92(±0.04)
	F1-score	0.92(±0.02)	0.93(±0.02)	0.93(±0.02)	0.93(±0.02)	0.93(±0.03)
	AUC	0.96(±0.02)	0.97(±0.02)	0.97(±0.02)	0.97(±0.01)	0.97(±0.02)
	Time	0.58(±0.17)	0.57(±0.22)	0.67(±0.18)	0.72(±0.15)	0.76(±0.17)

shows the mean and standard deviation of performance measurements obtained from each classifier in the first stage classification.

Similarly,

Table 6. Comparison of performance measurements generated by five different classifiers for second-stage classification.

Mean(±Standard Deviation) of Performance Assessments for 100 Random Iterations
Classifiers	Measurements	50%-50%	60%-40%	70%-30%	80%-20%	90%-10%
DT	Accuracy	0.79(±0.03)	0.76(±0.03)	0.75(±0.03)	0.74(±0.03)	0.73(±0.03)
	Sensitivity	0.62(±0.08)	0.58(±0.07)	0.58(±0.06)	0.58(±0.06)	0.56(±0.05)
	Specificity	0.96(±0.01)	0.95(±0.01)	0.95(±0.01)	0.95(±0.00)	0.95(±0.01)
	Precision	0.85(±0.03)	0.85(±0.03)	0.84(±0.04)	0.83(±0.03)	0.83(±0.03)
	F1-score	0.63(±0.08)	0.59(±0.07)	0.59(±0.06)	0.59(±0.07)	0.57(±0.06)
	AUC	0.71(±0.05)	0.69(±0.07)	0.68(±0.04)	0.68(±0.04)	0.67(±0.04)
	Time	0.05(±0.16)	0.05(±0.14)	0.05(±0.14)	0.06(±0.13)	0.06(±0.13)
KNN	Accuracy	0.55(±0.04)	0.57(±0.03)	0.59(±0.04)	0.61(±0.04)	0.62(±0.03)
	Sensitivity	0.58(±0.05)	0.58(±0.04)	0.50(±0.05)	0.60(±0.05)	0.53(±0.05)
	Specificity	0.91(±0.01)	0.92(±0.01)	0.92(±0.01)	0.93(±0.01)	0.93(±0.01)
	Precision	0.67(±0.08)	0.71(±0.04)	0.70(±0.07)	0.72(±0.07)	0.73(±0.06)
	F1-score	0.52(±0.15)	0.54(±0.12)	0.55(±0.15)	0.54(±0.17)	0.58(±0.14)
	AUC	0.48(±0.05)	0.50(±0.04)	0.51(±0.05)	0.52(±0.05)	0.53(±0.04)
	Time	0.04(±0.04)	0.04(±0.04)	0.04(±0.04)	0.06(±0.04)	0.06(±0.05)
SVM	Accuracy	0.46(±0.14)	0.45(±0.12)	0.50(±0.12)	0.52(±0.13)	0.52(±0.11)
	Sensitivity	0.62(±0.11)	0.60(±0.11)	0.66(±0.09)	0.67(±0.11)	0.67(±0.10)
	Specificity	0.91(±0.02)	0.91(±0.02)	0.92(±0.02)	0.92(±0.02)	0.92(±0.02)
	Precision	0.48(±0.12)	0.47(±0.10)	0.50(±0.09)	0.52(±0.10)	0.50(±0.09)
	F1-score	0.66(±0.16)	0.69(±0.15)	0.65(±0.13)	0.62(±0.14)	0.66(±0.13)
	AUC	0.54(±0.12)	0.53(±0.11)	0.57(±0.09)	0.58(±0.10)	0.57(±0.09)
	Time	0.36(±0.08)	0.37(±0.07)	0.35(±0.07)	0.45(±0.13)	0.41(±0.15)
ET	Accuracy	0.94(±0.03)	0.91(±0.03)	0.89(±0.03)	0.88(±0.03)	0.87(±0.03)
	Sensitivity	0.56(±0.32)	0.63(±0.28)	0.73(±0.18)	0.73(±0.21)	0.79(±0.07)
	Specificity	0.98(±0.01)	0.98(±0.01)	0.98(±0.01)	0.98(±0.01)	0.98(±0.01)
	Precision	0.92(±0.06)	0.93(±0.05)	0.94(±0.03)	0.94(±0.04)	0.95(±0.01)
	F1-score	0.57(±0.33)	0.65(±0.28)	0.75(±0.19)	0.75(±0.22)	0.81(±0.08)
	AUC	0.63(±0.36)	0.71(±0.30)	0.80(±0.19)	0.79(±0.22)	0.86(±0.05)
	Time	0.29(±0.11)	0.29(±0.10)	0.29(±0.10)	0.37(±0.13)	0.33(±0.14)
BPNN	Accuracy	0.90(±0.05)	0.90(±0.03)	0.91(±0.02)	0.91(±0.02)	0.91(±0.02)
	Sensitivity	0.84(±0.09)	0.79(±0.08)	0.78(±0.08)	0.74(±0.08)	0.72(±0.07)
	Specificity	0.98(±0.00)	0.97(±0.01)	0.98(±0.01)	0.97(±0.00)	0.97(±0.01)
	Precision	0.96(±0.02)	0.95(±0.02)	0.93(±0.02)	0.93(±0.02)	0.92(±0.02)
	F1-score	0.85(±0.08)	0.81(±0.08)	0.80(±0.08)	0.77(±0.08)	0.75(±0.07)
	AUC	0.89(±0.05)	0.86(±0.05)	0.85(±0.05)	0.82(±0.05)	0.81(±0.04)
	Time	0.48(±0.11)	0.48(±0.08)	0.48(±0.09)	0.62(±0.16)	0.59(±0.20)

describes the comparison of performance measurements generated by the five different classifiers for the second stage classification.

For graphical representation, box-plot distributions were applied to compare the performance of five alternative classifiers. Figure 14 illustrates the box-plots comparison between mean performance measurements generated by each classifier in first stage classification. Similarly, Figure 15 shows the box-plots comparison for second stage classification. Analyzing the distributions of box-plots, we can know that BPNN offers significantly higher performance than other classifiers in first stage classification. However, for the second stage classification, the performance of classifiers declined compared to the first stage because of class imbalance in the samples. The performance of DT, KNN and SVM decreased, and it indicates that they are not robust enough for random data with class imbalance. On the other hand, the ET and BPNN are robust for random data. The performance of ET seemed better than BPNN especially in specificity and precision because its box-plots had upper middle lines (higher median values) and small range of whiskers (condense data). But in other assessments such as accuracy, sensitivity, F1-score and AUC, BPNN showed higher values. Therefore, we decided to use BPNN for both stages of classification. As a result, BPNN reached an accuracy of 92.8%, a sensitivity of 93.6%, a specificity of 91.8%, a precision of 91.8%, an F1-score of 92.8% and an AUC of 96.8% for detection. For staging, it achieved an accuracy of 90.6%, a sensitivity of 77.4%, a specificity of 97.4%, a precision of 93.8%, an F1-score of 79.6% and an AUC of 84.6% respectively. Even though BPNN took more execution time, it can guarantee random and imbalanced samples.

As an example, the outputs of our proposed CAD are illustrated in Figure 16. They demonstrate 3D visualizations of tumors of different stages. Figure 16a represents a stage T1a tumor that is 1.83 cm in its greatest dimension and is located in the left lower lobe in an isolated manner. Figure 16b demonstrate a stage T1b tumor which is also located in the left lower lob, but is bigger in size (2.14 cm) than the tumor in Figure 16a.

Then, Figure 16c,d represents stage T2a and T2b tumors, respectively. Both tumors are located in the right upper lobes. The tumor in Figure 16c is 3.05 cm in its greatest dimension and is isolated, whereas the tumor in Figure 16d is 2.10 cm and touches the visceral pleural. Hence, the tumor in Figure 16d has a higher stage even though is smaller in size.

Figure 16e,f illustrates the stage T3 tumors. The tumor in Figure 16e is located in the right upper lobe and invades the chest wall. Also, Figure 16f demonstrates the presence of satellite nodules in the same lobe, the right upper lobe. Unlike Figure 16f, the tumors in Figure 16g contain satellite nodules in different lobes: one is in the right middle lobe, and another is in the left upper lobe. Thus, it is classified as stage T4. Finally, in Figure 16h, we can see a T4-staged tumor nodule which invades the mediastinum.

Moreover, we compared the performance of our proposed CAD with methods presented in previous works, as stated in

Table 7. Quantitative performance comparison of the proposed CAD method with methods presented in previous works.

CADs	Methods	Dataset	Samples	Accuracy
[10]	Gabor filter Marker-controlled watershed Geometric features (area, perimeter, eccentricity) SVM	NIHINCI Lung Image Consortium (LIDC)	40	Not described
[11]	Sharpening Marker-controlled watershed Area, perimeter, eccentricity, convex area, mean intensity Thresholding Random tree	Regional Cancer Centre Trivandrum	200	94.4%
[12]	Median filter Watershed transform Textural features Multi-class SVM classifier	Local dataset (JPEG format) UCI lung dataset (for training SVM)	500	Detection—97% Staging—87%
[14]	3D bounding boxes (manual) CNN	Institutional dataset (FDG-PET)/CT	472	Staging—90%
[15]	K-means clustering Double CDNN	LONI dataset	95	Detection—99.6%
Proposed method	HU-based thresholding 3D nodule features (geometric, textural, intensity) and locational features Double-staged BPNN	LIDC-IDRI NSCLC Radiomics-Genomics NSCLC-Radiomics NSCLC Radiogenomics	1560	Detection—92.8% Staging—90.6%

. It was difficult to make a fair comparison because the CADs were developed using different datasets, different numbers of samples, and different methods. Thus, we could only make a quantitative comparison of the performance outcomes. Based on these quantitative comparative results, it is evident that our proposed CAD is validated using not only higher amount, but also random samples, and it can provide preferable performance in both detection and staging.

5. Discussion and Conclusions

This paper presents a CAD capable of the detection and staging of lung tumors from computed tomography (CT) scans. Our CAD has two major contributions. The first contribution is the extraction of locational features from tumor nodules for the T-staging of lung cancer. The second is the double use of the BPNN classifier for the detection and staging of the tumor nodules.

The CAD works in three pivotal phases called segmentation, detection, and staging. A single CT exam of a patient containing multiple 2D slices is an input of the proposed CAD. From each input exam, the lung anatomical structures, such as the lung regions, trachea, bronchial airway tree, pulmonary vessels, fissures, lobes, and nodule candidates, are initially segmented using gray-level thresholding and isotropic interpolation methods. Subsequently, 28 nodule features are extracted from the segmented nodule candidates to detect the true tumor nodules. These features include four geometric, five intensity, and nineteen texture features. Using these features, the first stage of classification is performed and the true tumor nodules are segregated.

Once the true tumor nodules have been achieved, the locational features are added for staging. With the help of the segmented lung anatomical structures from the first phase, the locational features can be defined by dividing the lungs into different zones. Moreover, the invasion and attachment of the tumor nodules to other pulmonary organs are also checked by using the 3D quick hull algorithm and logical array checking. As well as this, the number of true tumor nodules predicted in a single test and their lobe locations are also extracted in this stage. Using these features, the staging of tumor nodules is conducted by second-stage classification. In this study, we applied the BPNN for both classifications. Before selecting the BPNN, we tested and compared it with five alternative classifiers using repeated random trials. Based on the comparative results, we determined that the BPNN should be used due to its high performance and robustness.

Our proposed CAD was developed and tested using 1560 CT exams from four popular public datasets: LIDC-IDRI, NSCLC-Radiomics-Genomics, NSCLC-Radiomics and NSCLC Radiogenomics. In the performance evaluation, our proposed CAD achieved a detection accuracy of 92.8%, a sensitivity of 93.6%, a specificity of 91.8%, a precision of 91.8%, an F-score of 92.8%, and an AUC of 96.8%. For the staging, we achieved an accuracy of 90.6%, a sensitivity of 77.4%, a specificity of 97.4%, a precision of 93.8%, an F1-score of 79.6% and an AUC of 84.6% respectively. Compared with previous works, our CAD was evaluated with more samples and obtained auspicious performances.

Unlike most existing CADs for lung cancer diagnosis, our CAD makes possible not only the detection, but also the staging of lung tumor nodules. Our first contribution, the extraction of locational features, has advantages for the staging of tumor nodules, because the severity of lung cancer is strongly associated with the size and location of tumor nodules. Knowing the exact location of tumors reflects accurate staging. Patient survival rates can also be increased by providing precise treatment options depending on the tumor stage. Moreover, locational features produced by our CAD will be useful for the clinical surgery planning of seriously staged tumors. The next contribution, the double stage of classification using BPNN, makes the CDA more robust. As the first stage classification filters only the true tumor nodules, we do not need to extract the locational features from all nodule candidates; this saves both computational effort and time. Nonetheless, our study has some limitations in terms of the need for background knowledge for anatomical lung structures. Moreover, our CAD only focuses on the T-staging of lung cancer. Thus, there are some open issues which can be further upgraded for the N and M-staging of lung cancer.