Study of the Hygrothermal Behavior of Wood Fiber Insulation Subjected to Non-Isothermal Loading
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Experimental Setup
- Better understand the hygrothermal phenomena involved during the transfer.
- Obtain sufficient data to validate or build predictive Heat, Air and Moisture transfer models.
- Characterize transport properties at the wall scale.
2.3. Numerical Model
2.4. Studied Loading
3. Results and Discussion
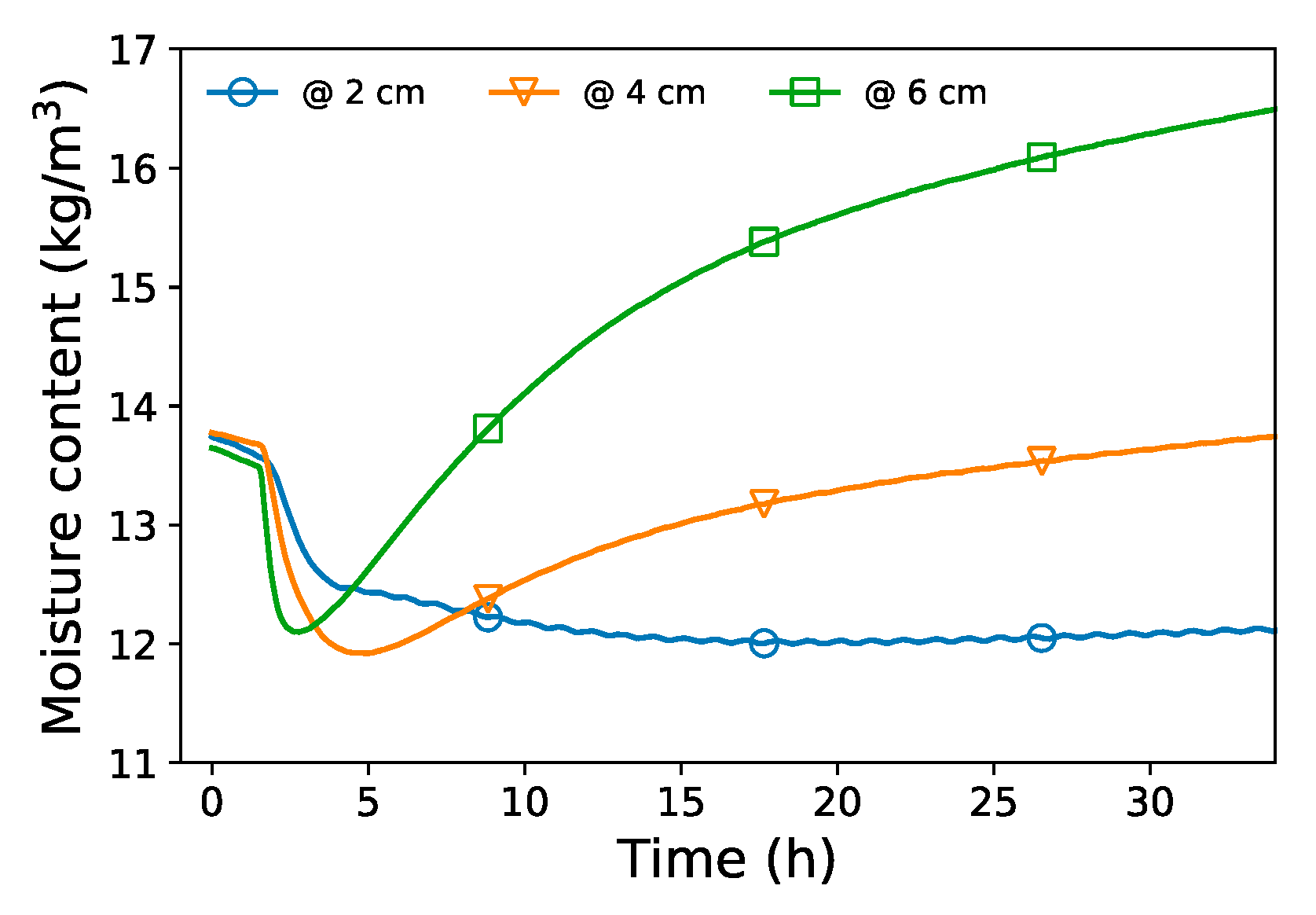
3.1. Experimental Analysis
3.2. Comparison of Experimental Results with Numerical Codes
4. Conclusions
- The redistribution of water which took place as the heat gradient developed. The water migrated from the warmest side to the coolest side.
- The model developed proved efficient at reproducing hygrothermal behavior under non-isothermal stresses.
- The variances between the measures—model were greater during the start-up phase.
- The latent effects could be detected and highlighted experimentally and numerically by comparison with the purely diffusive heat model.
Author Contributions
Funding
Conflicts of Interest
References
- ADEME. Les Chiffres clés du Bâtiment Énergie—Environnement; ADEME: France, 2013. [Google Scholar]
- Décret n° 2010-1269 du 26 Octobre 2010 Relatif aux Caractéristiques Thermiques et à la Performance Énergétique des Constructions. France. 2010.
- Kuenzel, H.M.; Holm, A.; Sedlbauer, K.; Antretter, F.; Ellinger, M. Moisture Buffering Effect of Interior Linings Made from Wood or Wood Based Products; IBP Report HTB-04/2004/e; Fraunhofer Institute of Building Physics: Holzkirchen, Germany, 2004. [Google Scholar]
- Rode, C.; Mendes, N.; Grau, K. Evaluation of Moisture Buffer Effects by Performing Whole-Building Simulations; ASHRAE Transactions: Nashville, TN, USA, 2004; pp. 783–794. [Google Scholar]
- Hameury, S. Moisture buffering capacity of heavy timber structures directly exposed to an indoor climate: A numerical study. Build. Environ. 2005, 40, 1400–1412. [Google Scholar] [CrossRef]
- Roels, S.; Depraetere, W.; Carmeliet, J.; Hens, H. Simulating non-isothermal water vapour transfer: An experimental validation on multi-layered building components. J. Build. Phys 1999, 23, 17–40. [Google Scholar]
- Philip, J.R.; De Vries, D.A. Moisture movement in porous material under temperature gradients. Trans. Am. Geophys. Union 1957, 38, 222–232. [Google Scholar] [CrossRef]
- Talukdar, P.; Olutmayin, S.O.; Osanyintola, O.F.; Simonson, C.J. An experimental data set for benchmarking 1-D, transient heat and moisture transfer models of hygroscopic building materials. Part I: Experimental facility and material property data. Int. J. Heat Mass Transf. 2007, 50, 4527–4539. [Google Scholar] [CrossRef]
- Talukdar, P.; Olutmayin, S.O.; Osanyintola, O.F.; Simonson, C.J. An experimental data set for benchmarking 1-D, transient heat and moisture transfer models of hygroscopic building materials. Part II: Experimental, numerical and analytical data. Int. J. Heat Mass Transf. 2007, 50, 4915–4926. [Google Scholar] [CrossRef]
- Teasdale-St-Hilaire, A.; Derome, D. Comparison of experimental and numerical results of wood-frame wall assemblies wetted by simulated wind-driven rain infiltration. Energy Build. 2007, 39, 1131–1139. [Google Scholar] [CrossRef]
- Li, Q.; Rao, J.; Fazio, P. Development of HAM tool for building envelope analysis. Build. Environ. 2009, 44, 1065–1073. [Google Scholar] [CrossRef]
- Piot, A.; Woloszyn, M.; Brau, J.; Abele, C. Experimental wooden frame house for the validation of whole building heat and moisture transfer numerical models. Energy Build. 2011, 43, 1322–1328. [Google Scholar] [CrossRef]
- Desta, T.Z.; Langmans, J.; Roels, S. Experimental data set for validation of heat, air and moisture transport models of building envelopes. Build. Environ. 2011, 46, 1038–1046. [Google Scholar] [CrossRef]
- Langmans, J.; Klein, R.; Roels, S. Numerical and experimental investigation of the hygrothermal response of timber frame walls with an exterior air barrier. J. Build. Phys. 2013, 36, 375–397. [Google Scholar] [CrossRef]
- Rafidiarison, H.; Remond, R.; Mougel, E. Dataset for validating 1-D heat and mass transfer models within building walls with hygroscopic materials. Build. Environ. 2015, 89, 356–368. [Google Scholar] [CrossRef]
- Latif, E.; Ciupala, M.A.; Tucker, S.; Wijeyesekera, D.C.; Newport, D.J. Hygrothermal performance of wood-hemp insulation in timber frame wall panels with and without a vapour barrier. Build. Environ. 2015, 92, 122–134. [Google Scholar] [CrossRef] [Green Version]
- Woloszyn, M.; Le Pierrès, N.; Kedowidé, Y.; Virgone, J.; Trabelsi, A.; Slimani, Z.; Pierre, F. Vers une méthode de conception HYGRO-thermique des BATiments performants: Démarche du projet HYGRO-BAT. In Les Modèles Face aux Résultats Expérimentaux; IBPSA France: Arras, France, 2014; p. 8. [Google Scholar]
- HYGRO-BAT. Livrable de la Tâche 1: Caractérisation de la Métrologie et des Matériaux; ANR-10-HABISOL-005-01; ANR: France, 2015. [Google Scholar]
- ISO 12571. Hygrothermal Performance of Building Materials and Products—Determination of Hygroscopic Sorption Properties; International Organization for Standardization: Geneva, Switzerland, 2013. [Google Scholar]
- Traoré, I. Transferts de Chaleur et de Masse Dans les Parois des Bâtiments à Ossature Bois. Ph.D. Thesis, Henri Poincaré University, Nancy, France, 2011. [Google Scholar]
- Slimani, Z. Analyse Expérimentale et Numérique du Comportement Hygrothermique de Parois Fortement Hygroscopiques. Ph.D. Thesis, Université Claude Bernard Lyon, Villeurbanne, France, 2015. [Google Scholar]
- Zakaria, S.; Abdelkrim, T.; Joseph, V. Study of hygrothermal behavior of very hygroscopic insulation. In Materials, Systems and Structures in Civil. Engineering Conference segment on Moisture in Materials and Structures; Technical University of Denmark: Lyngby, Denmark, 2016. [Google Scholar]
- Luikov, A.V. Heat and Mass Transfer in Capillary-Porous Bodies, 1st ed.; Oxford Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Quenard, D. Adsorption et Transfert D’humidité Dans les Matériaux Hygroscopiques, Approche du Type Percolation et Expérimentation. Ph.D. Thesis, Institut National Polytechnique de Toulouse, Toulose, France, 1989. [Google Scholar]
- Hagentoft, C.E.; Kalagasidis, A.S.; Adl-Zarrabi, B.; Roels, S.; Carmeliet, J.; Hens, H.; Adan, O. Assessment method of numerical prediction models for combined heat, air and moisture transfer in building Components: Benchmarks for one-dimensional cases. J. Therm. Envel. Build. Sci. 2004, 27, 327–352. [Google Scholar] [CrossRef]
- Qin, M.; Belarbi, R.; Aït-Mokhtar, A.; Nilsson, L.O. Coupled heat and moisture transport in multi-layer walls: Numerical simulation and experimental study. Constr. Build. Mater. 2006, 23, 967–975. [Google Scholar] [CrossRef]
- Trabelsi, A. Études Numérique et Expérimentale des Transferts Hygrothermiques Dans les Matériaux Poreux de Construction. Ph.D. Thesis, University of La Rochelle, La Rochelle, France, 2010. [Google Scholar]
- Tariku, F.; Kumaran, K.; Fazio, P. Transient model for coupled heat, air and moisture transfer through multilayered porous media. Int. J. Heat Mass Trans. 2010, 53, 3035–3044. [Google Scholar] [CrossRef] [Green Version]
- Trabelsi, A.; Slimani, Z.; Virgone, J. Response surface analysis of the dimensionless heat and mass transfer parameters of medium density fiberboard. Int. J. Heat Mass Trans. 2018, 127, 623–630. [Google Scholar] [CrossRef]










| RH (%) | 0 | 15 | 22.5 | 30 | 43 | 45 | 60 | 66 | 75 | 90 | 93 | 97 |
| USorption | 0.00 | 3.10 | 4.10 | 4.88 | 6.06 | 6.25 | 8.08 | 9.14 | 11.27 | 16.70 | 18.14 | 20.26 |
| UDesorption | 0.00 | 3.60 | 4.74 | 5.61 | 6.81 | 6.99 | 8.73 | 9.74 | 11.79 | 17.15 | 18.58 | 20.70 |
| UMean | 0.00 | 3.35 | 4.42 | 5.25 | 6.43 | 6.62 | 8.40 | 9.44 | 11.53 | 16.92 | 18.36 | 20.48 |
| SD | - | 0.86 | 0.86 | 0.87 | 0.89 | 0.89 | 0.93 | 0.94 | 0.96 | 0.97 | 0.98 | 0.98 |
| Hygrothermal Property (unit) | Value |
|---|---|
| Apparent density (kg/m3) | 146 |
| Porosity (%) | 90–99 |
| Water vapor resistance coefficients (-) | 2.73 |
| Thermal conductivity (W/(m·K)) | |
| Specific heat (J/(kg·K)) |
| Measurement | Domain | Uncertainty |
|---|---|---|
| Temperature (SHT75) | 5–45 °C | 0.17 °C |
| Relative humidity (SHT75) | 40–90% | 2% |
| Temperature (Pt100) | 5–45 °C | 0.15 °C |
| Temperature (thermocouples) | 5–45 °C | 0.16 °C |
| State Variable | Interior Air | Exterior Air |
|---|---|---|
| T (°C) | 19 | 5 |
| RH (%) | 55 | 88 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slimani, Z.; Trabelsi, A.; Virgone, J.; Zanetti Freire, R. Study of the Hygrothermal Behavior of Wood Fiber Insulation Subjected to Non-Isothermal Loading. Appl. Sci. 2019, 9, 2359. https://doi.org/10.3390/app9112359
Slimani Z, Trabelsi A, Virgone J, Zanetti Freire R. Study of the Hygrothermal Behavior of Wood Fiber Insulation Subjected to Non-Isothermal Loading. Applied Sciences. 2019; 9(11):2359. https://doi.org/10.3390/app9112359
Chicago/Turabian StyleSlimani, Zakaria, Abdelkrim Trabelsi, Joseph Virgone, and Roberto Zanetti Freire. 2019. "Study of the Hygrothermal Behavior of Wood Fiber Insulation Subjected to Non-Isothermal Loading" Applied Sciences 9, no. 11: 2359. https://doi.org/10.3390/app9112359
APA StyleSlimani, Z., Trabelsi, A., Virgone, J., & Zanetti Freire, R. (2019). Study of the Hygrothermal Behavior of Wood Fiber Insulation Subjected to Non-Isothermal Loading. Applied Sciences, 9(11), 2359. https://doi.org/10.3390/app9112359





