Numerical–Experimental Correlation of Impact-Induced Damages in CFRP Laminates
Abstract
:Featured Application
Abstract
1. Introduction
2. Theoretical background
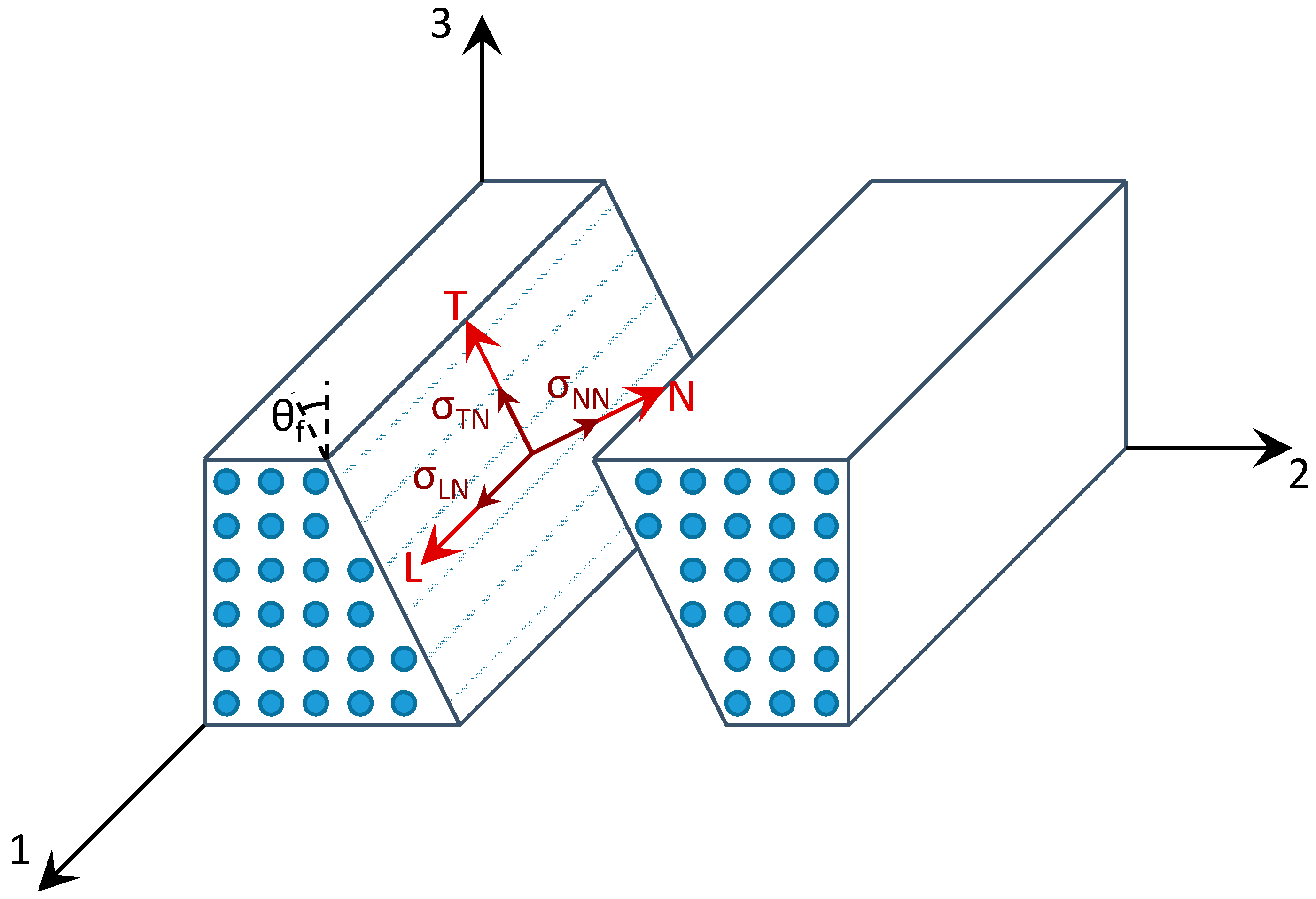
2.1. Classical Laminated Plate Theory
2.2. Composites Damage Criteria
3. Test Cases Descriptions
3.1. Analytical Set-Up
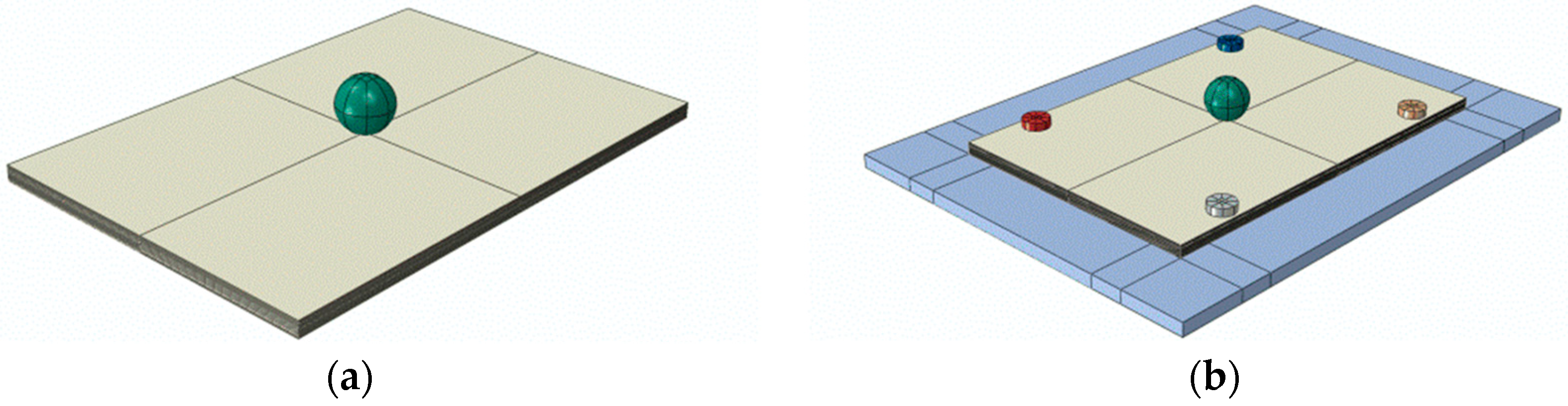
3.2. Experimental Set-Up
4. Results and Discussion
4.1. Preliminary Analyses
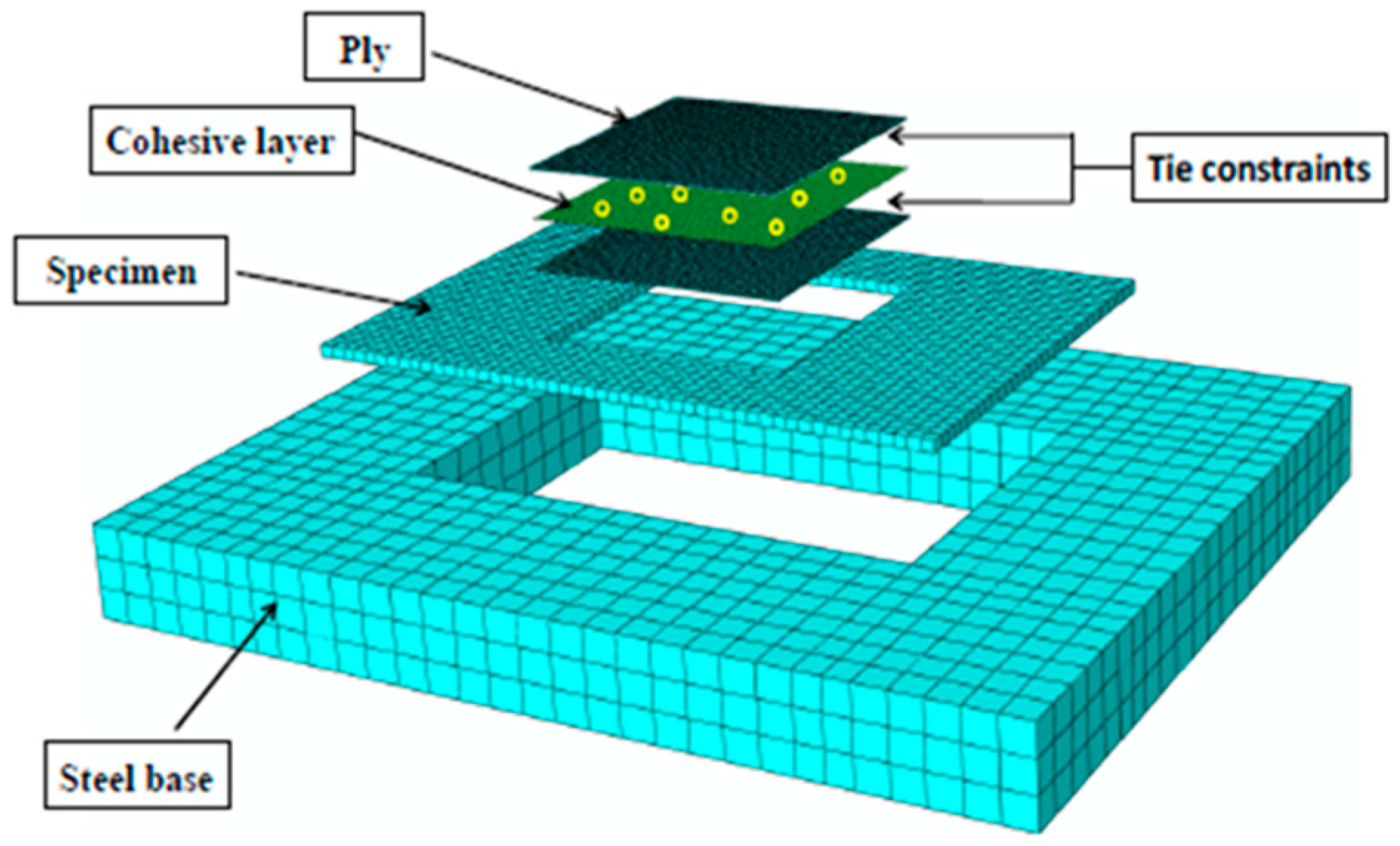
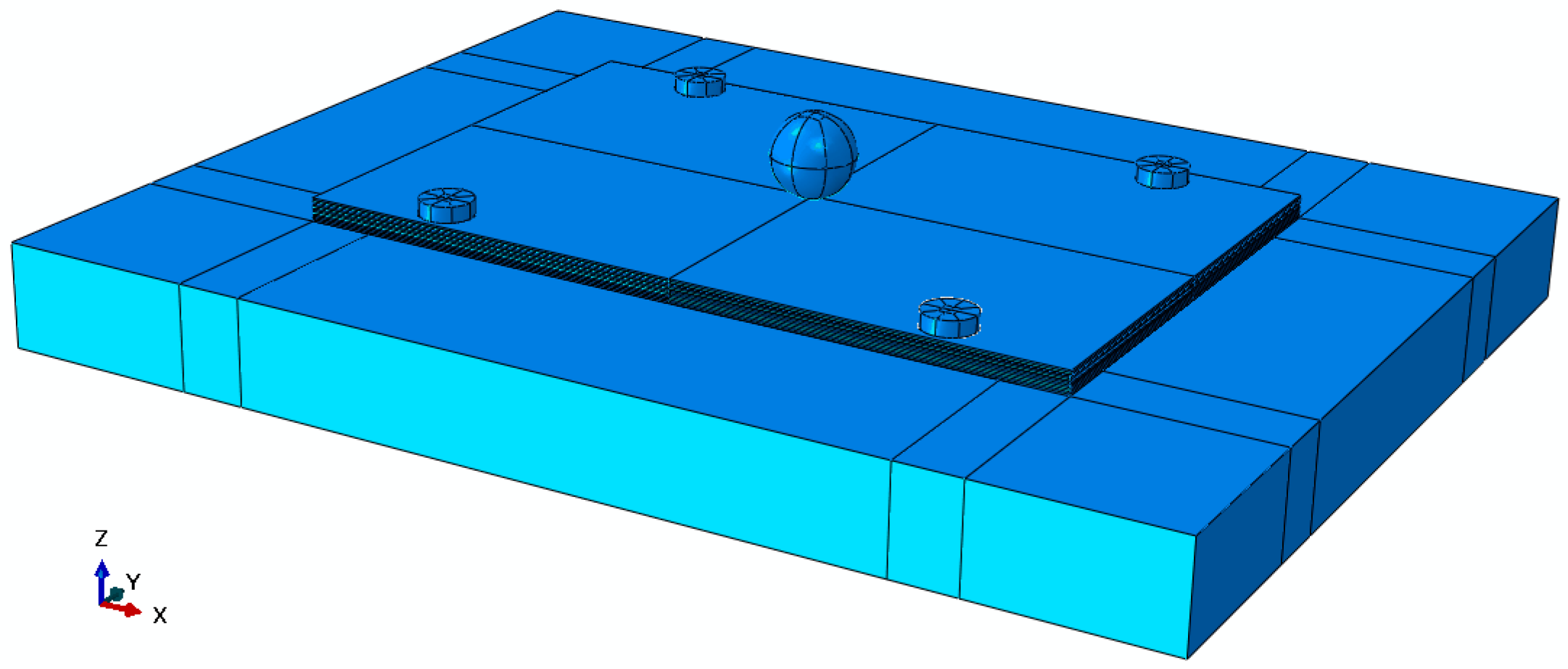
4.2. Final Solid Model
4.3. Final Continuum Shell Model
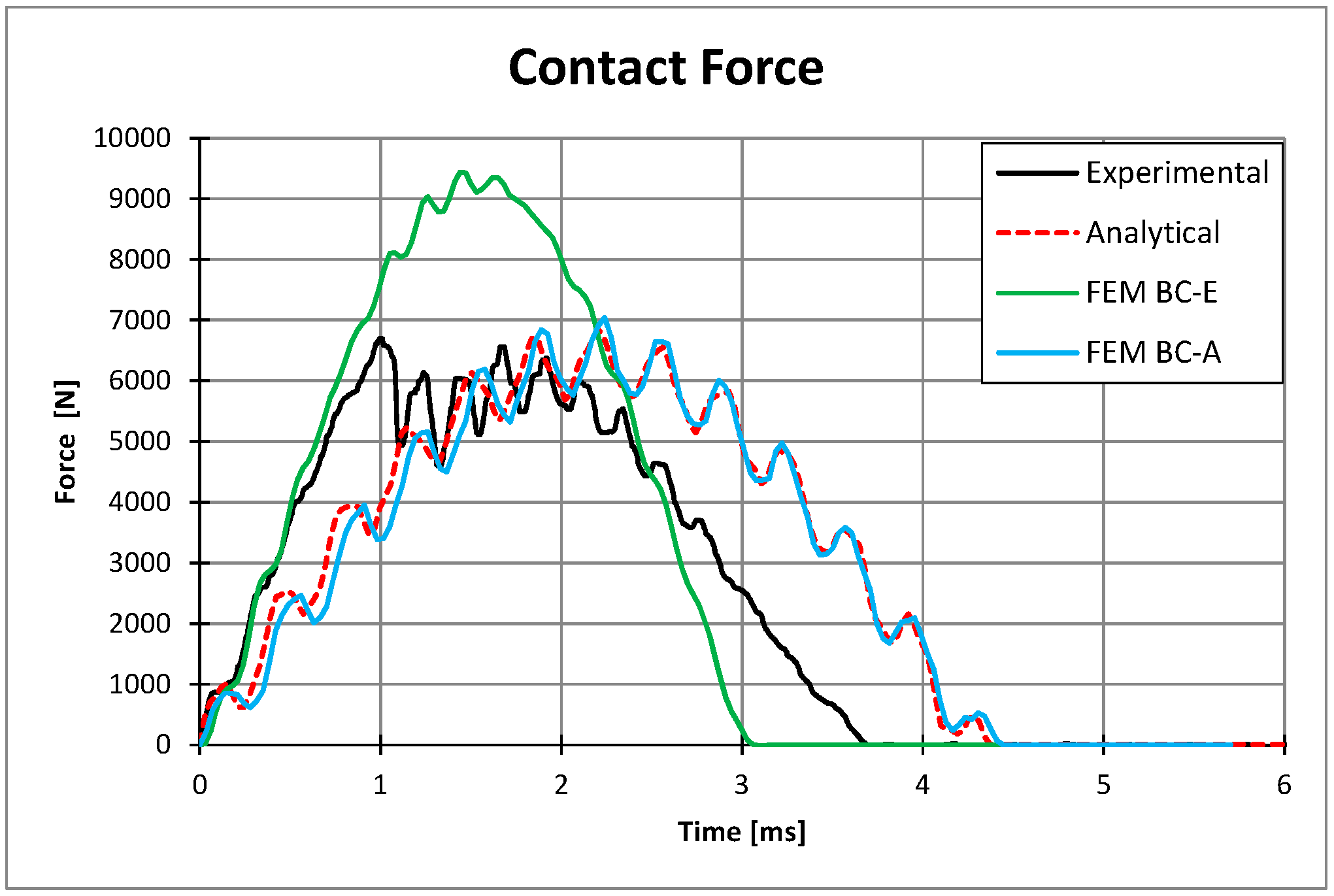
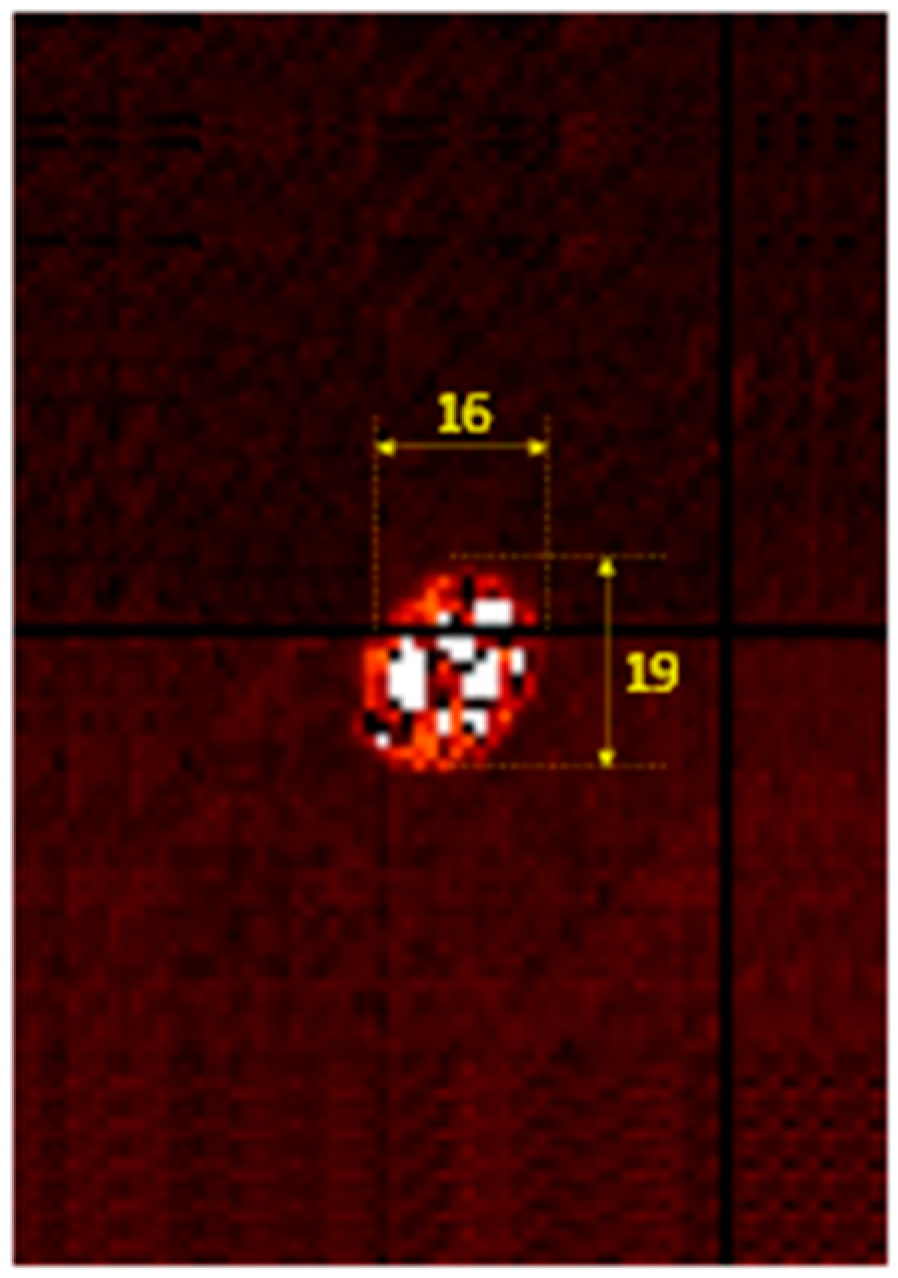
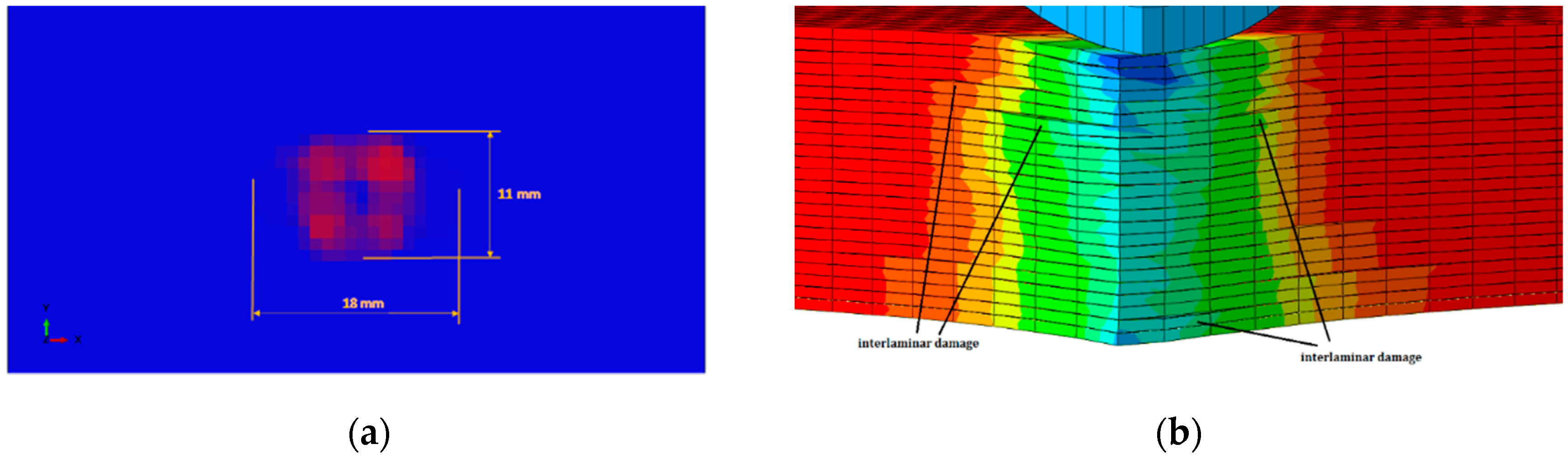
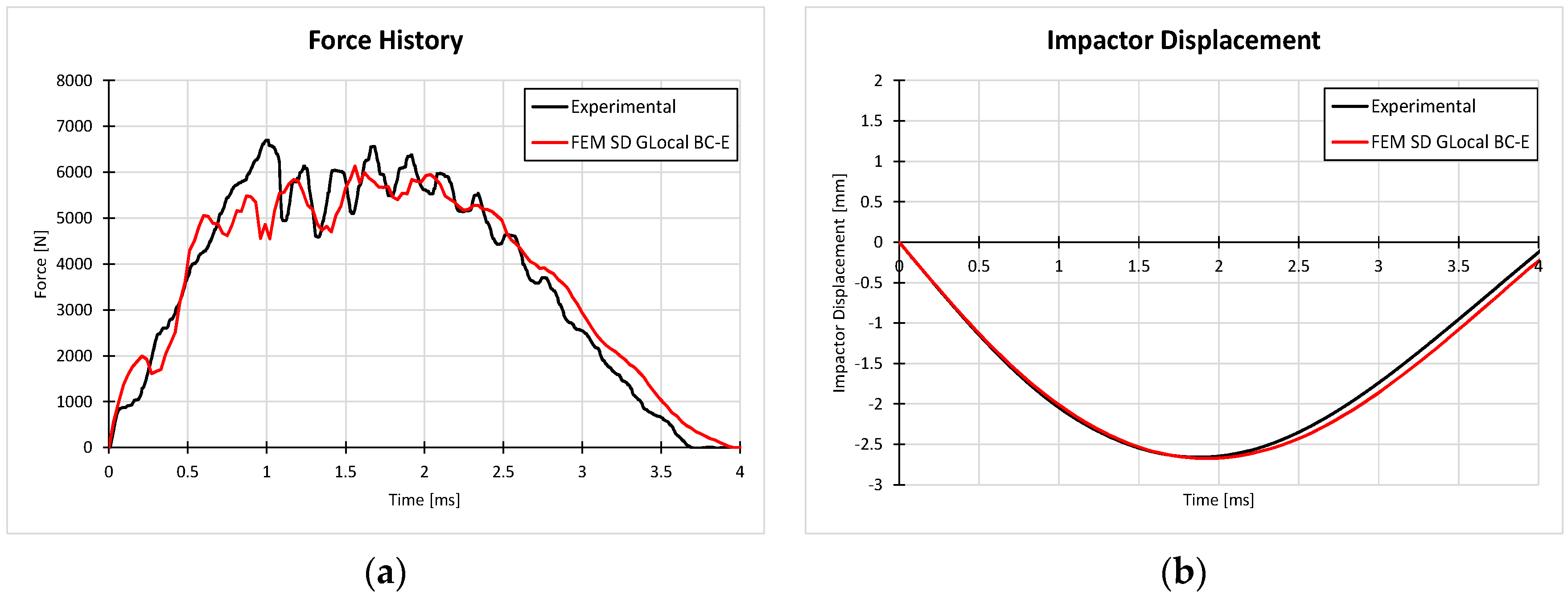
4.4. Numerical–Experimental Correlation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abrate, S. Impact on Composite Structures; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Abrate, S. Impact Engineering of Composites Structures; Springer: Wien, Austria; Udine, Italy, 2011. [Google Scholar]
- Zhang, X. Low Velocity Impact and Damage Tolerance of Composite Aircraft Structures; Cranfield University: Cranfield, UK, 2003. [Google Scholar]
- Soutis, C.; Curtis, P. Prediction of the post-impact compressive strength of CFRP laminated composites. Compos. Sci. Technol. 1996, 56, 677–684. [Google Scholar] [CrossRef]
- Wisnom, M. The role of delamination in failure of fibre-reinforced composites. Philos. Trans. R. Soc. 2012, 370, 1850–1870. [Google Scholar] [CrossRef] [PubMed]
- Abrate, S. Modeling of impacts on composite structures. Compos. Struct. 2001, 51, 129–138. [Google Scholar] [CrossRef]
- Christoforou, A.; Swanson, S. Analysis of impact response in composite plates. Int. J. Solid Struct. 1991, 27, 161–170. [Google Scholar] [CrossRef]
- Carvalho, A.; Guedes Soares, C. Dynamic response of rectangular plates of composite materials subjected to impact loads. Compos. Struct. 1996, 34, 55–63. [Google Scholar] [CrossRef]
- Gonzàlez, E.; Maimì, P.; Camanho, P.; Turon, A.; Mayugo, J. Simulation of drop-weight impact and compression after impact tests on composite laminates. Compos. Struct. 2012, 94, 3364–3378. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Vimalathithan, P.K. Acousto-ultrasonic evaluation of interlaminar strength on CFRP laminates. Compos. Struct. 2019, 208, 796–805. [Google Scholar] [CrossRef]
- Olsson, R. Analytical prediction of large mass impact damage in composite laminates. Compos.-Part A Appl. Sci. Manuf. 2001, 32, 1207–1215. [Google Scholar] [CrossRef]
- Olsson, R. Closed form prediction of peak load and delamination onset under small mass impact. Compos. Struct. 2003, 59, 341–349. [Google Scholar] [CrossRef]
- Olsson, R. Analytical prediction of damage due to large mass impact on thin ply composites. Compos.-Part A Appl. Sci. Manuf. 2015, 72, 184–191. [Google Scholar] [CrossRef]
- Huang, K.Y.; De Boer, A.; Akkerman, R. Analytical modeling of impact resistance and damage tolerance of laminated composite plates. AIAA J. 2008, 46, 2760–2772. [Google Scholar] [CrossRef]
- Tita, V.; deCarvalho, J.; Vandepitte, D. Failure analysis of low velocity impact on thin composite laminates: Experimental and numerical approaches. Compos. Struct. 2008, 83, 413–428. [Google Scholar] [CrossRef]
- Li, C.; Hu, N.; Yin, Y.; Sekine, H.; Fukunaga, H. Low-velocity impact-induced damage of continuous fiber-reinforced composite laminates. Part I: An FEM numerical model. Composites 2002, 33, 1055–1062. [Google Scholar] [CrossRef]
- Elder, D.; Thomson, R.; Nguyen, M.; Scott, M. Review of delamination predictive methods for low speed impact of composite laminates. Compos. Struct. 2004, 66, 677–683. [Google Scholar] [CrossRef]
- Riccio, A.; Caputo, F.; Di Felice, G.; Saputo, S.; Toscano, C.; Lopresto, V. A Joint Numerical-Experimental Study on Impact Induced Intra-laminar and Inter-laminar Damage in Laminated Composites. Appl. Compos. Mater. 2016, 23, 219–237. [Google Scholar] [CrossRef]
- Riccio, A.; Raimondo, A.; Saputo, S.; Sellitto, A.; Battaglia, M.; Petrone, G. A numerical study on the impact behavior of natural fibres made honeycomb cores. Compos. Struct. 2018, 202, 909–916. [Google Scholar] [CrossRef]
- Li, N.; Chen, P.H. Micro–macro FE modeling of damage evolution in laminated composite plates subjected to low velocity impact. Compos. Struct. 2016, 147, 111–121. [Google Scholar] [CrossRef]
- Faggiani, A.; Falzon, B.G. Predicting low-velocity impact damage on a stiffened composite panel. Compos.-Part A Appl. Sci. Manuf. 2010, 41, 737–749. [Google Scholar] [CrossRef]
- Falzon, B.G.; Apruzzese, P. Numerical analysis of intralaminar failure mechanisms in composite structures. Part I: FE implementation. Compos. Struct. 2011, 93, 1039–1046. [Google Scholar] [CrossRef]
- Falzon, B.G.; Apruzzese, P. Numerical analysis of intralaminar failure mechanisms in composite structures. Part II: Applications. Compos. Struct. 2011, 93, 1047–1053. [Google Scholar] [CrossRef]
- Tay, T. Characterization and analysis of delamination fracture in composites: An overview of developments from 1990 to 2001. Appl. Mech. Rev. 2003, 56, 1–32. [Google Scholar] [CrossRef]
- Wisnom, M. Modeling discrete failures in composites with interface elements. Compos. Part A 2010, 41, 795–805. [Google Scholar] [CrossRef]
- Camanho, P.; Davila, C. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials; NASA/TM-2002-211737; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 2002; pp. 1–37. [Google Scholar]
- Riccio, A.; Russo, A.; Sellitto, A.; Raimondo, A. Development and application of a numerical procedure for the simulation of the “Fibre Bridging” phenomenon in composite structures. Compos. Struct. 2017, 168, 104–119. [Google Scholar] [CrossRef]
- Riccio, A.; Ricchiuto, R.; Di Caprio, F.; Sellitto, A.; Raimondo, A. Numerical investigation of constitutive material models on bonded joints in scarf repaired composite laminates. Eng. Fract. Mech. 2017, 173, 91–106. [Google Scholar] [CrossRef]
- Aymerich, F.; Dore, F.; Priolo, P. Simulation of multiple delaminations in impacted cross-ply laminates using a finite element model based on cohesive interface elements. Compos. Sci. Technol. 2009, 69, 1699–1709. [Google Scholar] [CrossRef]
- DeMoura, M.; Gonçalves, J. Modeling the interaction between matrix cracking and delamination in carbon–epoxy laminates under low velocity impact. Compos. Sci. Technol. 2004, 64, 1021–1027. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, P.; Lai, X. Finite element analysis of low-velocity impact damage in composite laminated plates. Mater. Des. 2006, 27, 513–519. [Google Scholar] [CrossRef]
- deBorst, R.; Remmers, J.J.; Needleman, A. Mesh-independent discrete numerical representations of cohesive-zone models. Eng. Fract. Mech. 2006, 73, 160–177. [Google Scholar]
- Maimì, P.; Camanho, P.; Mayugo, J.; Davila, C. A continuum damage model for composite laminates: Part I—Constitutive model. Mech. Mater. 2007, 39, 897–908. [Google Scholar] [CrossRef]
- ASTM D7136/D-Standard Test Method for Measuring the Damage Resistance of a Fiber-Reinforced Polymer Matrix Composite to a Drop-Weight Impact Event; ASTM International: West Conshohocken, PA, USA, 2005.
- Sellitto, A.; Borrelli, R.; Caputo, F.; Riccio, A.; Scaramuzzino, F. Application to plate components of a kinematic global-local approach for non-matching finite element meshes. Int. J. Struct. Integr. 2012, 3, 260–273. [Google Scholar] [CrossRef]
- Dassault System Abaqus 2016 User’s Manual; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2016.
- Christoforou, A.; Yigit, A. Effect of flexibility on low velocity impact response. J. Sound Vib. 1998, 217, 563–578. [Google Scholar] [CrossRef]
- Puck, A.; Schurmann, H. Failure analysis of FRP laminates by means of physically based phenomenological models. Compos. Sci. Technol. 1998, 58, 1045–1067. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Mater. Struct. 1983, 16, 155–177. [Google Scholar] [Green Version]
- Davies, G.A.O.; Olsson, R. Impact on composite structures. Aeronaut. J. 2004, 108, 541–563. [Google Scholar] [CrossRef]





















| Property [unit] | Value |
|---|---|
| ρ [kg/m3] | 1600 |
| E11 [MPa] | 149,500 |
| E22 = E33 [MPa] | 8430 |
| G12 = G13 [MPa] | 4200 |
| G23 [MPa] | 2520 |
| υ12 = υ13 [-] | 0.3 |
| υ23 [-] | 0.45 |
| υ21 [-] | 0.0186 |
| XT [MPa] | 2143 |
| XC [MPa] | 1034 |
| YT [MPa] | 75 |
| YC [MPa] | 250 |
| S12 = S13 [MPa] | 108 |
| S23 [MPa] | 95 |
| GT1c [kJ/m2] | 30.72 |
| GC1c [kJ/m2] | 7.15 |
| GT2c [kJ/m2] | 0.667 |
| GC2c [kJ/m2] | 7.41 |
| Ply thickness [mm] | 0.186 |
| Property [unit] | Value |
|---|---|
| En [MPa/mm] | 1.155 × 106 |
| Et [MPa/mm] | 6 × 105 |
| Es [MPa/mm] | 6 × 105 |
| Nmax [MPa] | 62.3 |
| Tmax [MPa] | 92.3 |
| Smax [MPa] | 92.3 |
| GIc [kJ/m2] | 0.18 |
| GIIc [kJ/m2] | 0.5 |
| GIIIc [kJ/m2] | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sellitto, A.; Saputo, S.; Di Caprio, F.; Riccio, A.; Russo, A.; Acanfora, V. Numerical–Experimental Correlation of Impact-Induced Damages in CFRP Laminates. Appl. Sci. 2019, 9, 2372. https://doi.org/10.3390/app9112372
Sellitto A, Saputo S, Di Caprio F, Riccio A, Russo A, Acanfora V. Numerical–Experimental Correlation of Impact-Induced Damages in CFRP Laminates. Applied Sciences. 2019; 9(11):2372. https://doi.org/10.3390/app9112372
Chicago/Turabian StyleSellitto, Andrea, Salvatore Saputo, Francesco Di Caprio, Aniello Riccio, Angela Russo, and Valerio Acanfora. 2019. "Numerical–Experimental Correlation of Impact-Induced Damages in CFRP Laminates" Applied Sciences 9, no. 11: 2372. https://doi.org/10.3390/app9112372
APA StyleSellitto, A., Saputo, S., Di Caprio, F., Riccio, A., Russo, A., & Acanfora, V. (2019). Numerical–Experimental Correlation of Impact-Induced Damages in CFRP Laminates. Applied Sciences, 9(11), 2372. https://doi.org/10.3390/app9112372









