Auto-Generation System Based on Fractal Geometry for Batik Pattern Design
Abstract
:Featured Application
Abstract
1. Introduction
2. Related Work
2.1. Fractal Geometry
- Self-similarity, which may include precise self-similarity—the same at all scales; quasi-self-similarity—similar patterns on different scales, where small copies of the entire fractal may contain distorted and degenerate forms; statistical self-similarity—random repetition of a pattern so that a number or statistical measurement remains across scales [7]; qualitative self-similarity—such as time series [8]; or multifractal scaling [9,10,11,12]—represented by multiple fractal dimensions or scaling rules.
- Fine or detailed structure on any small scale. The result of this structure is that fractals may have emergent properties [13].
- Local and global irregularities are not easily described in traditional Euclidean geometric languages. For images of fractal patterns, this has been expressed by phrases such as “smoothly stacked surfaces” and “whirlpools on vortices” [14].
- Strange attractors—use iterations of a map or solutions of a system of initial-value differential or difference equations that exhibit chaos.
- Escape-time fractals—use a formula or recurrence relation at each point in a space (such as a complex plane); usually quasi-self-similar; also known as “orbit” fractals.
- Random fractals—use stochastic rules.
2.2. Fractal Pattern Generation
3. Fractal Characteristics of Batik Patterns and Fractal Algorithms
3.1. Fractal Characteristic of Batik Flower Patterns
3.2. Iterated Function System
4. Auto-Generation Algorithm Based on Fractal Geometry
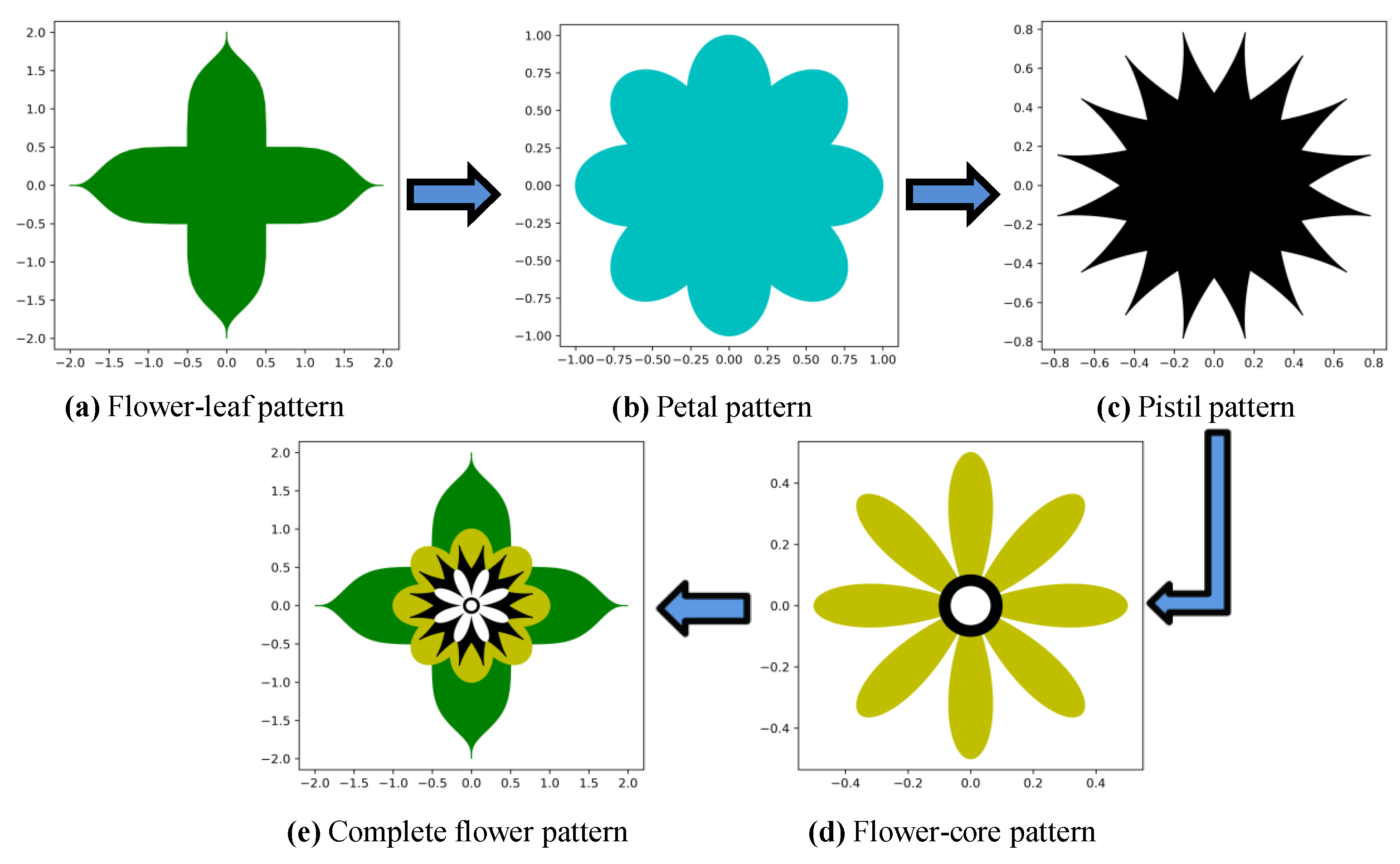
4.1. Generating the Flower-Leaves Pattern
4.2. Generating the Petals Pattern
4.3. Generating the Pistils Pattern
4.4. Generating the Flower-Core Pattern
4.5. Generating the Flower Pattern Layout
5. Experiment and Analysis
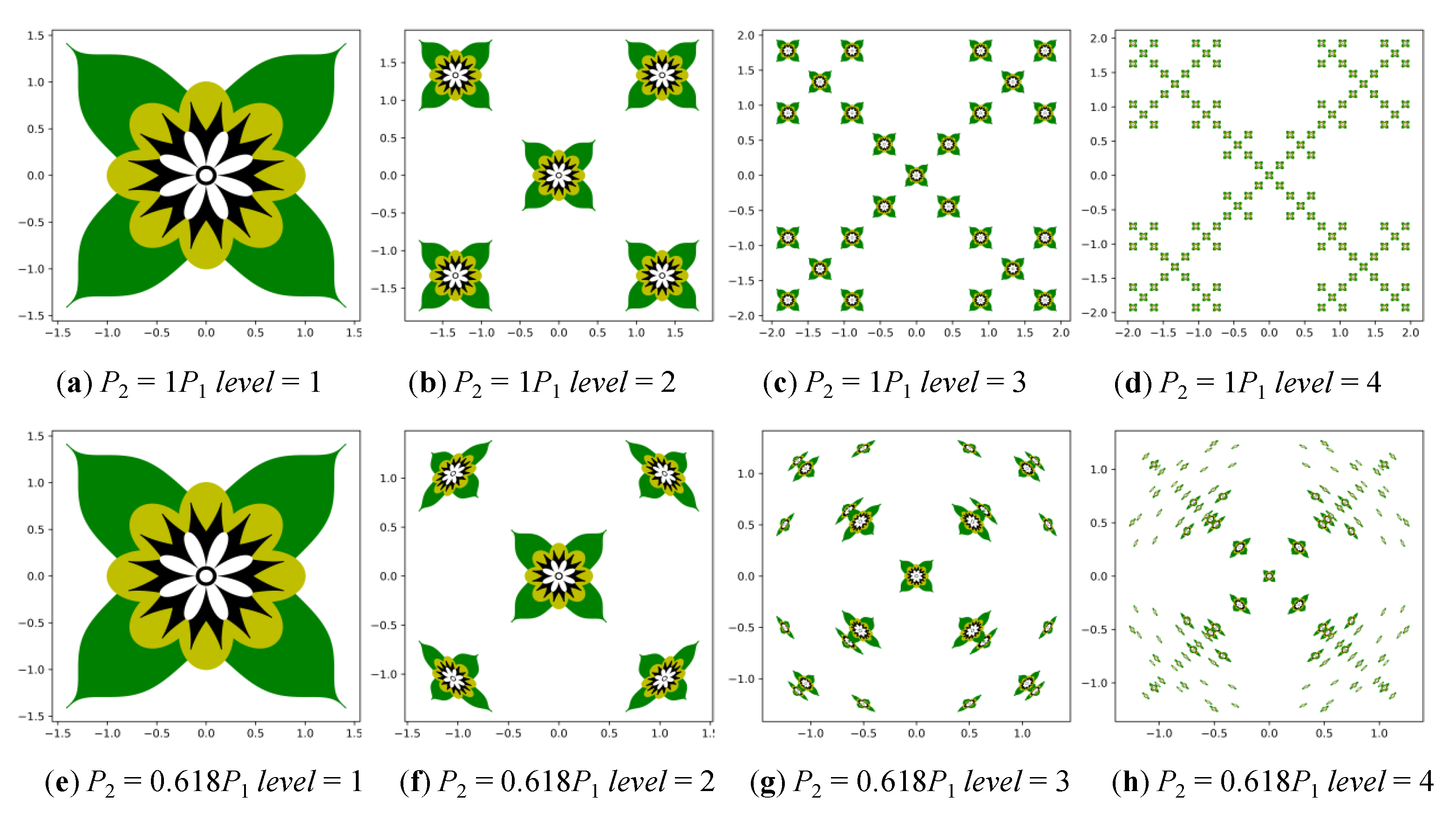
5.1. Setting Parameters to Generate Flower Patterns
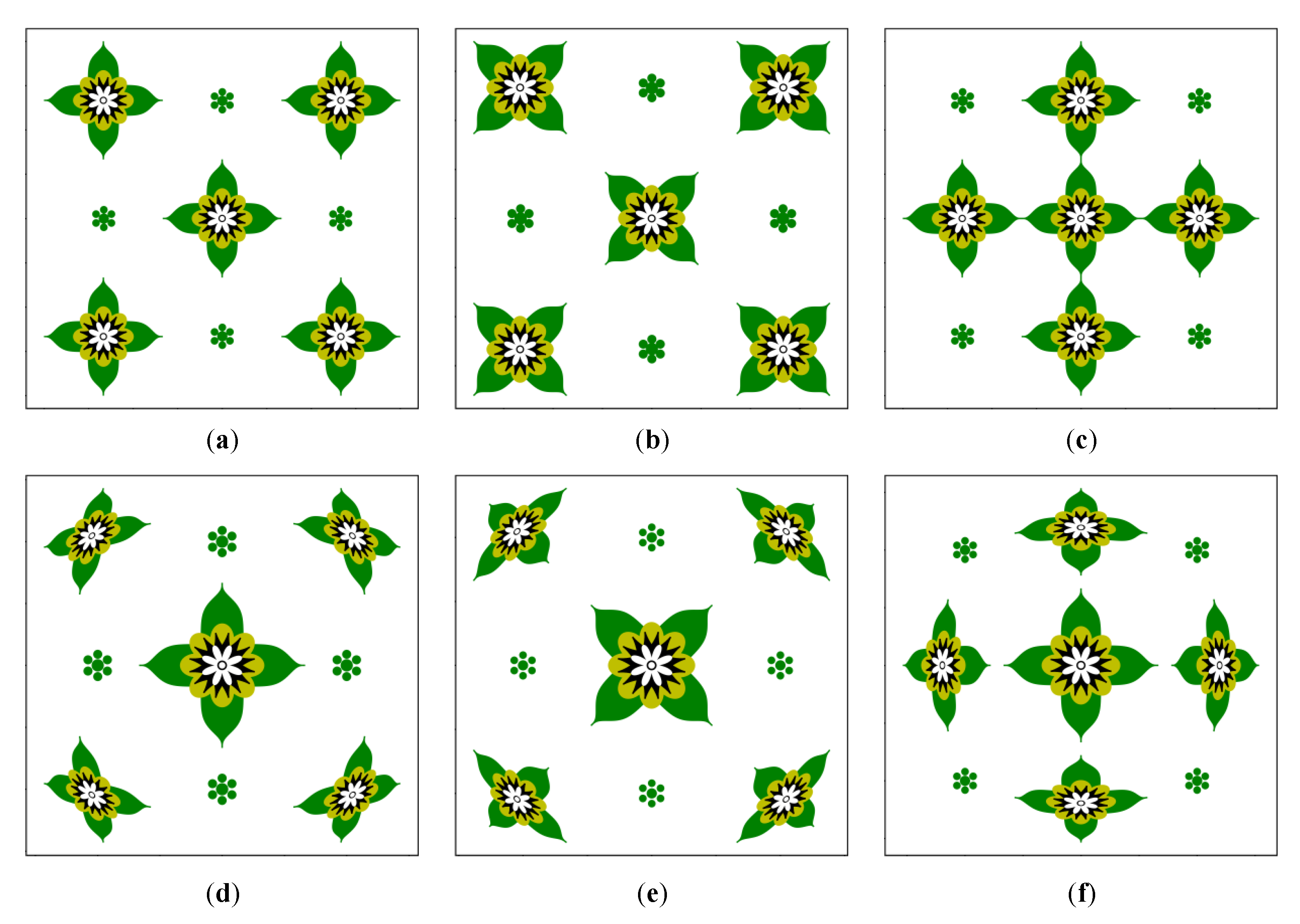
5.2. Setting Parameters to Generate Layout Patterns of Flowers
6. System Implementation
7. Analysis
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, H.; Zhang, C.Y. Comparative study of ethnic groups’ batik patterns in Southwest China. J. Text. Res. 2016, 37, 101–106. [Google Scholar]
- Wang, T.F. Research on Miao Batik Art—Taking the Anshun Area of Guizhou as an Object. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, November 2014. [Google Scholar]
- Zhang, X.H.; Li, H.Y. Production of art patterns based on fractal cloud model cellular automata. J. Tsinghua Univ. (Sci. Technol.) 2013, 53, 1098–1103. [Google Scholar]
- Cui, J.; Tang, M.X. Integrating shape grammars into a generative system for Zhuang ethnic embroidery design exploration. Comput. Aided Des. 2013, 45, 591–604. [Google Scholar] [CrossRef]
- Liu, S.G.; Chen, D. Computer simulation of batik printing patterns with cracks. Text. Res. J. 2015, 85, 1972–1984. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Vicsek, T. Fractal Growth Phenomena; World Scientific Publishing Company: Singapore, 1992. [Google Scholar]
- Peters, E.E. Chaos and Order in the Capital Markets: A New View of Cycles, Prices, and Market Volatility; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Perrier, E.; Tarquis, A.M.; Dathe, A. A program for fractal and multifractal analysis of two-dimensional binary images: Computer algorithms versus mathematical theory. Geoderma 2006, 134, 284–294. [Google Scholar] [CrossRef] [Green Version]
- Ouahabi, A. Signal and Image Multiresolution Analysis; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Djeddi, M.; Ouahabi, A.; Batatia, H.; Basarab, A.; Kouamé, D. Discrete wavelet for multifractal texture classification: Application to medical ultrasound imaging. In Proceedings of the 17th IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 637–640. [Google Scholar]
- Ouahabi, A. Multifractal analysis for texture characterization: A new approach based on DWT. In Proceedings of the 10th International Conference on Information Science, Signal Processing and their Applications, Kuala Lumpur, Malysia, 10–13 May 2010; pp. 698–703. [Google Scholar]
- Corbetta, D.; Spencer, J.P.; Thomas, M.; McClelland, J. Toward a Unified Theory of Development: Connectionism and Dynamic Systems Theory Re-Considered; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Mandelbrot, B.B. A fractal set is one for which the fractal (Hausdorff-Besicovitch) dimension strictly exceeds the topological dimension. Fract. Chaos 2004, 978–1000. [Google Scholar]
- Pickover, C.A. Chaos and Fractals: A Computer Graphical Journey; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Fisher, Y. Fractal Image Compression: Theory and Application; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Jelinek, H.; Karperien, A.; Cornforth, D.; Cesar, R.M.J.; Leandro, J. MicroMod—An L-systems approach to neuron modelling. In Proceedings of the Sixth Australasia-Japan Joint Workshop on Intelligent and Evolutionary Systems, Canberra, Australia, 22–24 November 2002; pp. 156–163. [Google Scholar]
- Hahn, H.K.; Georg, M.; Peitgen, H.O. Fractal Aspects of Three-Dimensional Vascular Constructive Optimization. Fractals in Biology and Medicine; Birkhäuser Basel: Basel, Switzerland, 2005; pp. 55–66. [Google Scholar]
- Cannon, J.; Floyd, W.; Parry, W. Finite subdivision rules. Conform. Geom. Dynam. 2001, 5, 153–196. [Google Scholar] [CrossRef]
- Cannon, J.W.; Floyd, W.J.; Parry, W.R. Crystal Growth, Biological Cell Growth, and Geometry, Pattern Formation in Biology, Vision and Dynamics; Carbone, A., Gromov, M., Prusinkiewicz, P., Eds.; World Scientific Publishing Company: Singapore, 2000. [Google Scholar]
- Hariadi, Y.; Lukman, M.; Destiarmand, A.H. Batik fractal: Marriage of art and science. J. Vis. Art Des. 2013, 4, 84–93. [Google Scholar] [CrossRef]
- Indraprastha, A.; Sahputra, Z.; Suharjono, A. Preserving local ornament through algorithm. J. Ilmu Komput. Dan Inf. 2013, 6, 52–58. [Google Scholar]
- Riwansia, R.R. Pengembangan Desain Batik melalui Penggunaan Geometri Fraktal Koch Snowflake. Pros. Semin. Jember Univ. Jember 2016. [Google Scholar]
- Purnomo, K.D. Pembangkitan Segitiga Sierpinski dengan Transformasi Affine Berbasis Beberapa Benda Geometris. Prosiding Seminar Nasional Matematika. pp. 41–48. Available online: https://jurnal.unej.ac.id/index.php/psmp/article/view/977 (accessed on 19 December 2014).
- Romadiastri, Y. Batik Fraktal: Perkembangan Aplikasi Geometri Fraktal. Delta: J. Ilm. Pendidik. Matematika 2017, 1, 158–164. [Google Scholar]
- Muhamad, L.; Nancy, M.; Yun, H.P. Pixel People Project. Available online: http: //jbatik.com (accessed on 18 February 2019).
- Zhang, D.Y.; Chen, L.; Wang, H.J. Application of deterministic L-systems in knitting pattern design. J. Text. Res. 2015, 36, 35–38. [Google Scholar]
- Yuan, Q.N.; Lv, J.; Huang, H.S. Auto-Generation Method of Butterfly Pattern of Batik Based on Fractal Geometry. Int. J. Signal Process. Image Process. Pattern Recognit. 2016, 9, 369–392. [Google Scholar] [CrossRef]
- Zhang, X.W.; Wang, J.; Lu, G.D.; Fei, S.M.; Zhang, D.L. Extraction and reuse of pattern configuration based on ontology and shape grammar. J. ZheJiang Univ. (Eng. Sci.) 2018, 52, 461–472. [Google Scholar]
- Yuan, H.F.; Cheng, W.Y.; Wang, X.; Liu, X.H. Fractal pattern design based on Kronecker product and the application in Wangjiang cross stitch. J. Donghua Univ. (Nat. Sci.) 2017, 43, 651–654. [Google Scholar]
- Wang, S.H.; Yang, X.H. Generation of fractal image on complex plane and its application in textiles. J. Silk 2017, 54, 56–61. [Google Scholar]
- Lu, L.S.; Song, X.X. Application of fractal pattern in computer jacquard knitted fabric. J. Silk 2017, 54, 25–29. [Google Scholar]
- Falconer, K.J. Techniques in Fractal Geometry; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- Dura, E.; Bell, J.; Lane, D. Superellipse Fitting for the Recovery and Classification of Mine-Like Shapes in Sidescan Sonar Images. IEEE J. Oceanic Eng. 2008, 33, 434–444. [Google Scholar] [CrossRef]
- Basieux, P. Abenteuer Mathematik: Brücken zwischen Wirklichkeit und Fiktion; Springer: Berlin, Germany, 2012. [Google Scholar]
- Wußing, H. 6000 Jahre Mathematik: Von den Anfängen bis Leibniz und Newton; Springer Spektrum: Berlin, Deutschland, 2013. [Google Scholar]













| Basic Features | Evaluation Parameter |
|---|---|
| Elements number | 1, 2, 3, multi |
| Positional relationship | Rotation, translation |
| Symmetry | None, 1/2, 1/3, 1/4, …, rotation |
| Petals layers number | Single, double, multi |
| Petal shape | Rhombus, curved, wavy |
| Petals number/layer | 6, 7, 8, 9, 10, or more |
| Pistils number/petal | None, 1, 2, multi |
| Flower Pattern | Generation | Original |
|---|---|---|
| Flower 1 | 2, rotation, 1/8, single, curved, 8, 1 | 2, rotation, 1/8, single, curved, 8, 1 |
| Flower 2 | 3, rotation, 1/8, single, wavy, 8, 2 | 3, rotation, 1/8, single, wavy, 8, 2 |
| Flower 3 | 2, rotation, 1/8, single, rhombus, 8, 2 | 2, rotation, 1/8, single, rhombus, 8, 2 |
| Flower 4 | 2, rotation, 1/6, double, curved, 6, 2, | 2, rotation, 1/6, double, curved, 6 and 12, 4 and 5 |
| Flower 5 | 2, rotation, 1/8, single, curved, 8, multi | 2, rotation, 1/8, single, curved, 8, multi |
| Flower 6 | 2, rotation, none, multi, curved, 10 or more, none | 2, rotation, 1/3, multi, curved, 10 or more, none |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, G.; Yuan, Q.; Hu, T.; Shi, Y. Auto-Generation System Based on Fractal Geometry for Batik Pattern Design. Appl. Sci. 2019, 9, 2383. https://doi.org/10.3390/app9112383
Tian G, Yuan Q, Hu T, Shi Y. Auto-Generation System Based on Fractal Geometry for Batik Pattern Design. Applied Sciences. 2019; 9(11):2383. https://doi.org/10.3390/app9112383
Chicago/Turabian StyleTian, Guidong, Qingni Yuan, Tao Hu, and Yi Shi. 2019. "Auto-Generation System Based on Fractal Geometry for Batik Pattern Design" Applied Sciences 9, no. 11: 2383. https://doi.org/10.3390/app9112383
APA StyleTian, G., Yuan, Q., Hu, T., & Shi, Y. (2019). Auto-Generation System Based on Fractal Geometry for Batik Pattern Design. Applied Sciences, 9(11), 2383. https://doi.org/10.3390/app9112383




