A Super-Harmonic Feature Based Updating Method for Crack Identification in Rotors Using a Kriging Surrogate Model
Abstract
:1. Introduction
2. Modelling and Validation of a Two-Disc Rotor with a Breathing Crack
3. Investigation of the Effects of Crack Parameters on Super-Harmonic Characteristics
4. Construction of the Crack Kriging Surrogate Model
5. Crack Identification Method Based on the Kriging Surrogate Model
6. Numerical Experiments
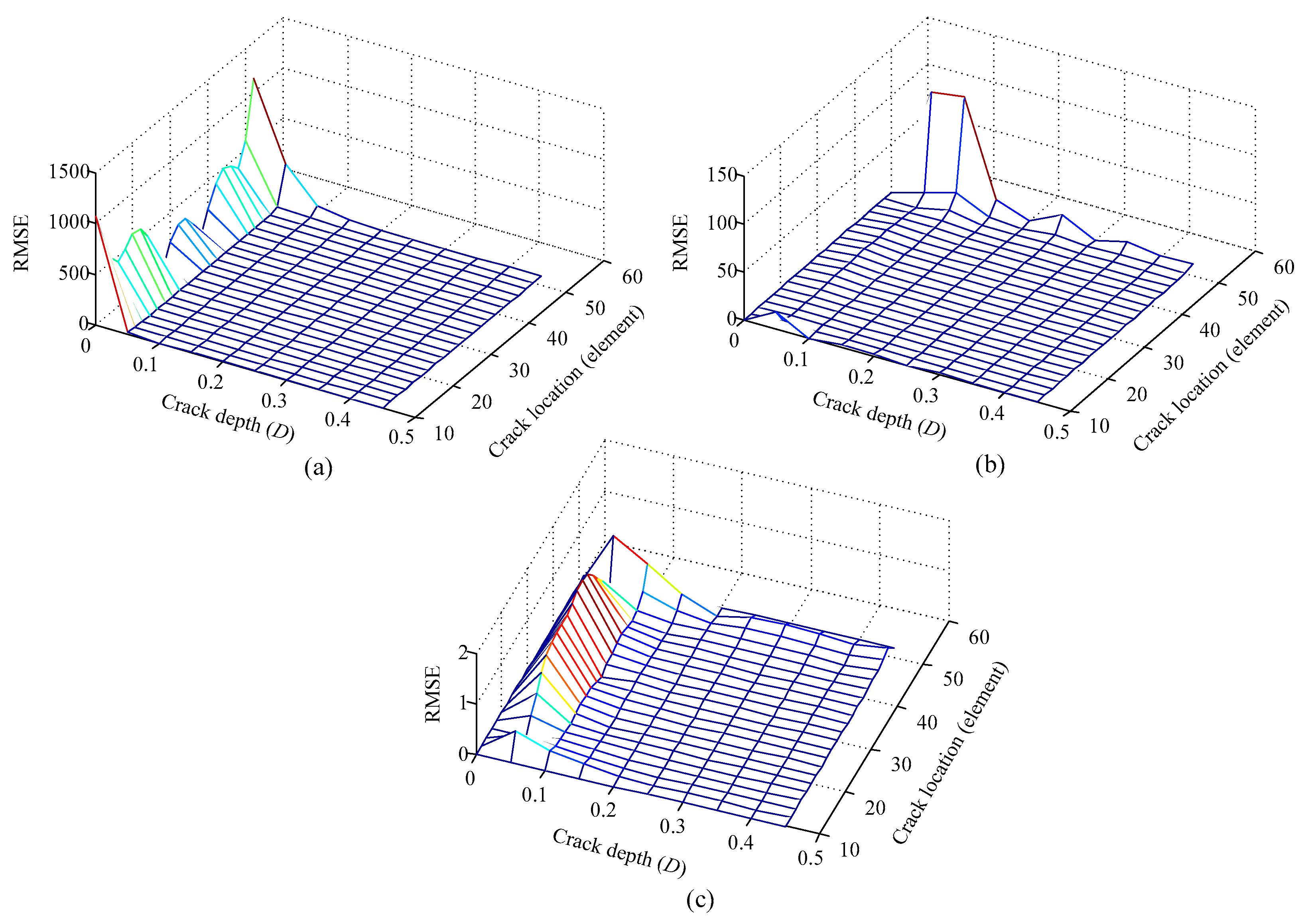
6.1. Prediction Error in the Entire Design Space
6.2. Results of Crack Identification
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bovsunovsky, A.; Surace, C. Non-linearities in the vibrations of elastic structures with a closing crack: A state of the art review. Mech. Syst. Signal Process. 2015, 62, 129–148. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Kumar, C.; Rastogi, V. A Brief Review on Dynamics of a Cracked Rotor. Int. J. Rotat. Mach. 2009, 2009, 1–6. [Google Scholar] [CrossRef]
- Papadopoulos, C.A. The strain energy release approach for modeling cracks in rotors: A state of the art review. Mech. Syst. Signal Process. 2008, 22, 763–789. [Google Scholar] [CrossRef]
- Yan, Y.J.; Cheng, L.; Wu, Z.Y.; Yam, L.H. Development in vibration-based structural damage detection technique. Mech. Syst. Signal Process. 2007, 21, 2198–2211. [Google Scholar] [CrossRef]
- Carden, E.P.; Fanning, P. Vibration Based Condition Monitoring: A Review. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Sabnavis, G.; Kirk, R.G.; Kasarda, M.; Quinn, D. Cracked shaft detection and diagnostics: A literature review. Shock Vib. Dig. 2004, 36, 287. [Google Scholar] [CrossRef]
- Sekhar, A.S. Model-based identification of two cracks in a rotor system. Mech. Syst. Signal Process. 2004, 18, 977–983. [Google Scholar] [CrossRef]
- Pennacchi, P.; Bachschmid, N.; Vania, A. A model-based identification method of transverse cracks in rotating shafts suitable for industrial machines. Mech. Syst. Signal Process. 2006, 20, 2112–2147. [Google Scholar] [CrossRef] [Green Version]
- Söffker, D.; Wei, C.; Wolff, S.; Saadawia, M.S. Detection of rotor cracks: Comparison of an old model-based approach with a new signal-based approach. Nonlinear Dyn. 2016, 83, 1153–1170. [Google Scholar] [CrossRef]
- Singh, S.; Tiwari, R. Model-Based Switching-Crack Identification in a Jeffcott Rotor With an Offset Disk Integrated With an Active Magnetic Bearing. J. Dyn. Syst. Meas. Control 2016, 138, 31006. [Google Scholar] [CrossRef]
- Saridakis, K.M.; Chasalevris, A.C.; Papadopoulos, C.A.; Dentsoras, A.J. Applying neural networks, genetic algorithms and fuzzy logic for the identification of cracks in shafts by using coupled response measurements. Comput. Struct. 2008, 86, 1318–1338. [Google Scholar] [CrossRef]
- Xiang, J.; Zhong, Y.; Chen, X.; He, Z. Crack detection in a shaft by combination of wavelet-based elements and genetic algorithm. Int. J. Solids Struct. 2008, 45, 4782–4795. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Yang, J.; Wang, Y.; Waisman, H.; Zhang, W. Probabilistic Model Updating for Sizing of Hole-Edge Crack Using Fiber Bragg Grating Sensors and the High-Order Extended Finite Element Method. Sensors 2016, 16, 1956. [Google Scholar] [CrossRef] [PubMed]
- Waisman, H.; Chatzi, E.; Smyth, A.W. Detection and quantification of flaws in structures by the extended finite element method and genetic algorithms. Int. J. Numer. Methods Eng. 2010, 82, 303–328. [Google Scholar] [CrossRef]
- Cavalini, A.A., Jr.; Sanches, L.; Bachschmid, N.; Steffen, V., Jr. Crack identification for rotating machines based on a nonlinear approach. Mech. Syst. Signal Process. 2016, 79, 72–85. [Google Scholar] [CrossRef]
- Vashisht, R.K.; Peng, Q. Crack detection in the rotor ball bearing system using switching control strategy and Short Time Fourier Transform. J. Sound Vib. 2018, 432, 502–529. [Google Scholar] [CrossRef]
- Qi, B.; Kong, Q.; Qian, H.; Patil, D.; Lim, I.; Li, M.; Liu, D.; Song, G. Study of Impact Damage in PVA-ECC Beam under Low-Velocity Impact Loading Using Piezoceramic Transducers and PVDF Thin-Film Transducers. Sensors 2018, 18, 671. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Chen, G.; Chen, B.; Li, Z.; Pan, J.; Zi, Y.; Yuan, J.; He, Z. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2016, 70–71, 1–35. [Google Scholar] [CrossRef]
- Hou, Q.; Ren, L.; Jiao, W.; Zou, P.; Song, G. An Improved Negative Pressure Wave Method for Natural Gas Pipeline Leak Location Using FBG Based Strain Sensor and Wavelet Transform. Math. Probl. Eng. 2013, 2013, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Luo, M.; Li, T.; Song, G. ECG Signal De-noising and Baseline Wander Correction Based on CEEMDAN and Wavelet Threshold. Sensors 2017, 17, 2754. [Google Scholar] [CrossRef] [PubMed]
- Elbouchikhi, E.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H.; Turri, S. An Efficient Hilbert-Huang Transform-based Bearing Faults Detection in Induction Machines. IEEE Trans. Energy Convers. 2017, 32, 401–413. [Google Scholar] [CrossRef]
- Chen, B.; Hei, C.; Luo, M.; Ho, M.S.; Song, G. Pipeline two-dimensional impact location determination using time of arrival with instant phase (TOAIP) with piezoceramic transducer array. Smart Mater. Struct. 2018, 27, 105003. [Google Scholar] [CrossRef]
- Chandra, N.H.; Sekhar, A.S. Fault detection in rotor bearing systems using time frequency techniques. Mech. Syst. Signal Process. 2016, 72, 105–133. [Google Scholar] [CrossRef]
- Sampaio, D.L.; Nicoletti, R. Detection of cracks in shafts with the Approximated Entropy algorithm. Mech. Syst. Signal Process. 2016, 72, 286–302. [Google Scholar] [CrossRef]
- Shravankumar, C.; Tiwari, R. Detection of a fatigue crack in a rotor system using full-spectrum based estimation. Sadhana 2016, 41, 239–251. [Google Scholar] [CrossRef]
- Yang, L.; Chen, X.; Wang, S. A novel amplitude-independent crack identification method for rotating shaft. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4098–4112. [Google Scholar] [CrossRef]
- Xie, J.; Cheng, W.; Zi, Y.; Zhang, M. Phase-based spectrum analysis method for identifying weak harmonics. J. Vib. Control 2018, 24, 5585–5596. [Google Scholar] [CrossRef]
- Dong, H.B.; Chen, X.F.; Li, B.; Qi, K.Y.; He, Z.J. Rotor crack detection based on high-precision modal parameter identification method and wavelet finite element model. Mech. Syst. Signal Process. 2009, 23, 869–883. [Google Scholar] [CrossRef]
- Liu, F.; Gao, S.; Han, H.; Tian, Z.; Liu, P. Interference reduction of high-energy noise for modal parameter identification of offshore wind turbines based on iterative signal extraction. Ocean Eng. 2019. [Google Scholar] [CrossRef]
- Rubio, L.; Fernández-Sáez, J.; Morassi, A. Identification of two cracks in a rod by minimal resonant and antiresonant frequency data. Mech. Syst. Signal Process. 2015, 60, 1–13. [Google Scholar] [CrossRef]
- Rahman, A.G.A.; Ismail, Z.; Noroozi, S.; Chao, O.Z. Study of open crack in rotor shaft using changes in frequency response function phase. Int. J. Damage Mech. 2013, 22, 791–807. [Google Scholar] [CrossRef]
- Seo, Y.; Lee, C.; Park, K.C. Crack Identification in a Rotating Shaft via the Reverse Directional Frequency Response Functions. J. Vib. Acoust. 2009, 131, 11012. [Google Scholar] [CrossRef]
- Hou, Q.; Jiao, W.; Ren, L.; Cao, H.; Song, G. Experimental study of leakage detection of natural gas pipeline using FBG based strain sensor and least square support vector machine. J. Loss Prev. Process Ind. 2014, 32, 144–151. [Google Scholar] [CrossRef]
- Zapico-Valle, J.L.; Rodríguez, E.; García-Diéguez, M.; Cortizo, J.L. Rotor crack identification based on neural networks and modal data. Meccanica 2014, 49, 305–324. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The sensitivity method in finite element model updating: A tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Alkayem, N.F.; Cao, M.; Zhang, Y.; Bayat, M.; Su, Z. Structural damage detection using finite element model updating with evolutionary algorithms: A survey. Neural Comput. Appl. 2018, 30, 389. [Google Scholar] [CrossRef]
- Shabbir, F.; Khan, M.; Ahmad, N.; Tahir, M.; Ejaz, N.; Hussain, J. Structural Damage Detection with Different Objective Functions in Noisy Conditions Using an Evolutionary Algorithm. Appl. Sci. 2017, 7, 1245. [Google Scholar] [CrossRef]
- Rocchetta, R.; Broggi, M.; Huchet, Q.; Patelli, E. On-line Bayesian model updating for structural health monitoring. Mech. Syst. Signal Process. 2018, 103, 174–195. [Google Scholar] [CrossRef]
- Bi, S.; Broggi, M.; Beer, M. The role of the Bhattacharyya distance in stochastic model updating. Mech. Syst. Signal Process. 2019, 117, 437–452. [Google Scholar] [CrossRef]
- Patel, T.H.; Zuo, M.J.; Darpe, A.K. Vibration response of coupled rotor systems with crack and misalignment. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 700–713. [Google Scholar] [CrossRef]
- Reddy, M.C.S.; Sekhar, A.S. Detection and monitoring of coupling misalignment in rotors using torque measurements. Measurement 2015, 61, 111–122. [Google Scholar] [CrossRef]
- Jiang, T.; Kong, Q.; Patil, D.; Luo, Z.; Huo, L.; Song, G. Detection of Debonding Between Fiber Reinforced Polymer Bar and Concrete Structure Using Piezoceramic Transducers and Wavelet Packet Analysis. IEEE Sens. J. 2017, 17, 1992–1998. [Google Scholar] [CrossRef]
- Li, D.; Liang, Y.; Feng, Q.; Song, G. Load monitoring of the pin-connected structure based on wavelet packet analysis using piezoceramic transducers. Measurement 2018, 122, 638–647. [Google Scholar] [CrossRef]
- Xiang, J.; Zhong, Y. A Novel Personalized Diagnosis Methodology Using Numerical Simulation and an Intelligent Method to Detect Faults in a Shaft. Appl. Sci. 2016, 6, 414. [Google Scholar] [CrossRef]
- Gómez, M.J.; Castejón, C.; García-Prada, J.C. Crack detection in rotating shafts based on 3× energy: Analytical and experimental analyses. Mech. Mach. Theory 2016, 96, 94–106. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Song, G. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Wang, T.; Li, H.; Song, G. Health degradation monitoring and early fault diagnosis of a rolling bearing based on CEEMDAN and improved MMSE. Materials 2018, 11, 1009. [Google Scholar] [CrossRef]
- Yuan, R.; Lv, Y.; Song, G. Multi-Fault Diagnosis of Rolling Bearings via Adaptive Projection Intrinsically Transformed Multivariate Empirical Mode Decomposition and High Order Singular Value Decomposition. Sensors 2018, 18, 1210. [Google Scholar] [CrossRef]
- Guo, C.; Yan, J.; Yang, W. Crack detection for a Jeffcott rotor with a transverse crack: An experimental investigation. Mech. Syst. Signal Process. 2017, 83, 260–271. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Nobari, A.; Ouyang, H.; Bannister, P. Uncertainty quantification of squeal instability via surrogate modelling. Mech. Syst. Signal Process. 2015, 60, 887–908. [Google Scholar] [CrossRef]
- Han, F.; Guo, X.; Gao, H. Bearing parameter identification of rotor-bearing system based on Kriging surrogate model and evolutionary algorithm. J. Sound Vib. 2013, 332, 2659–2671. [Google Scholar] [CrossRef]
- Gao, H.; Guo, X.; Ouyang, H.; Han, F. Crack Identification of Cantilever Plates Based on a Kriging Surrogate Model. J. Vib. Acoust. 2013, 135, 51012. [Google Scholar] [CrossRef] [PubMed]
- Darpe, A.K.; Gupta, K.; Chawla, A. Coupled bending, longitudinal and torsional vibrations of a cracked rotor. J. Sound Vib. 2004, 269, 33–60. [Google Scholar] [CrossRef]
- Lu, Z.; Dong, D.; Ouyang, H.; Cao, S.; Hua, C. Localization of breathing cracks in stepped rotors using super-harmonic characteristic deflection shapes based on singular value decomposition in frequency domain. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1825–1837. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar]
- Sinou, J.; Lees, A.W. The influence of cracks in rotating shafts. J. Sound Vib. 2005, 285, 1015–1037. [Google Scholar] [CrossRef] [Green Version]
- Forrester, A.; Sobester, A.; Keane, A. Engineering Design Via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zhang, X.; Gao, R.X.; Yan, R.; Chen, X.; Sun, C.; Yang, Z. Multivariable wavelet finite element-based vibration model for quantitative crack identification by using particle swarm optimization. J. Sound Vib. 2016, 375, 200–216. [Google Scholar] [CrossRef]
- Mao, Y.M.; Guo, X.L.; Zhao, Y. A state space force identification method based on Markov parameters precise computation and regularization technique. J. Sound Vib. 2010, 329, 3008–3019. [Google Scholar] [CrossRef]









| Feature | Value (Units) | Feature | Value (Units) |
|---|---|---|---|
| Shaft length (l0) | 0.6 m | Mass of disc 1 | 0.759 kg |
| l1 | 0.46 m | polar moment of inertia of disc 1 | 5.758 × 10−4 kg·m2 |
| l2 | 0.07 m | diametrical moment of inertia of disc 1 | 3.177 × 10−4 kg·m2 |
| l3 | 0.08 m | Mass of disc 2 | 0.770 kg |
| l4 | 0.1 m | polar moment of inertia of disc 2 | 5.843 × 10−4 kg·m2 |
| Shaft diameter (D) | 0.01 m | diametrical moment of inertia of disc 2 | 3.232 × 10−4 kg·m2 |
| density (40Cr) | 7.87 × 103 kg·m−3 | Gravitational acceleration | 9.8 m/s2 |
| Yang’s modulus | 2.11 × 1011 Pa | Rayleigh damping coefficient (a) | 0.68 |
| Poisson’s ratio | 0.277 | Rayleigh damping coefficient (b) | 2.8 × 10−5 |
| Order | Beam Model | ABAQUS | Measured | Error between Beam Model and ABAQUS | Error between Beam Model and Measured Results |
|---|---|---|---|---|---|
| 1st vertical bending | 42.1 Hz | 40.9 Hz | 42.5 Hz | 1.2 Hz (2.85%) | 0.4 Hz (0.95%) |
| 1st lateral bending | 42.1 Hz | 41.0 Hz | 42.9 Hz | 1.1 Hz (2.61%) | 0.8 Hz (1.90%) |
| 2nd vertical bending | 107.9 Hz | 112.4 Hz | 107.4 Hz | 4.5 Hz (4.17%) | 0.5 Hz (0.47%) |
| 2nd lateral bending | 107.9 Hz | 112.4 Hz | 108.7 Hz | 4.5 Hz (4.17%) | 0.8 Hz (0.74%) |
| 1st torsion | 158.8 Hz | 160.2 Hz | - | 1.4 Hz (0.88%) | - |
| 3rd vertical bending | 349.6 Hz | 358.0 Hz | 349.6 Hz | 8.4 Hz (2.40%) | 0.0 Hz (0.00%) |
| 3rd lateral bending | 349.6 Hz | 357.2 Hz | 350.7 Hz | 7.6 Hz (2.17%) | 1.1 Hz (0.31%) |
| Under-Test Sample Number | Actual Parameters | Identified Results | Updating Times | Criterion Values for the Final Updated Model | ||
|---|---|---|---|---|---|---|
| Crack Location (Element) | Crack Depth (D) | Crack Location (Element) | Crack Depth (D) | |||
| 1 | 34 | 0.1 | 32 | 0.1 | 1 | (1, 0.96) |
| 2 | 46 | 0.05 | 46 | 0.05 | 4 | (1, 1) |
| 3 | 50 | 0.35 | 50 | 0.35 | 5 | (1, 1) |
| 4 | 28 | 0.25 | 28 | 0.25 | 2 | (1, 1) |
| 5 | 20 | 0.4 | 20 | 0.4 | 2 | (0.99, 0.99) |
| 6 | 12 | 0.3 | 12 | 0.3 | 5 | (1, 1) |
| 7 | 42 | 0.2 | 42 | 0.2 | 3 | (1, 1) |
| 8 | 38 | 0.45 | 38 | 0.45 | 2 | (1, 1) |
| 9 | 16 | 0.15 | 16 | 0.15 | 3 | (1, 1) |
| 10 | 24 | 0 | 28 | 0 | 1 | (1, 1) |
| Under-Test Sample Number | Actual Parameters | Identified Results | Updating Times | Criterion Values for the Final Updated Model | ||
|---|---|---|---|---|---|---|
| Crack Location (Element) | Crack Depth (D) | Crack Location (Element) | Crack Depth (D) | |||
| 1 | 34 | 0.1 | 34 | 0.1 | 2 | (1, 1) |
| 2 | 46 | 0.05 | 50 | 0.1 | 8 | (1, 0.95) |
| 3 | 50 | 0.35 | 50 | 0.35 | 9 | (1, 1) |
| 4 | 28 | 0.25 | 28 | 0.25 | 1 | (0.99, 0.99) |
| 5 | 20 | 0.4 | 20 | 0.4 | 2 | (1, 1) |
| 6 | 12 | 0.3 | 12 | 0.3 | 10 | (1, 1) |
| 7 | 42 | 0.2 | 42 | 0.2 | 4 | (1, 1) |
| 8 | 38 | 0.45 | 36 | 0.45 | 1 | (1, 0.96) |
| 9 | 16 | 0.15 | 16 | 0.15 | 2 | (1, 1) |
| 10 | 24 | 0 | 24 | 0 | 1 | (1, 1) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Lv, Y.; Ouyang, H. A Super-Harmonic Feature Based Updating Method for Crack Identification in Rotors Using a Kriging Surrogate Model. Appl. Sci. 2019, 9, 2428. https://doi.org/10.3390/app9122428
Lu Z, Lv Y, Ouyang H. A Super-Harmonic Feature Based Updating Method for Crack Identification in Rotors Using a Kriging Surrogate Model. Applied Sciences. 2019; 9(12):2428. https://doi.org/10.3390/app9122428
Chicago/Turabian StyleLu, Zhiwen, Yong Lv, and Huajiang Ouyang. 2019. "A Super-Harmonic Feature Based Updating Method for Crack Identification in Rotors Using a Kriging Surrogate Model" Applied Sciences 9, no. 12: 2428. https://doi.org/10.3390/app9122428
APA StyleLu, Z., Lv, Y., & Ouyang, H. (2019). A Super-Harmonic Feature Based Updating Method for Crack Identification in Rotors Using a Kriging Surrogate Model. Applied Sciences, 9(12), 2428. https://doi.org/10.3390/app9122428







