Numerical Study on Gaseous CO2 Leakage and Thermal Characteristics of Containers in a Transport Ship
Abstract
:1. Introduction
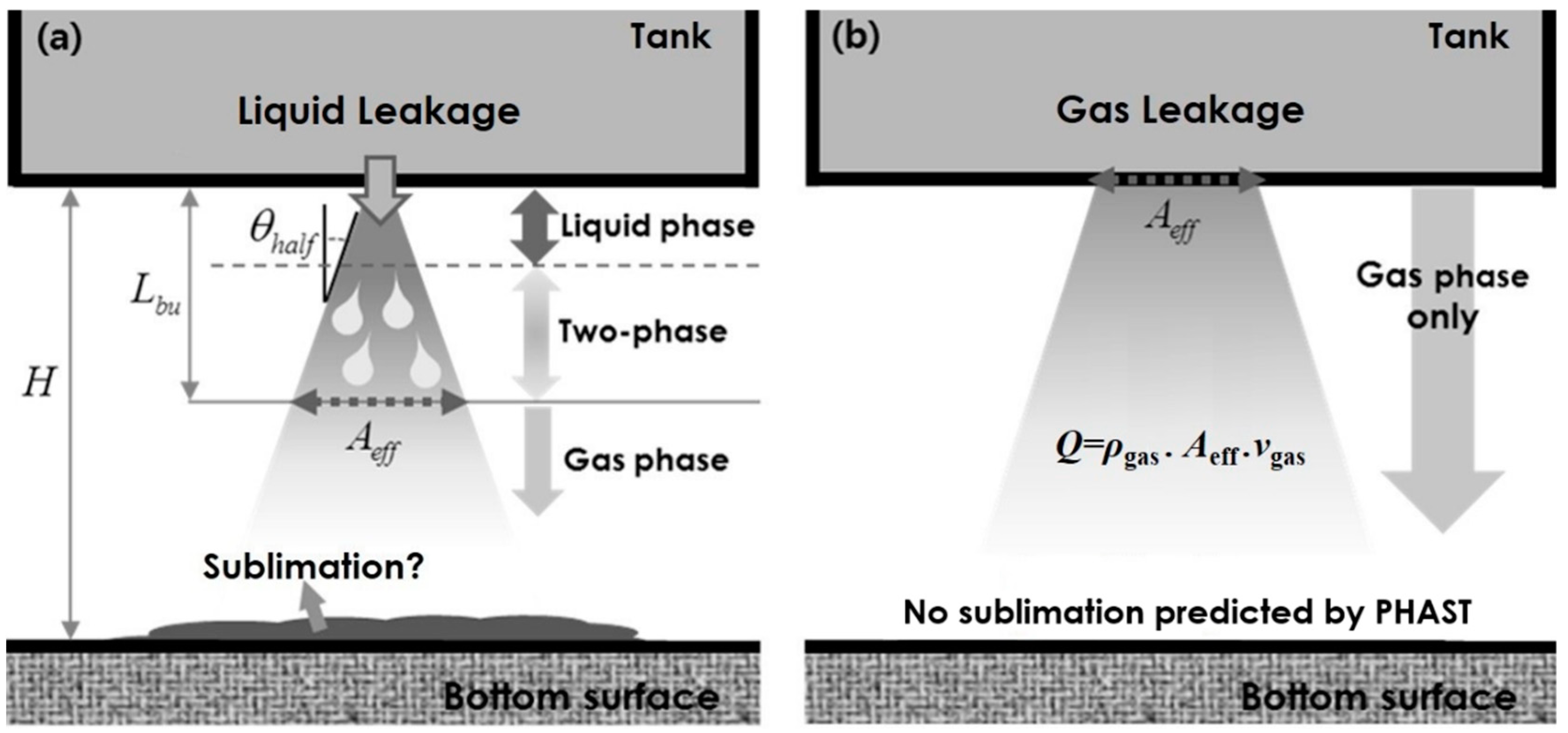
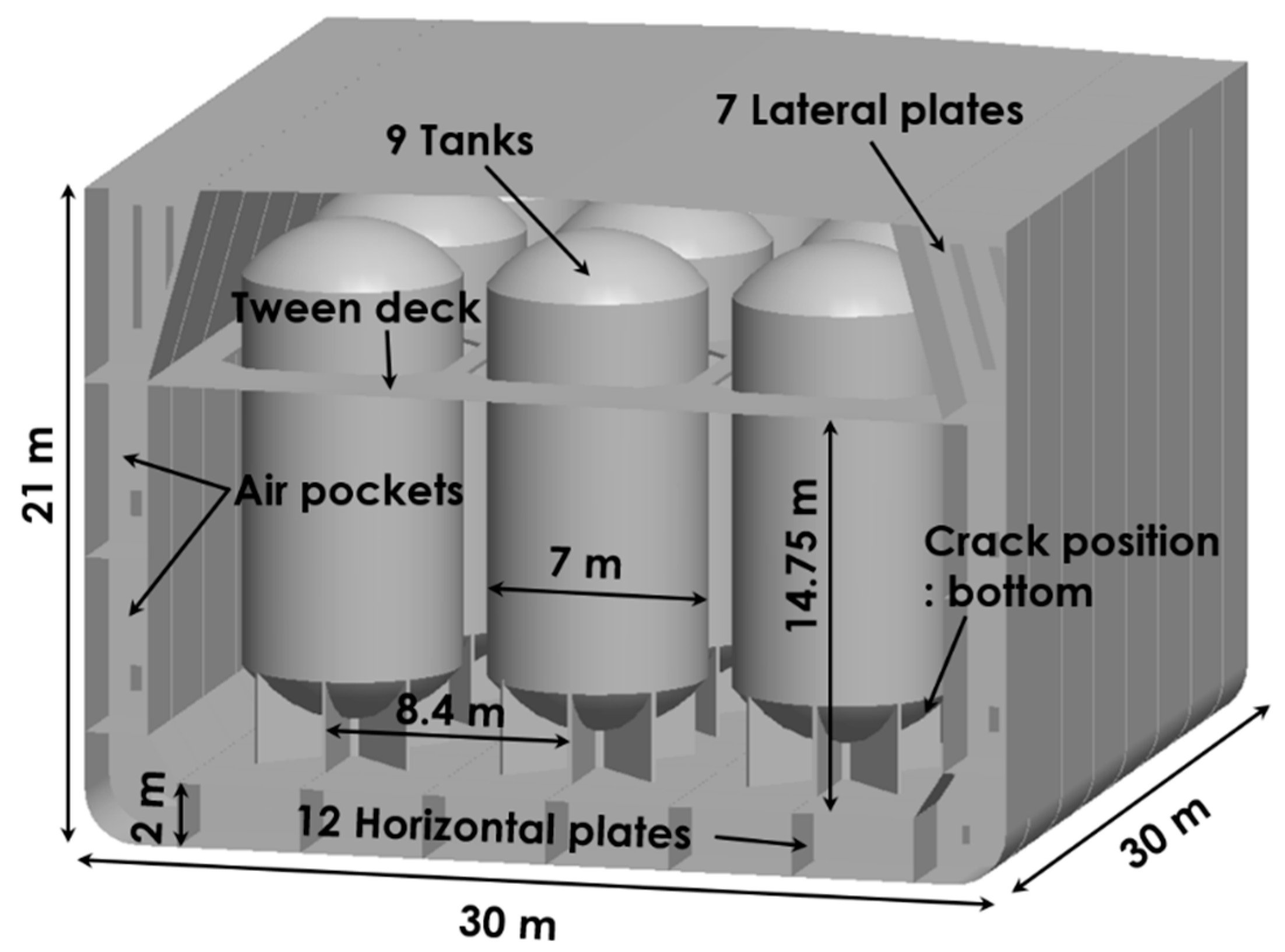
2. Modeling of Gas Leakage
3. Mathematical Representations for CFD Simulations
4. Results and Discussion
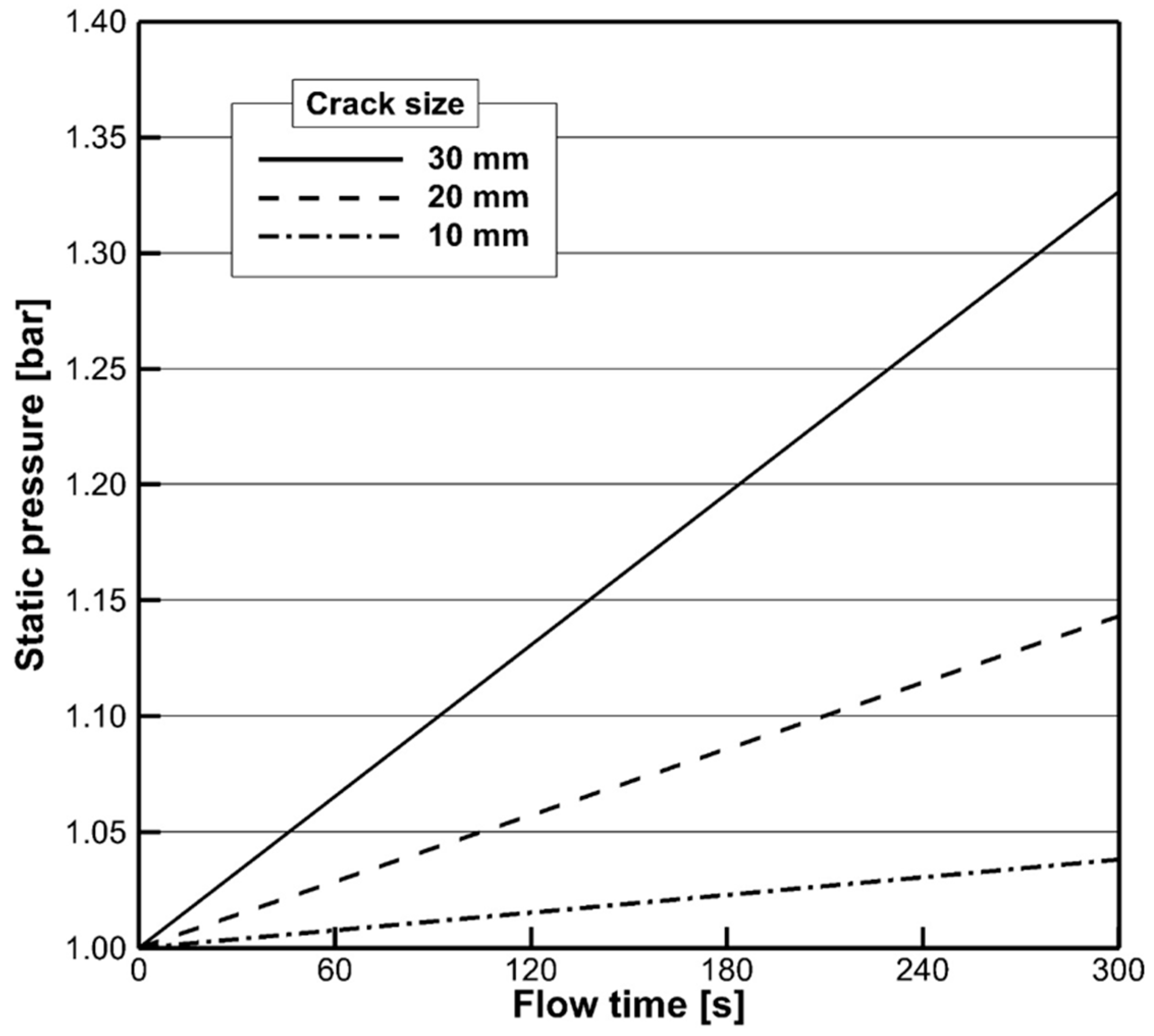
4.1. Flow Characteristics
4.2. Accumulation of CO2 Concentration
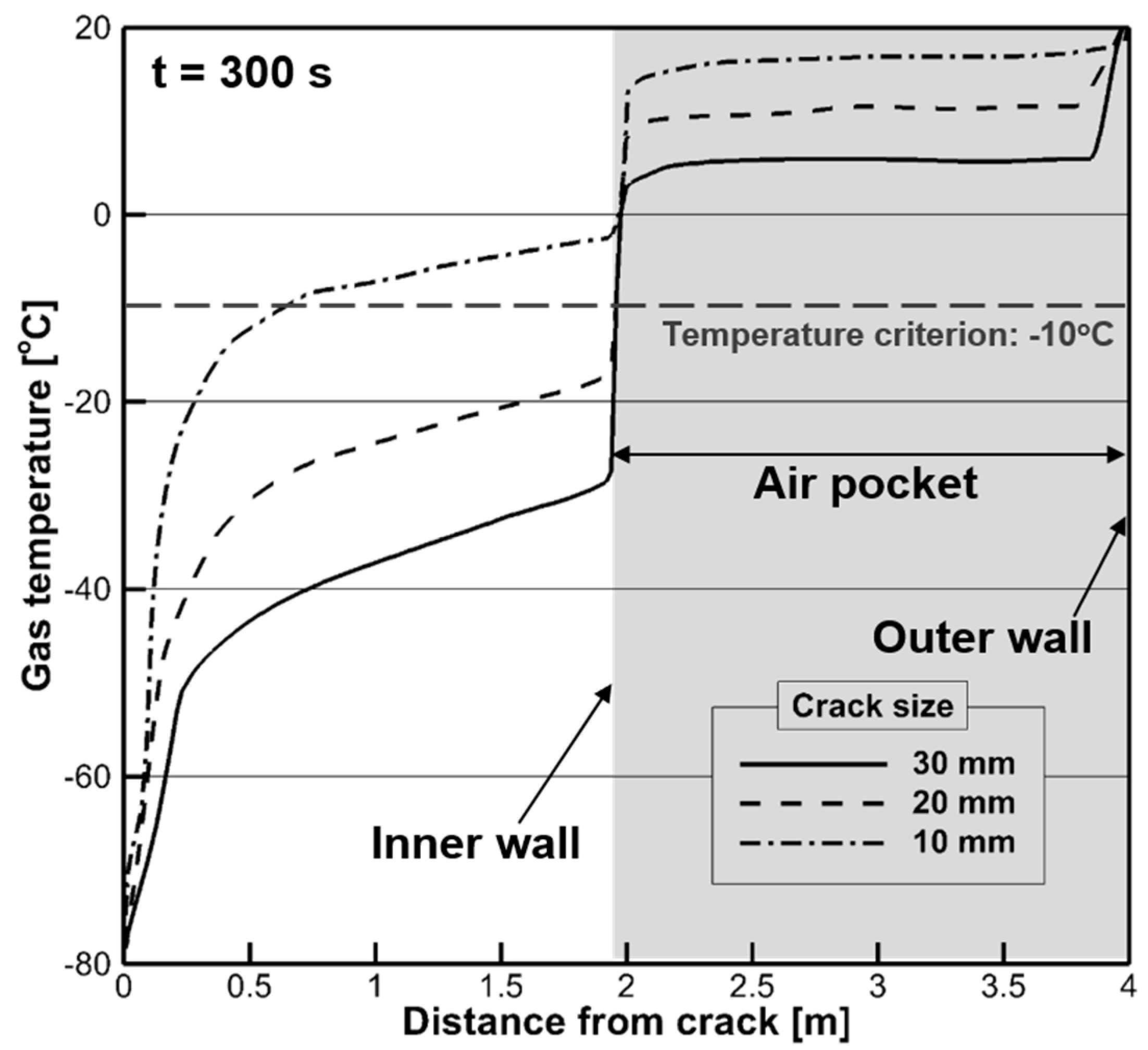
4.3. Evolution of Wall Temperature
5. Conclusions
- Considering the phase change, the gas velocity exhausted from the crack was estimated by considering rapid gas expansion. According to the mass conservation principle, an effective crack area was calculated for making appropriate boundary conditions for CFD simulations. The ejected gas flow was rapidly diffused and impinged on solid surfaces. In particular, the CO2 concentration changed rapidly depending on the crack size. The present study provided the evolution of a dangerous volume with a CO2 concentration above 10 %, showing an increasing tendency as the crack size increased.
- Numerical results showed that the leaked CO2 gas rarely propagated toward the upper tween deck region because of the buoyancy effect. For a crack size of 30 mm, it was predicted that the entire region below the tween deck could become a dangerous volume within 300 s. Moreover, a substantial difference in dangerous volume with differing crack sizes was observed at the initial stage of leakage. The present CFD result supported the fact that, for quick detection before propagation, the gas sensors should be mounted near the bottom corners of the container of a transport ship.
- The temperature profile from the crack to the air pocket exhibited a decreasing tendency as the crack size increased. The solid temperature of the impingement surface decreased rapidly below the design temperature when the crack size was larger than 20 mm. However, the sudden change in the wall temperature was delayed owing to the conjugate heat transfer from the air pocket.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Metz, B.; Davidson, O.; de Coninck, H.; Loos, M.; Meyer, L. IPCC Special Report on Carbon Dioxide Capture, Storage; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- McCoy, S.T.; Rubin, E.S. An engineering-economic model of pipeline transport of CO2 with application to carbon capture and storage. Int. J. Greenh. Gas Control 2008, 2, 219–229. [Google Scholar] [CrossRef]
- Michael, K.; Golab, A.; Shulakova, V.; Ennis-Kng, J.; Allinson, G.; Sharma, S.; Aiken, T. Geological storage of CO2 in saline aquifers-A review of the experience from existing storage operations. Int. J. Greenh. Gas Control 2010, 4, 659–667. [Google Scholar] [CrossRef]
- Pires, J.C.M.; Martins, F.G.; Aluim-Ferraz, M.C.M.; Simoes, M. Recent development on carbon capture and storage: An overview. Chem. Eng. Res. Des. 2011, 89, 1446–1460. [Google Scholar] [CrossRef]
- Svensson, R.; Odenberger, M.; Johnsson, F.; Stromberg, L. Transportation systems for CO2-application to carbon capture and storage. Energy Convers. Manag. 2004, 45, 2343–2353. [Google Scholar] [CrossRef]
- Jeon, S.H.; Choi, Y.U.; Kim, M.S. Review on boil-off gas (BOG) re-liquefaction system of liquefied CO2 transport ship for carbon capture and sequestration (CCS). Int. J. Air-Cond. Refrig. 2016, 24, 1650017. [Google Scholar] [CrossRef]
- Yoo, B.Y.; Choi, D.-K.; Huh, C.; Kang, S.-G.; Kim, I.-S. A feasibility study on CO2 marine transport in South Korea. Energy Procedia 2013, 37, 3199–3211. [Google Scholar] [CrossRef]
- Vandeginste, V.; Piessens, K. Pipeline design for a least-cost router application for CO2 transport in the CO2 sequestration cycle. Int. J. Greenh. Gas Control 2008, 2, 571–581. [Google Scholar] [CrossRef]
- Jeon, S.H.; Kim, M.S. Compressor selection methods for multi-stage re-liquefaction system of liquefies CO2 transport ship for CCS. Appl. Therm. Eng. 2015, 82, 360–367. [Google Scholar] [CrossRef]
- Mazzoldi, A.; Hill, T.; Colls, J.J. CFD and Gaussian atmospheric dispersion models: A comparison for leak from carbon dioxide transportation and storage facilities. Atmos. Environ. 2008, 42, 8046–8054. [Google Scholar] [CrossRef]
- Wang, Z.; Fimbres Weihs, G.A.; Cardenas, G.I.; Wiley, D.E. Optimal pipeline design for CCS projects with anticipated increasing CO2 flow rates. Int. J. Greenh. Gas Control 2014, 31, 165–174. [Google Scholar] [CrossRef]
- Mazzoldi, A.; Hill, T.; Colls, J.J. CO2 transportation for carbon capture and storage: Sublimation of carbon dioxide from a dry ice bank. Int. J. Greenh. Gas Control 2008, 2, 210–218. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Wang, G.X.; Massarotto, P.; Rudolph, V. Optimization of pipeline transport for CO2 sequestration. Energy Convers. Manag. 2006, 47, 702–715. [Google Scholar] [CrossRef]
- Okumoto, Y.; Takeda, Y.; Mano, M.; Okada, T. Design of Ship Hull Structures—A Practical Guide for Engineers; Springer: New York, NY, USA, 2009. [Google Scholar]
- Minescu, M.; Pana, I. Safety evaluation of the pipelines systems for petroleum products. Appl. Mech. Mater. 2013, 371, 782–786. [Google Scholar] [CrossRef]
- Eparu, C.; Albulescu, M.; Neacsu, S.; Albulescu, C. Gas leaks through corrosion defects of buried gas transmission pipelines. Rev. Chim-Buchar. 2014, 65, 1385–1390. [Google Scholar]
- Bai, M. Risk assessment for CO2 leakage along abandoned wells using a Monte Carlo simulation in a CO2 sequestration site. Pet. Sci. Technol. 2014, 32, 1191–1200. [Google Scholar] [CrossRef]
- Calay, R.K.; Holdo, A.E. Modelling the dispersion of flashing jets using CFD. J. Hazard. Mater. 2008, 154, 1198–1209. [Google Scholar] [CrossRef] [PubMed]
- Laryea, G.N.; No, S.Y. Spray angle and breakup length of charge-injected electrostatic pressure-swirl nozzle. J. Electrost. 2004, 60, 37–47. [Google Scholar] [CrossRef]
- Ghurri, A.; Kim, J.D.; Kim, H.G.; Jung, J.Y.; Song, K.K. The effect of injection pressure and fuel viscosity on the spray characteristics of biodiesel blends injected into an atmospheric chamber. J. Mech. Sci. Technol. 2012, 26, 2941–2947. [Google Scholar] [CrossRef]
- DNV Software. Droplet Size Theory Document; Palace House: London, UK, 2011. [Google Scholar]
- Holterman, H.J. Kinetics and Evaporation of Water Drops in Air; IMAG Report; Institute of Agricultural and Environmental Engendering: Wageningen, The Netherlands, 2012. [Google Scholar]
- ANSYS Inc. Ansys Fluent User’s Guide 16.1; ANSYS Inc.: Canonsburg, PA, USA, 2010. [Google Scholar]
- Kim, K.; Kang, H.; Kim, Y. Risk assessment for natural gas hydrate carriers: A hazard identification (HAZID) study. Energies 2015, 8, 3142–3164. [Google Scholar] [CrossRef]
- Hong, S.K.; Cho, H.H. The review of studies on heat transfer in impinging jet. Int. J. Air-Cond. Refrig. 2005, 13, 196–205. [Google Scholar]
- Anderson, A.; Johns, F.R. Characteristics of free supersonic jets exhausting into quiescent air. J. Jet Propuls. 1955, 25, 13–15. [Google Scholar] [CrossRef]
- Langford, N.J. Carbon dioxide poisoning. Toxicol. Rev. 2005, 24, 229–235. [Google Scholar] [CrossRef] [PubMed]
- Canadian Center for Occupational and Health and Safety (CCOHS). Chemical Profiles—Carbon Dioxide; CCOHS: Hamilton, ON, Canada, 2005; Available online: http://www.ccohs.ca/oshanswers/ (accessed on 30 April 2018).
- IMO Publication. IGC Code: International Code for the Construction and Equipment of Ships Carrying Liquefied Gases in Bulk (IA 104E); IMO Publication: London, UK, 2016. [Google Scholar]






| Description (unit) | Detail | Note |
|---|---|---|
| Crack size (mm) | 10/20/30 | |
| Mass flow rate (kg/s) | 2.175/8.698/19.569 | estimation by PHAST |
| Effective crack size (mm) | 66/132/198 | |
| Density (kg/m3) | air@20°C = 1.225 CO2@20°C = 1.789 | ideal gas law |
| Heat capacity (J/kg∙K) | air@20°C = 1006.43 CO2@20°C = 847.07 | piecewise-polynomial profile |
| Thermal conductivity (W/m∙K) | air@20°C = 0.0242 CO2@20°C = 0.0145 steel@20°C = 16.27 | piecewise-polynomial profile |
| Inlet conditions | TCO2 = −78.37 °C YCO2 = 1 | saturation temperature of CO2 at 1 bar [9] |
| Initial environmental conditions | Tair = 20 °C Yair = 1 | room temperature |
| Boundary conditions | Tamb = 20 °C | ambient temperature |
| Design temperature | Tdesign = −10 °C | damage to AH steel [14] |
| CO2 concentration limit | YCO2 = 0.1 | injury to humans |
| Flow time (s) | 300 | sufficient time to analyze the gas propagation |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.Y.; Jeong, C.H.; Park, B.J.; Ki, M.S.; Shin, M.-S.; Lee, S.H. Numerical Study on Gaseous CO2 Leakage and Thermal Characteristics of Containers in a Transport Ship. Appl. Sci. 2019, 9, 2536. https://doi.org/10.3390/app9122536
Kim DY, Jeong CH, Park BJ, Ki MS, Shin M-S, Lee SH. Numerical Study on Gaseous CO2 Leakage and Thermal Characteristics of Containers in a Transport Ship. Applied Sciences. 2019; 9(12):2536. https://doi.org/10.3390/app9122536
Chicago/Turabian StyleKim, Dae Yun, Chan Ho Jeong, Beom Jin Park, Min Suk Ki, Myung-Soo Shin, and Seong Hyuk Lee. 2019. "Numerical Study on Gaseous CO2 Leakage and Thermal Characteristics of Containers in a Transport Ship" Applied Sciences 9, no. 12: 2536. https://doi.org/10.3390/app9122536
APA StyleKim, D. Y., Jeong, C. H., Park, B. J., Ki, M. S., Shin, M.-S., & Lee, S. H. (2019). Numerical Study on Gaseous CO2 Leakage and Thermal Characteristics of Containers in a Transport Ship. Applied Sciences, 9(12), 2536. https://doi.org/10.3390/app9122536





