Dynamic Modeling of McKibben Muscle Using Empirical Model and Particle Swarm Optimization Method
Abstract
:Featured Application
Abstract
1. Introduction
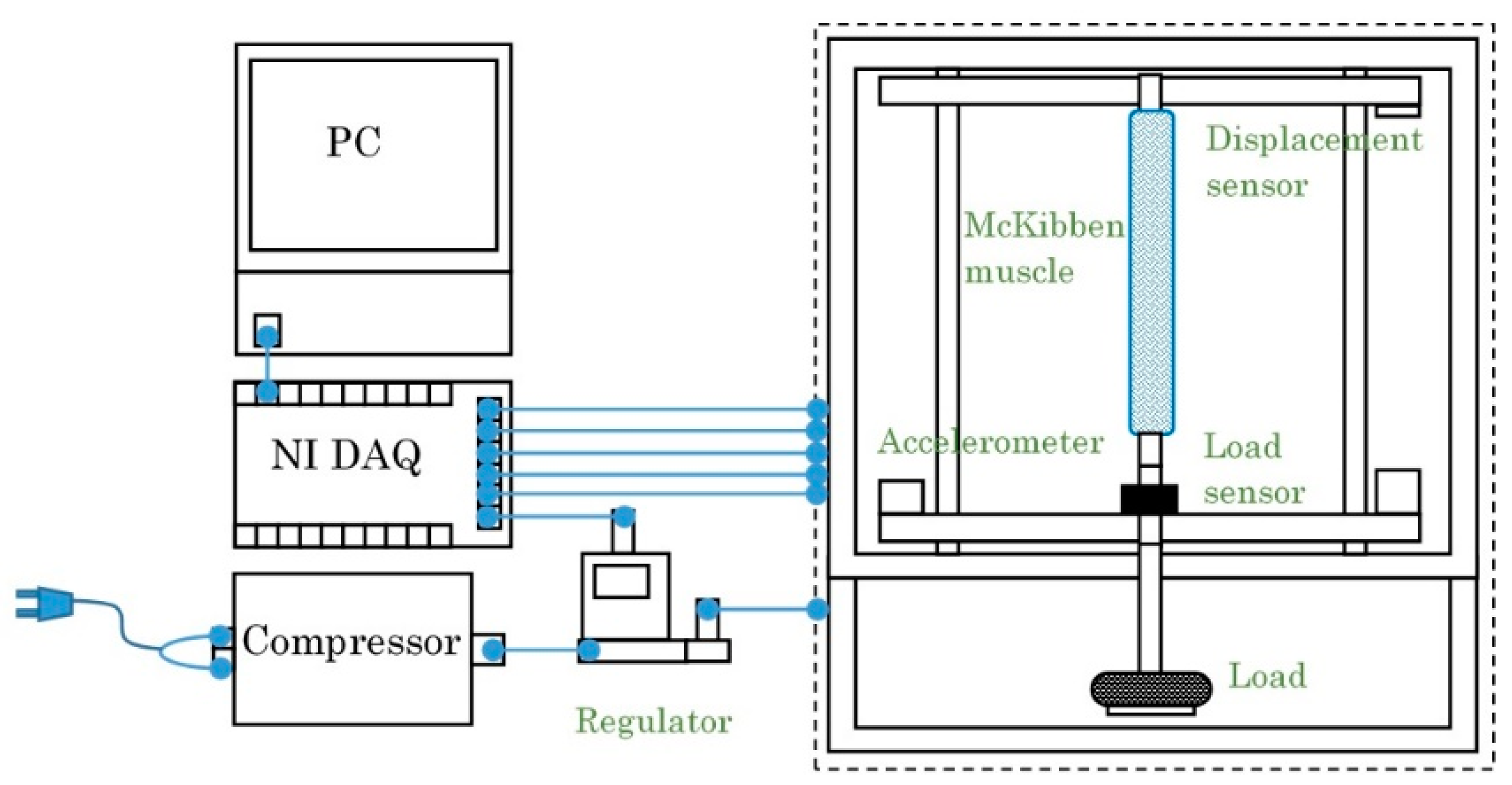
2. Materials and Methods
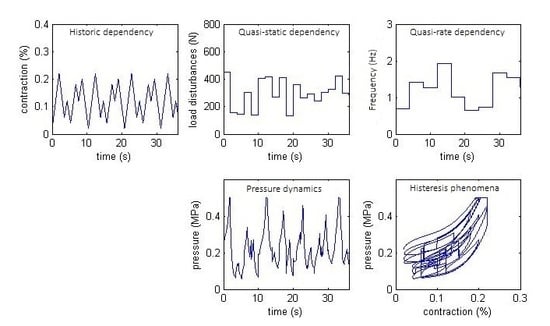
3. Hysteresis Phenomena
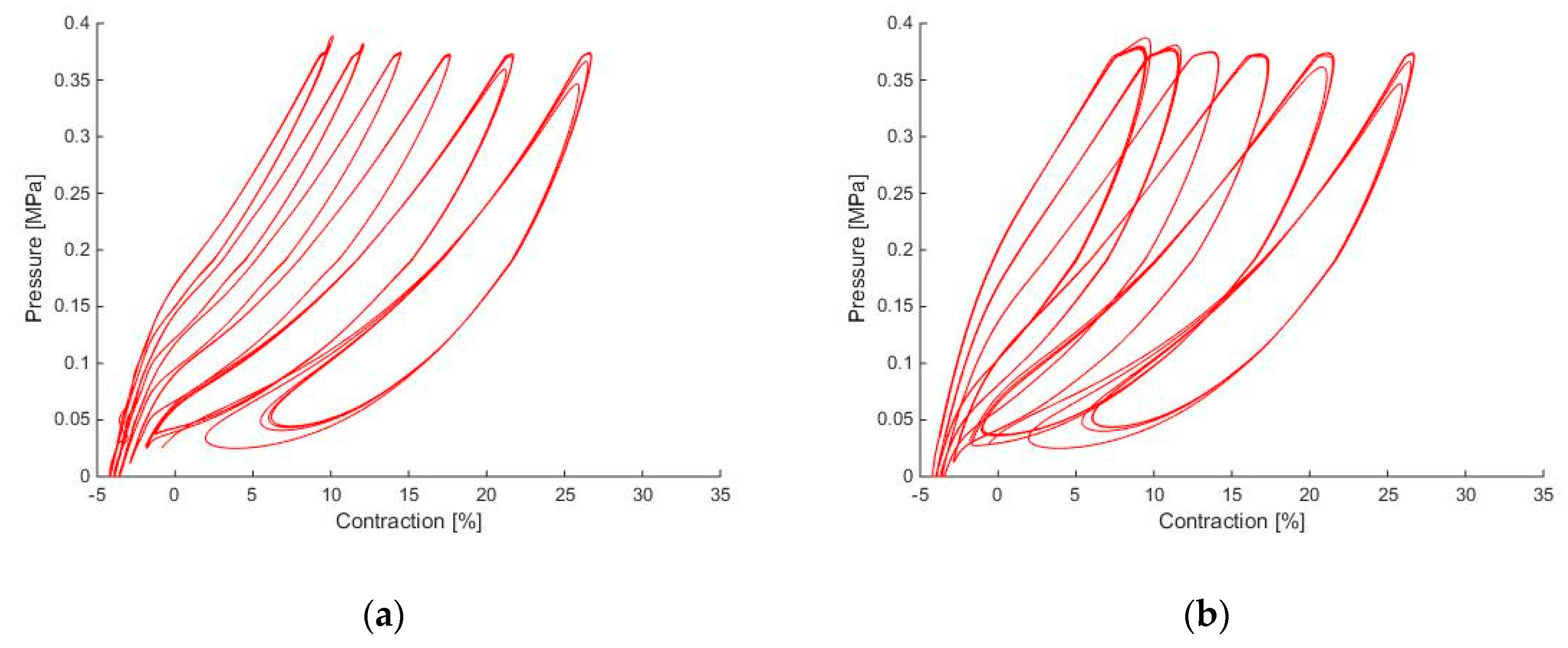
Hysteresis Data Characterization
4. Parametric Identification of the McKibben Muscle Model
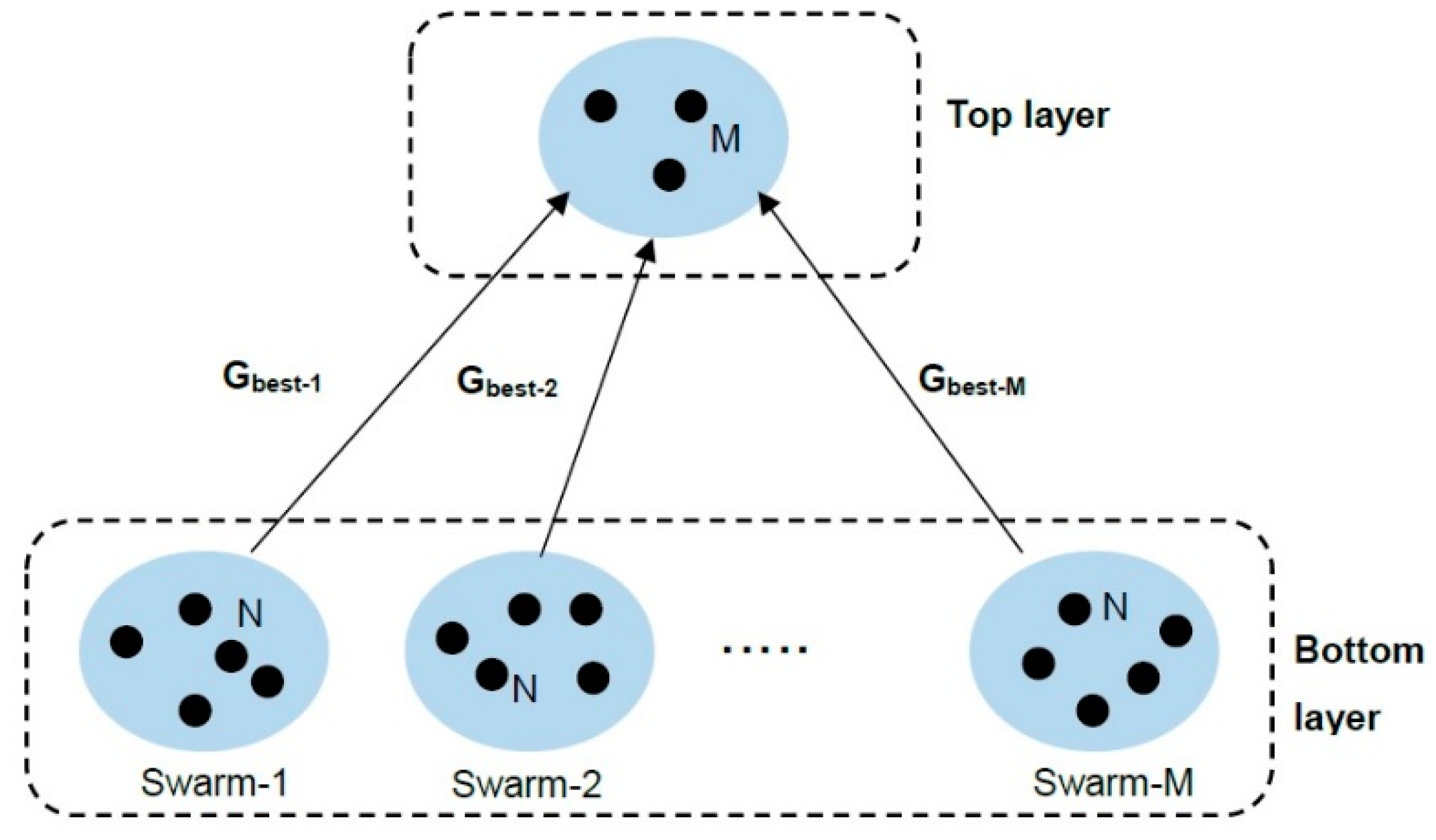
Particle Swarm Optimization
5. Empirical Modeling of the McKibben Muscle
5.1. Contracting Force Model
5.2. Extracted Hysteresis Model
5.3. Elasticity Model
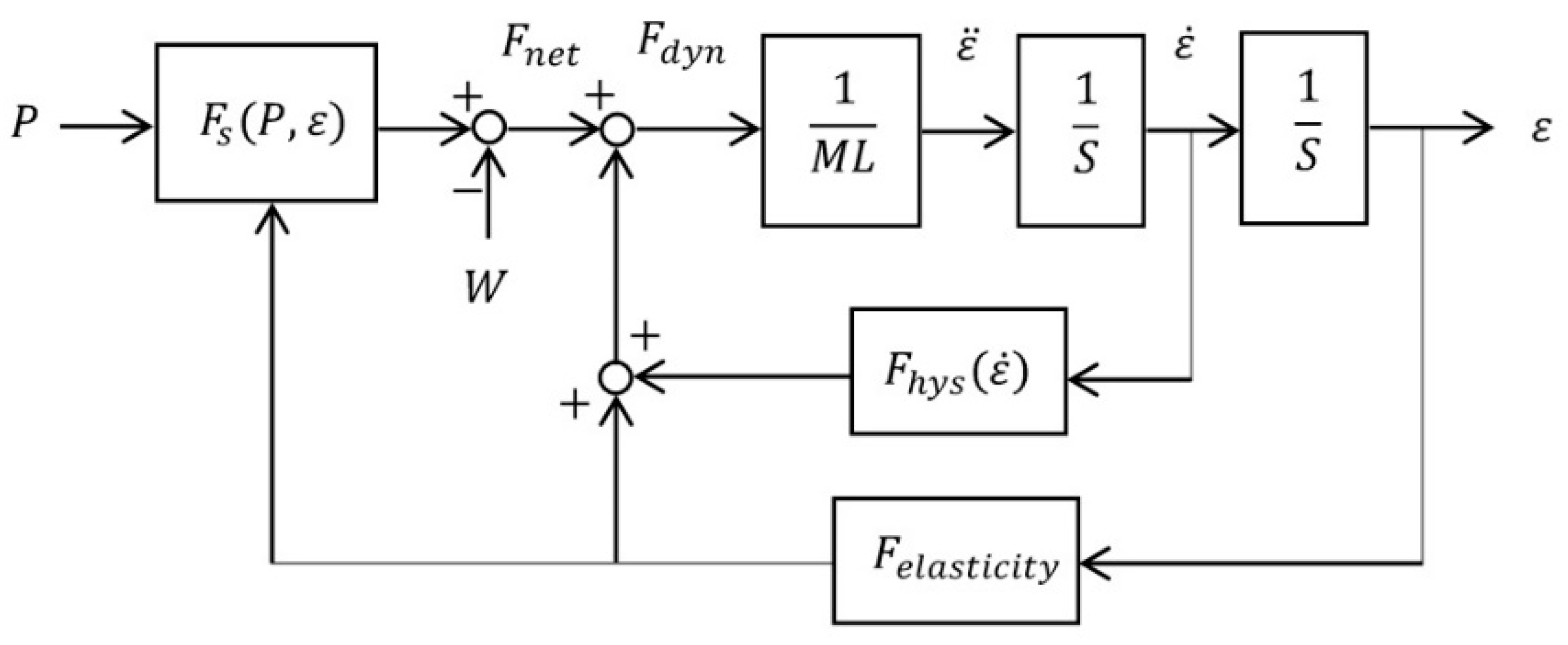
5.4. Dynamic Equation for Vertical Load System
6. Results
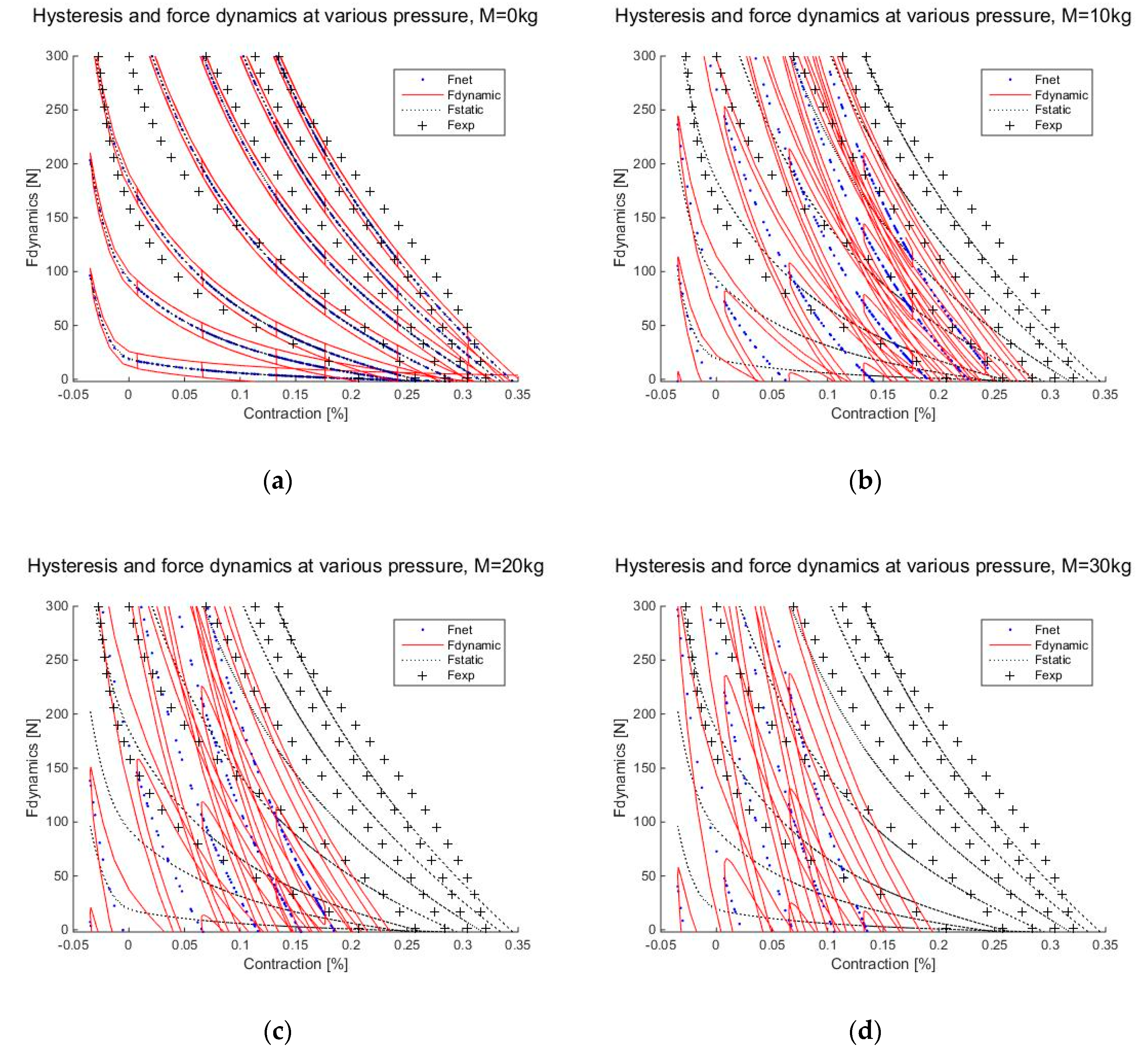
6.1. Force Dynamic Characteristics
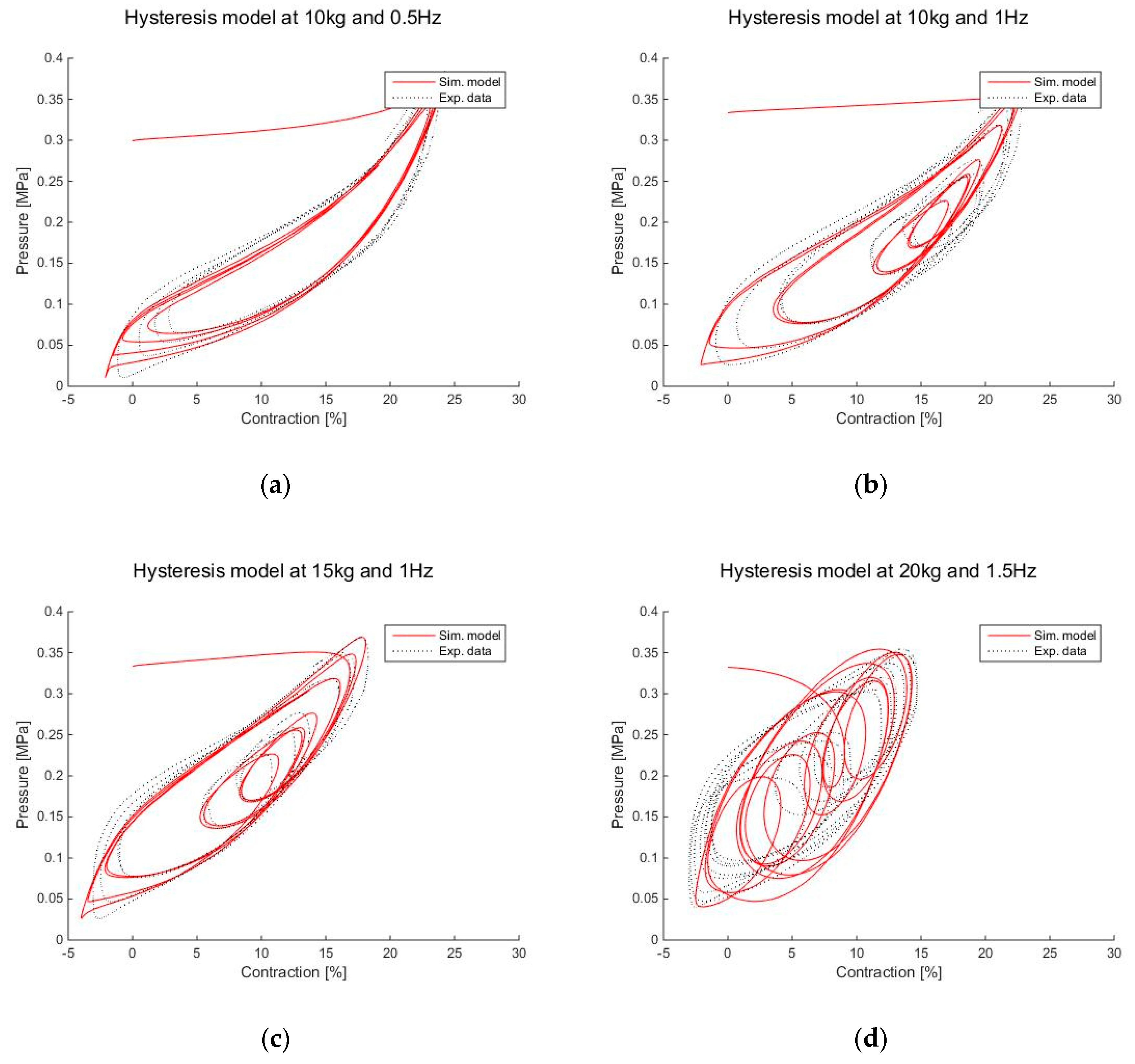
6.2. Empirical Model Simulation
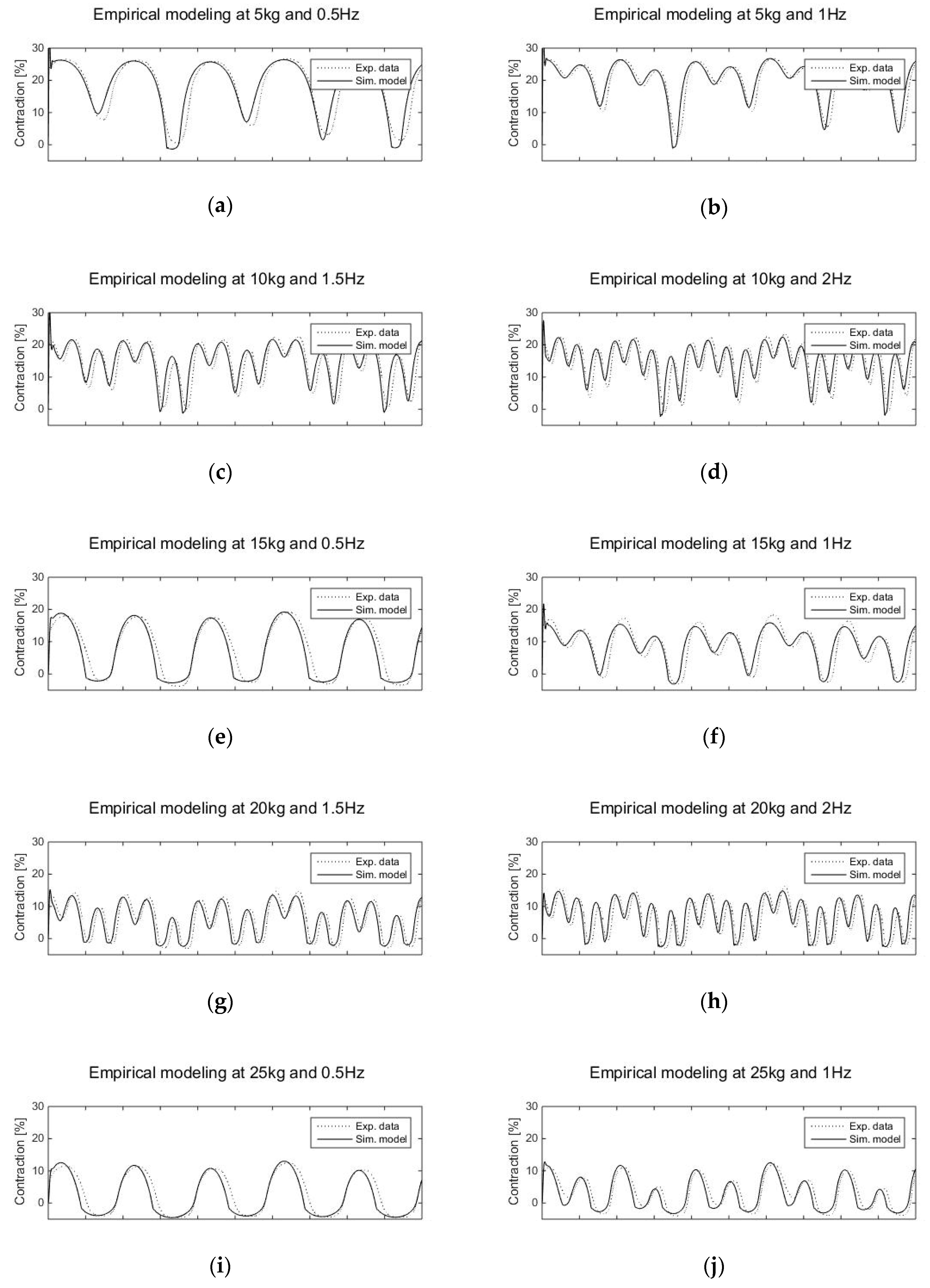
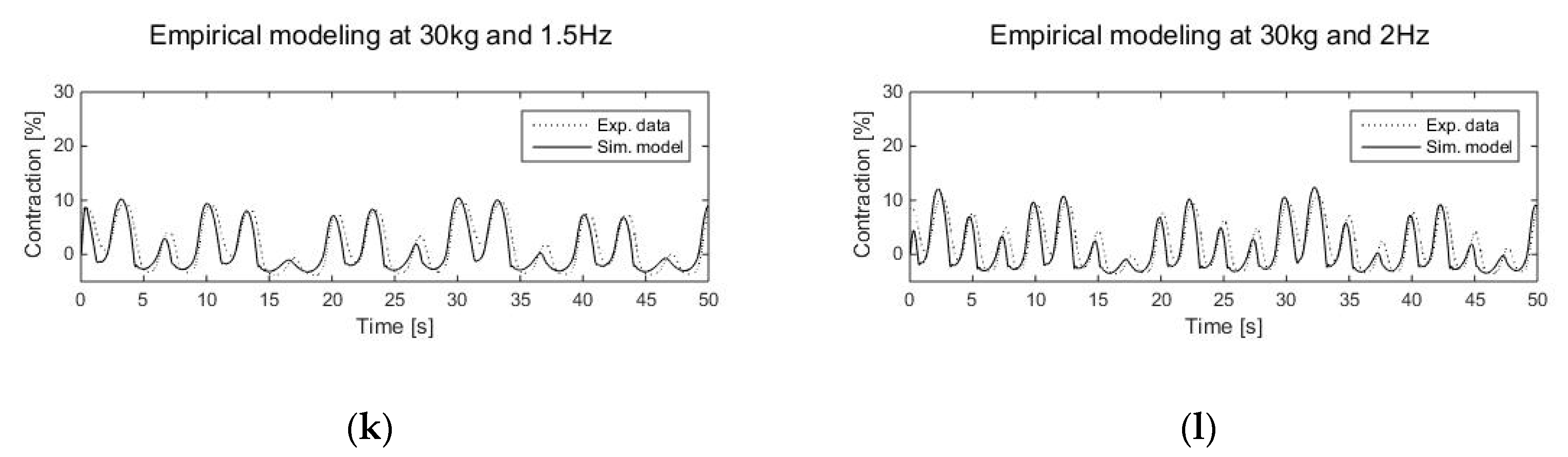
6.3. Empirical Model Testing
7. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dzahir, M.A.M.; Yamamoto, S.I. Recent trends in lower-limb robotic rehabilitation orthosis: control scheme and strategy for pneumatic muscle actuated gait trainers. Robotics 2014, 3, 120–148. [Google Scholar] [CrossRef]
- Dzahir, M.A.M.; Yamamoto, S.I. Design and Evaluation of the AIRGAIT Exoskeleton: Leg Orthosis Control for Assistive Gait Rehabilitation. J. Robot. 2013, 2013, 535106. [Google Scholar] [CrossRef]
- Zhang, Z.; Philen, M. Pressurized artificial muscles. J. Intell. Mater. Syst. Struct. 2011, 23, 255–268. [Google Scholar] [CrossRef]
- Kothera, C.S.; Jangid, M.; Sirohi, J.; Wereley, N.M. Experimental characterization and static modeling of McKibben actuators. J. Mech. Des. 2009, 131, 1–10. [Google Scholar] [CrossRef]
- Daerden, F.; Lefeber, D. The concept and design of pleated pneumatic artificial muscles. Int. J. Fluid Power 2001, 2, 41–50. [Google Scholar] [CrossRef]
- Daerden, F.; Lefeber, D. Pneumatic artificial muscles: Actuators for robotics and automation. Eur. J. Mech. Environ. Eng. 2002, 47, 10–21. [Google Scholar]
- Inoue, K. Rubbertuators and applications for robots. In Proceedings of the International Symposium on Robotics Research, Cambridge, MA, USA, 1988; pp. 57–63. [Google Scholar]
- Tondu, B.; Boiter, V.; Lopez, P. Naturally compliant robot-arms actuated by McKibben artificial muscles. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 2–5 October 1994; pp. 2635–2640. [Google Scholar]
- Reynolds, D.B.; Repperger, D.W.; Phillips, C.A.; Bandry, G. Modeling the dynamic characteristics of pneumatic muscle. Ann. Biomed. Eng. 2003, 31, 310–317. [Google Scholar] [CrossRef]
- Hildebrandt, A.; Sawodny, O.; Neumann, R.; Hartmann, A. Cascaded control concept of a robot with two degrees of freedom driven by four artificial pneumatic muscle actuators. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 680–685. [Google Scholar]
- Davis, S.; Tsagarakis, N.; Canderle, J.; Caldwin, D.G. Enhanced modelling and performance in braided pneumatic muscle actuators. Int. J. Robot. Res. 2003, 22, 213–227. [Google Scholar] [CrossRef]
- Davis, S.; Caldwin, D.G. Braid effects on contractile range and friction modeling in pneumatic muscle actuators. Int. J. Robot. Res. 2006, 25, 359–369. [Google Scholar] [CrossRef]
- Kerscher, T.; Albiez, J.; Zollner, J.M.; Dillmann, R. Evaluation of the dynamic model of fluid muscles using quick-release. In Proceedings of the IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, Pisa, Italy, 20–22 February 2006. [Google Scholar]
- Wickramatunge, K.C.; Leephakpreeda, T. Empirical modeling of pneumatic artificial muscle. In Proceedings of the International Multi-conference of Engineers and Computer Scientists, Hong Kong, China, 18–20 March 2009; Volume II. [Google Scholar]
- Wickramatunge, K.C.; Leephakpreeda, T. Study on mechanical behaviors of pneumatic artificial muscle. Int. J. Eng. Sci. 2010, 48, 188–198. [Google Scholar] [CrossRef]
- Krichel, S.V.; Sawodny, O.; Hildebrandt, A. Tracking control of a pneumatic muscle actuator using one servovalve. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 4385–4390. [Google Scholar]
- Kang, B.S.; Kothera, C.S.; Woods, B.K.S.; Wereley, N.M. Dynamic modeling of McKibben pneumatic artificial muscles for antagonistic actuation. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 182–187. [Google Scholar]
- Itto, T.; Kogiso, K. Hybrid modeling of McKibben pneumatic artificial muscle systems. In Proceedings of the IEEE International Conference on Industrial Technology, Auburn, AL, USA, 14–16 March 2011; pp. 65–70. [Google Scholar]
- Sarosi, J. Newest approach to modeling hysteresis in the force-contraction cycle of pneumatic artificial muscle. Acta Tech. Conviniensis Bull. Eng. 2012, 5, 63–66. [Google Scholar]
- Sarosi, J. Elimination of the hysteresis effect of PAM actuator: Modelling and experimental studies. Tech. Gaz. 2015, 6, 1489–1494. [Google Scholar]
- Tothova, M.; Pitel, J. Dynamic model of pneumatic actuator based on advanced geometric muscle model. In Proceedings of the IEEE International conference on Computational Cybernetics, Tihany, Hungary, 8–10 July 2013; pp. 83–87. [Google Scholar]
- Kulesza, Z. Isotonic characteristics of a pneumatic muscle actuator. Adv. Robot. 2014, 28, 833–840. [Google Scholar] [CrossRef]
- Nuchkrua, T.; Leephakpreeda, T. Actuation of pneumatic artificial muscle via hydrogen absorption/desorption of metal hydride. Adv. Mech. Eng. 2014, 7, 364306. [Google Scholar] [CrossRef]
- Yao, B.; Zhuo, Z.; Liu, Q.; Ai, Q. Empirical modeling and position control of single pneumatic artificial muscle. J. Control Eng. Appl. Inform. 2016, 18, 86–94. [Google Scholar]
- Ibadi, A.A.; Meziani, S.N.; Davis, S. Valuable experimental model of contraction pneumatic muscle actuator. In Proceedings of the IEEE International Conference on Methods and Models in Automation and Robotics, Miedzyzdroje, Poland, 29 August–1 September 2016; pp. 744–749. [Google Scholar]
- Ibadi, A.A.; Meziani, S.N.; Davis, S. Efficient structure-based models for the McKibben contraction pneumatic muscle actuator: The full description of the behavior of the contraction PMA. Actuators 2017, 6, 32. [Google Scholar] [CrossRef]
- Ibadi, A.A.; Meziani, S.N.; Davis, S. Design, implementation and modelling of the single and multiple extensor pneumatic muscle actuators. Syst. Sci. Control Eng. 2018, 6, 80–89. [Google Scholar] [CrossRef] [Green Version]
- Chou, C.P.; Hannaford, B. Measurement and modeling of McKibben pneumatic artificial muscles. IEEE Trans. Robot. Autom. 1996, 12, 90–102. [Google Scholar] [CrossRef]
- Tondu, B.; Lopez, P. Modeling and control of McKibben artificial muscle robot actuators. IEEE Control Syst. Mag. 2000, 20, 15–38. [Google Scholar]
- Colbrunn, R.W.; Nelson, G.M.; Quinn, R.D. Modeling of braided pneumatic actuators for robotic control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001. [Google Scholar]
- Schroder, J.; Erol, D.; Kawamura, K.; Dillmann, R. Dynamic pneumatic actuator model for a model-based torque controller. In Proceedings of the IEEE International Symposium on Computational intelligence in Robotics and Automation, Kobe, Japan, 16–20 July 2003; pp. 342–347. [Google Scholar]
- Balasubramanian, S.; Huang, H.; He, J. Quantification of dynamic property of pneumatic muscle actuator for design of therapeutic robot control. In Proceedings of the IEEE EMBS Annual International Conference, New York, NY, USA, 30 August–3 September 2006; pp. 2734–2737. [Google Scholar]
- Jouppila, V.; Gadsden, S.A. Modeling and identification of a pneumatic muscle actuator system controlled by an on/off solenoid valve. In Proceedings of the International fluid Power Conference, Aachen, Germany, 22–24 March 2010; pp. 1–11. [Google Scholar]
- Tang, R.; Liu, D. An enhanced dynamic model for McKibben pneumatic muscle actuators. In Proceedings of the Australasian Conference on Robotics and Automation, Wellington, New Zealand, 3–5 December 2012. [Google Scholar]
- Zhong, J.; Fan, J.; Zhu, Y.; Zhao, J.; Zhai, W. Static modeling for commercial braided pneumatic muscle actuators. Adv. Mech. Eng. 2014, 2014, 425217. [Google Scholar] [CrossRef]
- Iyer, R.V.; Tan, X. Control of hysteretic systems through inverse compensation. IEEE Control Syst. 2009, 29, 83–99. [Google Scholar] [CrossRef]
- Oh, J.H.; Bernstein, D.S. Semilinear Duhem model for rate-independent and rate-dependent hysteresis. IEEE Trans. Autom. Control 2005, 50, 631–645. [Google Scholar] [Green Version]
- Ramli, M.H.M.; Dzahir, M.A.M. A new phenomenological based rate-dependent hysteresis operator for hysteresis characterization. J. Mech. Eng. 2018, 5, 142–153. [Google Scholar]
- Ramli, M.H.M.; Minh, T.V.; Chen, X. Pseudoextended bouc-wen model and adaptive control design with applications to smart actuators. IEEE Trans. Control Syst. Technol. 2018, 99, 1–10. [Google Scholar] [CrossRef]
- Yoshida, H.; Kawata, K.; Fukuyama, Y.; Takayama, S.; Nakanishi, Y. A particle swarm optimization for reactive power and voltage control considering voltage security assessment. IEEE Trans. Power Syst. 2001, 99, 1232–1239. [Google Scholar]
- Gaing, Z.L. A particle swarm optimization approach for optimum design of PID controller in AVR system. IEEE Trans. Energy Convers. 2004, 19, 384–391. [Google Scholar] [CrossRef]
- Parsopoulos, K.E.; Vrahatis, M.N. Recent approaches to global optimization problems through Particle Swarm Optimization. Nat. Comput. 2002, 1, 235–306. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, L.; Qian, J.; Ma, L. Robust PID controller design using particle swarm optimizer. In Proceedings of the IEEE International Symposium on Intelligent Control, Houston, TX, USA, 5–8 October 2003. [Google Scholar]
- Beielstein, T.B.; Parsopoulos, K.E.; Vrahatis, M.N. Design and analysis of optimization algorithms using computational statistics. Appl. Num. Anal. Comp. Math. 2004, 1, 413–433. [Google Scholar] [CrossRef]
- Zhao, J.; Li, T.; Qian, J. Application of particle swarm optimization algorithm on robust PID controller tuning. Proceeding of the International Conference on Natural Computation, Changsha, China, 27–29 August 2005; pp. 948–957. [Google Scholar]
- Hu, H.; Hu, Q.; Lu, Z.; Xu, D. Optimal PID controller design in PMSM servo system via particle swarm optimization. In Proceedings of the Annual Conference of IEEE Industrial Electronics Society, Raleigh, NC, USA, 6–10 November 2005. [Google Scholar]
- Markos, S.; Kamal, H. Optimal tuning of PID controller using adaptive hybrid particle swarm optimization algorithm. Int. J. Comput. Commun. Control 2012, 7, 101–114. [Google Scholar]
- Ikhouane, F.; Rodellar, J. A linear controller for hysteretic systems. IEEE Trans. Autom. Control 2006, 51, 340–344. [Google Scholar] [CrossRef]
- Mayergoyz, I. Mathematical models of hysteresis. IEEE Trans. Magn. 1986, 22, 603–608. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Kiong, K. Advanced Control of Piezoelectric Micro-/Nanopositioning Systems; Springer: New York, NY, USA, 2016. [Google Scholar]
- Minh, T.V.; Tjahjowidodo, T.; Ramon, H.; Brussel, H.V. A new approach to modeling hysteresis in a pneumatic artificial muscle using the Maxwell-slip model. IEEE/ASME Trans. Mechatron. 2011, 16, 177–186. [Google Scholar] [CrossRef]

| Population size, | 50 |
| Number of generations, | 10 |
| Velocity constant, | 1.5 |
| Velocity constant, | 1.5 |
| Variable | Description | Variable | Description |
|---|---|---|---|
| Input pressure | Rate dependency correction function | ||
| Contracting length, velocity and acceleration | Dynamic force | ||
| Initial braid angle | Static force | ||
| Mass of the weight | Hysteretic force | ||
| Gravitational acceleration | Coulomb friction | ||
| Initial diameter | Viscous friction | ||
| Initial length and length | Net force | ||
| Coefficient of elasticity (PSO) | Elastic force | ||
| Constant coefficients (PSO) | Number of population | ||
| Coulomb and viscous friction coefficients | Number of generation | ||
| Shape irregularity correction function | Velocity constants | ||
| Slenderness correction function | Local optimum | ||
| Load dependency correction function | Global optimum |
| Quasi-Static\Rate | 0.5 Hz | 1 Hz | 1.5 Hz | 2 Hz |
|---|---|---|---|---|
| 5 kg | 0.929 | 0.894 | 0.815 | 0.732 |
| 10 kg | 0.937 | 0.903 | 0.825 | 0.739 |
| 15 kg | 0.952 | 0.883 | 0.847 | 0.763 |
| 20 kg | 0.955 | 0.898 | 0.839 | 0.741 |
| 25 kg | 0.941 | 0.895 | 0.853 | 0.797 |
| 30 kg | 0.948 | 0.904 | 0.861 | 0.799 |
| 0.944 ± 0.009 | 0.897 ± 0.007 | 0.843 ± 0.016 | 0.752 ± 0.027 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mat Dzahir, M.A.; Yamamoto, S.-i. Dynamic Modeling of McKibben Muscle Using Empirical Model and Particle Swarm Optimization Method. Appl. Sci. 2019, 9, 2538. https://doi.org/10.3390/app9122538
Mat Dzahir MA, Yamamoto S-i. Dynamic Modeling of McKibben Muscle Using Empirical Model and Particle Swarm Optimization Method. Applied Sciences. 2019; 9(12):2538. https://doi.org/10.3390/app9122538
Chicago/Turabian StyleMat Dzahir, Mohd Azuwan, and Shin-ichiroh Yamamoto. 2019. "Dynamic Modeling of McKibben Muscle Using Empirical Model and Particle Swarm Optimization Method" Applied Sciences 9, no. 12: 2538. https://doi.org/10.3390/app9122538
APA StyleMat Dzahir, M. A., & Yamamoto, S.-i. (2019). Dynamic Modeling of McKibben Muscle Using Empirical Model and Particle Swarm Optimization Method. Applied Sciences, 9(12), 2538. https://doi.org/10.3390/app9122538