Efficient Weights Quantization of Convolutional Neural Networks Using Kernel Density Estimation based Non-uniform Quantizer

Abstract

Convolutional neural networks (CNN) have achieved excellent results in the field of image recognition that classifies objects in images. A typical CNN consists of a deep architecture that uses a large number of weights and layers to achieve high performance. CNN requires relatively large memory space and computational costs, which not only increase the time to train the model but also limit the real-time application of the trained model. For this reason, various neural network compression methodologies have been studied to efficiently use CNN in small embedded hardware such as mobile and edge devices. In this paper, we propose a kernel density estimation based non-uniform quantization methodology that can perform compression efficiently. The proposed method performs efficient weights quantization using a significantly smaller number of sampled weights than the number of original weights. Four-bit quantization experiments on the classification of the ImageNet dataset with various CNN architectures show that the proposed methodology can perform weights quantization efficiently in terms of computational costs without significant reduction in model performance.

1. Introduction

In the field of image recognition, various types of deep learning models based on CNN have been proposed and achieved excellent results [1,2,3,4,5]. A typical CNN model consists of several convolution layers that extract features of input data and fully-connected layers that perform classification from feature maps. Through such a structure, CNN records superior performance exceeding human classifying ability, but there is trade-off. CNN consists of very deep layers to extract the features of input data, and the number of weights used in each layer is very large. In other words, despite its excellent performance, the deep learning model has high computational costs. For example, AlexNet has about 60 million parameters with 8 layers and VGGNet-16 consists of about 138 million parameters with 16 layers. As there is a lot of computation from input to output in these deep learning models, for a mobile or embedded device with insufficient memory space or power, it is difficult to distribute the deep learning model for various applications.

In order to efficiently train CNN architectures, which are composed of multiple layers, a graphics processing device capable of performing operations with a lot of weights and gradients is indispensably required. In contrast, when only the forward propagation is performed to apply the pre-trained CNN, the hardware restriction is relatively free. Nevertheless, forward propagation of CNN is also problematic for applications in mobile and embedded hardware devices because it requires a large amount of computation between input data and numerous weights. First, the manufacturing of high-performance embedded hardware capable of performing large-scale tasks requires relatively high production cost. Second, the high computational costs of the deep learning model make it difficult to apply the model in the real-time environment, and increase the energy consumption of the device. Therefore, it is important to reduce the computational costs in order to apply the CNN model with high performance in such an environment.

Weights quantization is one of the potential solutions to this situation. In the past, various neural network quantization methodologies have been studied to make digital hardware implementation easier [6]. The recently proposed quantization studies of deep learning model are not only focused on simplifying the hardware implementation but further reducing the computational costs while maintaining the performance of the original model. For example, in FPGA based hardware, it is possible to develop a more efficient deep learning model application device by reducing the number of multipliers required for the operation [7]. By reducing the bit size of the weights from the neurons to the neurons, the number of FPGA based hardware multipliers that actually perform calculations can be reduced. As a result, the power efficiency of the hardware can be increased, and the computational efficiency of real-time applications of the object recognition model in the embedded environment can be increased.

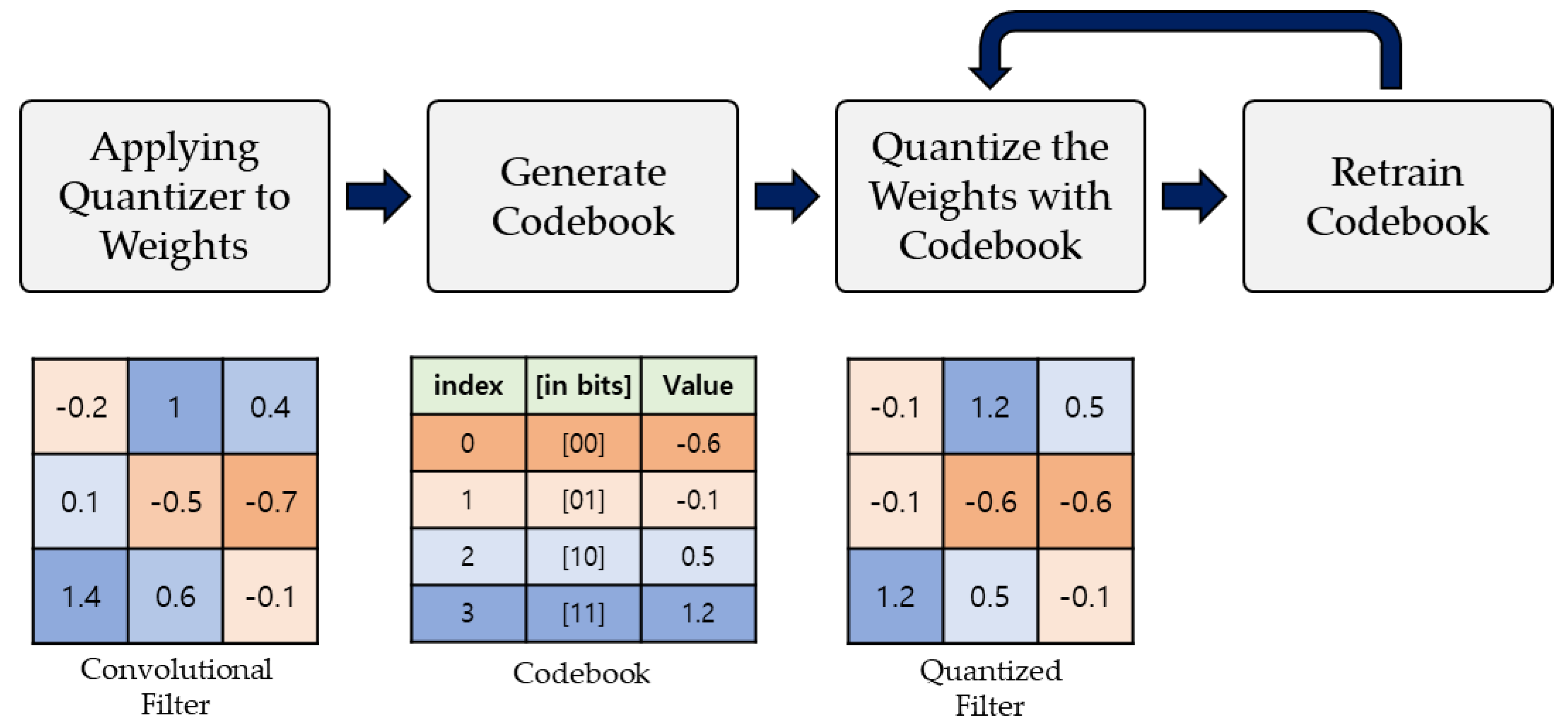
Figure 1 shows the general weights quantization process for the CNN model. In this process, clustering for the pre-trained weights of CNN is performed first and then a codebook of weights is created. The size of the codebook is determined by the target bit-width of quantization. When a codebook is generated through a quantizer, the original weights are mapped to an index of the codebook having the closest value to the original weights. Through this process, we can obtain quantized weights that have smaller bandwidth compared to that of 32-bit float type weights. This process is referred to as weights quantization, and it enables more efficient application of various deep learning models. Recent studies related to weights quantization attempt to restore the performance of the deep learning model in the quantization process, including the retraining process as well as the quantization [8,9].

General weights quantization methodologies with retrain have some disadvantages. First, because codebook generation and retraining are usually performed repeatedly, it takes a lot of time to construct the final quantized model [8]. This problem is a limitation when we want to deploy the quantized model quickly. The existing approaches usually use non-uniform quantization rather than uniform quantization in order to minimize the loss of performance inherent in quantization, even though it involves retrain processes [8,9,10]. In general, non-uniform quantization methods including k-means are often applied to the weights quantization of neural networks [8,9,10,11,12,13]. However, the simple k-means have a problem because it takes a lot of time to reconstruct a codebook. Because the range of weights is not wide and weights have similar values, to perform distance calculations for all the weights is not efficient.

In this paper, we utilize kernel density estimation to obtain the probability density function of pre-trained weights of CNN. Then we perform sampling through the previously obtained probability density function, and non-uniform quantization is applied on those sampled data. The contribution of this paper is summarized as follows.

• The existing weights quantization methodology is inefficient in terms of computational costs. We propose a method that performs quantization more efficiently by using kernel density estimation and sampled data from the probability density function.
• A number of recent studies on weights quantization have focused on the recovery of lost performance through retrain phase. The proposed methodology can perform fast quantization suitable for this retrain phase and fast deployments.
• We compare the performance of CNN weights quantization using quantization methodologies such as uniform quantization, Lloyd–Max quantizer, and k-means clustering.
• Experiments on various CNN architectures such as AlexNet, VGGNet, and ResNet show that the proposed methodology can be widely applied to various CNN architectures.

2. Related Works

2.1. Weights Quantization of Deep Learning Model

Compression of the neural network requires a set of methodologies to reduce the size of the architecture and the weights of the neural network, while maintaining the original performance as much as possible. There are CNN architectures designed for use in mobile and embedded devices. First, SqueezeNet has similar accuracy to AlexNet, but the size of the weights is about 1/50 [14]. SqueezeNet proposes a fire module configured to the squeeze layer and the expansion layer utilizing a 1x1 convolution filter to design a tight architecture. Similarly, MobileNet allows forward propagation at a faster speed by applying a method such as a depth-wise separable convolution [15].

There are two main approaches in quantization of neural network weight. The first is to quantize the weights of neural networks in the training phase, the other is to quantize the weights of the trained neural networks. BinaryConnect is a typical way of doing quantization during the training phase [16]. BinaryConnect is a forward and backward propagation that enables the use of binarized weights. This method has the property of using the sign function to binarize the weights in the forward process and to hold the real-valued weights in the backpropagation process. XNOR-Net has attempted to use binary weights of neural networks for classifying large datasets such as ImageNet [17]. XNOR-Net improves the training and inference efficiency by binarizing weights and the input data, along with gradients. Based on these studies, DoReFa-Net uses binarized weights, binarized activation, and binarized gradients up to an arbitrary bit width. This method improved the performance of XNOR-Net using a sophisticated rounding mechanism [18].

On the other hand, deep compression is a typical method of quantizing the connection weights of neural networks learned [8]. Deep compression is a three stage pipeline that can reduce the memory requirements of the network from 35 to 49 times without degrading the accuracy by applying the quantization Huffman coding technique. The method first removes the value of the unaffected connection to zero and performs the quantization. After the retrain, the lost performance is restored and the quantization process is repeated a predetermined number of times. Finally, Huffman coding is applied to connection weights so that it is possible to efficiently store connection weights with a high frequency. Deep compression achieves high compression rates in this way while maintaining good performance. Entropy-constrained scalar quantization (ECSQ) was designed to quantize using the k-means clustering methodology to minimize loss of the neural network as well as the quantization error by applying a hessian matrix [19]. Incremental networks quantization (INQ) efficiently reduces the loss caused by quantization by performing three independent operations of weights partitioning, quantization, and retrain [9]. This methodology combines the benefits of quantization during training with the benefits of quantization after training compared to other quantization methods.

In addition, the quantization methodology to minimize the energy consumption of the model using fixed point weights has been proposed [20]. WAGE trains the model by quantizing all elements such as weights, activation, gradients, and error, which adjust the range or set of weights [21]. In addition, various methods of weights quantization of neural networks, including retraining and so on, are being studied [22,23,24,25,26]. Based on these studies, a quantization codebook has been applied to LCNN [27]. Through LCNN, the quantized weights are then stored in a codebook that can be designed to enable more efficient inference using a lookup table.

2.2. Scalar Quantization

Quantization generally means dividing the data into finite levels by transformations and assigning specific values to each level. Among them, scalar quantization is the most basic form of the quantization methods that maps a data to a specific value in the codebook. This scalar quantization is distinguished by the types of intervals in the codebook—uniform or non-uniform. Uniform quantization is a method using quantization intervals which are the same size within a certain range. For example, there is a method of setting the size of the quantization interval by dividing the minimum and maximum values for specific input data by the quantization level.

$$Q_{step}=\left(X_{max}-X_{min}\right)/L$$

(1)

$$Q_{index}\left(X\right)=⎣\left(X-X_{min}\right)/Q_{step}⎦$$

(2)

$$Q\left(X\right)=Q_{index}\left(X\right)\ast Q_{step}+\frac{Q_{step}}{2}+ X_{min}$$

(3)

Quantization step-size $Q_{step}$ can be calculated using the desired quantization level $L$ and the maximum range of weights as in Equation (1). The quantized index $Q_{index}\left(X\right)$ of each weight can be obtained by calculating the number of quantization steps apart from the minimum value $X_{min}$ of weights as shown in Equation (2). Finally, using Equation (3), the quantized vector $Q\left(X\right)$ can be obtained as the center value of each quantization interval. The actual quantization is done by replacing $X$ with $Q\left(X\right)$. Uniform quantization allows very fast quantization for a given data, but there is a constraint that the distribution of input data must be uniform. In other words, when the distribution of input data is Gaussian distribution, Laplace distribution, or a special distribution such as a gamma distribution, the relative quantization error by using a uniform quantization method can become a loss of performance in CNN.

An alternative to this is non-uniform quantization. In non-uniform quantization the value is shifted in order to reduce the quantization error, and the intervals between quantization values are not uniform. Therefore, more sophisticated quantization with relatively low quantization error compared to uniform quantization can be expected. Representative non-uniform quantization is the Lloyd–Max quantizer and k-means clustering. Both of them try to minimize the mean squared error between the original value and the quantized value.

The Lloyd–Max quantizer adjusts the quantization value so that the area of the probability density function is the same for each quantization step. Optimized through this approach, the Lloyd–Max quantizer has a dense quantization step in areas with high probability density and, conversely, a wide quantization step in areas with low probability density.

$$\begin{array}{cc}\hfill D=\mathbb{E}\left[{\left(x-Q\left(x\right)\right)}^2\right]& = \underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\mathbb{E}\left[{\left(x-Q\left(x\right)\right)}^2\right]f\left(x\right)d\left(x\right)\hfill \\ & ={\displaystyle {\displaystyle \sum }_{i=1}^L}\underset{-b_{i-1}}{\overset{b_i}{{\displaystyle \int }}}\mathbb{E}[{\left(x-q_i\right)}^2]f\left(x\right)d\left(x\right)\hfill \end{array}$$

(4)

$$b_i=\frac{q_i+q_{i+1}}{2}$$

(5)

$$q_i=\frac{{{\displaystyle \int }}_{b_i}^{b_{i+1}}x{f}_x\left(x\right)dx}{{{\displaystyle \int }}_{b_i}^{b_{i+1}}{f}_x\left(x\right)dx}$$

(6)

The Lloyd–Max quantizer adjusts the values of boundary $b_i$ and quantized value $q_i$ so that the mean squared error between the original weights and the quantized weights are minimized, as shown in Equation (4). The two values in Equations (5) and (6) can be obtained by applying a Lagrange condition to Equation (4), $\frac{\partial D}{\partial b_i}=0$, $\frac{\partial D}{\partial q_i}=0$.

Another representative methodology for non-uniform quantization is the k-means clustering. Quantization through k-means clustering is one of the main methodologies for quantizing weights of CNN. The quantization using k-means sets the number of quantization bits to ${\log }_{2}k$, and based on the result of clustering, the data of each cluster is mapped to the center value of the cluster.

$$\underset{C}{\mathrm{argmin}}{\displaystyle \sum }_{i=1, {\mu }^i\in M,c^i}^k{\displaystyle \sum }_{w_j^i\in W,c^i}\Vert {\mu }^i-w_j^i\Vert {}^2$$

(7)

Equation (7) is the objective of k-means clustering methodology. This method sets the size of k to $2^q$ where q is the number of quantization bits, and clusters the weights to minimize the mean square error between the ${\mu }^i$, which is the centroid of cluster $c^i$ and each weight $w_j^i$ in the same cluster $c^i$. $M$ is the set of cluster centroids and W is the set of all original weights.

By using non-uniform quantization methods, we can expect a relatively high performance of the quantized CNN model because the quantization is performed in the direction in which the quantization error is reduced. However, because both the Lloyd–Max quantizer and the k-means clustering method described above are based on iteration, there is a problem that the computation time is increased depending on the size of the input data.

2.3. Kernel Density Estimation

From a probabilistic point of view, data is a specification of one of the various possibilities of a particular random variable. As one piece of data is only a part of a random variable, a large number of data is needed to understand the overall appearance of the random variable. In general, the method of estimating the distribution characteristics of the original random variable from the distribution of observed data is called density estimation. Estimating the characteristics of a random variable $X$ is equivalent to estimating the probability density function of that variable. For example, when there is a probability density function $f\left(X\right)$ of a random variable $X$, $f\left(X=a\right)$ refers to a relative likelihood that $X$ has the value of $a$.

Density estimation methods can be divided into parametric and non-parametric methods. The simplest method of non-parametric density estimation is the histogram representation. This is a way of expressing the frequency of a given data divided by a specific bin. However, histograms have a discontinuity at the boundaries of the histogram bin, and this is a disadvantage in high dimensional data where the bins are different according to the size and the starting position.

Parametric density estimation uses the pre-defined model of the probability density function and estimates the parameters of the model from the data. The kernel density estimation is one of the parametric density estimation methods that solves the problem of the histogram method by using the kernel function. There are two general conditions for the kernel function. One is that it should be symmetric about the origin and non-negative, and the other is that the summation of the integral should be 1. For example, Gaussian, Epanechinkv, and Uniform are typical kernel functions.

$$f\left(x\right)=\frac{1}{nh}{\displaystyle \sum }_{i=1}^{n}K\left(\frac{x_i-x}{h}\right)$$

(8)

In Equation (8), the $h$ which controls the size of the neighborhood around $x$ is the smoothing parameter. The function $K$ is called the kernel which controls the weight given to the observations $x_i$ at each point $x$ based on their proximity. Therefore, it can control the shape of the probability distribution. The kernel function $f(·)$ for the observed data $x$ can make the probability density function by summing all these kernel functions and dividing them by the total number of the data. The estimated probability density function reflects the characteristics of the observed data. By using this function, it is possible to sample new data from a distribution of observed data.

3. Kernel Density Estimation based on Non-Uniform Quantization

3.1. Overview of the Proposed Quantization Process

The non-uniform quantization methodology is suitable for performing weights quantization of CNN because it optimizes to reduce quantization errors. However, one of the key features of deep learning models like CNN is the large number of weights. For k-means, the amount of computations increases proportionally as the number of weights increases. In particular, because the k-means is one of the NP-hard problems, it is difficult to proceed until convergence, and by placing an upper limit on optimization, the results of quantization with relatively low performance can be obtained by early stopping. Similarly, the Lloyd–Max quantizer is affected by the number of data when performing an integrated calculation in the actual computing environment. As the range of weights in the pre-trained deep learning model is relatively small and a lot of weights have similar values, it is inefficient to obtain quantized values for all weights to reflect the characteristics of the weights. This paper proposes a kernel density estimation based non-uniform quantization that can be more efficient in terms of computation time.

Figure 2 shows an overview of the suggested kernel density estimation based non-uniform quantization methodology. First, weights from a pre-trained CNN are used to perform the kernel density estimation to make a probability density function about the original weights. By using this probability density function, we can sample the data reflecting characteristics of original weights. At this point, the number of sampled data is smaller than the number of original weights, enabling more efficient quantization operations. Through sampled data, k-means quantization becomes more efficient in terms of computation. Similarly, the sampled data are used again for kernel density estimation and make a probability density function of data. The Lloyd–Max quantizer using the probability density function of sampled data is more efficient in the integral computation, because the number of sampled data used to calculate the area of the probability distribution function is much smaller than the number of original weights.

K-means use sampled data in the probability density function of the original data, and the Lloyd–Max quantizer performs the kernel density estimation on the sampled data and uses the probability function of the sampled data. The k-means and Lloyd–Max quantizer of the proposed methodology are separately performed. Therefore, each methodology independently generates a codebook to carry out quantization of the originals.

3.2. Kernel Density Estimation based K-means Quantization (KDE-KM)

The proposed kernel density estimation based k-means quantization (KDE-KM) obtains the probability density function by performing the kernel density estimation from the original weights. The KDE-KM is then performed using sampled data from the probability density function that has the same characteristics of the original data, and it is possible to quantize more efficiently because it performs calculations on a much smaller number of data. Below is the pseudocode of the proposed KDE-KM methodology.

Algorithm 1. KDE-KM

Input:$W^o$, $q_{bit}$, $N$, $E$     original weights $W^o$, target quantization bit $q_{bit}$, the number of sampling data $N$,     the number of maximum iteration $E$ Output:$W^q$     quantized weights $W^q$ Initialization:$K$, $C$, $M$     The number of cluster $K$ = $2^{q_{bit}}$, clusters $C=\left\{c^1, c^2, \dots , c^k\right\}$,     cluster centroids $M=\left\{{\mu }^1,{\mu }^2, \dots , {\mu }^k\right\}$   1:   $PD{F}^o\leftarrow KDE\left(W^o\right)$    // kernel density estimation using original weights   2:   $D^s\leftarrow PD{F}^o$($N$)                //sampling $N$ data using probability density function   3:   for e = 1 to $E$ do   4:    $c^j$ $\leftarrow$ $\underset{c^j }{\mathrm{argmin}}\Vert {\mu }^j-d_i\Vert {}^2$, for $d_i\in D^s$        // assign $D^s$ to clusters in $C$   5:    for j = 1 to $K$ do   6:     ${\mu }^j\leftarrow \frac{1}{\left|c^j\right|}{\displaystyle \sum }_{i=1}^{\left|c^j\right|}{d}_i^j$, where $d_i^j\in D^s,c^j$   // update cluster centroids $M$   7:    $c^j$ $\leftarrow$ $\underset{c^j }{\mathrm{argmin}}\Vert {\mu }^j-w_i^o\Vert {}^2$, for all $w_i^o\in W^o$   // assign all original weights $W^o$ to a cluster   8:   for j = 1 to $K$ do   9:    for i = 1 to $\left|c^k\right|$ do 10:      $w_i^j$ $\leftarrow {\mu }^j$, where $w_i^j\in W^o, c^j$           // quantize the original weights $W^o$ 11:   $W^q\leftarrow$ $W^o$                            // set quantized weights $W^q$ 12:   return $W^q$

Algorithm 1 shows the proposed KDE-KM process. The proposed method estimates the $PD{F}^o$ from the original weights $W^o$ and then $PD{F}^o$ samples a set of sampled data $D^s$ by using the number of samples $N$, which is less than the number of original weights $W^o$. The proposed method can reduce the time complexity of quantization by using sampled data $D^s$. In this case, $K$ is set to $2^{q_{bit}}$. After the clustering is finished, it assigns all the original weights $W^o$ to a specific cluster $c^i$, and assigns ${\mu }^i$, which is the cluster centroid of $c^i$ as the quantization value to the original weights to get $W^q$.

3.3. Kernel Density Estimation Based Lloyd–Max Quantizer (KDE-LM)

The proposed kernel density estimation based Lloyd–Max quantizer (KDE-LM) builds the quantizer in a manner similar to the k-means using sampled data. KDE-LM minimizes quantization errors by repeatedly minimizing the difference in area separated by quantization values in the probability density function by adjusting the quantization values. At this point, if the number of weights increases, the computational costs for the correct integral computation also heavily increases. Therefore, by performing a kernel density estimation once again using relatively small number of sampled data, and quantizing using it, quantization can be performed more efficiently in terms of the number of operations. Below is the pseudocode of the proposed KDE-LM methodology.

Algorithm 2. KDE-LM

Input:$W^o$, $q_{bit}$, $N$, $E$     original weights $W^o$, target quantization bit $q_{bit},$ the number of sampling data $N$,     the number of maximum iteration $E$ Output: $W^q$     quantized weights $W^q$ Initialization: $K$, $Q$     The number of quantization value $K=2^{q_{bit}}$,     quantization values $Q$$=\left\{q_1, q_2, \dots , q_K\right\}$   1:   $PD{F}^o\leftarrow KDE\left(W^o\right)$    // kernel density estimation using original weights   2:   $D^s\leftarrow PD{F}^o\left(N\right)$        // sampling $N$ data using probability density function   3:   $PD{F}^s\leftarrow KDE\left(D^s\right)$     // kernel density estimation using sampled data   4:   for e = 1 to $E$ do   5:    for i = 1 to $K-1$ do   6:     $b_i= \frac{q_i+q_{i+1}}{2}$   7:     $q_i=\frac{{{\displaystyle \int }}_{b_i}^{b_{i+1}}xPD{F}^s{}_x\left(x\right)dx}{{{\displaystyle \int }}_{b_i}^{b_{i+1}}PD{F}^s{}_x\left(x\right)dx}$   8:   for i = 1 to $\left|W^o\right|$ do   9:    $w_i^o\leftarrow \underset{q_j }{\mathrm{argmin}}\Vert w_i^o-q_j\Vert {}^2$, where $w_i^o\in W^o$    // quantize the original weights $W^o$ 10:   $W^q$ $\leftarrow$ $W^o$                 // set quantized weights $W^q$ 11:   return $W^q$

Algorithm 2 shows the proposed KDE-LM process. Similar to KDE-KM, KDE-LM uses the KDE for original weights $W^o$. However, KDE-LM has a difference in that it performs KDE once more from sampled data $D^s$ to get the $PD{F}^s$. The advantage of using sampled data $D^s$ and the $PD{F}^s$ is less computation costs when performing integral computation at line 7. The quantization is performed by assigning the quantization value to the original weights through line 9.

4. Experiments

4.1. Experimental Setup

Experiments were conducted without retraining on pre-trained CNN and we measured the accuracy of classifying 1000 classes using the 50,000 validation images of the ImageNet dataset [28]. The weights quantizations using the proposed KDE-KM and KDE-LM were performed on AlexNet, VGGNet, ResNet, which are well-known in the field of image classification [1,2,4]. Then the accuracy of the 4-bit quantized model using Uniform, KDE-KM, and KDE-LM were compared to the accuracy of the reference model using 32-bit float type weights. Additionally, the proposed methodology’s sampling ratio was measured indicating how many less weights were used to perform quantization compared to the number of existing original weights. In all experiments, the size of the sampled data was fixed to 10,000. The number of sampled data used in the quantization was divided by the number of weights of all the networks. The reference models used were pre-trained models in the pytorch framework.

4.2. Performance Evaluations on Quantized CNN Architecutres

We quantized the weights of AlexNet, VGGNet-16, and ResNet-18 using a total of three quantizers. The first model uses a uniform quantizer, which sets the uniform quantization step in the range of minimum and maximum values. The second model is a KDE-LM quantizer using probability density function of sampled data. Finally, we tested the performance of KDE-KM quantizer using sampled data from the probability density function of the original weights. The proposed models perform non-uniform quantization by using fewer data to improve efficiency.

Table 1. Performance comparison of AlexNet architecture.

Model	Bit-Width	Top-1 Accuracy (%)	Top-5 Accuracy (%)	$\mathbf{Sampling}\mathbf{Ratio}(\frac{\left|{\mathit{W}}_{\mathit{s}}\right|}{\left|{\mathit{W}}_{\mathit{t}}\right|})$
Reference	32	56.52	79.07	1.0
Uniform	4	6.48	15.99	1.0
KDE-LM (ours)	4	41.25	66.16	0.0013
KDE-KM (ours)	4	47.43	72.1	0.0013

,

Table 2. Performance comparison of VGGNet-16 architecture.

Model	Bit-Width	Top-1 Accuracy (%)	Top-5 Accuracy (%)	$\mathbf{Sampling}\mathbf{Ratio}(\frac{\left|{\mathit{W}}_{\mathit{s}}\right|}{\left|{\mathit{W}}_{\mathit{t}}\right|})$
Reference	32	71.55	90.33	1.0
Uniform	4	39.46	63.81	1.0
KDE-LM (ours)	4	66.16	86.38	0.0012
KDE-KM (ours)	4	67.76	88.14	0.0012

and

Table 3. Performance comparison of ResNet-18 architecture.

Model	Bit-Width	Top-1 Accuracy (%)	Top-5 Accuracy (%)	$\mathbf{Sampling}\mathbf{Ratio}(\frac{\left|{\mathit{W}}_{\mathit{s}}\right|}{\left|{\mathit{W}}_{\mathit{t}}\right|})$
Reference	32	69.73	89.04	1.0
Uniform	4	1.05	3.53	1.0
KDE-LM (ours)	4	58.39	81.48	0.0154
KDE-KM (ours)	4	61.82	83.89	0.0154

represent bit-width, top-1 and top-5 accuracy, and sampling ratio of each quantized model for each CNN architecture.

The reference CNN models in the experiment perform operations with the weights of the 32-bit float type. In comparison, the quantized CNN models in the experiment perform operations with the weights of 4-bits. The experiment was conducted based on 4-bit quantization because existing quantization related studies reported relatively stable quantization up to a 5-bit band-width [26].

First, for the Uniform quantization, it recorded relatively very low accuracy compared to the reference model except for VGGNet-16. It can be seen that the classification is rarely performed correctly, especially for ResNet-18.

In contrast, in the case of the proposed KDE-LM and KDE-KM, they maintain competitive performance despite the 4-bit quantization. Given the performance difference between KDE-LM and KDE-KM, KDE-KM generally performs better with quantization. KDE-LM carries out quantization using the probability density function obtained by conducting the kernel density estimation once more on the sampled data, so it seems that more errors are introduced during sampling and estimation.

The typical k-means method clusters $d$-dimensional data of length $n$ into $k$ clusters through $i$ iterations. Thus, the time complexity of general k-means is $O\left(dnki\right)$. In the weights quantization task, $k$ and $d$ do not have much effect on time complexity. As the number of clusters $k$ is set to $2^q$ where $q$ is usually 8-bit or less, and each weight is a scalar rather than a vector, the time complexity of quantization using k-means is $O\left(ni\right)$. However, since the typical CNN uses a large number of weights, the value of $n$ is huge. Applying KDE-KM can greatly reduce the number of weights $n$ to $s$ ($s\ll n$), so it becomes $O\left(si\right)$, and because the number of iterations $i$ are also affected by the number of data, the time for the weights quantization can be reduced more than proportional to the sampling ratio. Likewise, because the Lloyd–Max quantizer needs an integral calculation to obtain the certain area of the probability density function, the amount of computation for the integral also increases as the number of weights increases. Therefore, applying KDE-LM can also reduce the computation costs for weights quantization proportional to the sampling ratio.

The ratio between sampled dataset and original weights set is presented in Table 1, Table 2 and Table 3 as the sampling ratio. The size of all sampled data was fixed at 10k data, and so the sampling ratio was 0.0013, 0.0012, and 0.0154 in AlexNet, VGGNet-16, and ResNet-18, respectively. This shows that similar accuracy to the reference model can be achieved using only 0.1% to 1% of original weights. These findings enable more efficient quantization when the quick quantization process is required in retraining, or when rapid deployments of a quantized model is required under certain circumstances.

4.3. Visualization of Quantized Convolutional Neural Networks

One of the important features of the proposed methodology is to perform kernel density estimation using the originals weights, and sampling from the resulting probability density function. Therefore, it is very important to perform the kernel density estimation efficiently using the characteristics of the distribution in the originals.

Figure 3 is the result of visualizing the distribution of the original weights and the sampled data together with the distribution of the quantized weights through the proposed KDE-KM, for the first two CNN architecture cases.

The first and third rows of Figure 3 are histograms of the weights of the first and second convolution layer, respectively. The distribution of original weights is shown in blue, and the histogram shown in red on top of them indicates the distribution of data sampled from the estimated probabilities density. Although there are a few discrepancies in certain areas, it can be seen that overall the distribution characteristics of the original weights and sampled data are consistent.

Next, the second and fourth rows of Figure 3 are the quantization results of the proposed KDE-KM methodology that are used to generate the codebook. It shows that the spacing of high density areas is narrow and the spacing of low density areas is relatively wide. These visualization results confirm that the proposed methodology is estimates the distribution of the original weights well, while at the same time performing non-uniform quantization successfully.

Figure 3 is the histogram of the entire weights in each convolution layer. So, it is difficult to determine what changes in each weight actually occur when quantization is performed. Figure 4 shows the nine filters of the AlexNet’s first convolution layer and the activated feature maps obtained from those filters.

In Figure 4, (b) is the original filters and (c) is the 4-bit quantized filters using the proposed KDE-KM. Using input image (a) and filters (b) and (c), activated feature maps (d) and (e) are obtained. The position of filters and feature maps are matched. In the upper right filter emphasized by red boxes in (b) and (c), we can see the difference of the adjacent weights in the quantized filter more clearly in (c). Accordingly, the upper right feature map highlighted by red boxes in (d) and (e) also shows that the contrast is relatively prominent in the feature map in (e), which is from the quantized filter. However, the original filter and the quantized filter show only a slight difference, and the feature maps obtained from each filter also show no significant differences.

5. Conclusions

Deep learning models such as CNN consist of many layers and have a very large number of weights. Due to the computation cost, it is difficult to apply them to a mobile or embedded device with insufficient memory or power, and weights quantization is one of the potential solutions.

Non-uniform quantization methodology such as k-means clustering and the Lloyd–Max quantizer are needed for more accurate quantization. However, recent deep learning models have a very large number of weights, so it is inefficient to perform non-uniform quantization with all the weights in the model. In particular, the speed of the quantization is important when the retraining is performed repeatedly, or when rapid deployment is required. In this paper, it was shown that the kernel density estimation can be used to perform quantization rapidly up to 4-bit without a significant decrease in accuracy, by using a very small number of weight samples of 0.13% to 1.5%.

In future studies, we plan to conduct further studies on the quantization of deep learning modes, including the retraining methodology applied to the quantization to restore the classification accuracy, the efficient quantization method for extreme low bit-width, and the application of quantization to other deep learning models for various tasks such as RNN or LSTM.