Non-Classical Model of Dynamic Behavior of Concrete
Abstract
:Featured Application
Abstract
1. Introduction
2. Model of Concrete
2.1. General Concept of the Model
2.2. Yield Surface
2.3. Dynamic Strength Criterion
2.4. Plastic Potential Function
2.5. Strain Rate Decomposition
2.6. Non-Associated Flow Rule
2.7. Evolution Parameter
2.8. Degradation of Modulus of Elasticity
2.9. Incremental Constitutive Relations
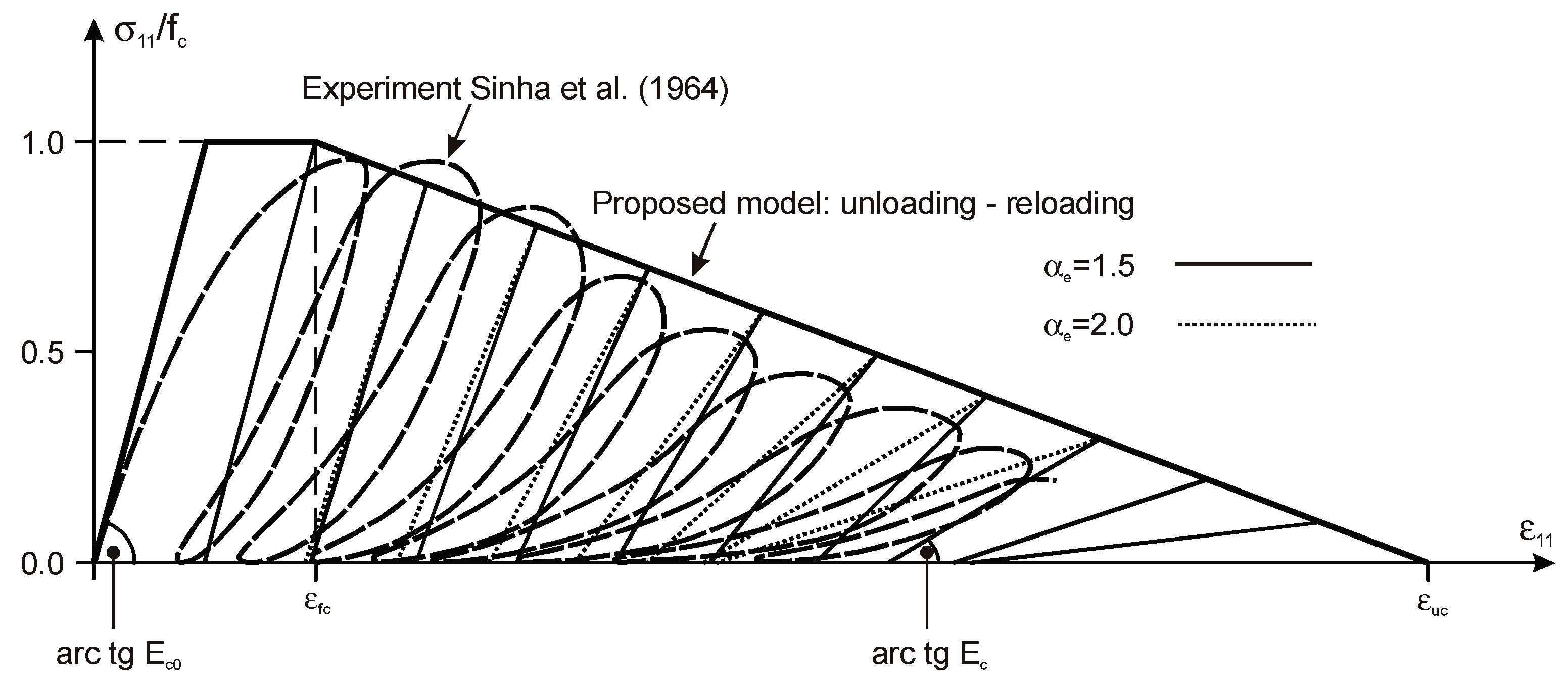
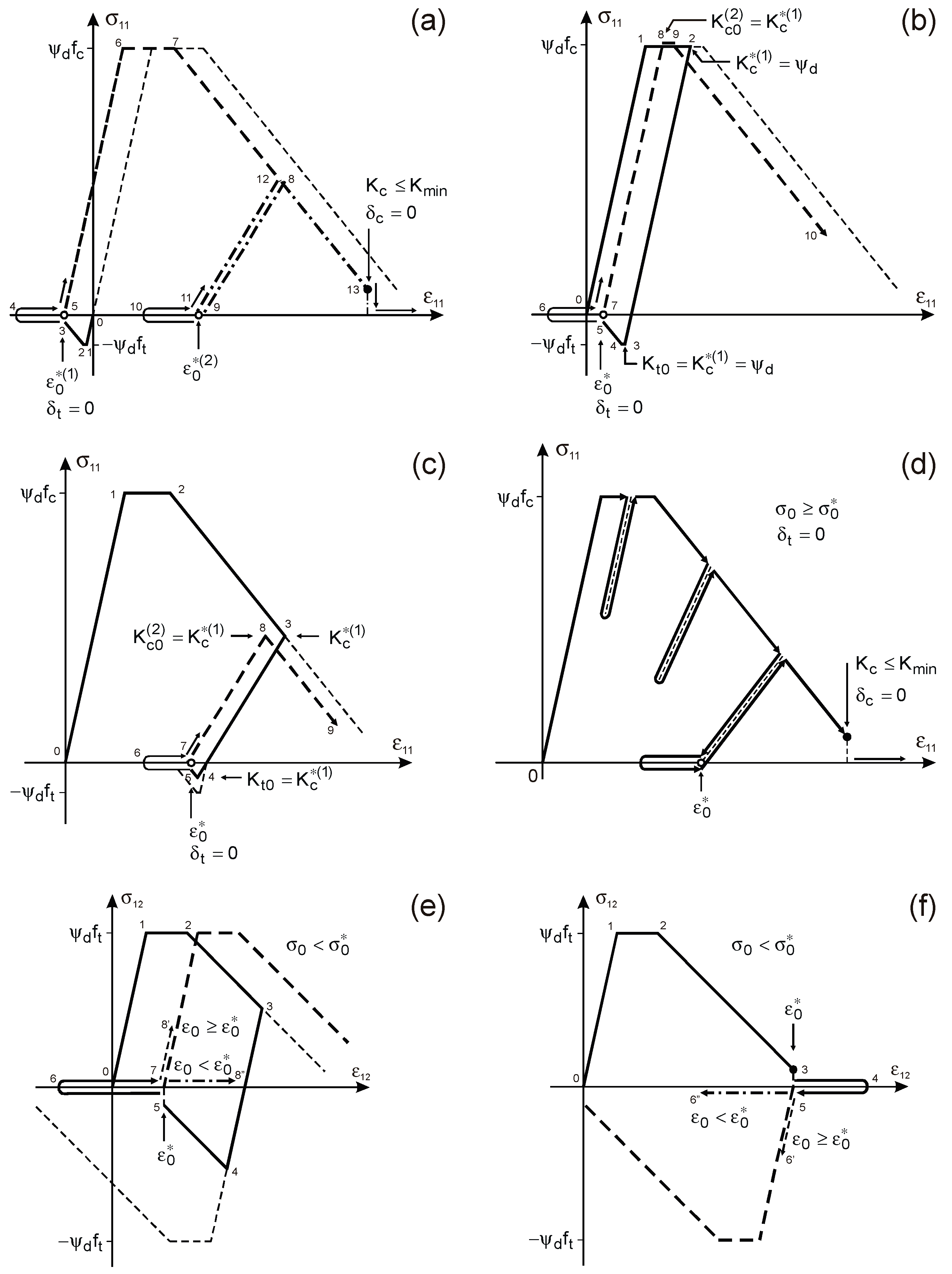
2.10. Elastic–Plastic Loading Process
2.11. Cracking and Crushing Mechanism
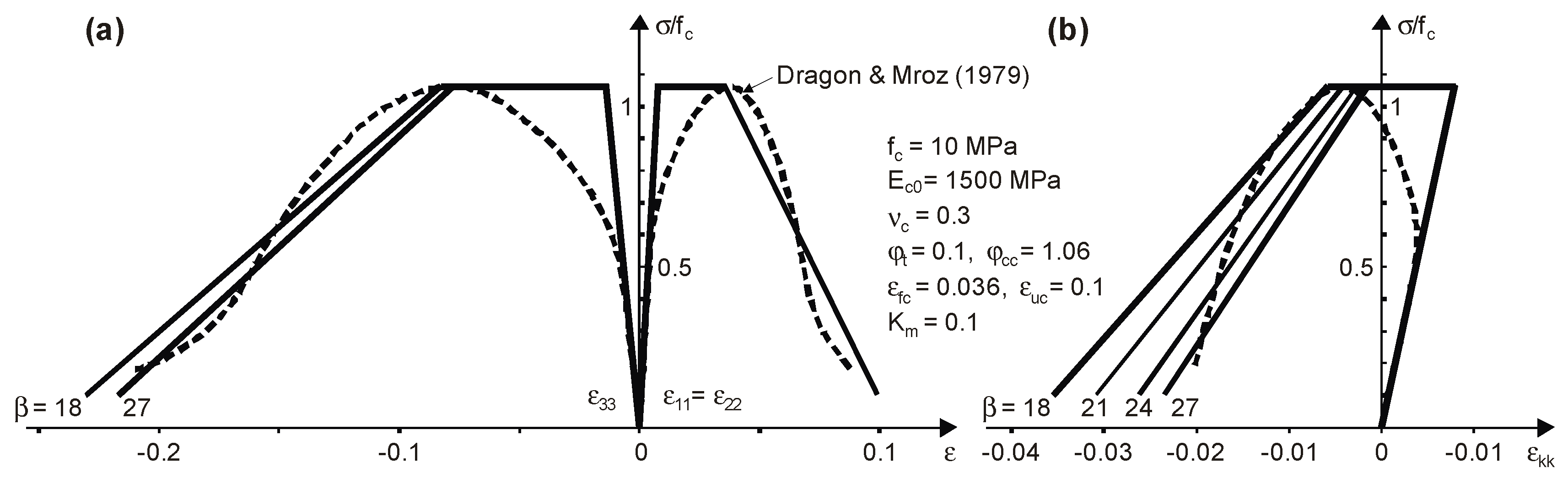
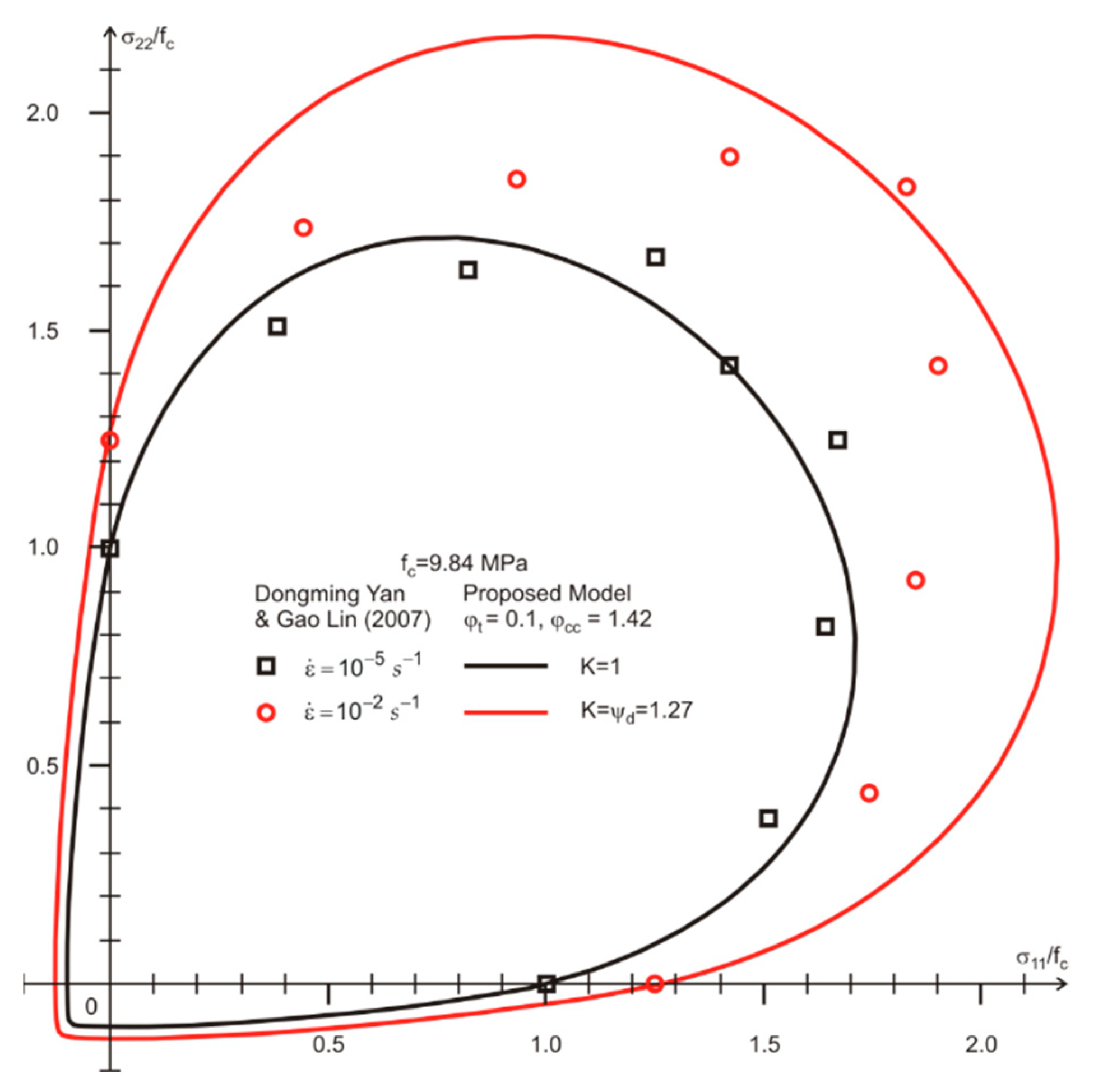
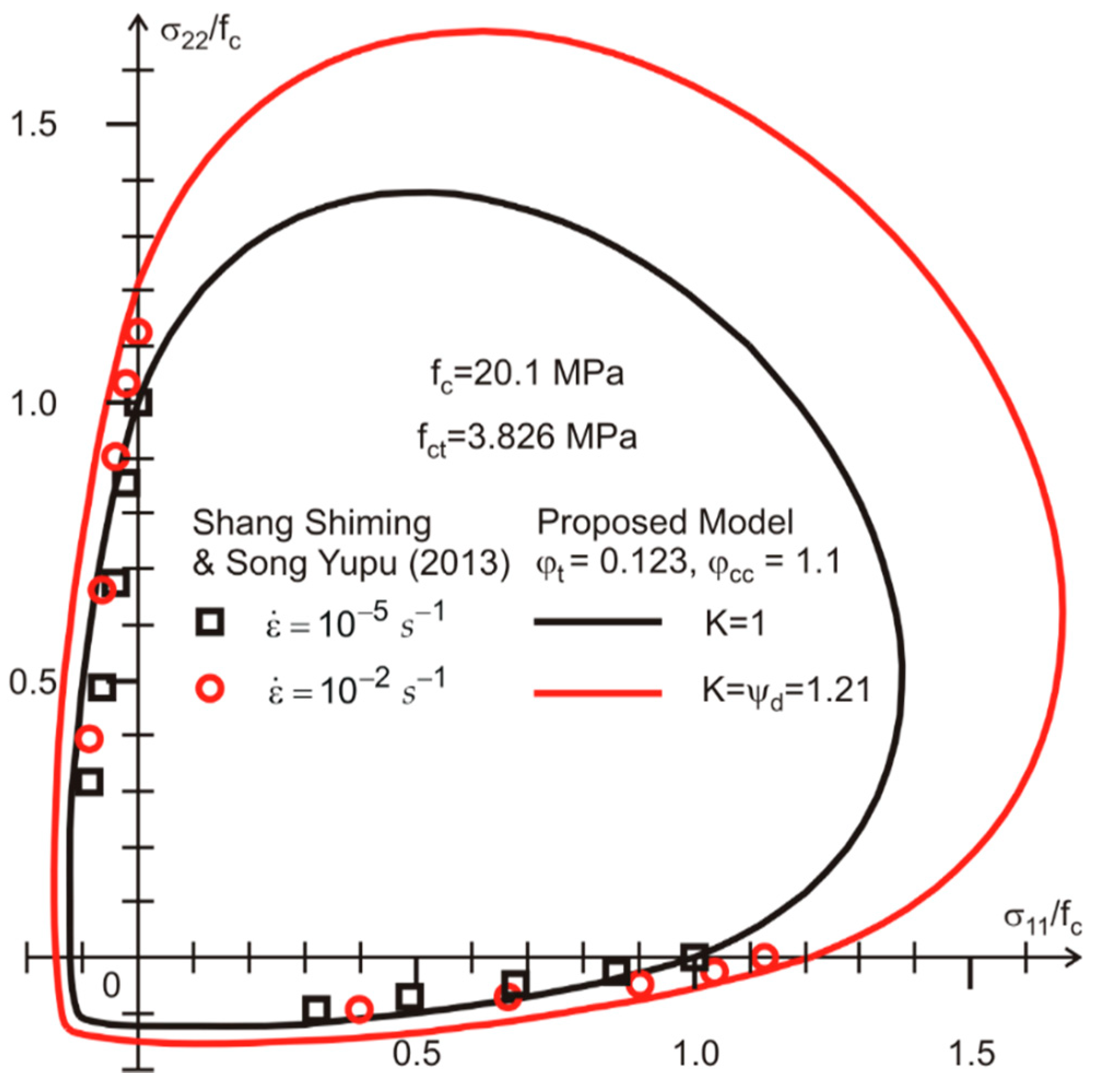
3. Comparative Analysis
3.1. Assumptions for Analysis
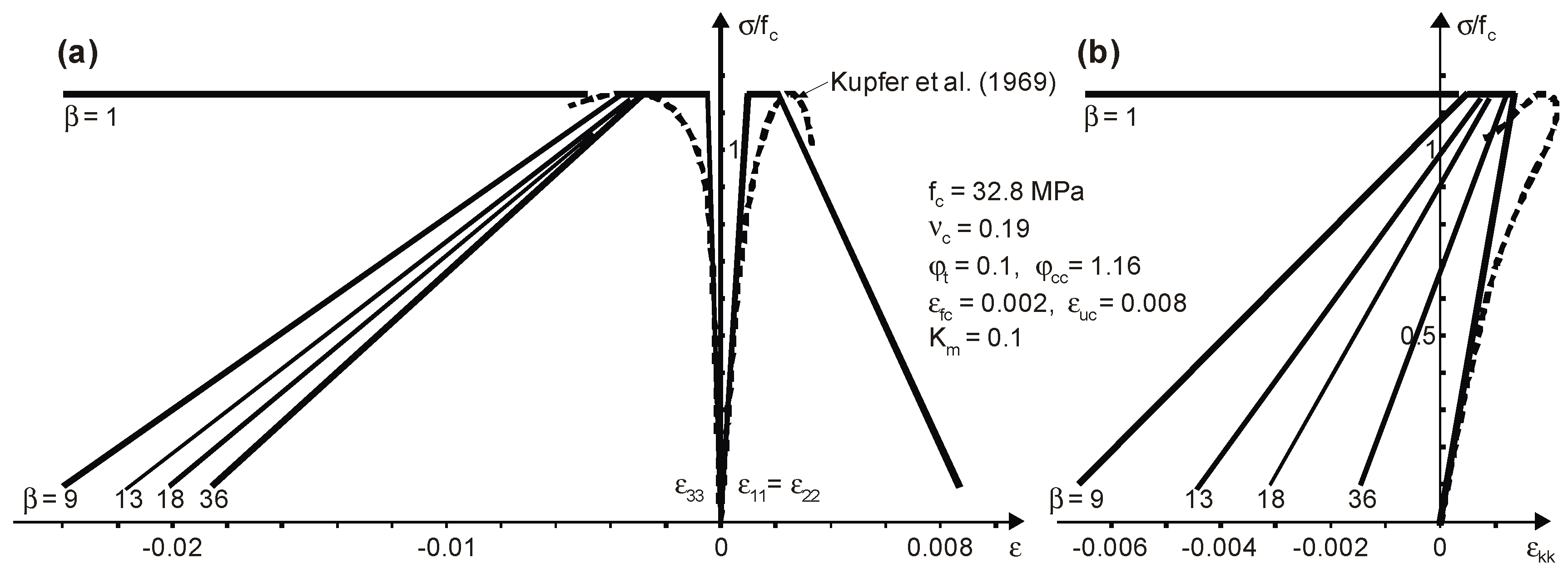
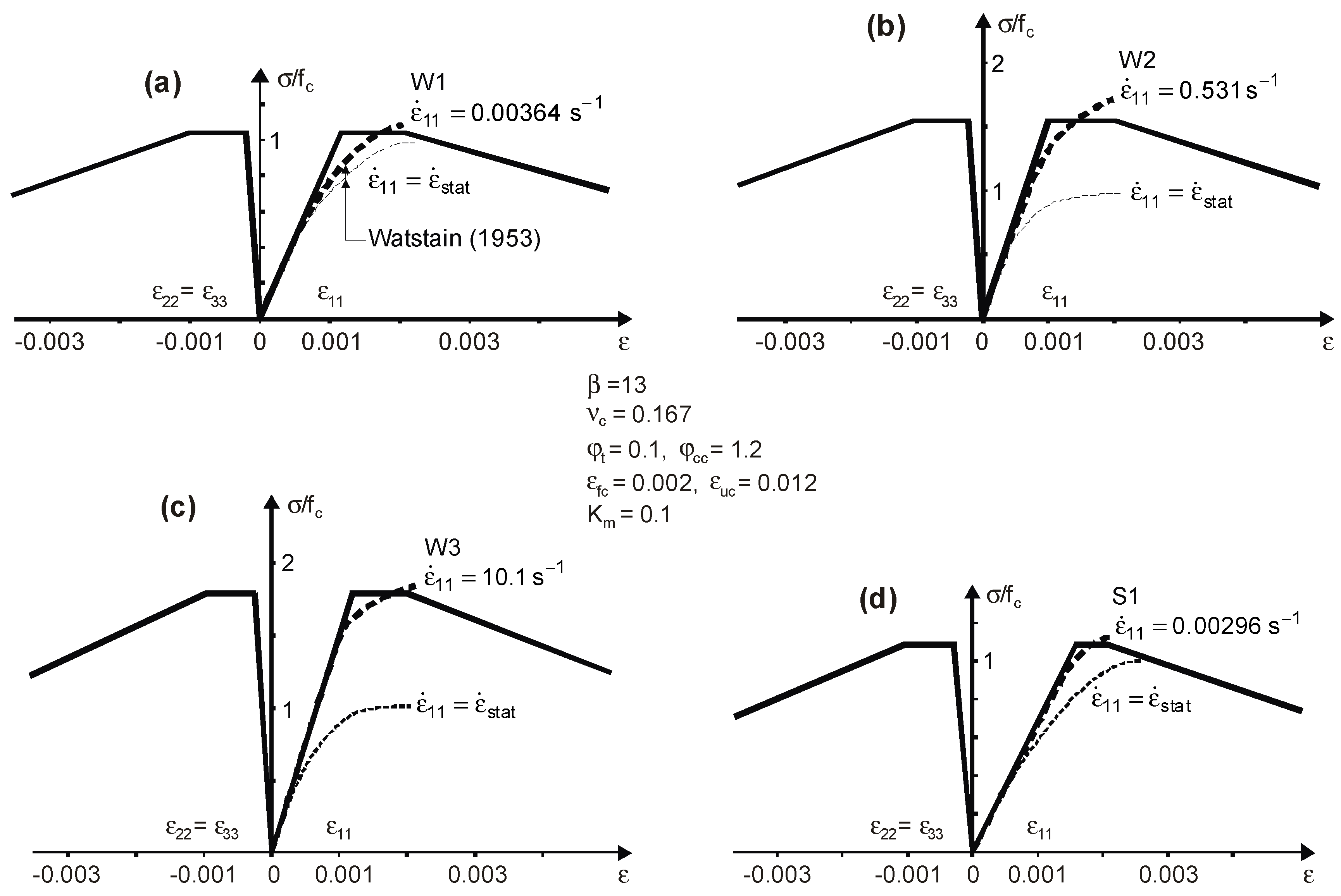
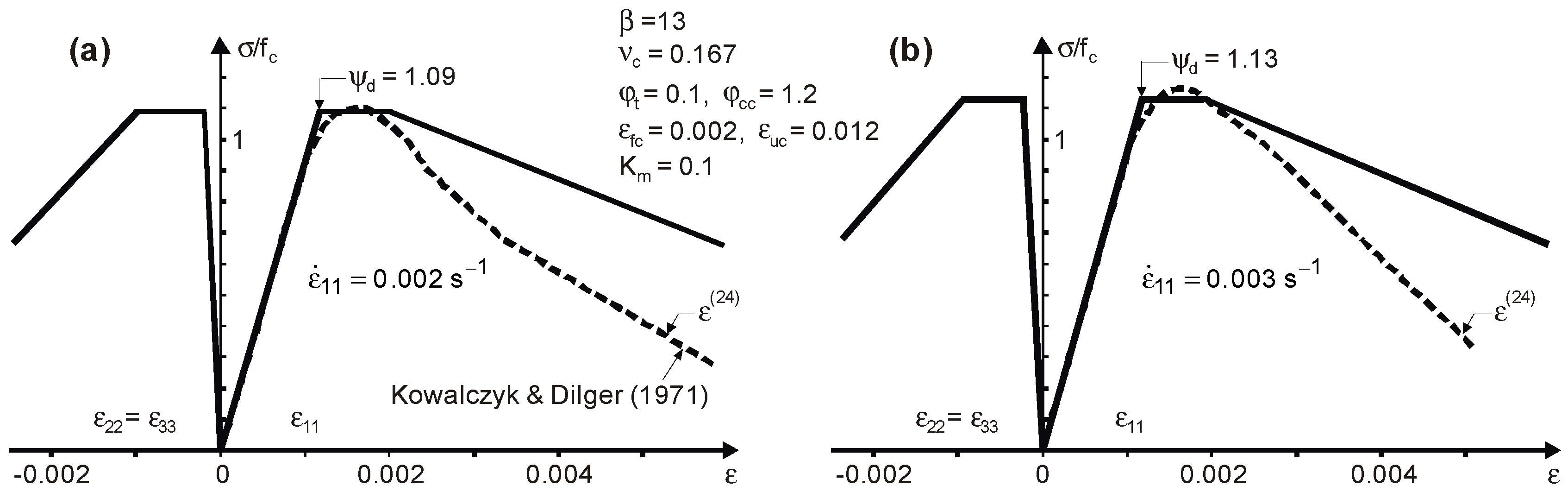
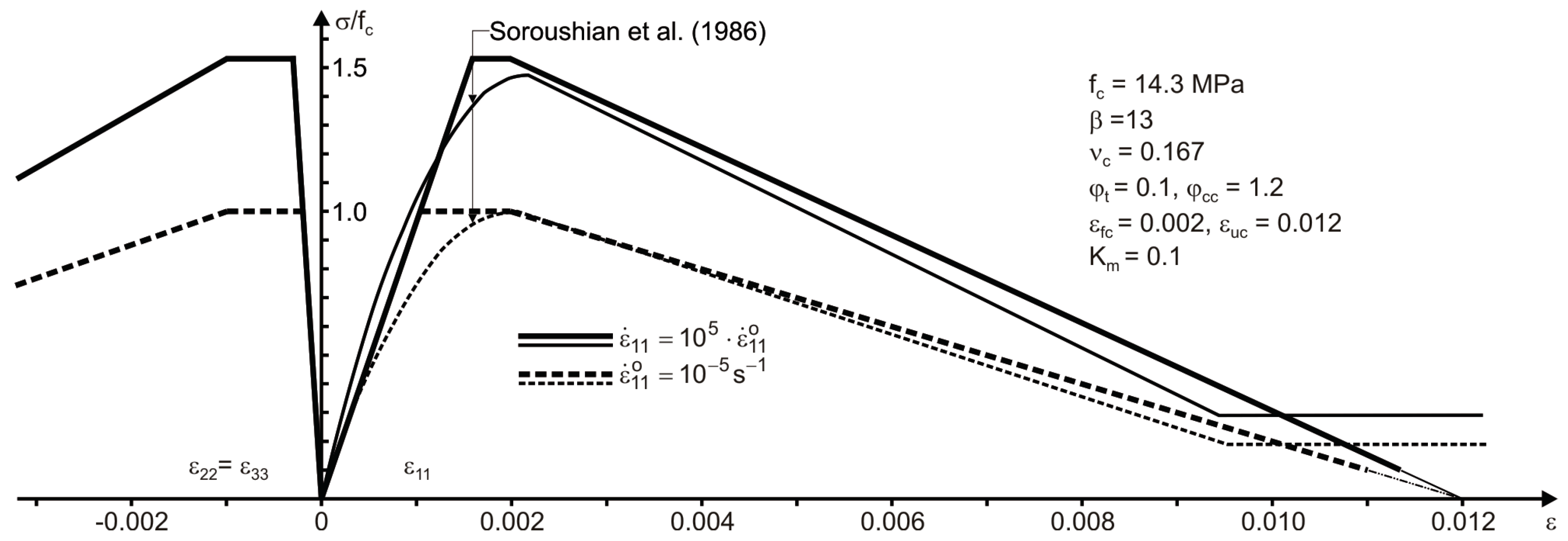
3.2. Comparisons for Static Tests
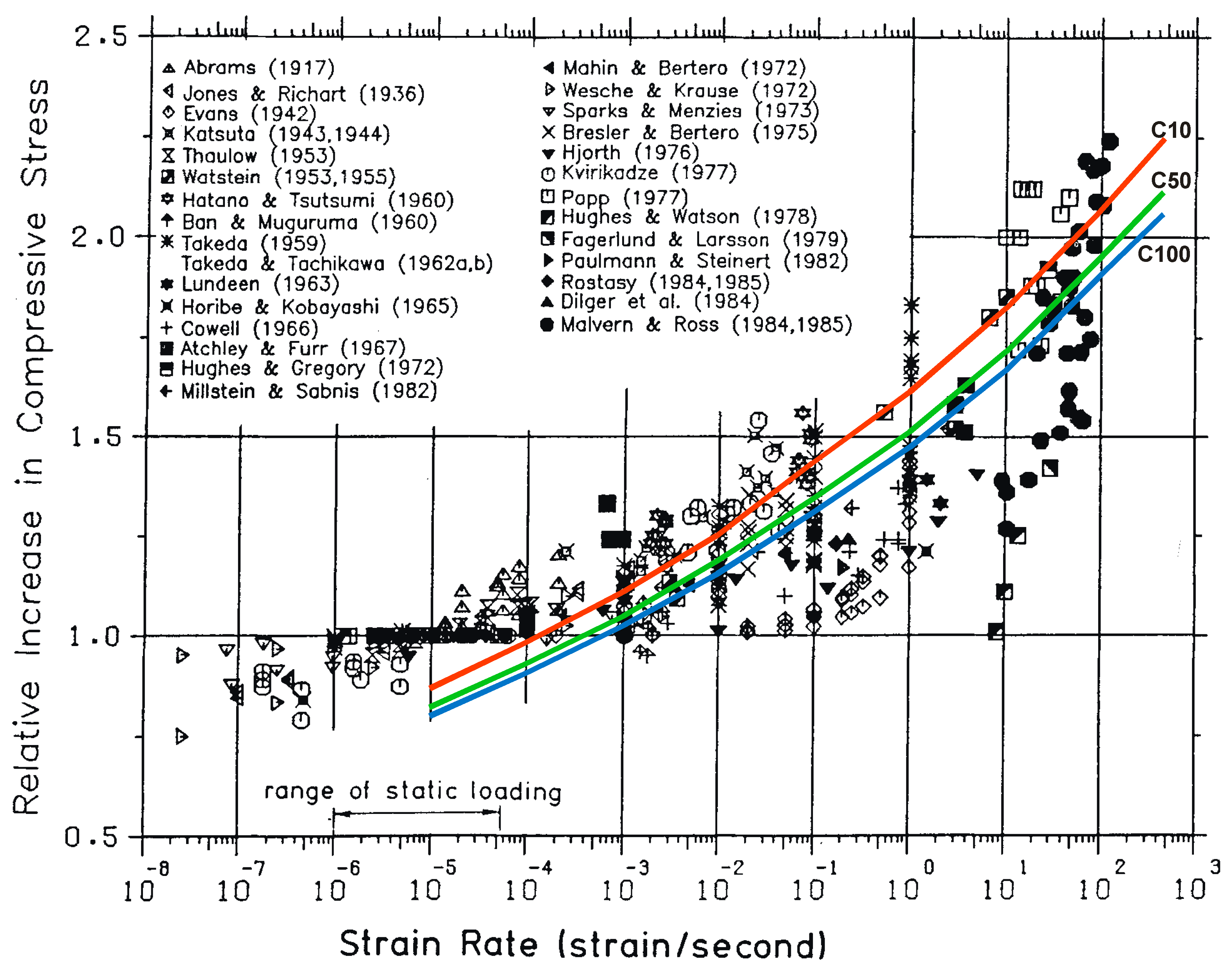
3.3. Comparisons for Dynamic Tests
4. Discussion
- Determination of the dynamic strength of concrete at any time-varying dynamic deformation process, using the universal integral criterion. This is—in the authors’ opinion—the main advantage of this model.
- Description of the spatial stress state, by means of a limit function, steered by the one parameter describing the homothetic expansion in the process of reaching the dynamic strength or shrinkage in the material softening process.
- Combination of two qualitatively different stages of the deformation process: (1) process of reaching the dynamic strength of concrete accumulated exclusively in the elastic range, and (2) quasi-static incremental elastic–plastic process at the level of determined dynamic strength.
- Estimation with the surplus of the elastic deformation range.
- Omission of the influence of strain rate on the increase of dynamic deformation modulus, which partially reduces the effect of the stiffness from increasing of material described in the previous point.
- Consideration of the degradation effect of the deformation modulus in the range of material softening.
- Description of cracking or crushing states of concrete as the stress-less states reached in the material softening processes at tension or compression.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kupfer, H.; Hilsdorf, H.K.; Rüsch, H. Behavior of concrete under biaxial stresses. J. Am. Concr. Inst. 1969, 66, 656–666. [Google Scholar]
- Mills, L.L.; Zimmerman, R.M. Compressive strength of plain concrete under multiaxial loading conditions. J. Am. Concr. Inst. 1970, 67, 802–807. [Google Scholar]
- Luanay, P.; Gachon, H. Strain and Ultimate Strength of Concrete Triaxial Stress; ACI Special Publish: Detriot, MI, USA, 1972; Volume 34. [Google Scholar]
- Schickert, G.; Winkler, H. Results of Test Concerning Strength and Strain of Concrete Subjected to Multiaxial Compressive Stresses; Deutscher Ausschüβfür Stahlbeton: Berlin, Germany, 1977; p. 277. [Google Scholar]
- Tasuji, E.; Slate, F.O.; Nilson, E.A. Stress-strain response and fracture of concrete in biaxial loading. J. Am. Concr. Inst. 1978, 75, 306–312. [Google Scholar]
- Nilsson, L. Impact Loading on Concrete Structures; Publication 79:1; Department of Structural Mechanics, Chalmers University of Technology: Göteborg, Sweden, 1979. [Google Scholar]
- Klisiński, M. Degradation and Plastic Deformation of Concrete; Institute of Fundamental Technological Research Polish Academy of Sciences: Warsaw, Poland, 1984; p. 38. (In Polish) [Google Scholar]
- Podgórski, J. Critical States in Solids with Internal Friction; Institute of Fundamental Technological Research Polish Academy of Sciences: Warsaw, Poland, 1986; p. 25. (In Polish) [Google Scholar]
- Hofstetter, G.; Mang, H.A. Computational Mechanics of Reinforced Concrete Structures Fundamentals and Advances in the Engineering Sciences; Vieweg: Braunschweig/Wiesbaden, Germany, 1995. [Google Scholar]
- Watstein, D. Effect of straining rate on the compressive strength and elastic properties of concrete. J. Am. Concr. Inst. 1953, 24, 729–744. [Google Scholar]
- Hansen, R.J.; Navy, E.G.; Shah, J.M. Response of concrete shear keys to dynamic loading. J. Am. Concr. Inst. 1961, 57, 1475–1490. [Google Scholar]
- Bazenov, J.M. Concrete under Dynamic Load; Izdatielstwo Litieratury po Stoitielstwu: Moscow, Russia, 1970. (In Russian) [Google Scholar]
- Zieliński, A.J. Fracture mechanism of concrete under tensile impact loads. Arch. Civ. Eng Wars. Pol. 1984, 30, 709–721. (In Polish) [Google Scholar]
- Rostasy, F.S.; Hartwich, K. Compressive strength and deformation of steel fibre reinforced concrete under high rate of strain. Int. J. Cem. Compos. Lightweight Concr. 1985, 7, 21–28. [Google Scholar] [CrossRef]
- Soroushian, P.; Choi, K.B.; Alhamad, A. Dynamic constitutive behavior of concrete. J. Am. Concr. Inst. 1986, 83, 251–259. [Google Scholar]
- Popov, G.I. Reinforced Concrete Structures under Impulsive Loads; Strojizdat: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Dilger, W.H.; Koch, R.; Kowalczyk, R. Ductility of plain and confined concrete under different strain rates. J. Am. Concr. Inst. 1984, 81, 73–81. [Google Scholar]
- Kowalczyk, R.; Dilger, W. Deformability of Concrete and Reinforced Concrete; Institute of Fundamental Technological Research Polish Academy of Sciences: Warsaw, Poland, 1971; p. 44. (In Polish) [Google Scholar]
- Karsan, I.D.; Jirsa, J.D. Behavior of concrete under compressive loadings. J. Struct. Div. 1969, 95, 2543–2563. [Google Scholar]
- Sinha, B.P.; Gerstle, K.H.; Tulin, L.G. Stress-strain relations for concrete under cyclic loading. J. Am. Concr. Inst. 1964, 61, 195–210. [Google Scholar]
- Nilson, A.H. Nonlinear analysis of reinforced concrete by the finite element method. J. Am. Concr. Inst. 1968, 65, 757–766. [Google Scholar]
- Bažant, Z.P.; Tsubaki, T. Total strain theory and path-dependence of concrete. J. Eng. Mech. Div. ASCE 1980, 106, 1151–1173. [Google Scholar]
- Kupfer, H.B.; Gerstle, K.H. Behavior of concrete under biaxial stresses. J. Eng. Mech. Div. ASCE 1973, 99, 853–867. [Google Scholar]
- Willam, K.J.; Warnke, E.P. Constitutive Model for the Triaxial Behavior of Concrete. In Proceedings of the International Association for Bridge and Structural Engineering, Seminar on Concrete Structures Subjected to Triaxial Stresses, Bergamo, Italy, 17–19 May 1974; Volume III-1, pp. 1–30. [Google Scholar]
- Bažant, Z.P.; Kim, S.S. Plastic-fracturing theory for concrete. J. Eng. Mech. Div. ASCE 1979, 105, 407–428. [Google Scholar]
- Dragon, A.; Mróz, Z. A continuum model for plastic-brittle behavior of rock and concrete. J. Eng. Sci. 1979, 17, 121–137. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Bhat, P. Endochronic theory of inelasticity and failure of concrete. J. Eng. Mech. Div. ASCE 1976, 102, 331–344. [Google Scholar]
- Kowalczyk, R.; Sawczuk, A. Modeling of Concrete Behavior under Dynamic Loadings. In Proceedings of the RILEM-CEB-IABSE-IAAS-Interassociation Symposium Concrete Structures under Impact and Impulsive Loading, Berlin (West), Germany, 2–4 June 1982; Volume II, pp. 92–100. [Google Scholar]
- Perzyna, P. The constitutive equations for rate sensitive plastic materials. Quart. Appl. Math. 1963, 20, 321–332. [Google Scholar] [CrossRef] [Green Version]
- Marzec, I.; Tejchman, J. Computational modelling of concrete behaviour under static and dynamic conditions. Bull. Pol. Acad. Sci. Tech. Sci. 2013, 61, 85–96. [Google Scholar] [CrossRef]
- Mazars, J.; Hamon, F.; Grange, S. A new 3D damage model for concrete under monotonic, cyclic and dynamic loadings. Mater. Struct. Constr. 2015, 48, 3779–3793. [Google Scholar] [CrossRef]
- Grassl, P.; Nystrom, U.; Rempling, R.; Gylltoft, K. A damage-plasticity model for the dynamic failure of concrete. In Proceedings of the 8th International Conference on Structural Dynamics, Leuven, Belgium, 4–6 July 2011. [Google Scholar]
- Wang, G.; Lu, D.; Du, X.; Zhou, X. Dynamic Multiaxial Strength Criterion for Concrete Based on Strain Rate–Dependent Strength Parameters. J. Eng. Mech. ASCE 2018, 144, 4018018. [Google Scholar] [CrossRef]
- Kong, X.; Fang, Q.; Chen, L.; Wu, H. A new material model for concrete subjected to intense dynamic loadings. Int. J. Impact Eng. 2018, 120, 60–78. [Google Scholar] [CrossRef]
- Forquin, P.; Erzar, B. Dynamic fragmentation process in concrete under impact and spalling tests. Int. J. Fract. 2010, 163, 193–215. [Google Scholar] [CrossRef]
- Ožbolt, J.; Sharma, A.; Reinhardt, H.W. Dynamic fracture of concrete—Compact tension specimen. Int. J. Solids Struct. 2011, 48, 1534–1543. [Google Scholar] [CrossRef]
- Snozzi, L.; Gatuingt, F.; Molinari, J.-F. A meso-mechanical model for concrete under dynamic tensile and compressive loading. Int. J. Fract. 2012, 178, 179–194. [Google Scholar] [CrossRef] [Green Version]
- Bąk, G.; Stolarski, A. Nonstandard idealization of dynamic behavior of concrete under uniaxial compression. Eng. Trans. Wars. Pol. 1988, 2, 217–238. (In Polish) [Google Scholar]
- Bąk, G.; Stolarski, A. Nonlinear Analysis of Reinforced Concrete Bar Structures Impulsively Loaded; Studies in the Range of Engineering; Polish Academy of Sciences Publishers: Warsaw, Poland, 1990; p. 30. (In Polish) [Google Scholar]
- Stolarski, A. Dynamic strength criterion for concrete. J. Eng. Mech. ASCE 2004, 130, 1428–1435. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A Plastic-Damage Model for Concrete. Int. J. Solids Struct. 1989, 25, 299–329. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. ASCE 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Il’Yushin, A.A. On the Postulate of Plasticity; Prikładnaja Matematika i Mekhanika: Moscow, Russia, 1961; Volume 25, pp. 503–507. (In Russian) [Google Scholar]
- Reimann, H. Kritische Spannunszustände des Betons Bei Mehrachsiger, Ruhender Kurzzeitbelastung; Deutscher Ausschüβ für Stahlbeton: Berlin, Germany, 1965; Volume 1, p. 75. (In German) [Google Scholar]
- Ottosen, N.S. A failure criterion for concrete. J. Eng. Mech. Div. ASCE 1977, 103, 527–535. [Google Scholar]
- Walther, R. Über Die Berechnung der Schubtragfähigkeit von Stahl—Und Spannbetonbalken; Beton und Stahlbeton: Berlin, Germany, 1962; Volume 11, pp. 261–271. (In German) [Google Scholar]
- Ohtani, Y.; Chen, W.F. A plastic-softening model for concrete materials. Comp. Struct. 1989, 33, 1047–1055. [Google Scholar] [CrossRef]
- Bischoff, P.H.; Perry, S.H. Compressive behaviour of concrete at high strain rates. Mater. Struct. 1991, 24, 425–450. [Google Scholar] [CrossRef]
- Yan, D.; Lin, G. Dynamic behaviour of concrete in biaxial compression. Mag. Concr. Res. 2007, 59, 45–52. [Google Scholar] [CrossRef]
- Guan, P.; Liu, P. Study of strength criterion for dynamic biaxial compressive properties of concrete under constant confining pressure. In Proceedings of the International Conference on Electric Technology and Civil Engineering, Lushan, China, 22–24 April 2011; IEEE: New York, NY, USA, 2011; pp. 753–755. [Google Scholar]
- Shang, S.M.; Song, Y.P. Dynamic biaxial tensile-compressive strength and failure criterion of plain concrete. Constr. Build. Mater. 2013, 40, 322–329. [Google Scholar]
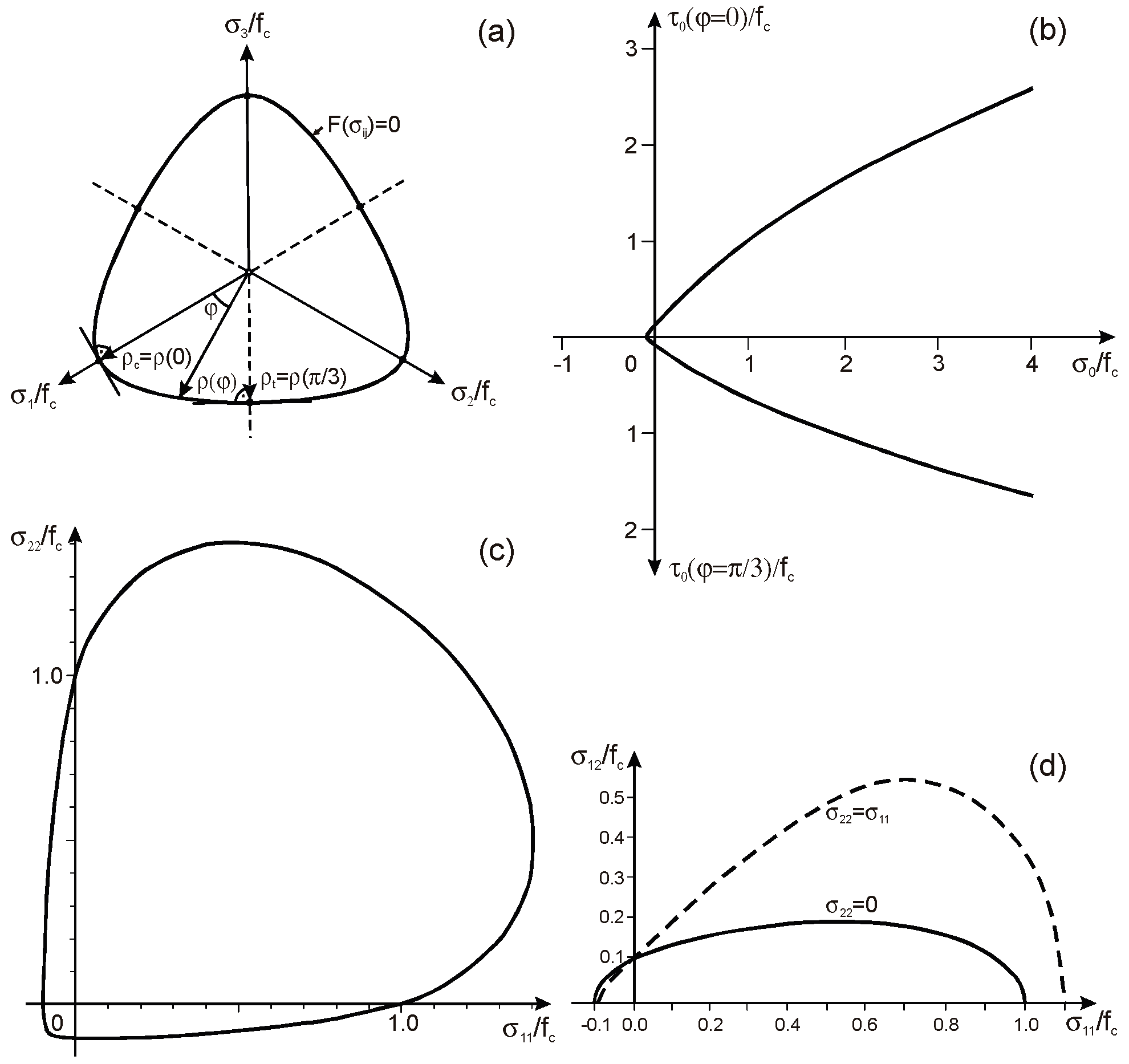





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stolarski, A.; Cichorski, W.; Szcześniak, A. Non-Classical Model of Dynamic Behavior of Concrete. Appl. Sci. 2019, 9, 2590. https://doi.org/10.3390/app9132590
Stolarski A, Cichorski W, Szcześniak A. Non-Classical Model of Dynamic Behavior of Concrete. Applied Sciences. 2019; 9(13):2590. https://doi.org/10.3390/app9132590
Chicago/Turabian StyleStolarski, Adam, Waldemar Cichorski, and Anna Szcześniak. 2019. "Non-Classical Model of Dynamic Behavior of Concrete" Applied Sciences 9, no. 13: 2590. https://doi.org/10.3390/app9132590
APA StyleStolarski, A., Cichorski, W., & Szcześniak, A. (2019). Non-Classical Model of Dynamic Behavior of Concrete. Applied Sciences, 9(13), 2590. https://doi.org/10.3390/app9132590




