Quantum Calibration of Photon-Number-Resolving Detectors Based on Multi-Pixel Photon Counters
Abstract
:1. Introduction
2. Materials and Methods
2.1. Multi-Pixel Photon Counter (MPPC)
2.2. Quantum Detector Tomography (QDT)
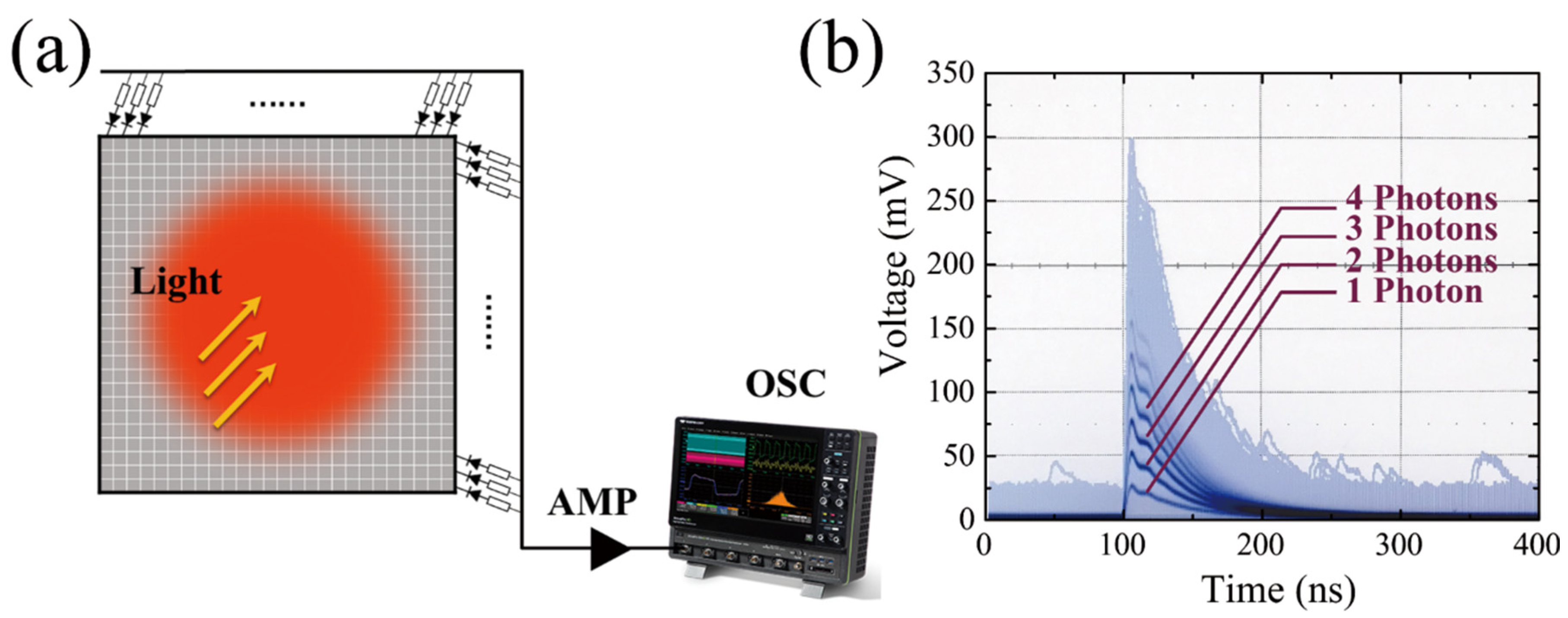
2.3. Experimental Setup
3. Results
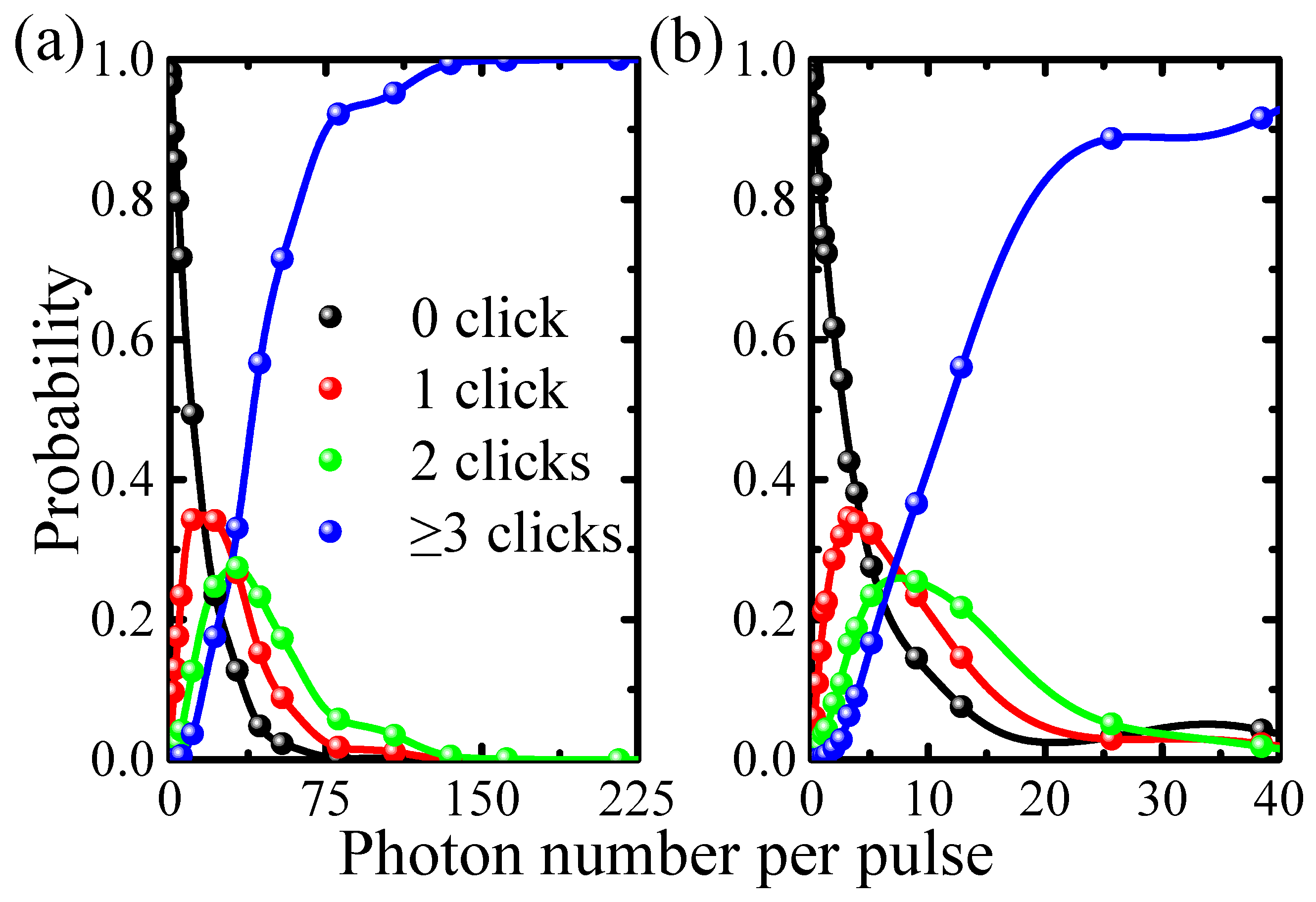
3.1. Photon Number Distribution Histogram
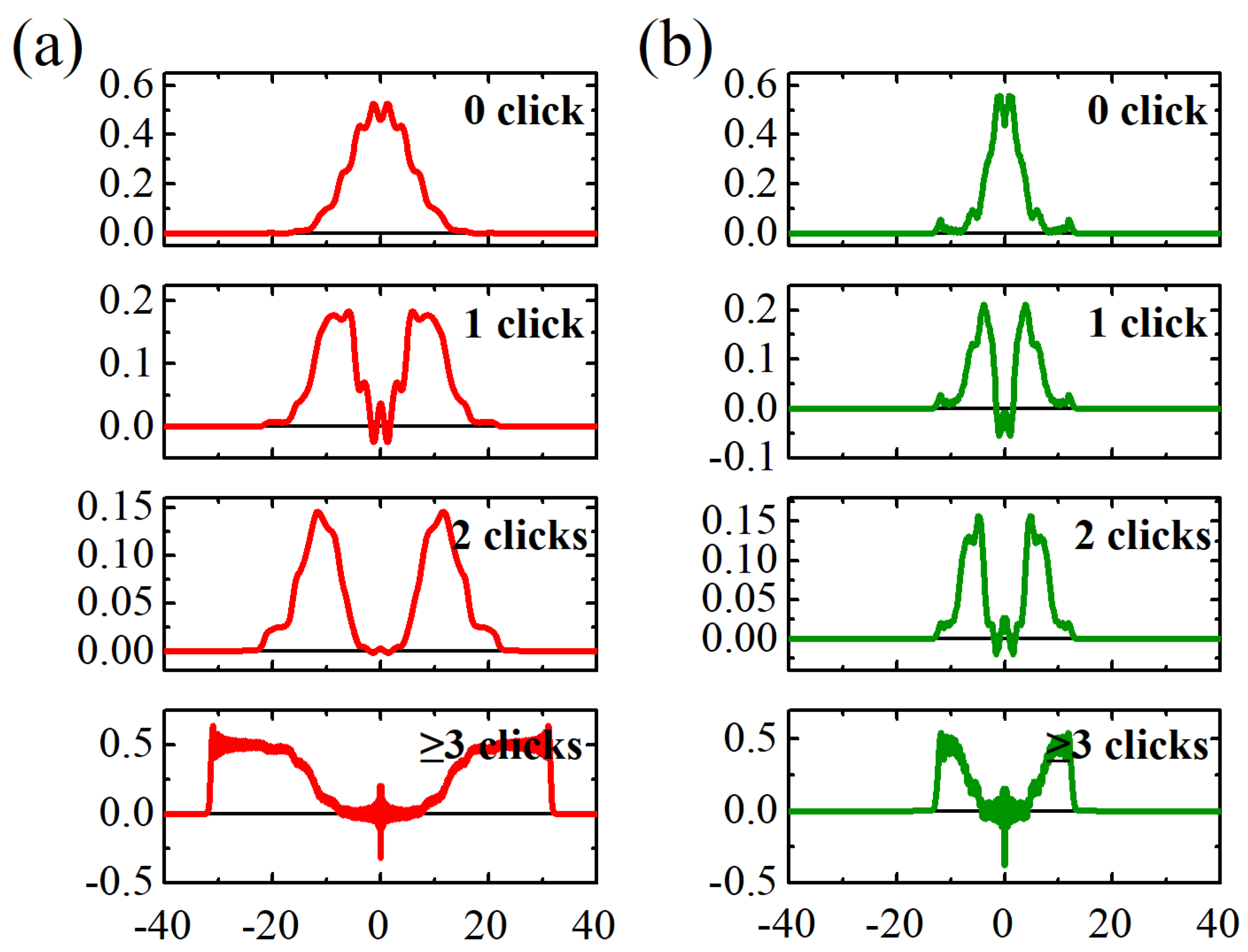
3.2. POVM
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kalashnikov, D.A.; Tan, S.H.; Krivitsky, L.A. Crosstalk calibration of multi-pixel photon counters using coherent states. Opt. Express 2012, 20, 5044–5051. [Google Scholar] [CrossRef] [PubMed]
- Allevi, A.; Bondani, M.; Andreoni, A. Photon-number correlations by photon-number resolving detectors. Opt. Lett. 2010, 35, 1707–1709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Waks, E.; Diamanti, E.; Sanders, B.C.; Bartlett, S.D.; Yamamoto, Y. Direct observation of nonclassical photon statistics in parametric down-conversion. Phys. Rev. Lett. 2004, 92, 113602/1-4. [Google Scholar] [CrossRef] [PubMed]
- Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef] [PubMed]
- Kato, G.; Tamaki, K. Security of six-state quantum key distribution protocol with threshold detectors. Sci. Rep. 2016, 6, 30044/1-5. [Google Scholar] [CrossRef] [PubMed]
- Jian, Y.; Wu, E.; Chen, X.; Wu, G.; Zeng, H. Time-dependent photon number discrimination of InGaAs/InP avalanche photodiode single-photon detector. Appl. Opt. 2011, 50, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Ren, M.; Wu, E.; Liang, Y.; Jian, Y.; Wu, G.A.; Zeng, H.P. Quantum random-number generator based on a photon-number-resolving detector. Phys. Rev. 2011, 83, 023820/1-4. [Google Scholar] [CrossRef]
- Gao, Y.; Anisimov, P.M.; Wildfeuer, C.F.; Luine, J.; Lee, H.; Dowling, J.P. Super-resolution at the shot-noise limit with coherent states and photon-number-resolving detectors. J. Opt. Soc. Am. 2010, 27, A170–A174. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Liu, D.; Zhang, W.; You, L.; He, Y.; Zhang, W.; Yang, X.; Wu, G.; Ren, M.; Zeng, H.; et al. Time-of-flight laser ranging and imaging at 1550 nm using low-jitter superconducting nanowire single-photon detection system. Appl. Opt. 2013, 52, 3241–3245. [Google Scholar] [CrossRef] [Green Version]
- McCarthy, A.; Krichel, N.J.; Gemmell, N.R.; Ren, X.; Tanner, M.G.; Dorenbos, S.N.; Zwiller, V.; Hadfield, R.H.; Buller, G.S. Kilometer-range, high resolution depth imaging via 1560 nm wavelength single-photon detection. Opt. Express 2013, 21, 8904–8915. [Google Scholar] [CrossRef] [Green Version]
- Bao, Z.; Liang, Y.; Wang, Z.; Li, Z.; Wu, E.; Wu, G.; Zeng, H. Laser ranging at few-photon level by photon-number-resolving detection. Appl. Opt. 2014, 53, 3908–3912. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Wang, Y.-Q.; Zhang, X.-F.; Wang, C.-Y. Subpixel three-dimensional laser imaging with a downscaled avalanche photodiode array using code division multiple access. Communications Physics 2019, 2, 1. [Google Scholar] [CrossRef]
- Miyamoto, H.; Teshima, M. SiPM development for the imaging Cherenkov and fluorescence telescopes. Nucl. Instrum. Methods Phys. Res. 2010, 623, 198–200. [Google Scholar] [CrossRef]
- Poland, S.P.; Krstajic, N.; Monypenny, J.; Coelho, S.; Tyndall, D.; Walker, R.J.; Devauges, V.; Richardson, J.; Dutton, N.; Barber, P.; et al. A high speed multifocal multiphoton fluorescence lifetime imaging microscope for live-cell FRET imaging. Biomed. Opt. Express. 2015, 6, 277–296. [Google Scholar] [CrossRef] [PubMed]
- Petralia, S.; Sciuto, E.L.; Santangelo, M.F.; Libertino, S.; Messina, M.A.; Conoci, S. Sulfide Species Optical Monitoring by a Miniaturized Silicon Photomultiplier. Sensors 2018, 18, 727. [Google Scholar] [CrossRef] [PubMed]
- Asrar, P.; Sucur, M.; Hashemi, N. Multi-Pixel Photon Counters for Optofluidic Characterization of Particles and Microalgae. Biosensors 2015, 5, 308–318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thompson, C.J.; Goertzen, A.L.; Thiessen, J.D.; Bishop, D.; Stortz, G.; Kozlowski, P.; Retiere, F.; Zhang, X.; Sossi, V. Development of a PET scanner for simultaneously imaging small animals with MRI and PET. Sensors 2014, 14, 14654–14671. [Google Scholar] [CrossRef] [PubMed]
- D’Ascenzo, N.; Gao, M.; Antonecchia, E.; Gnudi, P.; Chen, H.H.; Chen, F.H.; Hong, J.H.; Hsiao, I.T.; Yen, T.C.; Wang, W.; et al. New Digital Plug and Imaging Sensor for a Proton Therapy Monitoring System Based on Positron Emission Tomography. Sensors 2018, 18, 3006. [Google Scholar] [CrossRef]
- Gola, A.; Acerbi, F.; Capasso, M.; Marcante, M.; Mazzi, A.; Paternoster, G.; Piemonte, C.; Regazzoni, V.; Zorzi, N. NUV-Sensitive Silicon Photomultiplier Technologies Developed at Fondazione Bruno Kessler. Sensors 2019, 19, 308. [Google Scholar] [CrossRef]
- Chao, K.L.; Dhakal, S.; Qin, J.W.; Kim, M.; Peng, Y.K. A 1064 nm Dispersive Raman Spectral Imaging System for Food Safety and Quality Evaluation. Appl. Sci. 2018, 8, 431. [Google Scholar] [CrossRef]
- Smith, D.H.; Gillett, G.; de Almeida, M.P.; Branciard, C.; Fedrizzi, A.; Weinhold, T.J.; Lita, A.; Calkins, B.; Gerrits, T.; Wiseman, H.M.; et al. Conclusive quantum steering with superconducting transition-edge sensors. Nat. Commun. 2012, 3, 625. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fukuda, D.; Fujii, G.; Numata, T.; Amemiya, K.; Yoshizawa, A.; Tsuchida, H.; Fujino, H.; Ishii, H.; Itatani, T.; Inoue, S.; et al. Titanium-based transition-edge photon number resolving detector with 98% detection efficiency with index-matched small-gap fiber coupling. Opt. Express 2011, 19, 870–875. [Google Scholar] [CrossRef] [PubMed]
- Gerrits, T.; Calkins, B.; Tomlin, N.; Lita, A.E.; Migdall, A.; Mirin, R.; Nam, S.W. Extending single-photon optimized superconducting transition edge sensors beyond the single-photon counting regime. Opt. Express 2012, 20, 23798–23810. [Google Scholar] [CrossRef] [PubMed]
- Sridhar, N.; Shahrokhshahi, R.; Miller, A.J.; Calkins, B.; Gerrits, T.; Lita, A.; Nam, S.W.; Pfister, O. Direct measurement of the Wigner function by photon-number-resolving detection. J. Opt. Soc. Am. B 2014, 31, B34–B40. [Google Scholar] [CrossRef] [Green Version]
- Bub, G.; Tecza, M.; Helmes, M.; Lee, P.; Kohl, P. Temporal pixel multiplexing for simultaneous high-speed, high-resolution imaging. Nat Methods 2010, 7, 209–211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harder, G.; Silberhorn, C.; Rehacek, J.; Hradil, Z.; Motka, L.; Stoklasa, B.; Sanchez-Soto, L.L. Time-multiplexed measurements of nonclassical light at telecom wavelengths. Phys. Rev. A 2014, 90, 042105/1-6. [Google Scholar] [CrossRef]
- Kalashnikov, D.A.; Tan, S.H.; Chekhova, M.V.; Krivitsky, L.A. Accessing photon bunching with a photon number resolving multi-pixel detector. Opt. Express 2011, 19, 9352–9363. [Google Scholar] [CrossRef] [PubMed]
- Chrapkiewicz, R.; Wasilewski, W.; Banaszek, K. High-fidelity spatially resolved multiphoton counting for quantum imaging applications. Opt. Lett. 2014, 39, 5090–5093. [Google Scholar] [CrossRef]
- Mattioli, F.; Zhou, Z.; Gaggero, A.; Gaudio, R.; Leoni, R.; Fiore, A. Photon-counting and analog operation of a 24-pixel photon number resolving detector based on superconducting nanowires. Opt. Express 2016, 24, 9067–9076. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Ren, M.; Wu, E.; Wang, J.T.; Wu, G.; Zeng, H.P. High-Speed Photon-Number Resolving With Sinusoidally Gated Multipixel Photon Counters. IEEE PHOTONIC. TECH. L. 2012, 24, 1852–1855. [Google Scholar] [CrossRef]
- Nassalski, A.; Moszynski, M.; Syntfeld-Kazuch, A.; Szczesniak, T.; Swiderski, L.; Wolski, D.; Batsch, T.; Baszak, J. Multi Pixel Photon Counters (MPPC) as an Alternative to APD in PET Applications. IEEE Trans. Nucl. Sci. 2010, 57, 1008–1014. [Google Scholar] [CrossRef]
- Acerbi, F.; Paternoster, G.; Capasso, M.; Marcante, M.; Mazzi, A.; Regazzoni, V.; Zorzi, N.; Gola, A. Silicon Photomultipliers: Technology Optimizations for Ultraviolet, Visible and Near-Infrared Range. Instruments 2019, 3, 15. [Google Scholar] [CrossRef]
- Huang, K.; Gu, X.; Ren, M.; Jian, Y.; Pan, H.; Wu, G.; Wu, E.; Zeng, H. Photon-number-resolving detection at 1.04 mum via coincidence frequency upconversion. Opt. Lett. 2011, 36, 1722–1724. [Google Scholar] [CrossRef] [PubMed]
- Pomarico, E.; Sanguinetti, B.; Thew, R.; Zbinden, H. Room temperature photon number resolving detector for infared wavelengths. Opt. Express 2010, 18, 10750–10759. [Google Scholar] [CrossRef] [PubMed]
- Lundeen, J.S.; Feito, A.; Coldenstrodt-Ronge, H.; Pregnell, K.L.; Silberhorn, C.; Ralph, T.C.; Eisert, J.; Plenio, M.B.; Walmsley, I.A. Tomography of quantum detectors. Nature Physics 2009, 5, 27–30. [Google Scholar] [CrossRef]
- Afek, I.; Natan, A.; Ambar, O.; Silberberg, Y. Quantum state measurements using multipixel photon detectors. Phys. Rev. A 2009, 79, 043830. [Google Scholar] [CrossRef] [Green Version]
- Natarajan, C.M.; Zhang, L.; Coldenstrodt-Ronge, H.; Donati, G.; Dorenbos, S.N.; Zwiller, V.; Walmsley, I.A.; Hadfield, R.H. Quantum detector tomography of a time-multiplexed superconducting nanowire single-photon detector at telecom wavelengths. Opt. Express 2013, 21, 893–902. [Google Scholar] [CrossRef]
- Chesi, G.; Malinverno, L.; Allevi, A.; Santoro, R.; Caccia, M.; Martemiyanov, A.; Bondani, M. Optimizing Silicon photomultipliers for Quantum Optics. Sci. Rep. 2019, 9, 7433. [Google Scholar] [CrossRef]
- Fiurasek, J. Maximum-likelihood estimation of quantum measurement. Phys. Rev. A 2001, 64, 024102. [Google Scholar] [CrossRef] [Green Version]
- Ramilli, M.; Allevi, A.; Chmill, V.; Bondani, M.; Caccia, M.; Andreoni, A. Photon-number statistics with silicon photomultipliers. J. Opt. Soc. Am. B 2010, 27, 852. [Google Scholar] [CrossRef]
- Chen, X.; Ding, C.; Pan, H.; Huang, K.; Laurat, J.; Wu, G.; Wu, E. Temporal and spatial multiplexed infrared single-photon counter based on high-speed avalanche photodiode. Sci. Rep. 2017, 7, 44600. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feito, A.; Lundeen, J.S.; Coldenstrodt-Ronge, H.; Eisert, J.; Plenio, M.B.; Walmsley, I.A. Measuring measurement: theory and practice. New J. Phys. 2009, 11, 093038/1-39. [Google Scholar] [CrossRef]
- Sridhar, N.; Shahrokhshahi, R.; Miller, A.J.; Calkins, B.; Gerrits, T.; Lita, A.; Nam, S.W.; Pfister, O. Direct measurement of the Wigner function by photon-number-resolving detection. JOSA B 2014, 31, B34–B40. [Google Scholar] [CrossRef] [Green Version]
- D’Auria, V.; Lee, N.; Amri, T.; Fabre, C.; Laurat, J. Quantum decoherence of single-photon counters. Phys. Rev. Lett. 2011, 107, 050504. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Chen, Y.; Chen, X.; Ma, J.; Xu, G.; Wu, Y.; Xu, A.; Wu, E. Quantum Calibration of Photon-Number-Resolving Detectors Based on Multi-Pixel Photon Counters. Appl. Sci. 2019, 9, 2638. https://doi.org/10.3390/app9132638
Cai Y, Chen Y, Chen X, Ma J, Xu G, Wu Y, Xu A, Wu E. Quantum Calibration of Photon-Number-Resolving Detectors Based on Multi-Pixel Photon Counters. Applied Sciences. 2019; 9(13):2638. https://doi.org/10.3390/app9132638
Chicago/Turabian StyleCai, Yujie, Yu Chen, Xiuliang Chen, Jianhui Ma, Guangjian Xu, Yujing Wu, Aini Xu, and E Wu. 2019. "Quantum Calibration of Photon-Number-Resolving Detectors Based on Multi-Pixel Photon Counters" Applied Sciences 9, no. 13: 2638. https://doi.org/10.3390/app9132638
APA StyleCai, Y., Chen, Y., Chen, X., Ma, J., Xu, G., Wu, Y., Xu, A., & Wu, E. (2019). Quantum Calibration of Photon-Number-Resolving Detectors Based on Multi-Pixel Photon Counters. Applied Sciences, 9(13), 2638. https://doi.org/10.3390/app9132638





