Coherent Perfect Absorption Laser Points in One-Dimensional Anti-Parity–Time-Symmetric Photonic Crystals
Abstract
:1. Introduction
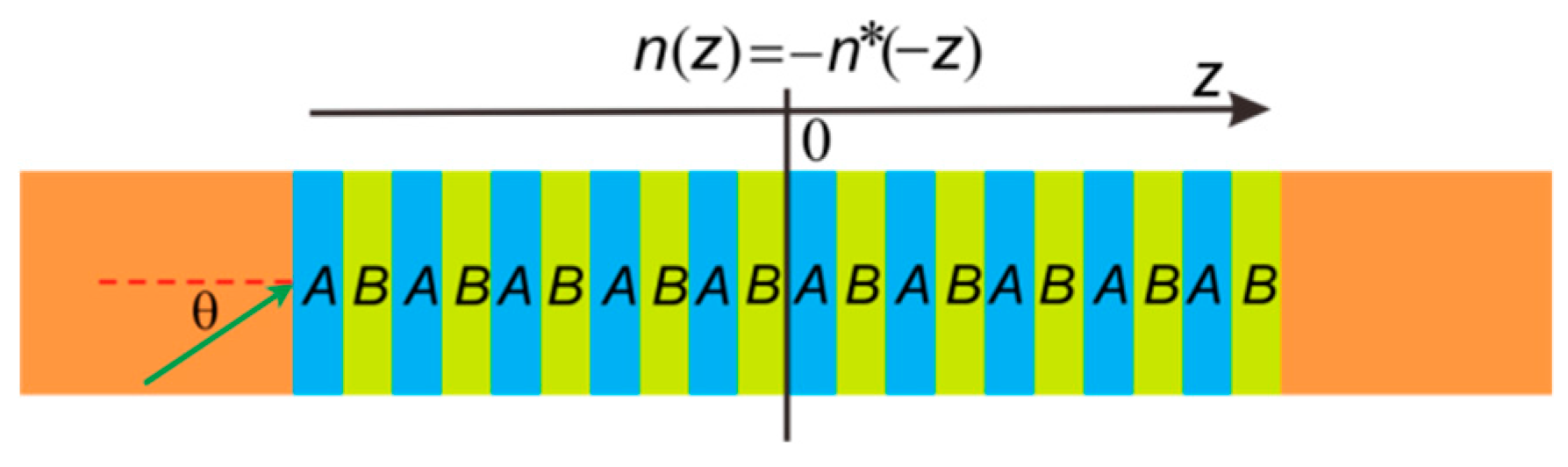
2. One-Dimensional Anti-PT-Symmetric PCs
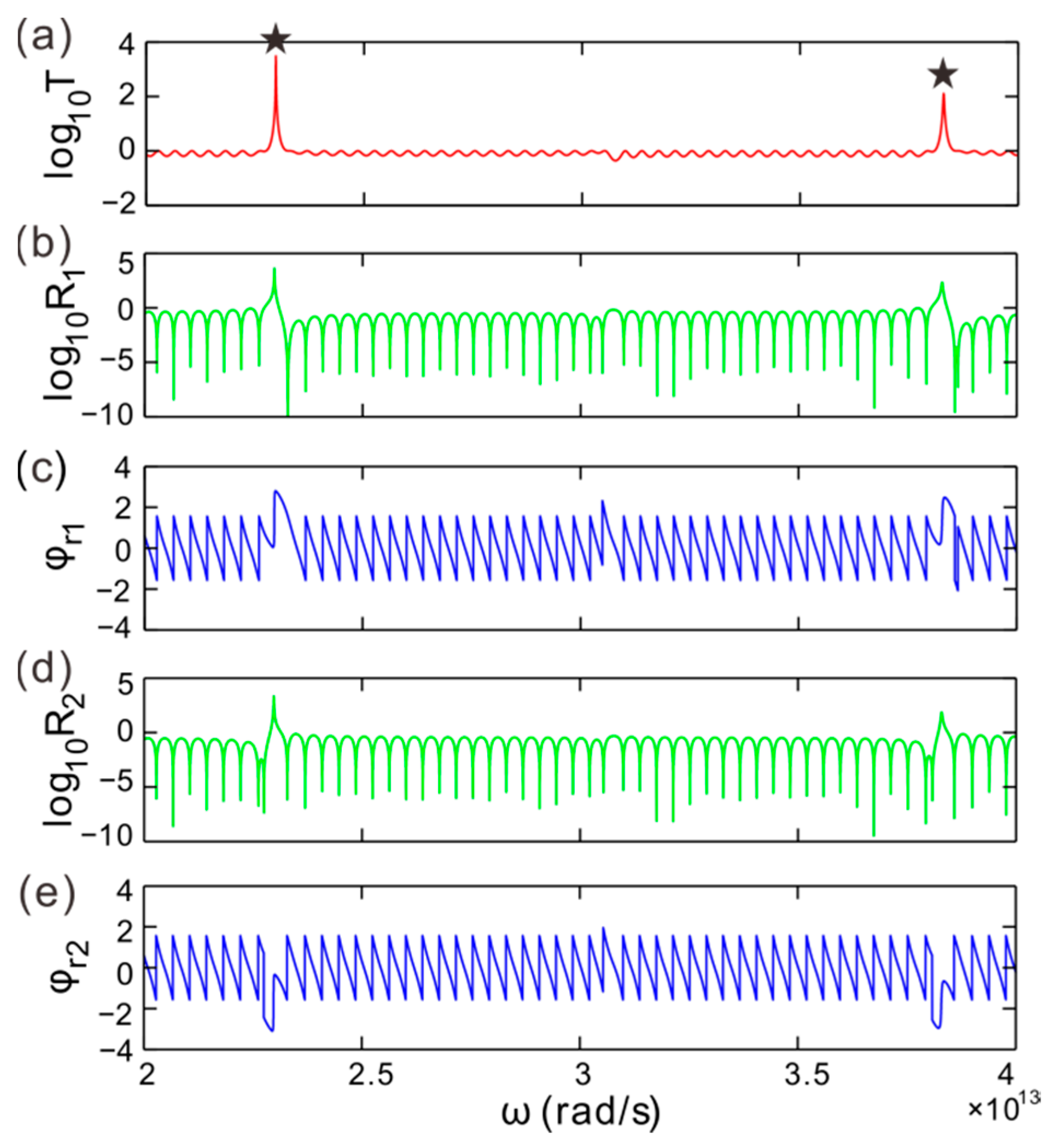
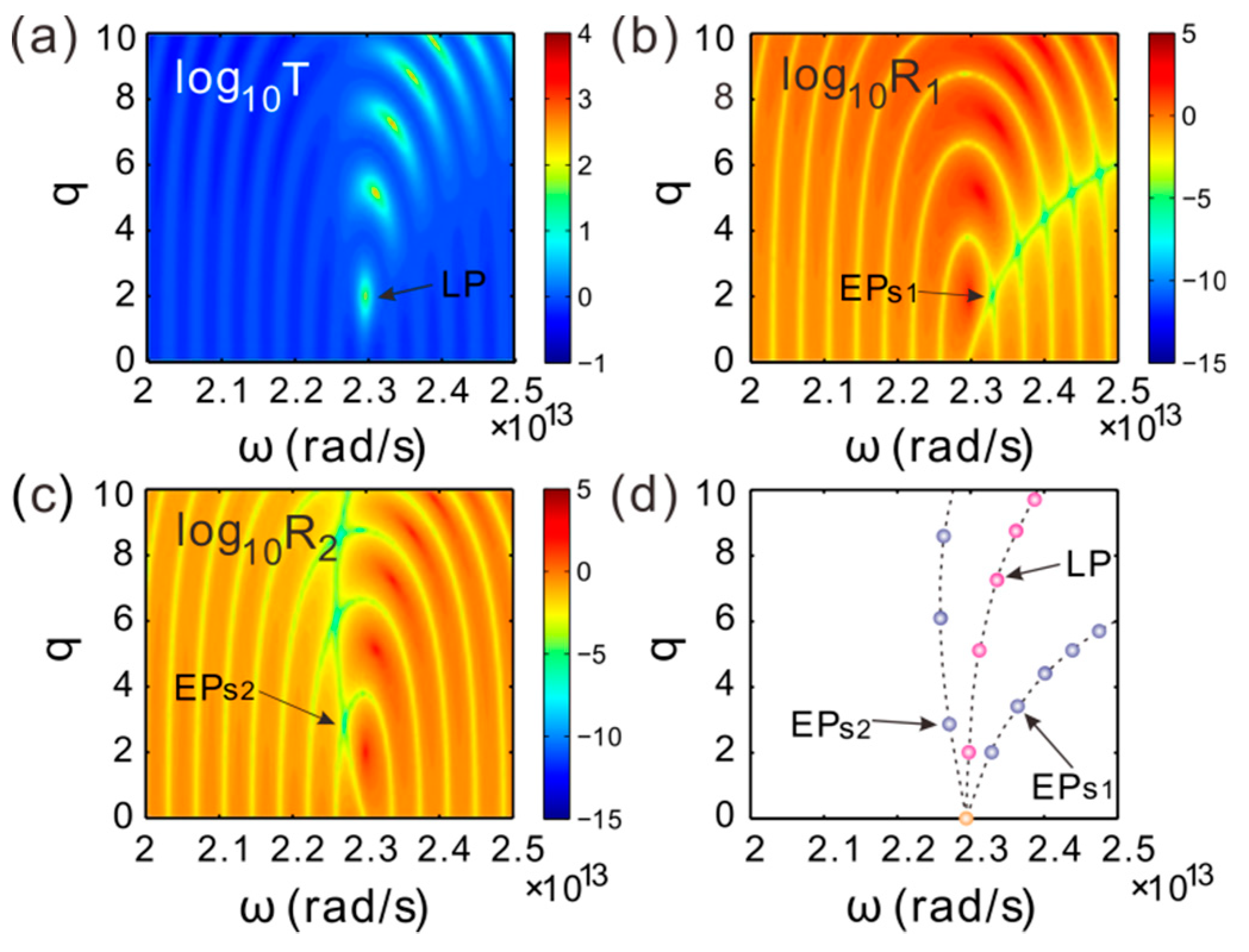
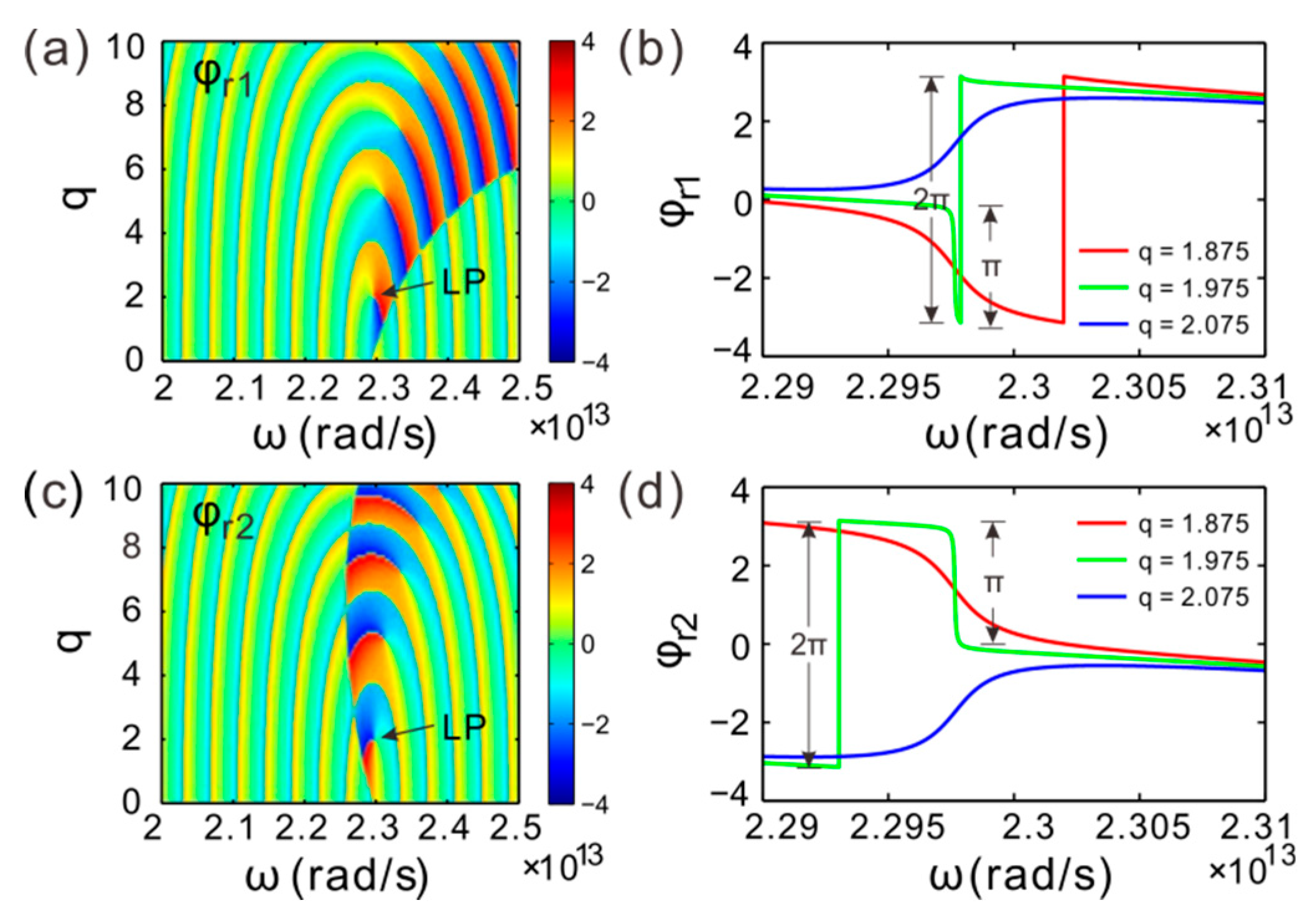
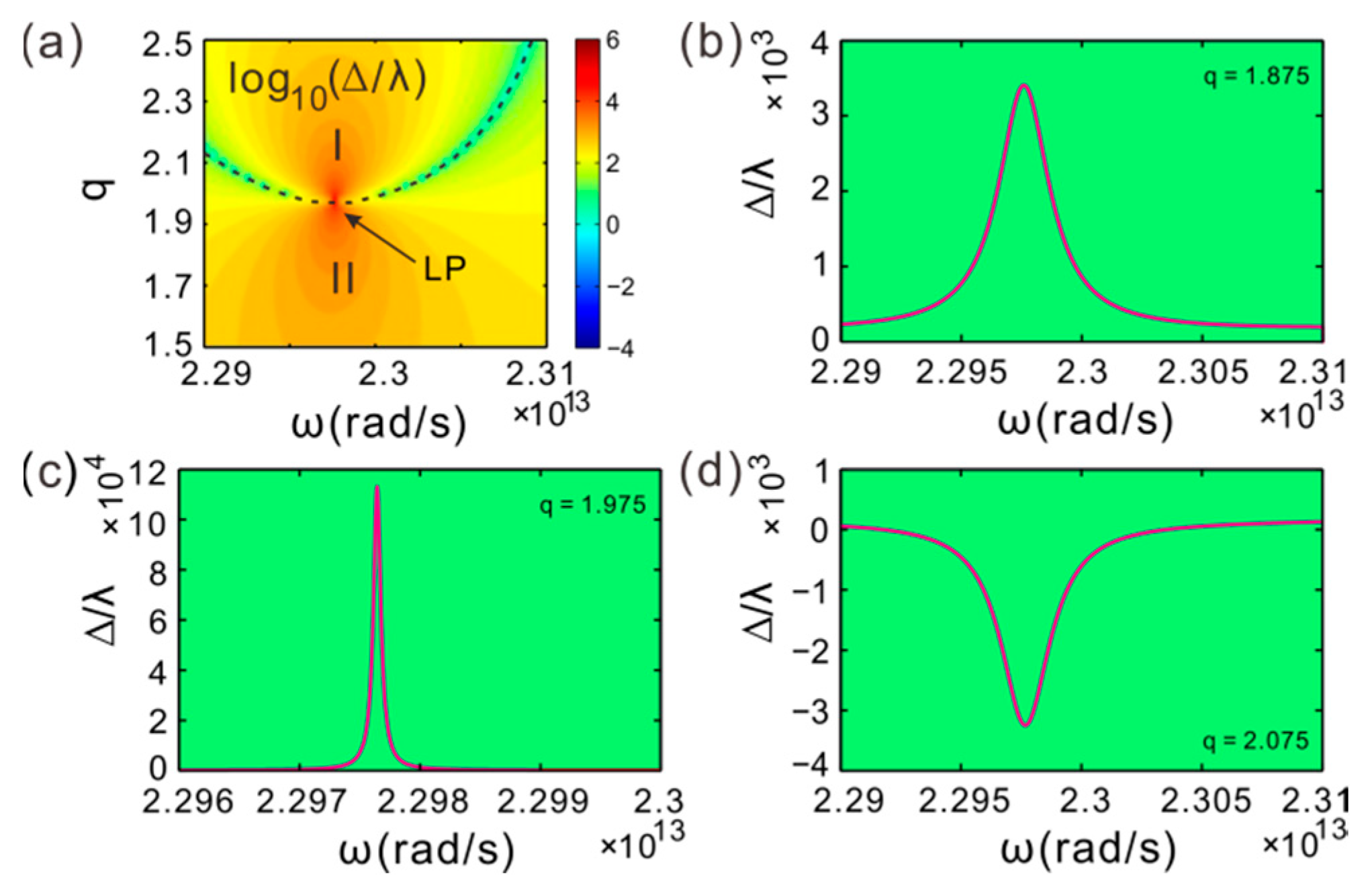
3. CPA-LPs and EPs Splitting
4. Large Spatial GH Shift Around CPA-LPs
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Joannopoulos, J.D.; Villeneuve, P.R.; Fan, S. Photonic crystals: Putting a new twist on light. Nature 1997, 386, 143. [Google Scholar] [CrossRef]
- Zhao, D.; Ke, S.; Hu, Y.; Wang, B.; Lu, P. Optical bistability in parity-time-symmetric dielectric multilayers incorporated with graphene. J. Opt. Soc. Am. B 2019, 36, 1731–1737. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, F.; Meng, P.; Wen, J.; Xu, S.; Li, Z.; Zhong, D. Reflection enhancement and giant lateral shift in defective photonic crystals with graphene. Appl. Sci. 2019, 9, 2141. [Google Scholar] [CrossRef]
- Yablonovitch, E. Photonic crystals: Semiconductors of light. Sci. Am. 2001, 285, 46–55. [Google Scholar] [CrossRef]
- Soukoulis, C.M. Photonic Crystals and Light Localization in the 21st Century; Springer Science and Business Media: Dordrecht, The Netherlands, 2012; Volume 563. [Google Scholar]
- Mingaleev, S.F.; Kivshar, Y.S. Nonlinear transmission and light localization in photonic-crystal waveguides. J. Opt. Soc. Am. B 2002, 19, 2241–2249. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Wang, Z.Q.; Long, H.; Wang, K.; Wang, B.; Lu, P.X. Optical bistability in defective photonic multilayers doped by graphene. Opt. Quant. Electron. 2017, 49, 163. [Google Scholar] [CrossRef]
- Zhao, D.; Zhong, D.; Hu, Y.; Ke, S.; Liu, W. Imaginary modulation inducing giant spatial Goos-Hänchen shifts in one-dimensional defective photonic lattices. Opt. Quant. Electron. 2019, 51, 113. [Google Scholar] [CrossRef]
- Cakmak, A.O.; Colak, E.; Serebryannikov, A.E.; Ozbay, E. Unidirectional transmission in photonic-crystal gratings at beam-type illumination. Opt. Express 2010, 18, 22283–22298. [Google Scholar] [CrossRef] [Green Version]
- Khanikaev, A.B.; Steel, M.J. Low-symmetry magnetic photonic crystals for nonreciprocal and unidirectional devices. Opt. Express 2009, 17, 5265–5272. [Google Scholar] [CrossRef]
- Vasić, B.; Gajić, R. Self-focusing media using graded photonic crystals: Focusing, Fourier transforming and imaging, directive emission, and directional cloaking. J. Appl. Phys. 2011, 110, 053103. [Google Scholar] [CrossRef]
- Xu, S.L.; Xue, L.; Belić, M.R.; He, J.R. Spatiotemporal soliton clusters in strongly nonlocal media with variable potential coefficients. Nonlinear Dyn. 2017, 87, 827–834. [Google Scholar] [CrossRef]
- Xu, S.L.; Petrovi, N.; Belić, M.R.; Deng, W. Exact solutions for the quintic nonlinear Schrödinger equation with time and space. Nonlinear Dyn. 2017, 84, 251–259. [Google Scholar] [CrossRef]
- Xu, S.L.; Petrović, N.; Belić, M.R. Exact solutions of the (2+1)-dimensional quintic nonlinear Schrödinger equation with variable coefficients. Nonlinear Dyn. 2015, 80, 583–589. [Google Scholar] [CrossRef]
- Meng, P.; Zhao, D.; Zhong, D.; Liu, W. Topological plasmonic modes in graphene-coated nanowire arrays. Opt. Quant. Electron. 2019, 51, 156. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, B.; Long, H.; Wang, K.; Lu, P. Surface plasmonic lattice solitons in semi-infinite graphene sheet arrays. J. Lightwave Technol. 2017, 35, 2960–2965. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, Q.; Wu, S.; Wang, B.; Lu, P. Optical imaginary directional couplers. J. Lightwave Technol. 2018, 36, 2510–2515. [Google Scholar] [CrossRef]
- Li, Z.P.; Xu, Z.M.; Qu, X.P.; Wang, S.B.; Peng, J.; Mei, L.H. Fabrication of nanopore and nanoparticle arrays with high aspect ratio AAO masks. Nanotechnology 2017, 28, 095301. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Guo, Q.; Xu, S.; Belic, M.R.; Zhao, Y.; Zhao, D.; He, J. Vortex Solitons in Bose-Einstein Condensates with Spin-Orbit Coupling and Gaussian Optical Lattices. Appl. Math. Lett. 2019, 92, 15–21. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, S.; Xie, M.; Zeng, H. GeSe monolayer semiconductor with tunable direct band gap and small carrier. Appl. Phys. Lett. 2015, 107, 122107. [Google Scholar] [CrossRef]
- Ni, H.; Li, M.; Hu, Y.; Mao, C.; Xue, L.; Zeng, H.; Yan, Z.; Wu, Y.; Zheng, C. Two-dimensional SnSe/GeSe van der Waals heterostructure with strain-tunable electronic and optical properties. J. Phys. Chem. Solids 2019, 131, 223–229. [Google Scholar] [CrossRef]
- Kinyua, D.M.; Long, H.; Xing, X.; Njoroge, S.; Wang, K.; Wang, B.; Lu, P. Gigahertz acoustic vibrations of Ga-doped ZnO nanoparticle array. Nanotechnology 2019, 30, 305201. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Xu, Z.; Qu, X.; Wang, S.; Peng, J. Pattern transfer of hexagonal packed structure via ultrathin metal nanomesh masks for formation of Si nanopore arrays. J. Alloys Compd. 2017, 695, 458–461. [Google Scholar] [CrossRef]
- Li, Z.; Wang, G.; Li, Z.; Cheng, Z.; Zhou, G.; Li, S. Flexible transparent electrodes based on gold nanomeshes. Nanoscale Res. Lett. 2019, 14, 132. [Google Scholar] [CrossRef] [PubMed]
- Longhi, S. Quantum-optical analogies using photonic structures. Laser Photon. Rev. 2009, 3, 243–261. [Google Scholar] [CrossRef]
- Zhen, B.; Hsu, C.W.; Igarashi, Y.; Lu, L.; Kaminer, I.; Pick, A.; Chua, S.; Joannopoulos, J.D.; Soljačić, M. Spawning rings of exceptional points out of Dirac cones. Nature 2015, 525, 354–358. [Google Scholar] [CrossRef]
- Feng, L.; Zhu, X.; Yang, S.; Zhu, H.; Zhang, P.; Yin, X.; Wang, Y.; Zhang, X. Demonstration of a large-scale optical exceptional point structure. Opt. Express 2014, 22, 1760–1767. [Google Scholar] [CrossRef]
- Peng, B.; Ozdemir, S.K.; Rotter, S.; Yilmaz, H.; Liertzer, M.; Monifi, F.; Bender, C.M.; Nori, F.; Yang, L. Loss-induced suppression and revival of lasing. Science 2014, 346, 328–332. [Google Scholar] [CrossRef] [Green Version]
- Guo, A.; Salamo, G.J.; Duchesne, D.; Morandotti, R.; Christodoulides, D.N. Observation of PT-symmetry breaking in complex optical potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef]
- Zhu, X.F. Defect states and exceptional point splitting in the band gaps of one-dimensional parity-time lattices. Opt. Express 2015, 23, 22274–22284. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Hatano, N.; Nelson, D.R. Localization transitions in non-Hermitian quantum mechanics. Phys. Rev. Lett. 1996, 77, 570–573. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.C.; Hsieh, M.H.; Flammia, S.T.; Lee, R.K. Local PT symmetry violates the no-signaling principle. Phys. Rev. Lett. 2014, 112, 130404. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.X.; Xu, S.L.; Belić, M.R.; Li, H.; Zhao, Y.; Deng, W.W.; Sun, Y.Z. Multipole solitons in a cold atomic gas with a parity-time symmetric potential. Nonlinear Dyn. 2019, 95, 2325–2332. [Google Scholar] [CrossRef]
- Bender, C.M. PT symmetry in quantum physics: From a mathematical curiosity to optical experiments. Europhysics News 2016, 47, 17–20. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, W.W.; Ke, S.L.; Liu, Q.J. Large lateral shift in complex dielectric multilayers with nearly parity–time symmetry. Opt. Quant. Electron. 2018, 50, 323. [Google Scholar] [CrossRef]
- Ke, S.; Liu, Q.; Zhao, D.; Liu, W. Spectral discrete diffraction with non-Hermitian coupling. J. Opt. Soc. Am. B 2018, 35, 2387–2393. [Google Scholar] [CrossRef]
- Ke, S.; Liu, J.; Liu, Q.; Zhao, D.; Liu, W. Strong absorption near exceptional points in plasmonic wave guide arrays. Opt. Quant. Electron. 2018, 50, 318. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, Q.; Liu, W. Adiabatic transfer of surface plasmons in non-Hermitian graphene waveguides. Opt. Quant. Electron. 2018, 50, 393. [Google Scholar] [CrossRef]
- Xu, S.L.; Zhao, Y.; Petrović, N.Z.; Belić, M.R. Spatiotemporal soliton supported by parity-time symmetric potential with competing nonlinearities. EPL 2016, 115, 14006. [Google Scholar] [CrossRef]
- Xu, S.L.; Petrović, N.; Belić, M.R.; Hu, Z.L. Light bullet supported by parity-time symmetric potential with power-law nonlinearity. Nonlinear Dyn. 2016, 84, 1877–1882. [Google Scholar] [CrossRef]
- Longhi, S. Parity-time symmetry meets photonics: A new twist in non-Hermitian optics. EPL 2018, 120, 64001. [Google Scholar] [CrossRef]
- Ruschhaupt, A.; Delgado, F.; Muga, J.G. Physical realization of PT-symmetric potential scattering in a planar slab waveguide. J. Phys. Math. Gen. 2005, 38, L171–L176. [Google Scholar] [CrossRef]
- Ruschhaupt, A.; Dowdall, T.; Simón, M.A.; Muga, J.G. Asymmetric scattering by non-Hermitian potentials. EPL 2018, 120, 20001. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity–time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Feng, L.; Xu, Y.L.; Fegadolli, W.S.; Lu, M.; Oliveira, J.E.B.; Almeida, V.R.; Chen, Y.; Scherer, A. Experimental demonstration of a unidirectional refectionless parity-time metamaterial at optical frequencies. Nat. Mater. 2013, 12, 108–113. [Google Scholar] [CrossRef] [PubMed]
- Regensburger, A.; Bersch, C.; Miri, M.A.; Onishchukov, G.; Christodoulides, D.N.; Peschel, U. Parity-time synthetic photonic lattices. Nature 2012, 488, 167–171. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; El-Ganainy, R.; Ge, L. Non-Hermitian photonics based on parity–time symmetry. Nat. Photon. 2017, 11, 752–762. [Google Scholar] [CrossRef]
- Ge, L.; Türeci, H.E. Antisymmetric PT-photonic structures with balanced positive- and negative-index materials. Phys. Rev. A 2013, 88, 053810. [Google Scholar] [CrossRef]
- Yang, F.; Liu, Y.; You, L. Anti-PT symmetry in dissipatively coupled optical systems. Phys. Rev. A 2017, 96, 053845. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, J.; Liu, Q.; Liao, Q.; Wang, B.; Lu, P. Topological bound modes in anti-PT-symmetric optical waveguide arrays. Opt. Express 2019, 27, 13858. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, T.; Sun, H.; Chan, C.T. Dynamically encircling an exceptional point in anti-PT-symmetric systems: asymmetric mode switching for symmetry-broken states. arXiv 2018, arXiv:1806.07649. [Google Scholar]
- Malzard, S.; Poli, C.; Schomerus, H. Topologically protected defect states in open photonic systems with non-Hermitian charge-conjugation and Parity-Time symmetry. Phys. Rev. Lett. 2015, 115, 200402. [Google Scholar] [CrossRef] [PubMed]
- Ge, L. Symmetry-protected zero-mode laser with a tunable spatial profile. Phys. Rev. A 2017, 95, 023812. [Google Scholar] [CrossRef] [Green Version]
- Kunst, F.K.; Edvardsson, E.; Budich, J.C.; Bergholtz, E.J. Biorthogonal bulk-boundary correspondence in non-Hermitian systems. Phys. Rev. Lett. 2018, 121, 026808. [Google Scholar] [CrossRef] [PubMed]
- Poli, C.; Bellec, M.; Kuhl, U.; Mortessagne, F.; Schomerus, H. Selective enhancement of topologically induced interface states in a dielectric resonator chain. Nat. Commun. 2015, 6, 6710. [Google Scholar] [CrossRef] [PubMed]
- Parto, M.; Wittek, S.; Hodaei, H.; Harari, G.; Bandres, M.A.; Ren, J.; Rechtsman, M.C.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Edge-mode lasing in 1D topological active arrays. Phys. Rev. Lett. 2018, 120, 113901. [Google Scholar] [CrossRef]
- Harari, G.; Bandres, M.A.; Lumer, Y.; Rechtsman, M.C.; Chong, Y.D.; Khajavikhan, M.; Christodoulides, D.N.; Segev, M. Topological insulator laser: Theory. Science 2018, 359, eaar4003. [Google Scholar] [CrossRef] [Green Version]
- Bandres, M.A.; Wittek, S.; Harari, G.; Parto, M.; Ren, J.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Topological insulator laser: Experiments. Science 2018, 359, eaar4005. [Google Scholar] [CrossRef] [Green Version]
- Savoia, S.; Castaldi, G.; Galdi, V.; Alú, A.; Engheta, N. Tunneling of obliquely incident waves through PT-symmetric epsilon-near-zero bilayers. Phys. Rev. B 2014, 89, 085105. [Google Scholar] [CrossRef]
- Shramkova, O.V.; Tsironis, G.P. Scattering properties of PT-symmetric layered periodic structures. J. Opt. 2016, 18, 105101. [Google Scholar] [CrossRef]
- Zhao, D.; Ke, S.; Liu, Q.; Wang, B.; Lu, P. Giant Goos-Hänchen shifts in non-Hermitian dielectric multilayers incorporated with graphene. Opt. Express 2018, 26, 2817–2828. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Wang, B.; Ke, S.; Long, H.; Wang, K.; Lu, P. Exceptional points in Fano-resonant graphene metamaterials. Opt. Express 2017, 25, 7203–7212. [Google Scholar] [CrossRef] [PubMed]
- Ke, S.; Wang, B.; Qin, C.; Long, H.; Wang, K.; Lu, P. Exceptional points and asymmetric mode switching in plasmonic waveguides. J. Lightwave Technol. 2016, 34, 5258–5262. [Google Scholar] [CrossRef]
- Merano, M. Optical beam shifts in graphene and single-layer boron-nitride. Opt. Lett. 2016, 41, 5780–5783. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.G.; Zhu, S.Y. Giant lateral shift of a light beam at the defect mode in one-dimensional photonic crystals. Opt. Lett. 2006, 31, 101–103. [Google Scholar] [CrossRef] [PubMed]
- Mortensen, N.A.; Gonçalves, P.A.D.; Khajavikhan, M.; Christodoulides, D.N.; Tserkezis, C.; Wolff, C. Fluctuations and noise-limited sensing near the exceptional point of parity-time-symmetric resonator systems. Optica 2018, 5, 1342–1346. [Google Scholar] [CrossRef] [Green Version]
- Wolff, C.; Tserkezis, C.; Mortensen, N.A. On the time evolution at a fluctuating exceptional point. arXiv 2018, arXiv:1810.08390. [Google Scholar] [CrossRef]
- Hayenga, W.E.; Ren, J.; Parto, M.; Wu, F.; Hokmabadi, M.P.; Wolff, C.; Khajavikhan, M. Direct generation of tunable orbital angular momentum beams in microring lasers with broadband exceptional points. arXiv 2019, arXiv:1903.10108. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Kong, W.; Zhang, P.; Li, Z.; Zhong, D. Coherent Perfect Absorption Laser Points in One-Dimensional Anti-Parity–Time-Symmetric Photonic Crystals. Appl. Sci. 2019, 9, 2738. https://doi.org/10.3390/app9132738
Wang H, Kong W, Zhang P, Li Z, Zhong D. Coherent Perfect Absorption Laser Points in One-Dimensional Anti-Parity–Time-Symmetric Photonic Crystals. Applied Sciences. 2019; 9(13):2738. https://doi.org/10.3390/app9132738
Chicago/Turabian StyleWang, Huiling, Weihao Kong, Pu Zhang, Zhongming Li, and Dong Zhong. 2019. "Coherent Perfect Absorption Laser Points in One-Dimensional Anti-Parity–Time-Symmetric Photonic Crystals" Applied Sciences 9, no. 13: 2738. https://doi.org/10.3390/app9132738
APA StyleWang, H., Kong, W., Zhang, P., Li, Z., & Zhong, D. (2019). Coherent Perfect Absorption Laser Points in One-Dimensional Anti-Parity–Time-Symmetric Photonic Crystals. Applied Sciences, 9(13), 2738. https://doi.org/10.3390/app9132738



