Efficient Transmit Delay Calculation in Ultrasound Coherent Plane-Wave Compound Imaging for Curved Array Transducers
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
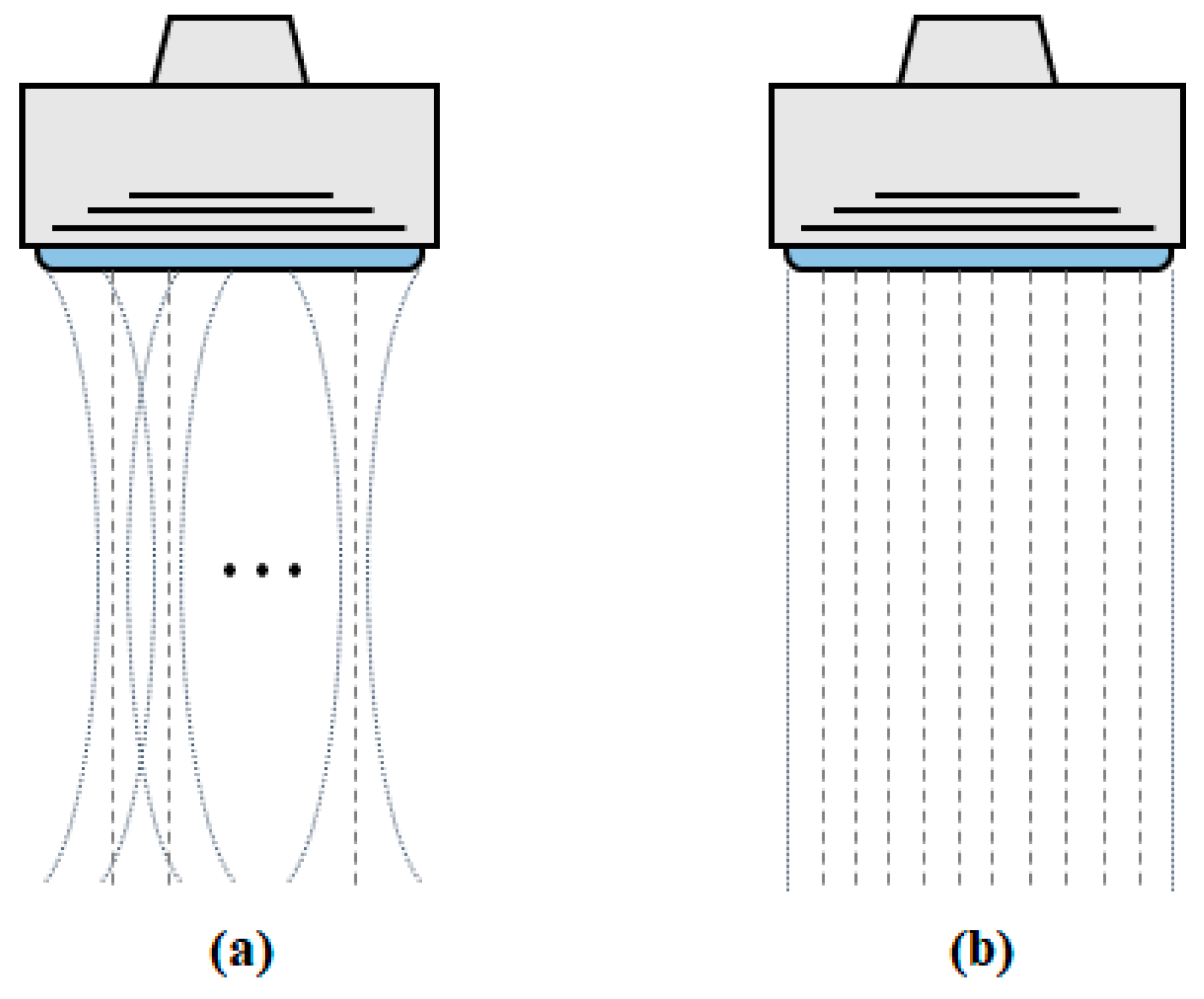
2.1. Plane-Wave Compound Imaging
2.2. Conventional Transmit Delay Calcuation
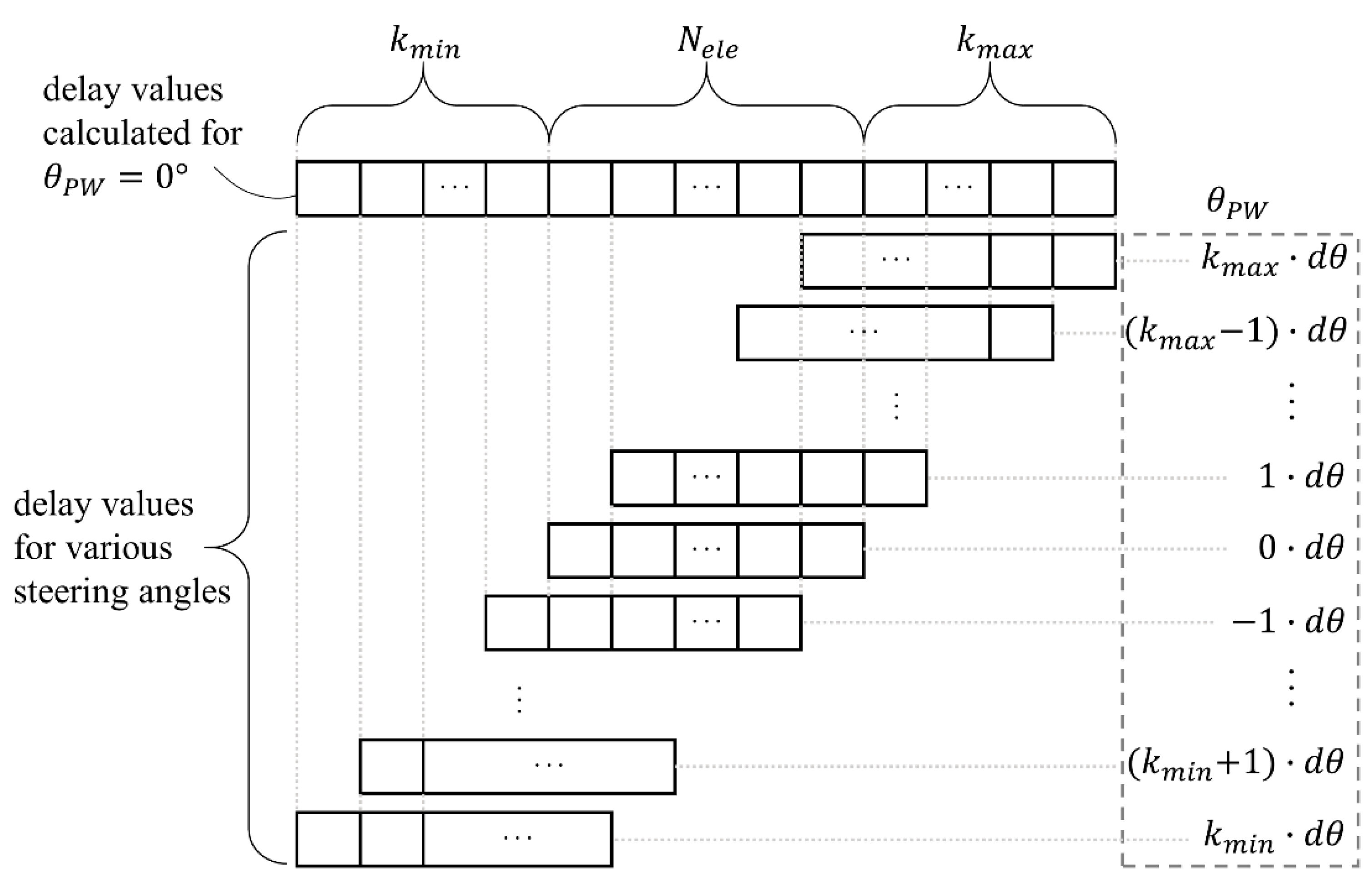
2.3. Efficient Transmit Delay Calculation
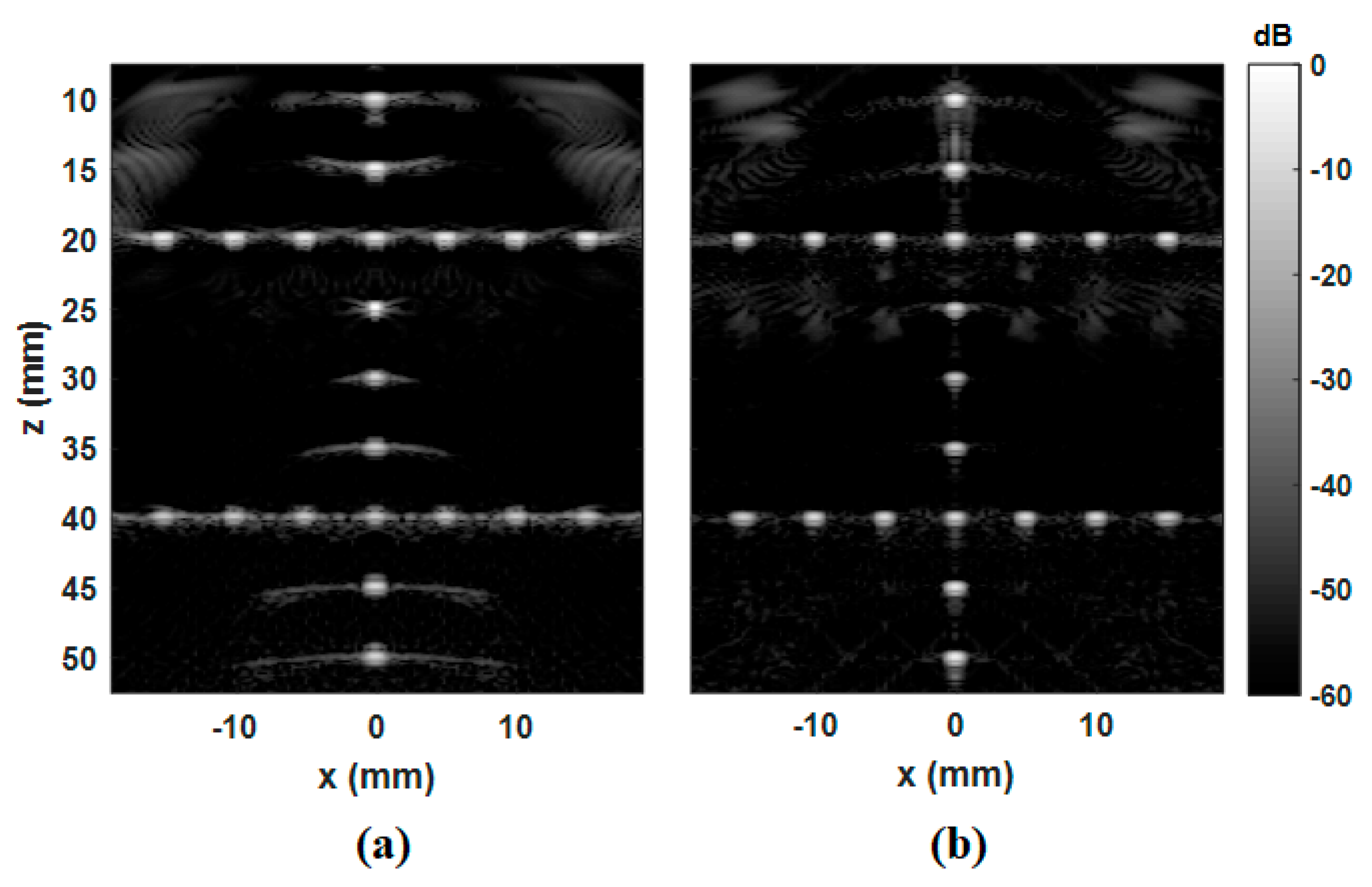
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Szabo, T. Diagnostic Ultrasound Imaging: Inside Out; Elsevier Academic Press: New York, NY, USA, 2004. [Google Scholar]
- Hoskins, P.; Martin, K.; Thrush, A. Diagnostic Ultrasound: Physics and Equipment; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Shattuck, D.P.; Weinshenker, M.D.; Smith, S.W.; von Ramm, O.T. Explososcan: A parallel processing technique for high speed ultrasound imaging with linear phased arrays. J. Acoust. Soc. Am. 1984, 75, 1273–1282. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Ramalli, A.; Jasaityte, R.; Tortoli, P.; D’hooge, J. Multi-transmit beam forming for fast cardiac imaging—Experimental validation and in vivo application. IEEE Trans. Med. Imaging 2014, 33, 1205–1219. [Google Scholar] [CrossRef] [PubMed]
- Tanter, M.; Fink, M. Ultrafast imaging in biomedical ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 102–119. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.; Kim, P.; Song, T.K. Ultrasonic sector imaging using plane wave synthetic focusing with a convex array transducer. J. Acoust. Soc. Am. 2018, 144, 2627–2644. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.; Song, T.K. Methods for grating lobe suppression in ultrasound plane wave imaging. Appl. Sci. 2018, 8, 1881. [Google Scholar] [CrossRef]
- Hasegawa, H.; Kanai, H. High-frame-rate echocardiography using diverging transmit beams and parallel receive beamforming. J. Med. Ultrason. 2011, 38, 129–140. [Google Scholar] [CrossRef] [PubMed]
- Montaldo, G.; Tanter, M.; Bercoff, J.; Benech, N.; Fink, M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 489–506. [Google Scholar] [CrossRef]
- Tanter, M.; Bercoff, J.; Sandrin, L.; Fink, M. Ultrafast compound imaging for 2-D motion vector estimation: Application to transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 1363–1374. [Google Scholar] [CrossRef]
- Bercoff, J.; Tanter, M.; Fink, M. Supersonic shear imaging: A new technique for soft tissue elasticity mapping. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 396–409. [Google Scholar] [CrossRef]
- Sandrin, L.; Tanter, M.; Catheline, S.; Fink, M. Shear modulus imaging using 2D transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 426–435. [Google Scholar] [CrossRef]
- Bercoff, J.; Montaldo, G.; Loupas, T.; Savery, D.; Mézière, F.; Fink, M.; Tanter, M. Ultrafast compound Doppler imaging: Providing full blood flow characterization. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 134–147. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Jang, W.S.; Yoo, Y. High PRF ultrafast sliding compound Doppler imaging: Fully qualitative and quantitative analysis of blood flow. Phys. Med. Biol. 2018, 63, 045004. [Google Scholar] [CrossRef] [PubMed]
- Demené, C.; Deffieux, T.; Pernot, M.; Osmanski, B.F.; Biran, V.; Gennisson, J.L.; Sieu, L.A.; Bergel, A.; Franqui, S.; Correas, J.M.; et al. Spatiotemporal clutter filtering of ultrafast ultrasound data highly increases Doppler and fUltrasound sensitivity. IEEE Trans. Med. Imaging 2015, 34, 2271–2285. [Google Scholar] [CrossRef] [PubMed]
- Song, P.; Manduca, A.; Trzasko, J.D.; Chen, S. Ultrasound small vessel imaging with block-wise adaptive local clutter filtering. IEEE Trans. Med. Imaging 2017, 36, 251–262. [Google Scholar] [CrossRef] [PubMed]
- Couture, O.; Fink, M.; Tanter, M. Ultrasound contrast plane wave imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2676–2683. [Google Scholar] [CrossRef] [PubMed]
- Couture, O.; Bannouf, S.; Montaldo, M.; Aubry, J.F.; Fink, M.; Tanter, M. Ultrafast imaging of ultrasound contrast agents. Ultrasound Med. Biol. 2009, 35, 1908–1916. [Google Scholar] [CrossRef] [PubMed]
- Errico, C.; Pierre, J.; Pezet, S.; Desailly, Y.; Lenkei, Z.; Couture, O.; Tanter, M. Ultrafast ultrasound localization microscopy for deep super-resolution vascular imaging. Nature 2015, 527, 499–502. [Google Scholar] [CrossRef]
- Bae, S.; Kim, P.; Kang, J.; Song, T.K. An optimized plane wave synthetic focusing imaging for high-resolution convex array imaging. In Proceedings of the IEEE International Ultrasonics Symposium (IUS), Taipei, Taiwan, 21–24 October 2015. [Google Scholar]
- Yiu, B.Y.S.; Tsang, I.K.H.; Yu, A.C.H. GPU-based beamformer: Fast realization of plane wave compounding and synthetic aperture imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1698–1705. [Google Scholar] [CrossRef]
- Jensen, J.A. Field: A program for simulating ultrasound systems. Med. Biol. Eng. Comput. 1996, 34 (Suppl. 1), 351–353. [Google Scholar]
- Bavu, E.; Gennisson, J.-L.; Couade, M.; Bercoff, J.; Mallet, V.; Fink, M.; Badel, A.; Vallet-Pichard, A.; Nalpas, B.; Tanter, M.; et al. Noninvasive in vivo liver fibrosis evaluation using supersonic shear imaging: A clinical study on 113 hepatitis c virus patients. Ultrasound. Med. Biol. 2011, 37, 1361–1373. [Google Scholar] [CrossRef]
- Moon, J.H.; Hwang, J.Y.; Park, J.S.; Koh, S.H.; Park, S.Y. Impact of region of interest (ROI) size on the diagnostic performance of shear wave elastography in differentiating solid breast lesions. Acta. Radiol. 2018, 59, 657–663. [Google Scholar] [CrossRef] [PubMed]
- Youk, J.H.; Son, E.J.; Han, K.; Gweon, H.M.; Kim, J.A. Performance of shear-wave elastography for breast masses using different region-of-interest (ROI) settings. Acta. Radiol. 2018, 59, 789–797. [Google Scholar] [CrossRef] [PubMed]
- Lediju, M.A.; Trahey, G.E.; Byram, B.C.; Dahl, J.J. Short-lag spatial coherence of backscattered echoes: Imaging characteristics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1377–1388. [Google Scholar] [CrossRef] [PubMed]





| Variables | Conventional | Proposed | ||
|---|---|---|---|---|
| Number of computations | Number of computations | |||
| 64 | 9 | 32 | 576 | 128 |
| 64 | 576 | 192 | ||
| 65 | 32 | 4160 | 128 | |
| 64 | 4160 | 192 | ||
| 128 | 9 | 64 | 1152 | 256 |
| 128 | 1152 | 384 | ||
| 65 | 64 | 8320 | 256 | |
| 128 | 8320 | 384 | ||
| 192 | 9 | 96 | 1728 | 384 |
| 192 | 1728 | 576 | ||
| 65 | 96 | 12,480 | 384 | |
| 192 | 12,480 | 576 | ||
| Variables | Conventional | Proposed | ||
|---|---|---|---|---|
| Computation Time (μs) | Computation Time (μs) | |||
| 128 | 9 | 64 | 19.6 ± 0.7 | 8.4 ± 0.7 |
| 128 | 19.4 ± 0.7 | 8.9 ± 0.8 | ||
| 65 | 64 | 78.6 ± 0.5 | 8.4 ± 0.7 | |
| 128 | 78.8 ± 0.8 | 8.4 ± 0.2 | ||
| 192 | 9 | 96 | 32.6 ± 0.6 | 8.5 ± 0.2 |
| 192 | 32.8 ± 0.7 | 9.1 ± 0.2 | ||
| 65 | 96 | 148.2 ± 2.4 | 8.8 ± 0.8 | |
| 192 | 149.0 ± 0.7 | 9.3 ± 0.4 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Go, D.; Kang, J.; Song, I.; Yoo, Y. Efficient Transmit Delay Calculation in Ultrasound Coherent Plane-Wave Compound Imaging for Curved Array Transducers. Appl. Sci. 2019, 9, 2752. https://doi.org/10.3390/app9132752
Go D, Kang J, Song I, Yoo Y. Efficient Transmit Delay Calculation in Ultrasound Coherent Plane-Wave Compound Imaging for Curved Array Transducers. Applied Sciences. 2019; 9(13):2752. https://doi.org/10.3390/app9132752
Chicago/Turabian StyleGo, Dooyoung, Jinbum Kang, Ilseob Song, and Yangmo Yoo. 2019. "Efficient Transmit Delay Calculation in Ultrasound Coherent Plane-Wave Compound Imaging for Curved Array Transducers" Applied Sciences 9, no. 13: 2752. https://doi.org/10.3390/app9132752
APA StyleGo, D., Kang, J., Song, I., & Yoo, Y. (2019). Efficient Transmit Delay Calculation in Ultrasound Coherent Plane-Wave Compound Imaging for Curved Array Transducers. Applied Sciences, 9(13), 2752. https://doi.org/10.3390/app9132752





