A Hybrid Model for Investigating the Effect of Scattering from Building Façade on Sound Propagation in Street Canyons
Abstract
:Featured Application
Abstract
1. Introduction
2. Calculation Model
3. Full-Scale Measurement in Real Urban Streets for Model Validation
3.1. Site Selection for Full-Scale Measurement
3.2. Measurement System and Configuration
3.3. Estimation of Acoustic Parameters of Building Façades
4. Comparison between Calculation Models and Full-Scale Measurements
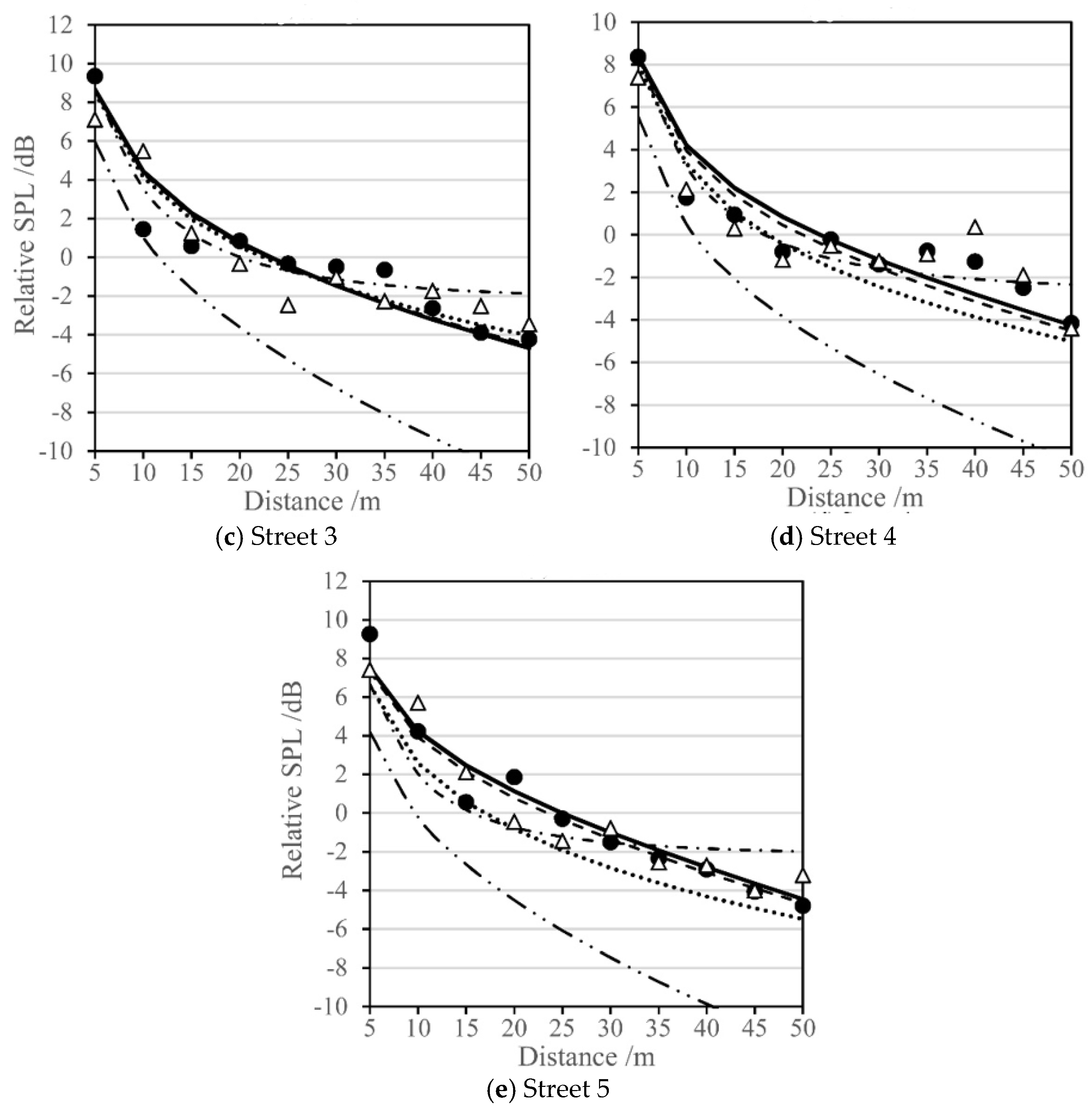
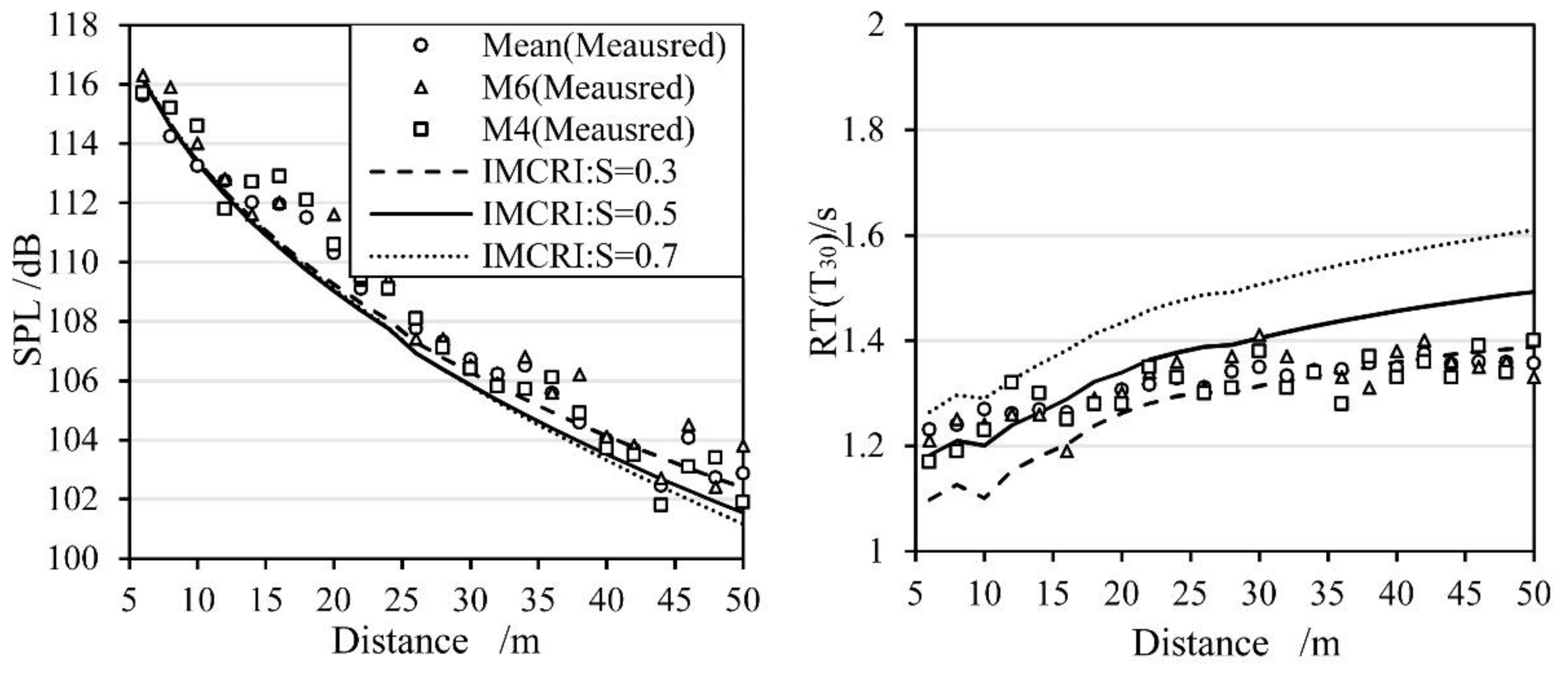
4.1. Sound Pressure Level along the Street
4.2. Reverberation Time along the Street
4.3. Comparison between Iterative Model Combining the Radiosity Method and Image Source Method (IMCRI) and the Existing Hybrid Model of Image Source Model (ISM) and Acoustic Radiosity Model (ARM)
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, P.J.; Jeon, J.Y. Evaluation of speech transmission in open public spaces affected by combined noises. J. Acoust. Soc. Am. 2011, 130, 219. [Google Scholar] [CrossRef] [PubMed]
- Miedema, H.M.; Oudshoorn, C.G. Annoyance from transportation noise: Relationships with exposure metrics DNL and DENL and their confidence intervals. Environ. Health Perspect. 2001, 109, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Morihara, T.; Sato, T.; Yano, T. Comparison of dose–response relationships between railway and road traffic noises: The moderating effect of distance. J. Sound Vib. 2004, 277, 559–565. [Google Scholar] [CrossRef]
- Muzet, A. Environmental noise, sleep and health. Sleep Med. Rev. 2007, 11, 135–142. [Google Scholar] [CrossRef] [PubMed]
- Babisch, W.; Beule, B.; Schust, M.; Kersten, N.; Ising, H. Traffic Noise and Risk of Myocardial Infarction. Epidemiology 2005, 16, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Van Kempen, E.; Babisch, W. The quantitative relationship between road traffic noise and hypertension: A meta-analysis. J. Hypertens. 2012, 30, 1075–1086. [Google Scholar] [CrossRef]
- Hui, M.; Shan, S. An Experimental Study: The Restorative Effect of Soundscape Elements in a Simulated Open-Plan Office. Acta Acust. United Ac. 2018, 104, 106–115. [Google Scholar]
- Davis, M.J.M.; Tenpierik, M.J.; Ramírez, F.R.; Pérez, M.E. More than just a Green Facade: The sound absorption properties of a vertical garden with and without plants. Build. Environ. 2017, 116, 64–72. [Google Scholar] [CrossRef]
- Van Renterghem, T.; Botteldooren, D. In-situ measurements of sound propagating over extensive green roofs. Build. Environ. 2011, 46, 729–738. [Google Scholar] [CrossRef] [Green Version]
- Guillaume, G.; Gauvreau, B.; Hermite, P.L. Numerical study of the impact of vegetation coverings on sound levels and time decays in a canyon street model. Sci. Total Environ. 2015, 502, 22–30. [Google Scholar] [CrossRef]
- Van Renterghem, T.; Salomons, E.; Botteldooren, D. Parameter study of sound propagation between city canyons with a coupled FDTD-PE model. Appl. Acoust. 2006, 67, 487–510. [Google Scholar] [CrossRef] [Green Version]
- Echevarria Sanchez, G.M.; Van Renterghem, T.; Thomas, P.; Botteldooren, D. The effect of street canyon design on traffic noise exposure along roads. Build. Environ. 2016, 97, 96–110. [Google Scholar] [CrossRef] [Green Version]
- Le Pollès, T.; Picaut, J.; Bérengier, M.; Bardos, C. Sound field modeling in a street canyon with partially diffusely reflecting boundaries by the transport theory. J. Acoust. Soc. Am. 2004, 116, 2969–2983. [Google Scholar] [CrossRef]
- Badino, E.; Manca, R.; Shtrepi, L.; Calleri, C.; Astolfi, A. Effect of façade shape and acoustic cladding on reduction of leisure noise levels in a street canyon. Build. Environ. 2019, 157, 242–256. [Google Scholar] [CrossRef]
- Lee, P.J.; Kang, J. Effect of height-to-width ratio on the sound propagation in urban streets. Acta Acust. United Ac. 2015, 101, 73–87. [Google Scholar] [CrossRef]
- Radwan, M.M.; Oldham, D.J. The prediction of noise from urban traffic under interrupted flow conditions. Appl. Acoust. 1987, 21, 163–185. [Google Scholar] [CrossRef]
- Can, A.; Fortin, N.; Picaut, J. Accounting for the effect of diffuse reflections and fittings within street canyons, on the sound propagation predicted by ray tracing codes. Appl. Acoust. 2015, 96, 83–93. [Google Scholar] [CrossRef]
- Kang, J. Sound propagation in street canyons: Comparison between diffusely and geometrically reflecting boundaries. J. Acoust. Soc. Am. 2000, 107, 1394–1404. [Google Scholar] [CrossRef]
- Onaga, H.; Rindel, J.H. Acoustic characteristics of urban streets in relation to scattering caused by building facades. Appl. Acoust. 2007, 68, 310–325. [Google Scholar] [CrossRef]
- Meng, Y.; Kang, J. Combined Ray-tracing and Radiosity Simulation for Urban Open Spaces. In Proceedings of the 19th International Congress on Acoustics, Madrid, Spain, 2–7 September 2007; pp. 2–7. [Google Scholar]
- Lyon, R.H. Role of multiple reflections and reverberation in urban noise propagation. J. Acoust. Soc. Am. 1974, 55, 493–503. [Google Scholar] [CrossRef]
- Schröder, D.; Pohl, A. Modeling (Non-)uniform scattering distributions in geometrical acoustics. In Proceedings of the Meetings on Acoustics, Montreal, QC, Canada, 2–7 June 2013; pp. 1–9. [Google Scholar]
- Howell, J.R.; Siegel, R.; Mengüç, M.P. Thermal radiation heat transfer, 2nd ed.; Hemisphere: Washington, DC, USA, 1981. [Google Scholar]
- Kang, J. Numerical modelling of the sound fields in urban streets with diffusely reflecting boundaries. J. Sound Vib. 2002, 258, 793–813. [Google Scholar] [CrossRef]
- Korany, N.; Blauert, J.; Alim, O.A. Acoustic simulation of rooms with boundaries of partially specular reflectivity. Appl. Acoust. 2001, 62, 875–887. [Google Scholar] [CrossRef]
- Ismail, M.R.; Oldham, D.J. A scale model investigation of sound reflection from building façades. Appl. Acoust. 2005, 66, 123–147. [Google Scholar] [CrossRef]
- Wiener, F.M.; Malme, C.I.; Gogos, C.M. Sound propagation in urban areas. J. Acoust. Soc. Am. 1965, 37, 738. [Google Scholar] [CrossRef]
- Yeow, K.W. External reverberation times observed in built-up areas. J. Sound Vib. 1976, 48, 438–440. [Google Scholar] [CrossRef]
- Yeow, K.W. Decay of sound levels with distance from a steady source observed in a built-up area. J. Sound Vib. 1977, 52, 151–154. [Google Scholar] [CrossRef]
- Picaut, J.; Le Pollès, T.; L’Hermite, P.; Gary, V. Experimental study of sound propagation in a street. Appl. Acoust. 2005, 66, 149–173. [Google Scholar] [CrossRef]
- Horoshenkov, V.; Hothersall, C.; Mercy, E. Scale modelling of sound propagation in a city street canyon. J. Sound Vib. 1999, 223, 795–819. [Google Scholar] [CrossRef]
- Picaut, J.; Simon, L. A scale model experiment for the study of sound propagation in urban areas. Appl. Acoust. 2001, 62, 327–340. [Google Scholar] [CrossRef]
- Hornikx, M.; Forssén, J. A scale model study of parallel urban canyons. Acta Acust. United Ac. 2008, 94, 265–281. [Google Scholar] [CrossRef]
- Tang, S.K.; Piippo, K.E. Sound fields inside street canyons with inclined flanking building facades. In Proceedings of the 161st Meeting Acoustical Society of America 2011, Seattle, WA, USA, 23–27 May 2011; Acoustical Society of America: Seattle, WA, USA, 2011; Volume 12, pp. 1–7. [Google Scholar]
- Jang, H.S.; Lee, S.C.; Jeon, J.Y.; Kang, J. Evaluation of road traffic noise abatement by vegetation treatment in a 1:10 urban scale model. J. Acoust. Soc. Am. 2015, 138, 3884–3895. [Google Scholar] [CrossRef] [PubMed]
- Jang, H.S.; Kim, H.J.; Jeon, J.Y. Scale-model method for measuring noise reduction in residential buildings by vegetation. Build. Environ. 2015, 86, 81–88. [Google Scholar] [CrossRef]
- Le Pollès, T.; Picaut, J.; Colle, S.; Bérengier, M.; Bardos, C. Sound-field modeling in architectural acoustics by a transport theory: Application to street canyons. Phys. Rev. E 2005, 72, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Li, K.M.; Lai, C.Y.C. A note on noise propagation in street canyons. J. Acoust. Soc. Am. 2009, 126, 644–655. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.H.; Jang, H.S.; Jeon, J.Y. Characterizing diffusive surfaces using scattering and diffusion coefficients. Appl. Acoust. 2011, 72, 899–905. [Google Scholar] [CrossRef]
- Schmich-Yamane, I.; Embrechts, J.-J.; Muller-Trapet, M.; Rougier, C.; Malgrange, M.; Vorlander, M. Prediction and measurement of the random-incidence scattering coefficient of periodic reflective rectangular diffuser profiles. In Proceedings of the International Congress on Acoustics, Montreal, QC, Canada, 2–7 June 2013; Acoustical Society of America: Montreal, QC, Canada, 2013; Volume 19, pp. 1–9. [Google Scholar]
- Lin, F.; Hong, P.; Lee, C. An experimental investigation into the sound-scattering performance of wooden diffusers with different structures. Appl. Acoust. 2010, 71, 68–78. [Google Scholar] [CrossRef]
- Yong, J.; Chan, S.; Vorla, M. Development of scattering surfaces for concert halls. Appl. Acoust. 2004, 65, 341–355. [Google Scholar] [CrossRef]
- Embrechts, J.J.; Billon, A. Theoretical Determination of the Random-Incidence Scattering Coefficients of Infinite Rigid Surfaces with a Periodic Rectangular Roughness Profile. Acta Acust. United Ac. 2011, 97, 607–617. [Google Scholar] [CrossRef]
- Shtrepi, L. Investigation on the diffusive surface modeling detail in geometrical acoustics based simulations. J. Acoust. Soc. Am. 2019, 145, EL215–EL221. [Google Scholar] [CrossRef] [Green Version]
- Iu, K.K.; Li, K.M. The propagation of sound in narrow street canyons. J. Acoust. Soc. Am. 2002, 112, 537–550. [Google Scholar] [CrossRef]
- Richoux, O.; Ayrault, C.; Pelat, a.; Félix, S.; Lihoreau, B. Effect of the open roof on low frequency acoustic propagation in street canyons. Appl. Acoust. 2010, 71, 731–738. [Google Scholar] [CrossRef] [Green Version]



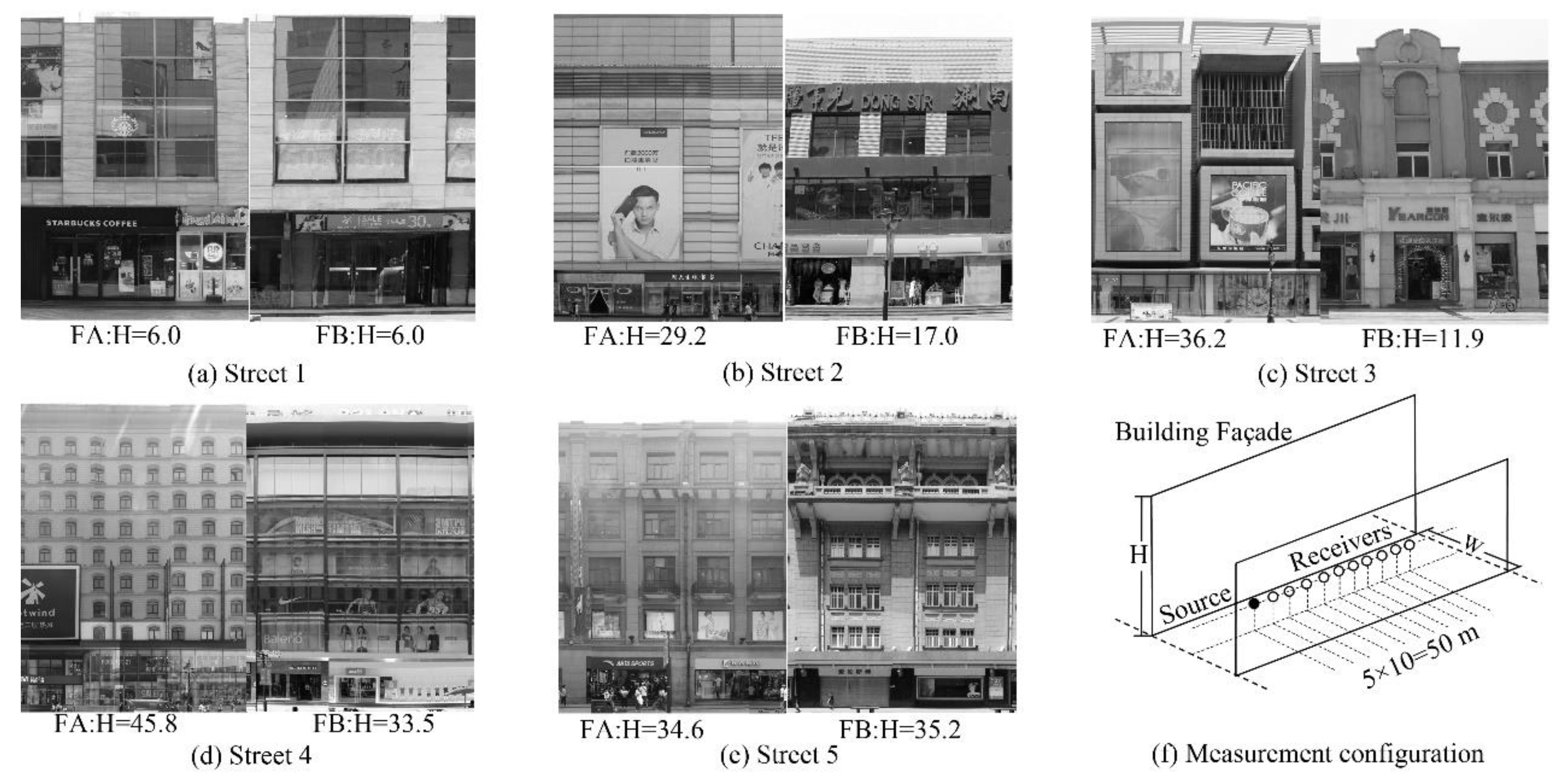





| Street Name | Coverage Density | Estimated Scattering Coefficient | ||||||
|---|---|---|---|---|---|---|---|---|
| Façade A | Façade B | Façade A | Façade B | |||||
| Sr | Sh | Sg | Sr | Sh | Sg | |||
| Street 1 | 2.00% | 7.00% | 0.08 | 0.07 | 0.09 | 0.17 | 0.16 | 0.23 |
| Street 2 | 6.50% | 15.00% | 0.16 | 0.15 | 0.22 | 0.30 | 0.28 | 0.42 |
| Street 3 | 7.10% | 10.60% | 0.17 | 0.16 | 0.23 | 0.23 | 0.22 | 0.32 |
| Street 4 | 35.00% | 18.00% | 0.52 | 0.52 | 0.71 | 0.34 | 0.33 | 0.48 |
| Street 5 | 37.00% | 54.00% | 0.53 | 0.54 | 0.73 | 0.58 | 0.64 | 0.74 |
| Time Cost/s | Street 1: W = 15; H = 6 | Street 6: W = 16; H = 35 | ||||
|---|---|---|---|---|---|---|
| S = 0.05 | S = 0.5 | S = 0.95 | S = 0.05 | S = 0.5 | S = 0.95 | |
| EHM | 53 | 97 | 102 | 1827 | 2258 | 2576 |
| IMCRI | 44 | 96 | 153 | 5016 | 15891 | 14491 |
| Ratio (IMCRI/EHM) | 0.8 | 1.0 | 1.5 | 2.7 | 7.0 | 5.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Ma, H.; Kang, J. A Hybrid Model for Investigating the Effect of Scattering from Building Façade on Sound Propagation in Street Canyons. Appl. Sci. 2019, 9, 2803. https://doi.org/10.3390/app9142803
Yu B, Ma H, Kang J. A Hybrid Model for Investigating the Effect of Scattering from Building Façade on Sound Propagation in Street Canyons. Applied Sciences. 2019; 9(14):2803. https://doi.org/10.3390/app9142803
Chicago/Turabian StyleYu, Boya, Hui Ma, and Jian Kang. 2019. "A Hybrid Model for Investigating the Effect of Scattering from Building Façade on Sound Propagation in Street Canyons" Applied Sciences 9, no. 14: 2803. https://doi.org/10.3390/app9142803
APA StyleYu, B., Ma, H., & Kang, J. (2019). A Hybrid Model for Investigating the Effect of Scattering from Building Façade on Sound Propagation in Street Canyons. Applied Sciences, 9(14), 2803. https://doi.org/10.3390/app9142803







