Analytical Study of Reinforced Concrete Beams Tested under Quasi-Static and Impact Loadings
Abstract
:1. Introduction
2. Materials and Methods
2.1. Quasi-Static Loading
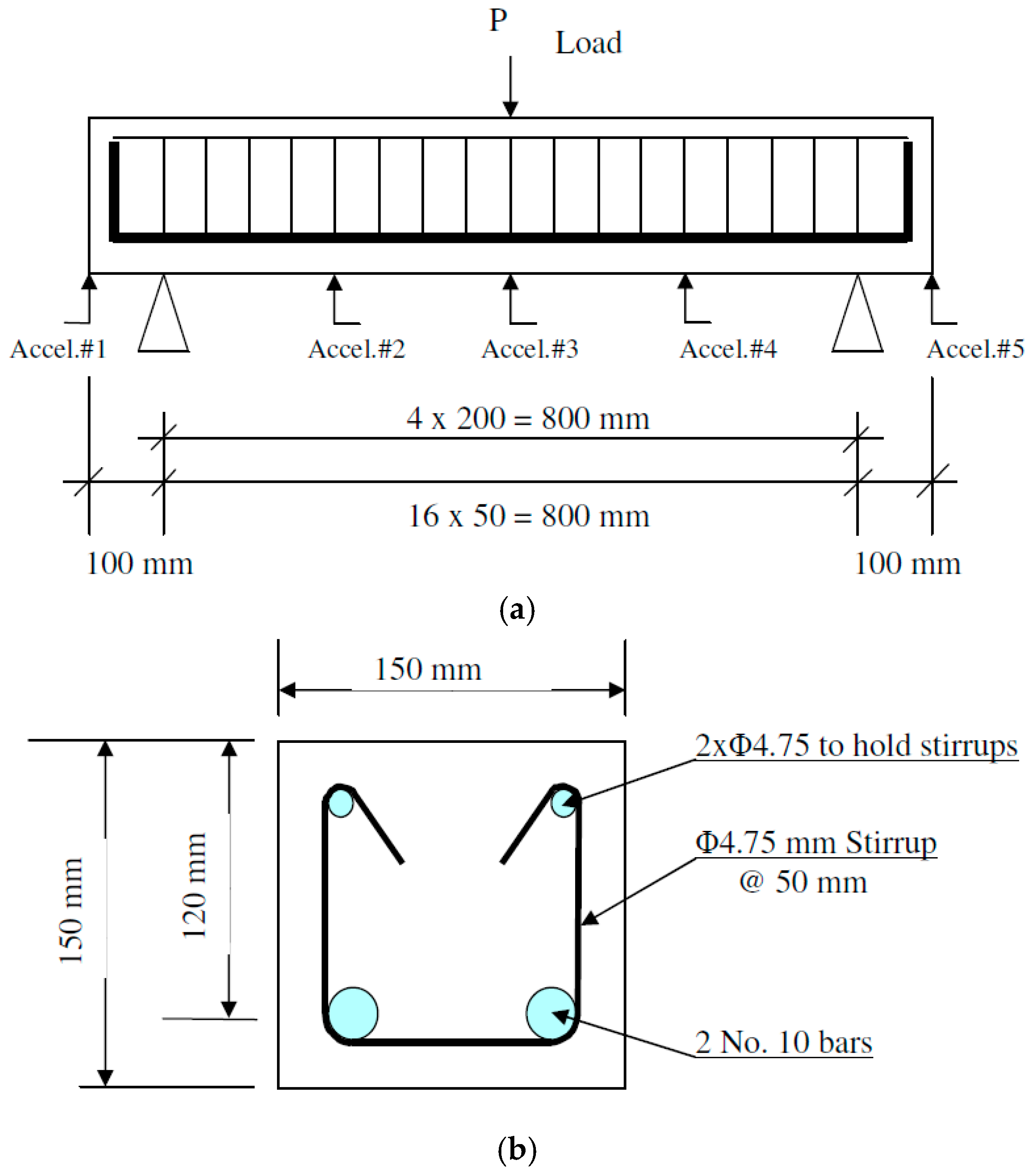
2.2. Impact Loading
3. Finite Element Model (FEM)
4. Results and Discussion
5. Conclusions
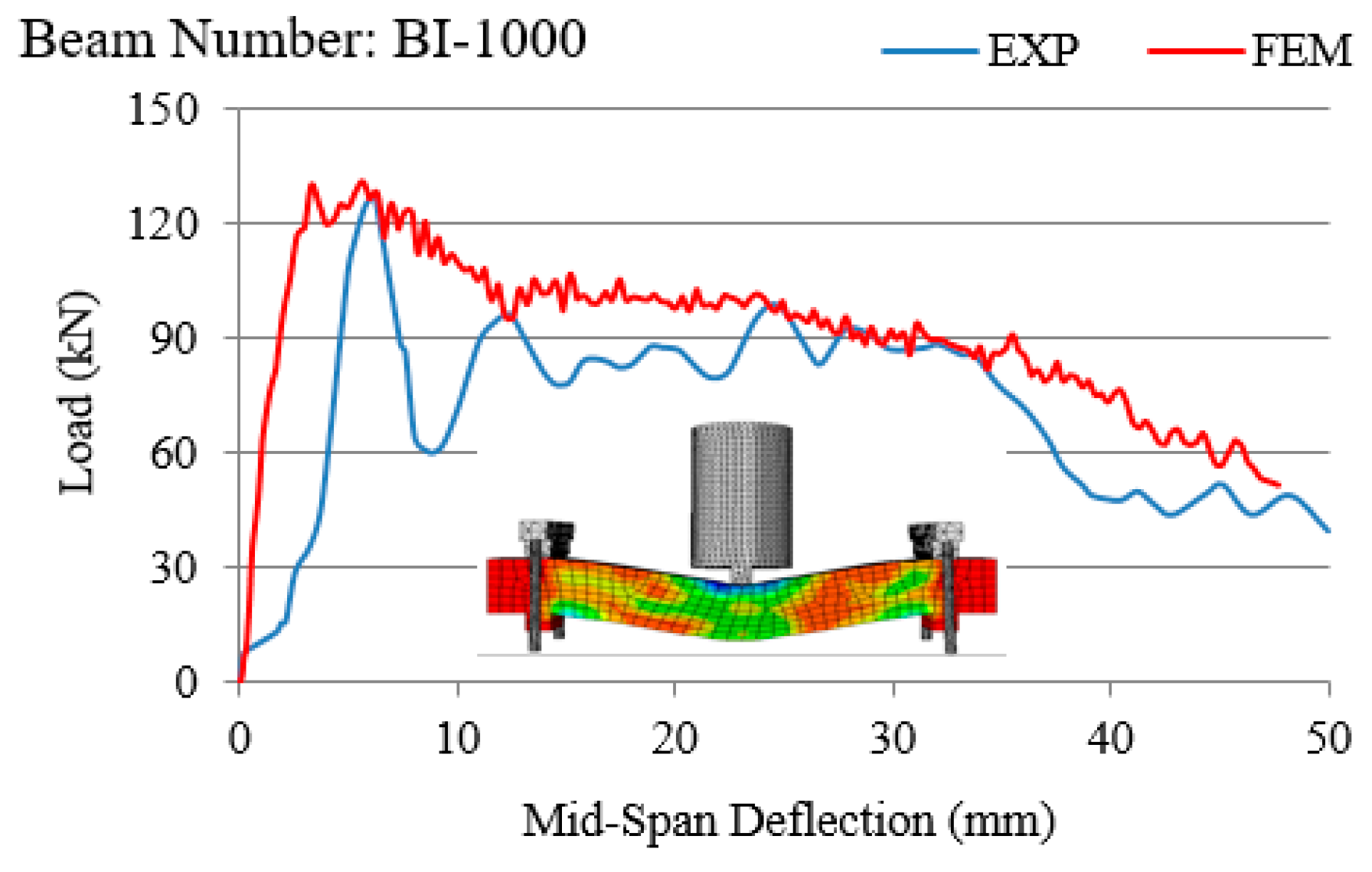
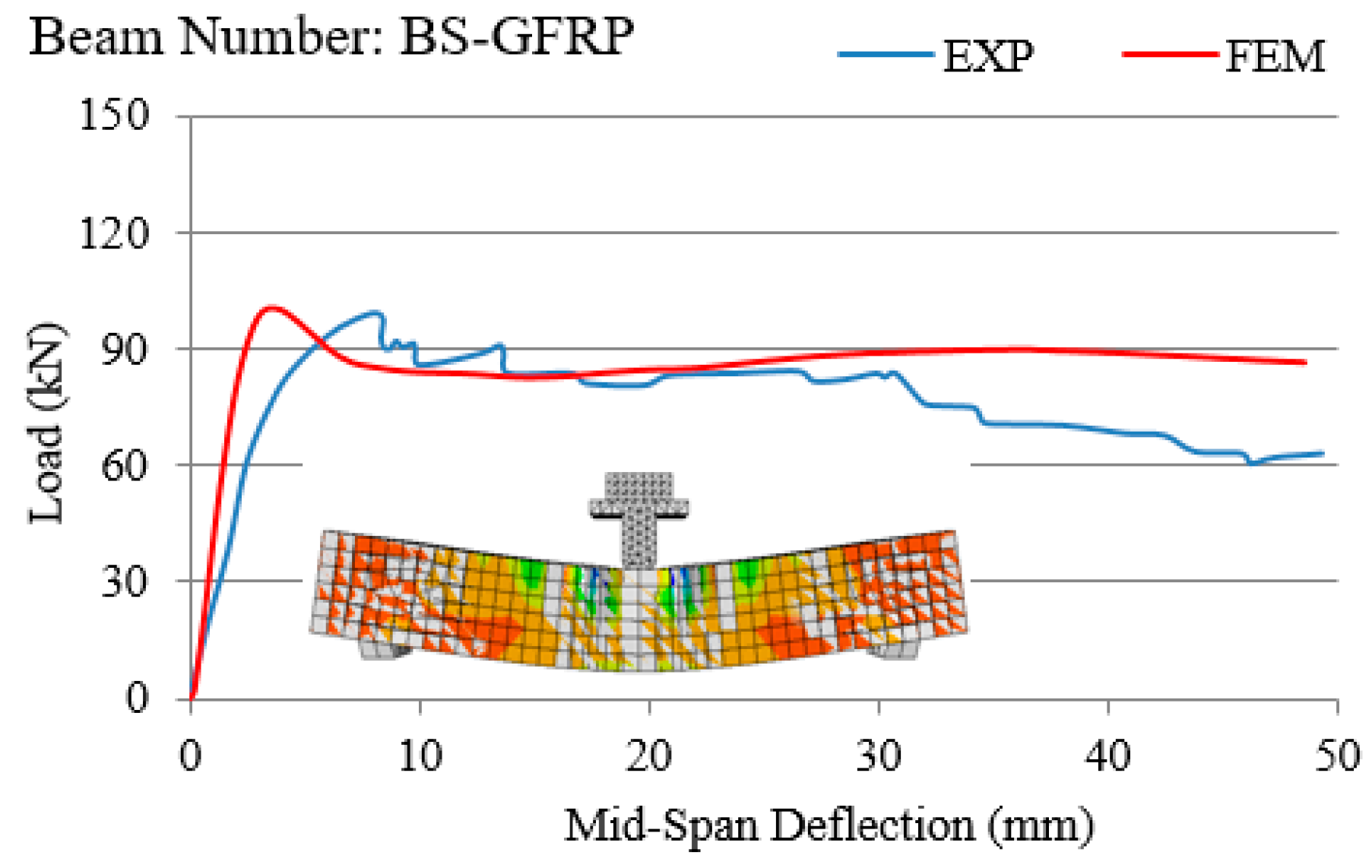
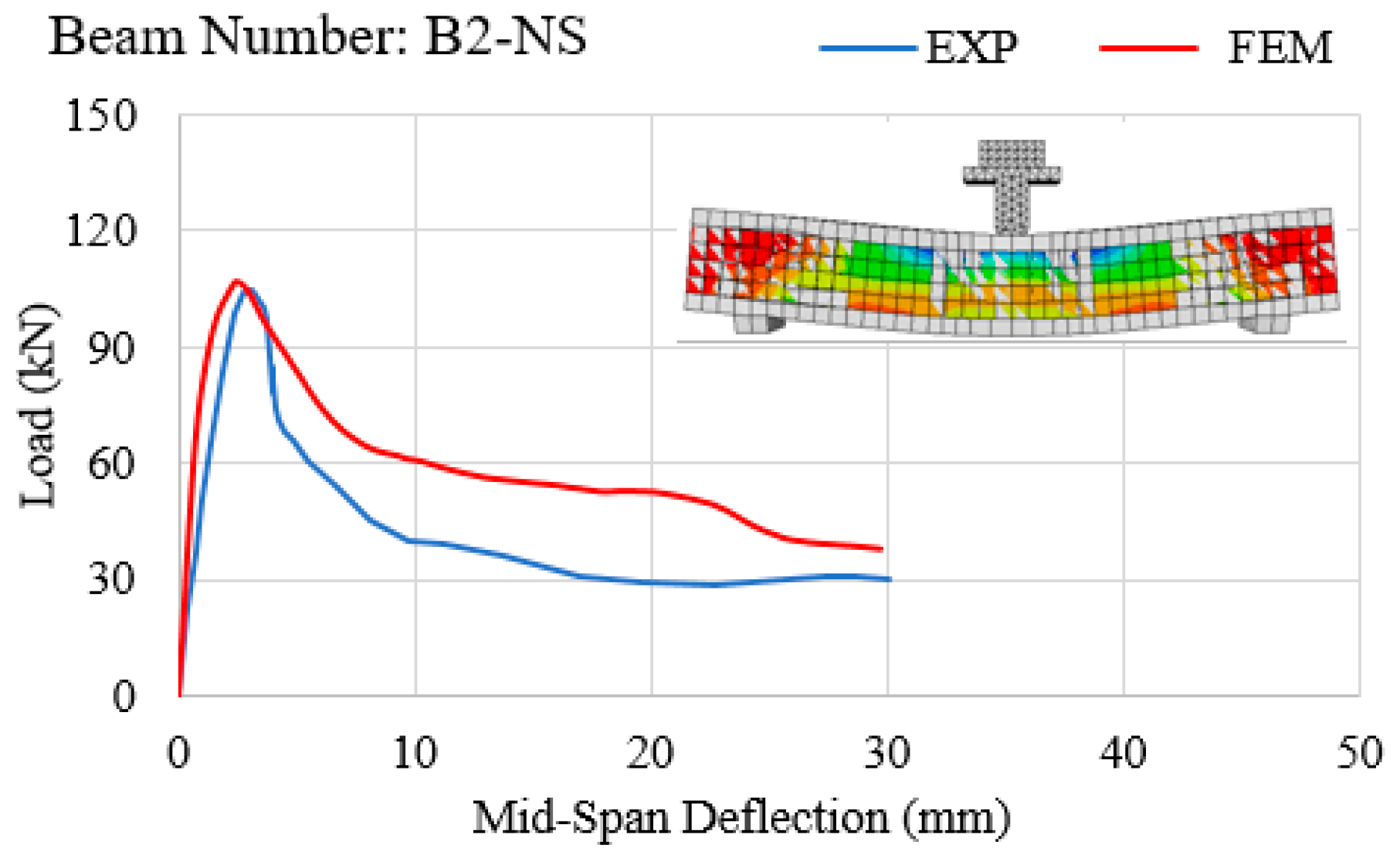
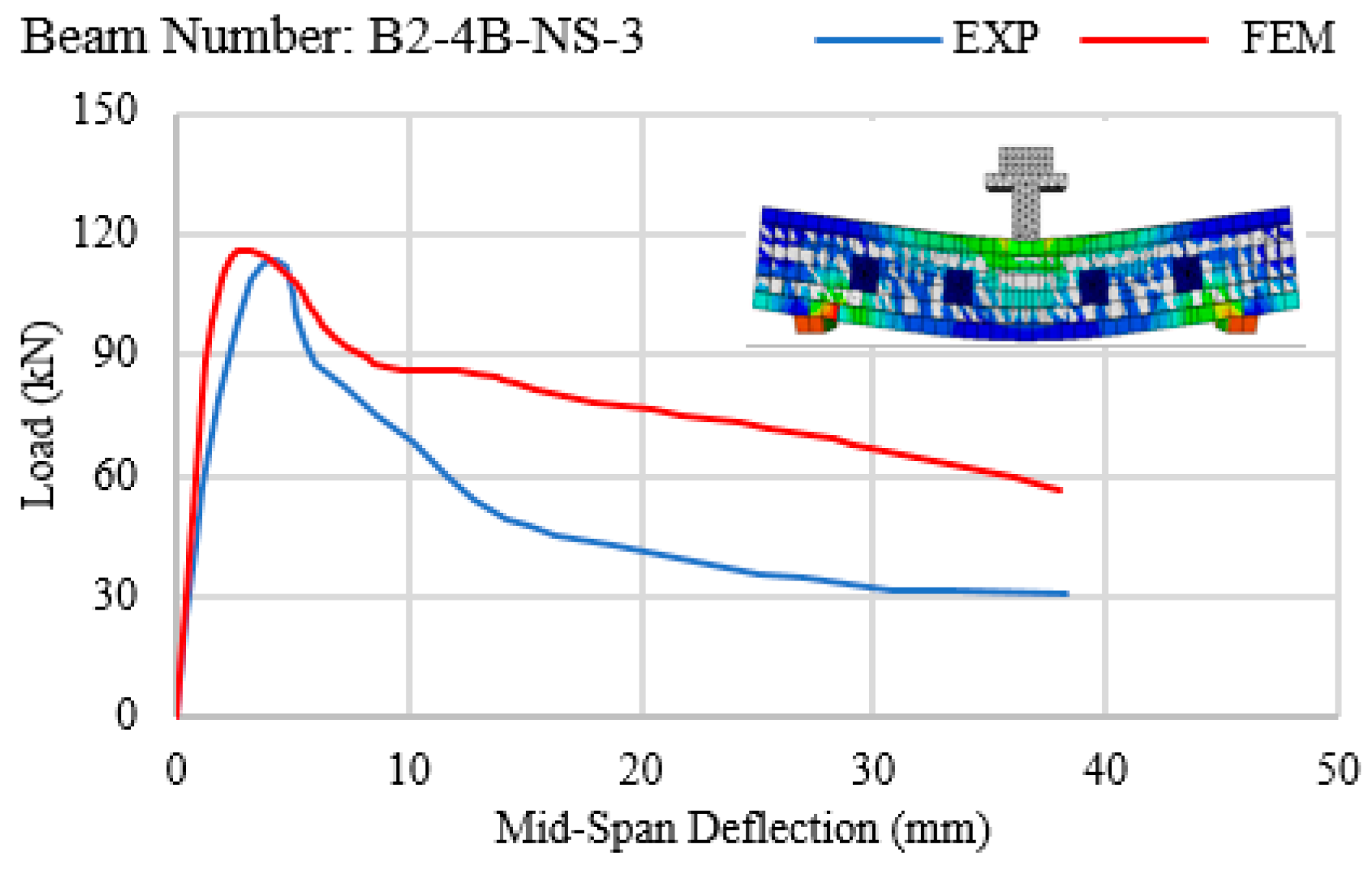
- Load vs. mid-span displacement curves obtained from finite element models generated by ABAQUS software, for both quasi-static and impact loadings, suggest close correspondence with laboratory results.
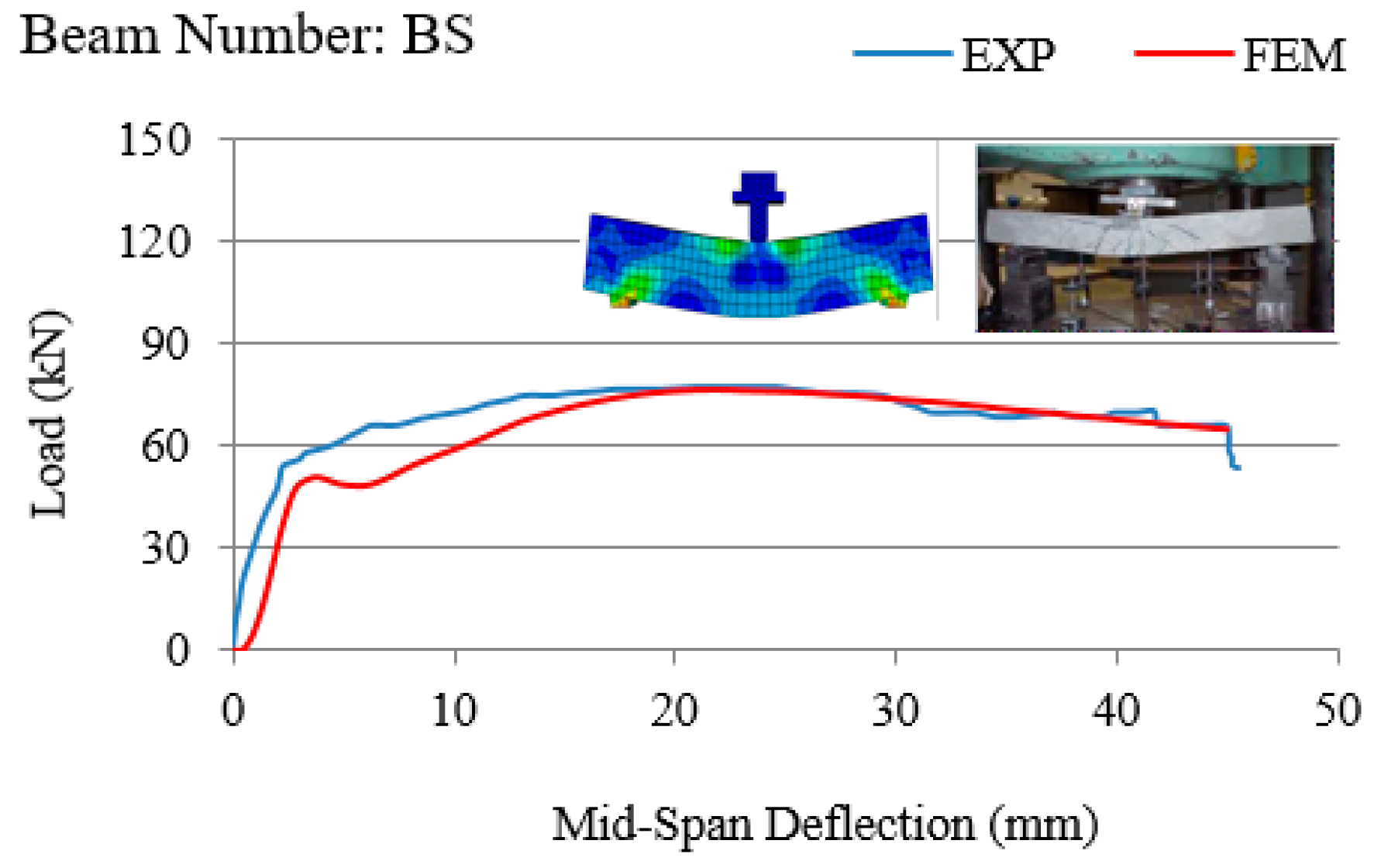
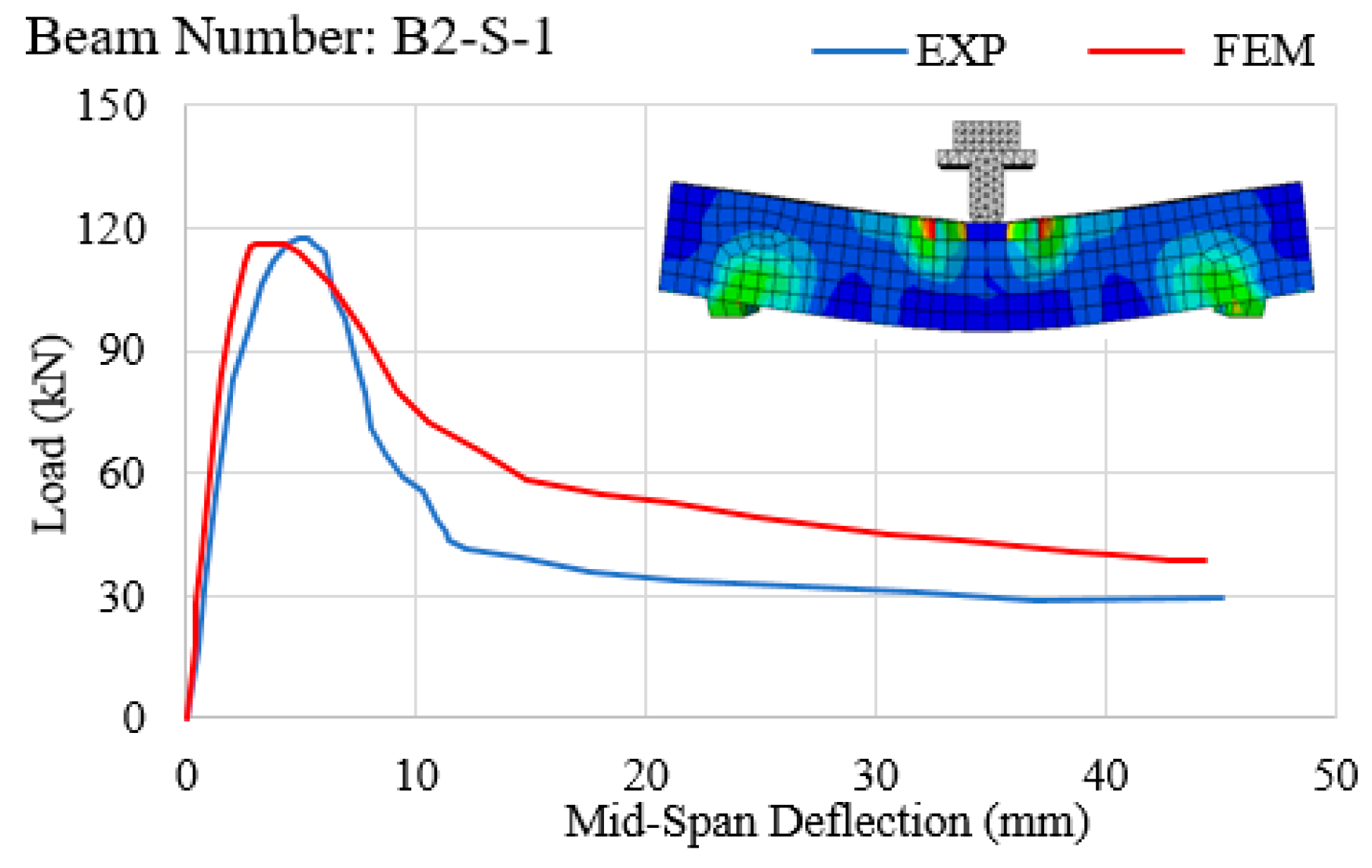
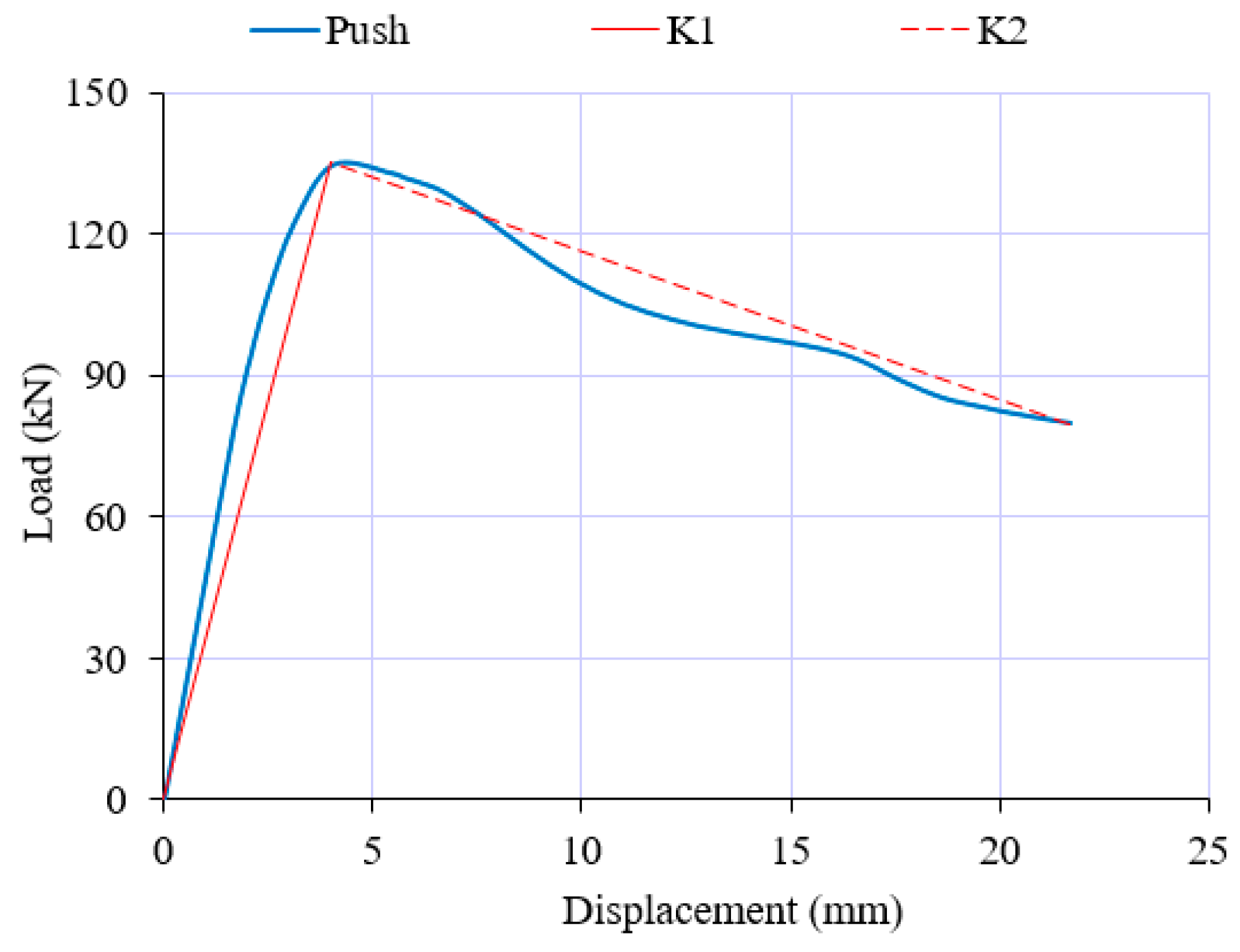
- In quasi-static loading on an RC beam (Figure 6) with an adequate number of stirrups, both ABAQUS software and laboratory results verified that the stress in longitudinal tension reinforcements exceeded the yield stress of steel, and the load-carrying capacity of the beam increased subsequent to the yield of tensile steel. This implies that the failure of the RC beam presented in Figure 6 is flexural.
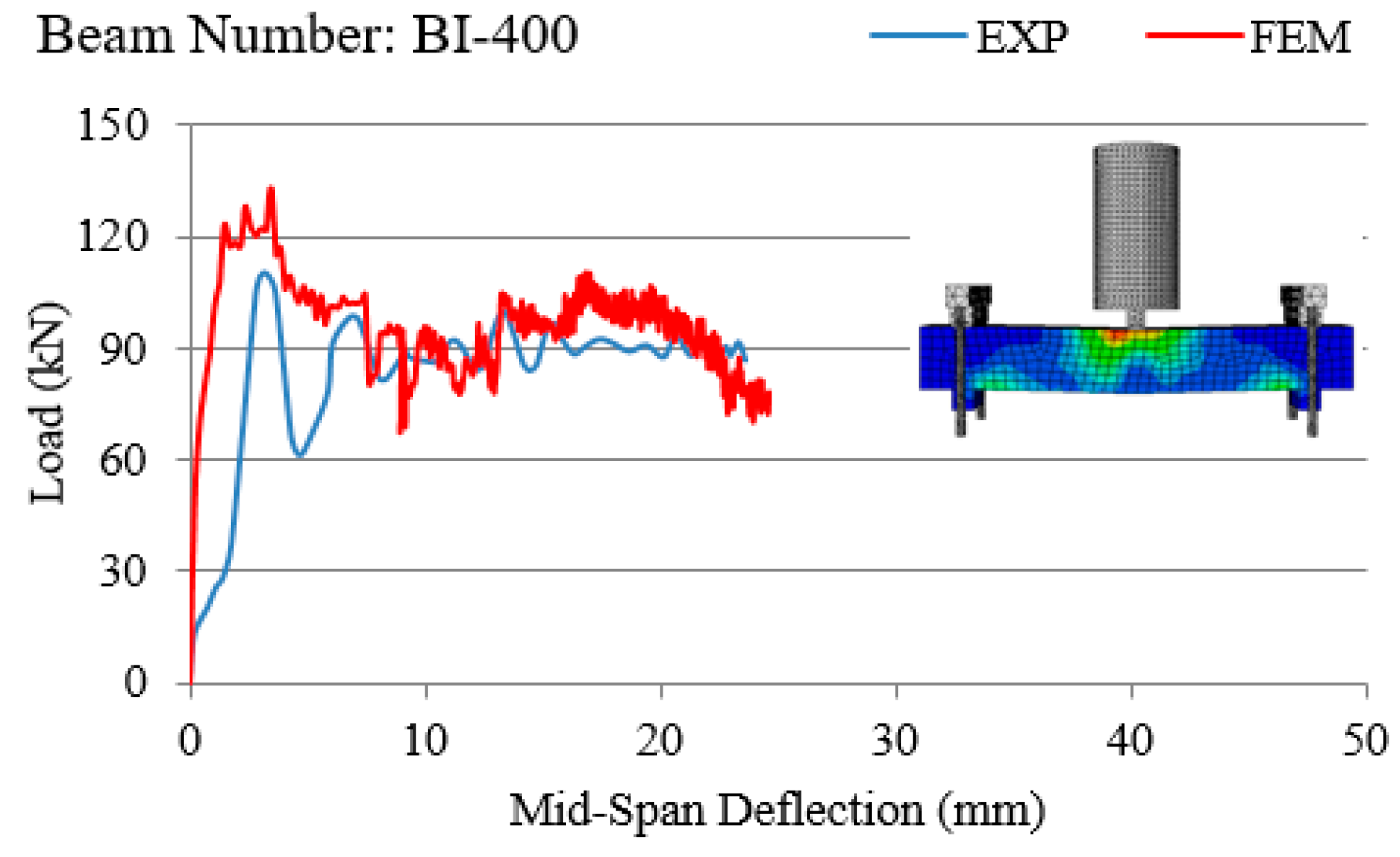
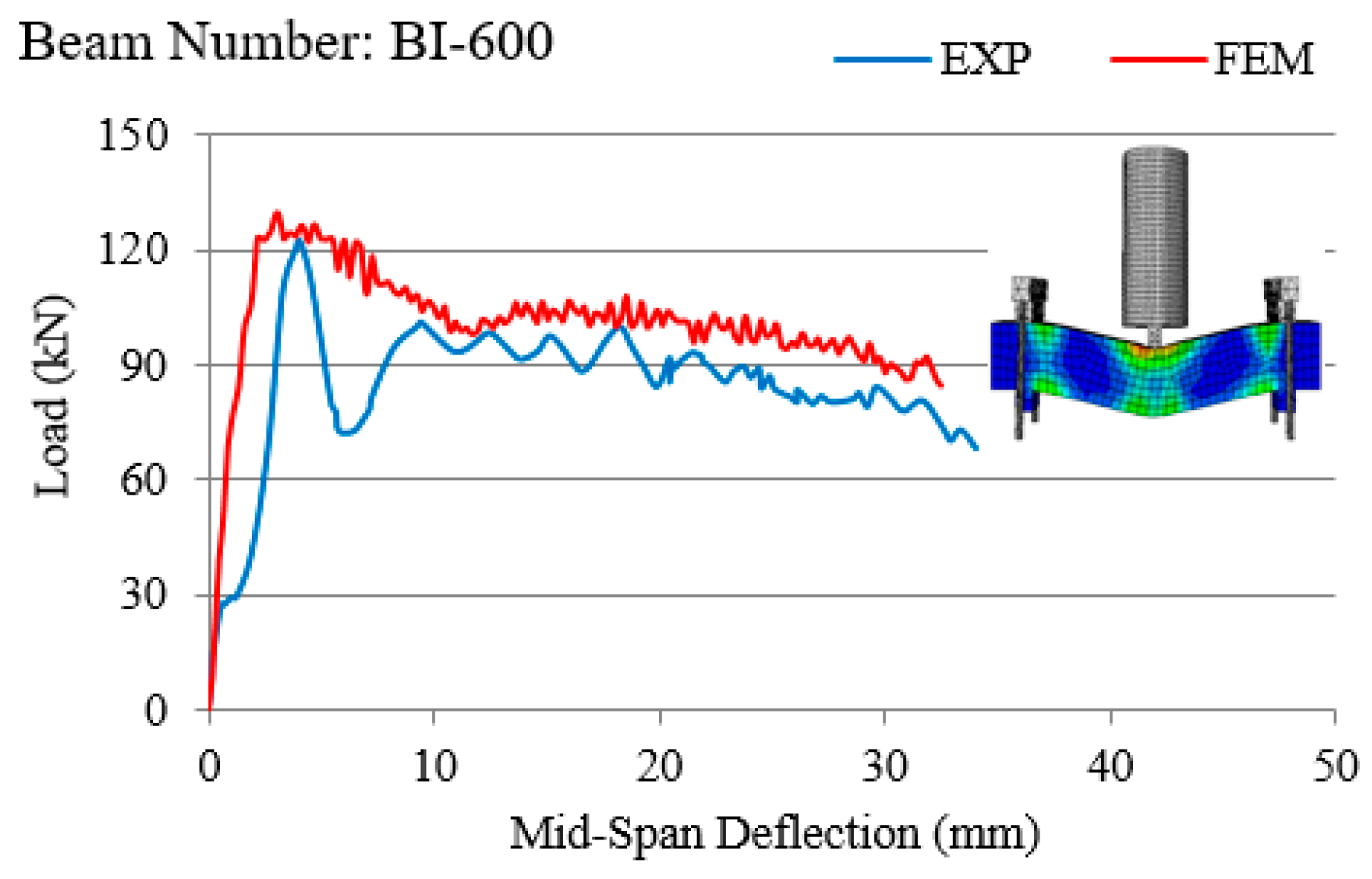
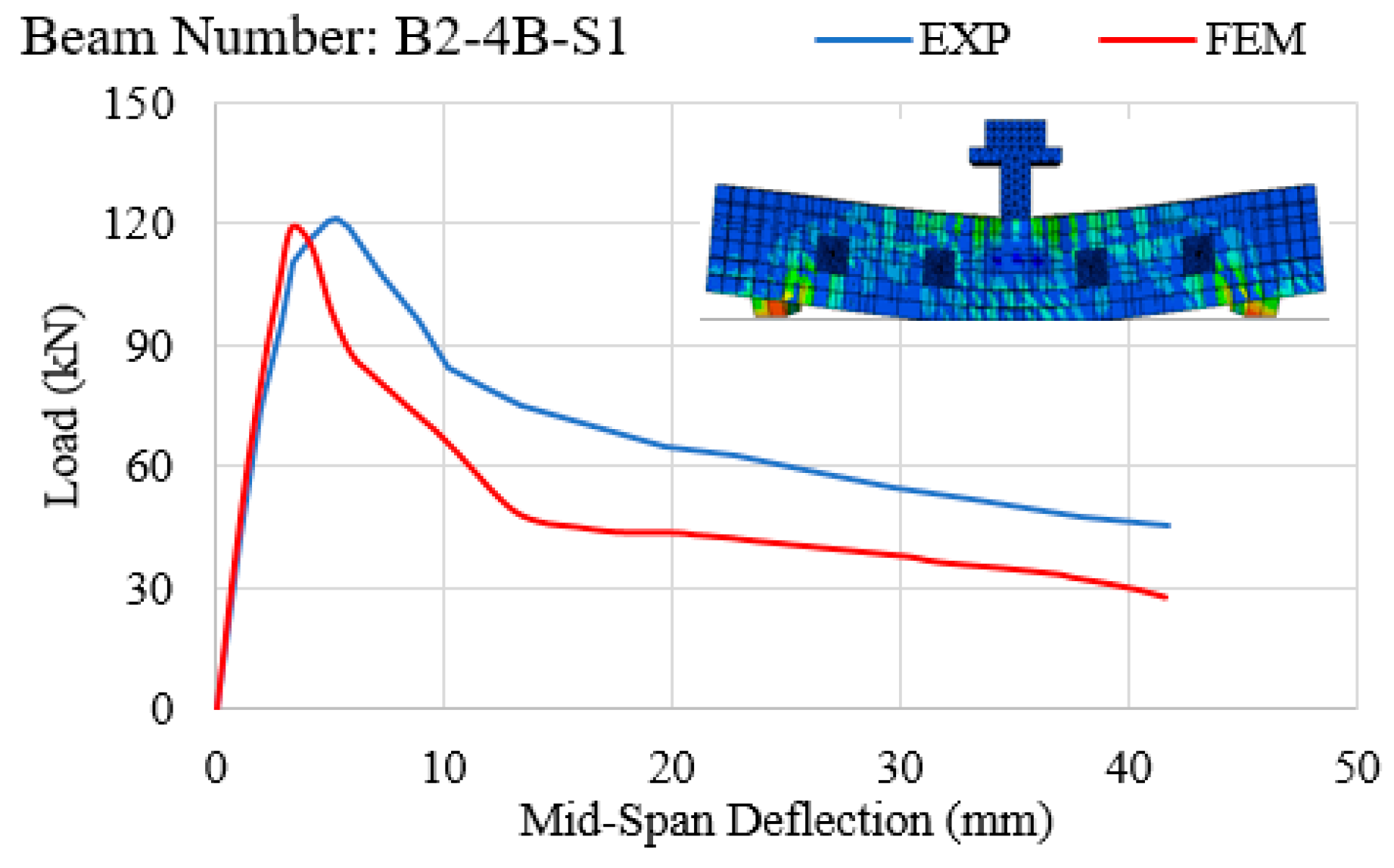
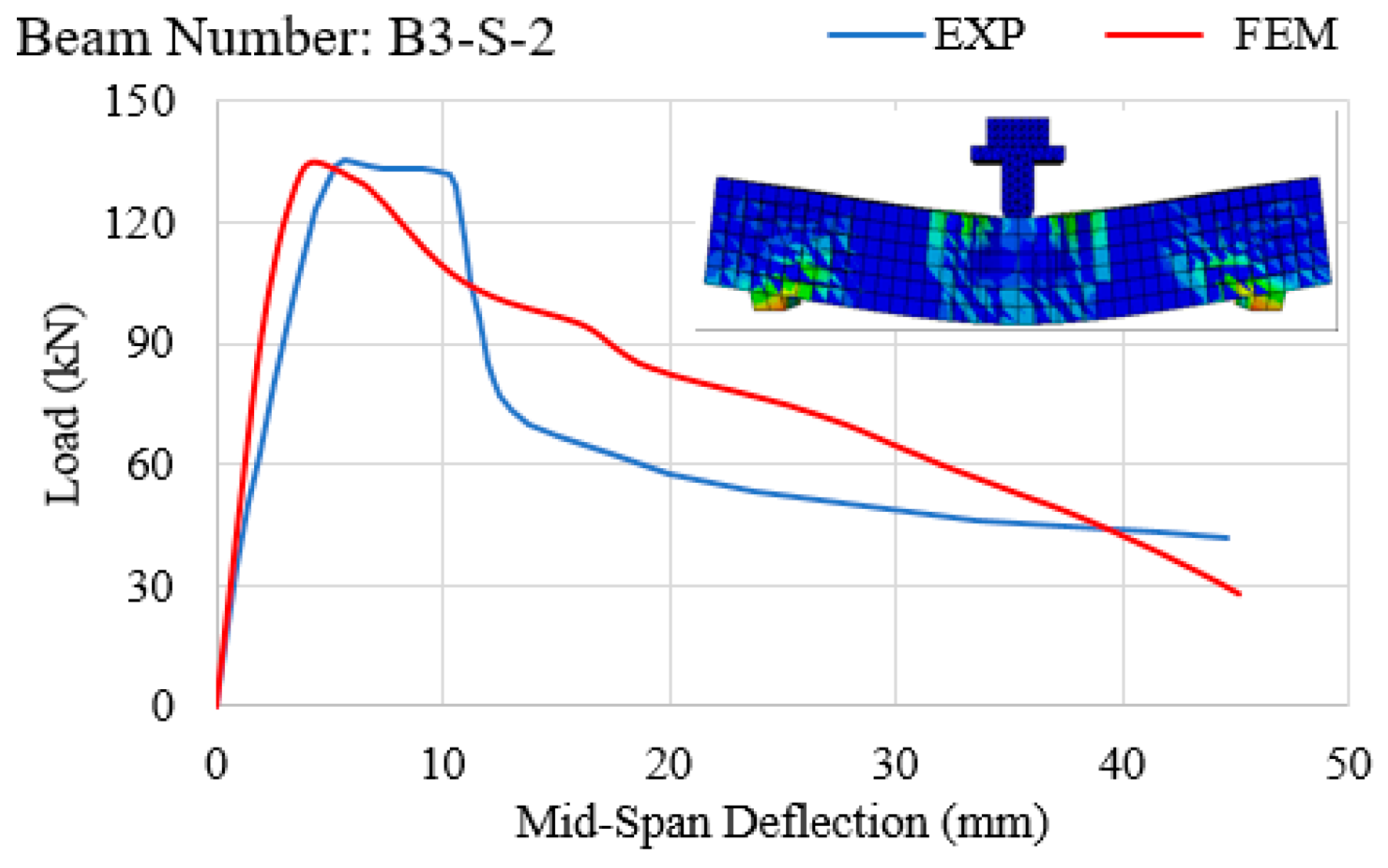
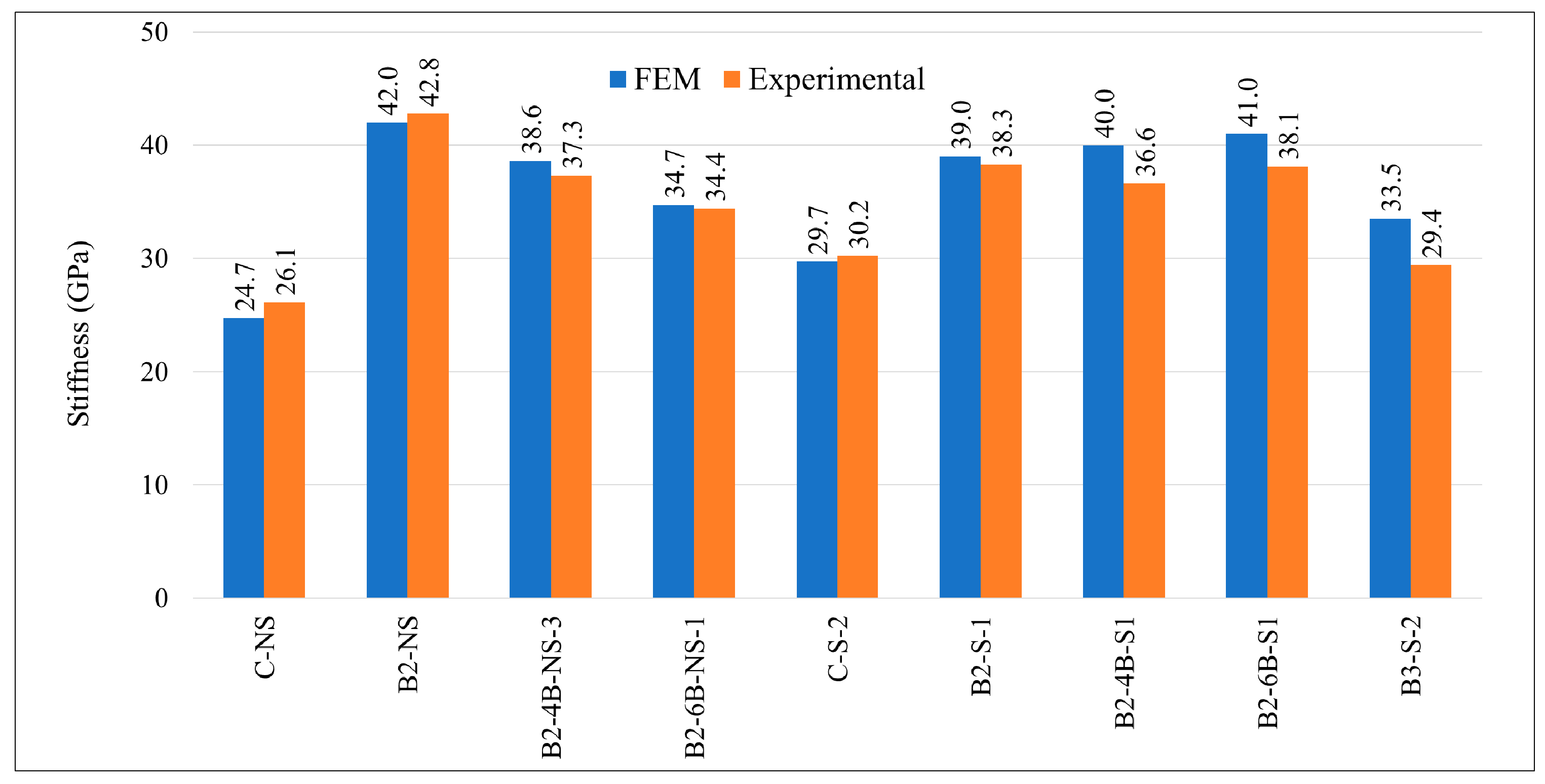
- In all experiments conducted on RC beams under impact loading (Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 and Figure 13), the beams failed in shear as opposed to flexure. Thus, there is a correlation between the application of fabric GFRP and the increased shear strength capacity of RC beams. The RC beams strengthened by fabric GFRP depicted a higher load-carrying capacity in both quasi-static and impact loadings compared to that of non-strengthened RC beams (Figure 7, Figure 9, Figure 12, and Figure 13). Fabric GFRP effectively increased the beam’s stiffness under both quasi-static and impact loadings (Figure 25).
- Although the beam’s stiffness under impact loading is increased as opposed to that under quasi-static loading, stiffness under impact loading will be reduced by increasing impact velocity (Figure 25).
- Sprayed GFRP (with and without through-bolts) increases the beam’s stiffness (Figure 26). The through-bolts are more effective in increasing the beam’s stiffness when some steel stirrups are present.
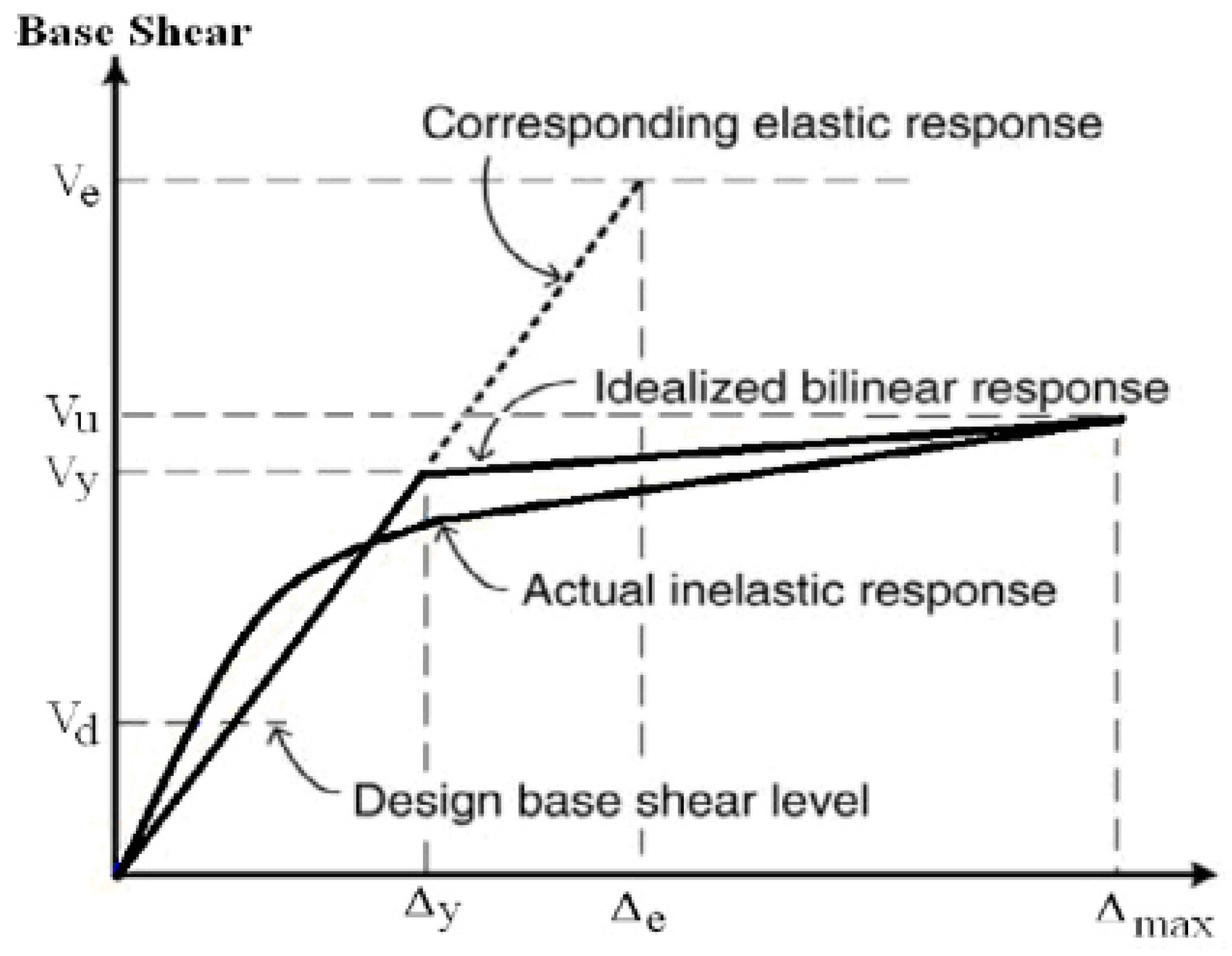
- Using FEM to predict the stiffness of RC beams was more effective for beams tested under quasi-static conditions as compared to those tested under impact loading.
Author Contributions
Funding
Conflicts of Interest
References
- Abrams, D.A. Effects of rate of application of load on the compressive strength of concrete. In Proceedings of the American Society for Testing and Materials, Atlantic City, NJ, USA, 26–29 June 1917; Volume 17, Part II. pp. 364–377. [Google Scholar]
- Atchley, B.L.; Furr, H.L. Strength and energy absorption capabilities of plain concrete under dynamic and static loadings. Am. Concr. Inst. J. 1967, 64, 745–756. [Google Scholar]
- Scott, B.D.; Park, R.; Priestley, M.J.N. Stress-strain behaviour of concrete confined by overlapping hoops at low and high strain rates. J. Am. Concr. Inst. 1982, 79, 496–498. [Google Scholar]
- Dilger, W.; Kand, R.; Kowalczyk, R. Ductility of plain and confined concrete under different strain rates. Am. Concr. Inst. J. 1984, 81, 73–81. [Google Scholar]
- Mlakar, P.F.; Vitaya-Udom, K.P.; Cole, R.A. Dynamic tensile-compressive behaviour of concrete. Am. Concr. Inst. J. 1986, 86, 484–491. [Google Scholar]
- Soroushian, P.; Choi, K.-B.; Alhamad, A. Dynamic constitutive behaviour of concrete. Am. Concr. Inst. J. 1986, 83, 251–259. [Google Scholar]
- Watstein, D. Effect of straining rate on the compressive strength and elastic properties of concrete. Am. Concr. Inst. J. 1953, 24, 729–744. [Google Scholar]
- Malvar, L.J.; Ross, C.A. Review of strain rate effects for concrete in tension. Mater. J. 1998, 95, 735–739. [Google Scholar]
- Bertero, V.V.; Rea, D.; Mahin, S.; Atalay, M.B. Rate of loading effects on uncracked and repaired reinforced concrete members. In Proceedings of the 5th World Conference on Earthquake Engineering, Rome, Italy, 25–29 June 1973; Volume II, pp. 1461–1470. [Google Scholar]
- Wakabayashi, M.; Nakamura, T.; Yoshida, N.; Iwai, S.; Watanabe, Y. Dynamic loading effects on the structural performance of concrete and steel materials and beams. In Proceedings of the 7th World Conference on Earthquake Engineering, Istanbul, Turkey, 8–13 September 1980. [Google Scholar]
- Fujikake, K.; Li, B.; Soeun, S. Impact response of reinforced concrete beam and its analytical evaluation. J. Struct. Eng. 2009, 135, 938–950. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, H. Prediction of the impact force on RC beams from a drop weight. Adv. Struct. Eng. 2016. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, Y.; Hao, H. Sensitivity of impact behavior of RC beams to contact stiffness. Int. J. Impact Eng. 2017. [Google Scholar] [CrossRef]
- Jabr, A.; El-Ragaby, A.; Ghrib, F. Effect of the fiber type and axial stiffness of FRCM on the flexural strengthening of RC beams. Fibers 2017, 5, 2. [Google Scholar] [CrossRef]
- Peng, H.; Shang, S.; Jin, Y.-J.; Wang, M. Experimental study of reinforced concrete beam with prestressed CFRP plate. Eng. Mech. 2008, 25, 142–151. [Google Scholar]
- White, T.; Soudki, K.; Erki, M. Response of RC beams strengthened with CFRP laminates and subjected to a high rate of loading. J. Compos. Constr. 2001, 5, 153–162. [Google Scholar] [CrossRef]
- Tang, T.; Saadatmanesh, H. Behavior of concrete beams strengthened with fiber-reinforced polymer laminates under impact loading. J. Compos. Constr. 2003, 7, 209–218. [Google Scholar] [CrossRef]
- Tang, T.; Saadatmanesh, H. Analytical and experimental studies of fiber-reinforced polymer strengthened concrete beams under impact loading. ACI Struct. J. 2005, 102, 139–149. [Google Scholar]
- Hamed, E.; Rabinovitch, O. Dynamic behavior of reinforced concrete beams strengthened with composite materials. J. Compos. Constr. 2005, 9, 429–440. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, H. Impact behavior of FRP-strengthened RC beams without stirrups. J. Compos. Constr. 2016. [Google Scholar] [CrossRef]
- Meola, C.; Boccardi, S.; Carlomagno, G.M. Infrared thermography for inline monitoring of glass/epoxy under impact and quasi-static bending. Appl. Sci. 2018, 8, 301. [Google Scholar] [CrossRef]
- Soleimani, S.M. Sprayed Glass Fiber Reinforced Polymers in Shear Strengthening and Enhancement of Impact Resistance of Reinforced Concrete Beams. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 2007. [Google Scholar]
- Soleimani, S.M.; Banthia, N. A novel drop weight impact setup for testing reinforced concrete beams. J. Exp. Tech. 2014, 38, 72–79. [Google Scholar] [CrossRef]
- Soleimani, S.M.; Banthia, N. Reinforced concrete beams under impact loading and influence of a GFRP coating. Int. Rev. Civ. Eng. 2010, 1, 68–77. [Google Scholar]
- ABAQUS Analysis User’s Guide. Available online: http://dsk.ippt.pan.pl/docs/abaqus/v6.13/books/usb/default.htm (accessed on 16 July 2019).
- Sayyar Roudsari, S.; Hamoush, S.A.; Soleimani, S.M.; Madandoust, R. Evaluation of large-size reinforced concrete columns strengthened for axial load using fiber reinforced polymers. Eng. Struct. 2019, 178, 680–693. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Zaree, M. Determination the response modification factors of buckling restrained braced frames. Procedia Eng. 2013, 54, 222–231. [Google Scholar] [CrossRef]
- Tanarslan, M.; Alver, N.; Jahangiri, R.; Yalçınkaya, Ç.; Yazıcı, H. Flexural strengthening of RC beams using UHPFRC laminates: Bonding techniques and rebar addition. Constr. Build. Mater. 2017, 155, 45–55. [Google Scholar] [CrossRef]
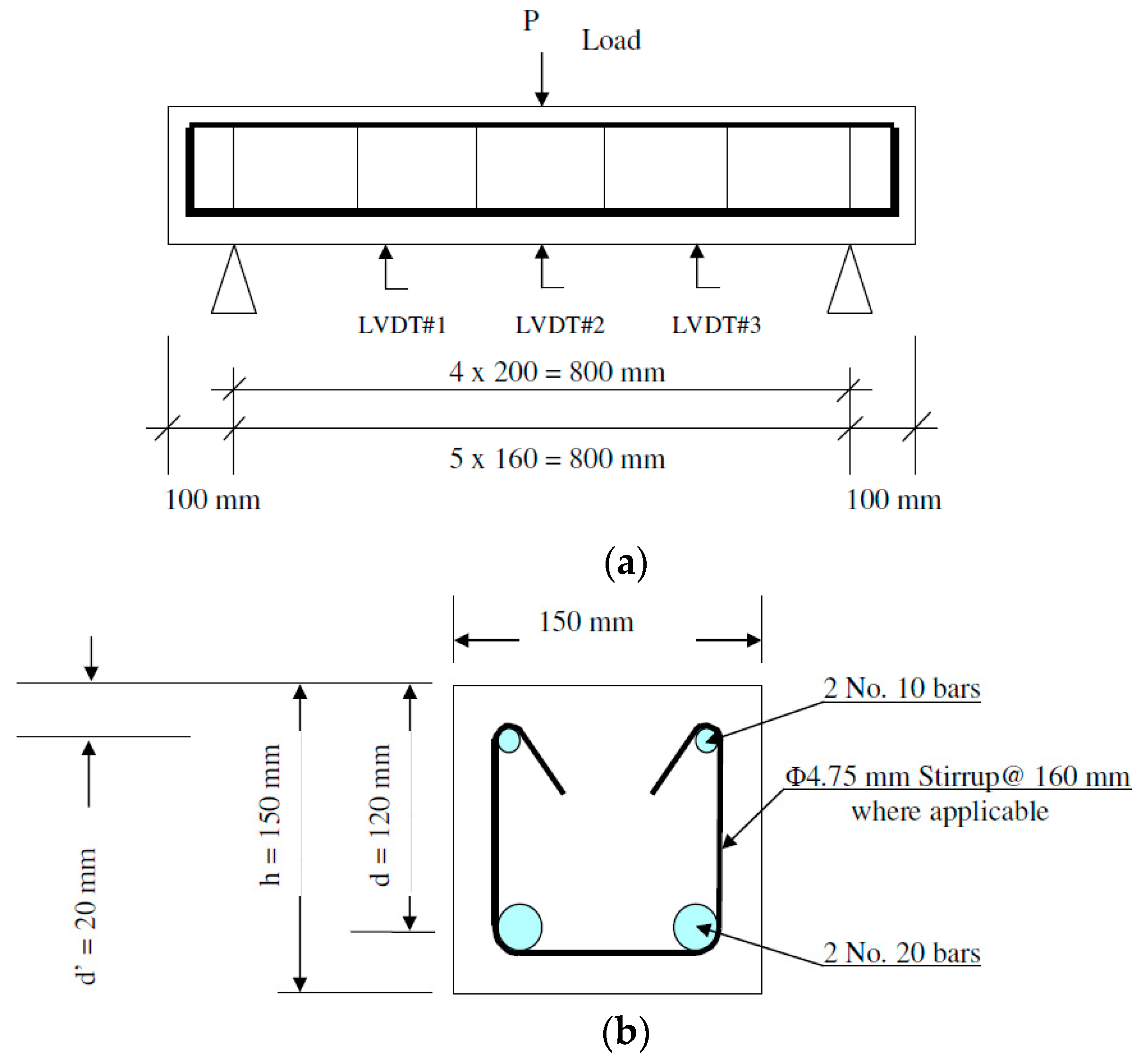

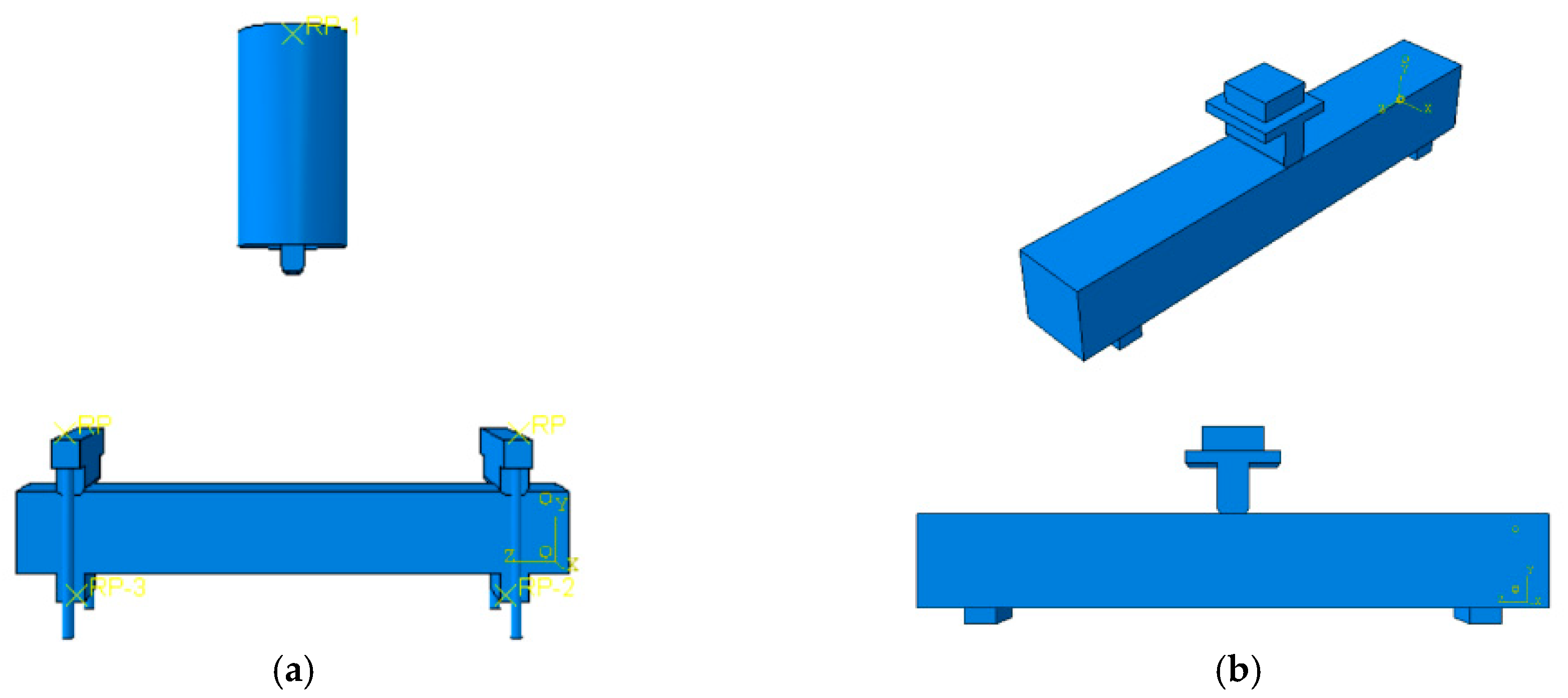








| Parameter | Definition | Value | Unit |
|---|---|---|---|
| f’c | Specified compressive strength of concrete | 44 | MPa |
| fy | Specified yield strength of tension reinforcement | M-10: 474; M-20: 440 | MPa |
| fys | Specified yield strength of shear reinforcement | 600 | MPa |
| fu | Specified ultimate strength of tension reinforcement | M-10: 720; M-20: 695 | MPa |
| fus | Specified ultimate strength of shear reinforcement | 622 | MPa |
| As | Area of reinforcement (M-10 and M-20 for tension and ϕ4.75 for shear) | M-10: 100; M-20: 300; ϕ4.75: 18.1 | mm2 |
| Properties | Value | Unit |
|---|---|---|
| Ultimate tensile strength | 69 | MPa |
| Tensile modulus | 14 | GPa |
| Ultimate rupture strain | 0.63 | % |
| Properties | Value | Unit |
|---|---|---|
| Ultimate tensile strength | 1517 | MPa |
| Tensile modulus | 72.4 | GPa |
| Ultimate tensile strength per unit width | 0.536 | KN/mm/ply |
| Tensile modulus per unit width | 25.6 | KN/mm/ply |
| Ultimate rupture strain | 2.1 | % |
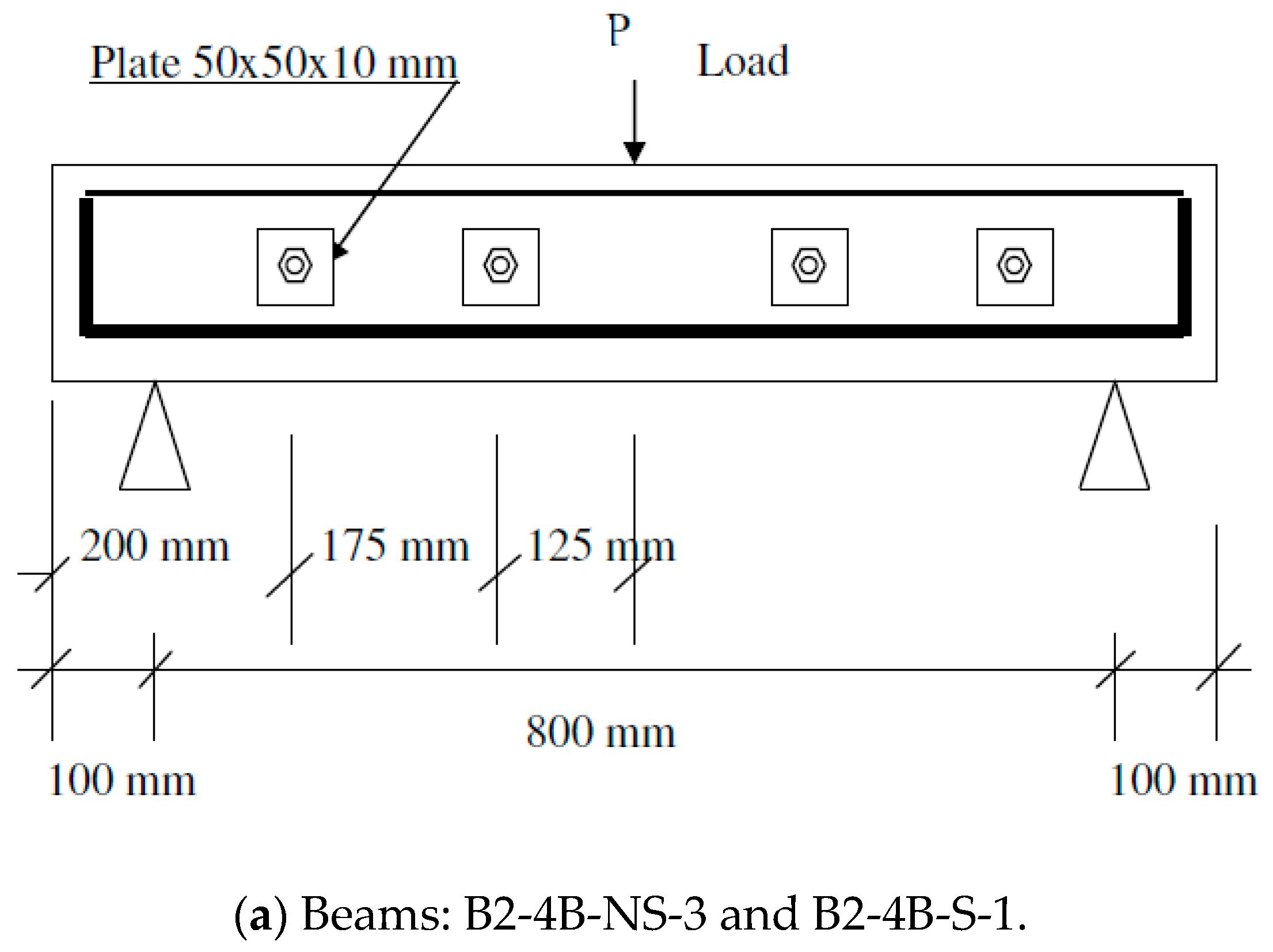
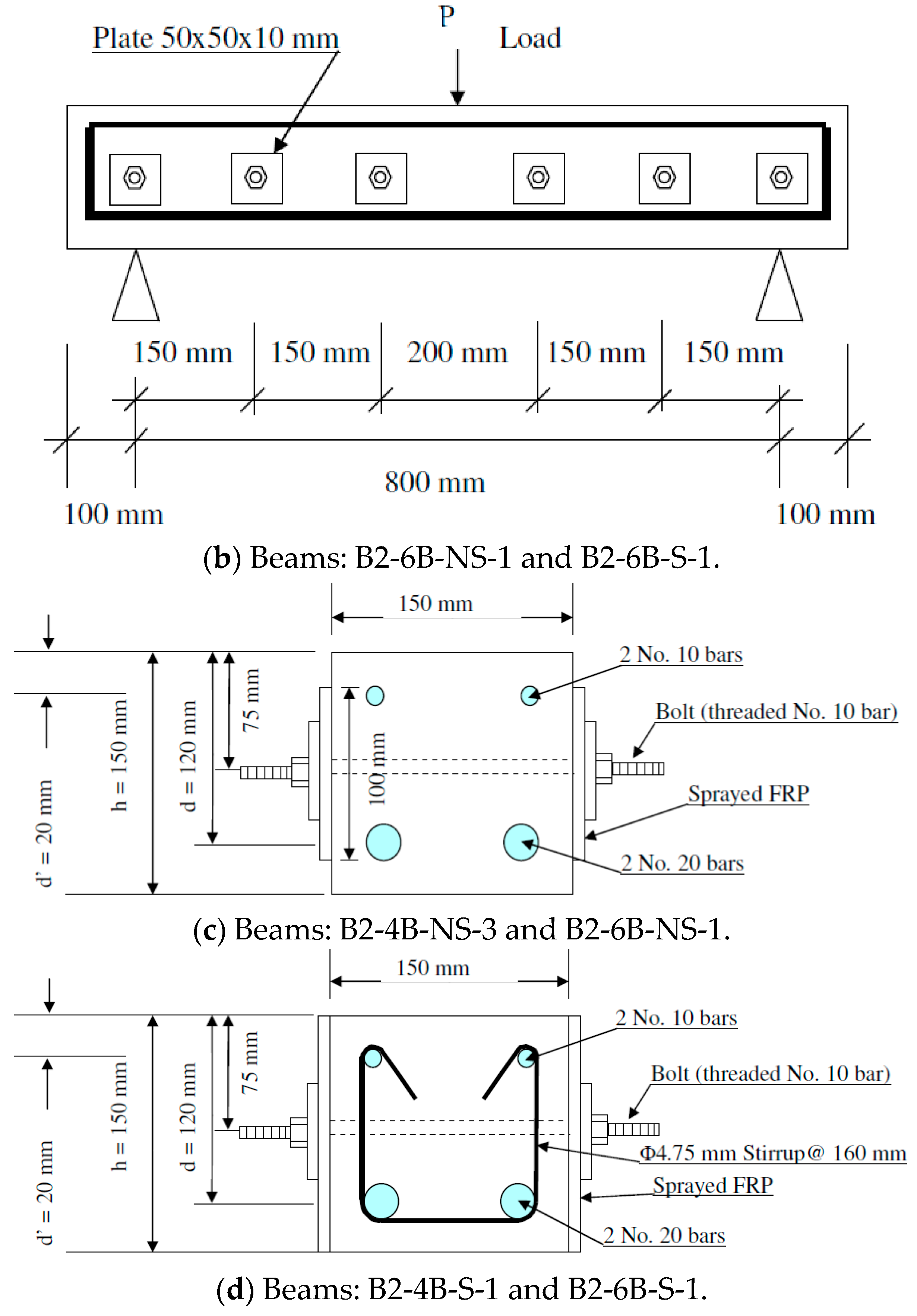
| Beam’s Designation | Stirrups? | Sprayed GFRP on Two Sides or Three? | Width of Sprayed GFRP on the Sides (mm) | Thickness of Sprayed GFRP (mm) | No. of Through Bolts as Mechanical Fastener |
|---|---|---|---|---|---|
| C-NS | No | N/A | N/A | N/A | N/A |
| B2-NS | No | 2 | 100 | 4 | N/A |
| B2-4B-NS-3 | No | 2 | 100 | 4 | 4 |
| B2-6B-NS-1 | No | 2 | 100 | 3.5 | 6 |
| C-S-2 | Yes | N/A | N/A | N/A | N/A |
| B2-S-1 | Yes | 2 | 150 | 3.5 | N/A |
| B2-4B-S-1 | Yes | 2 | 150 | 3.5 | 4 |
| B2-6B-S-1 | Yes | 2 | 150 | 4 | 6 |
| B3-S-2 | Yes | 3 | 150 | 4 | N/A |
| Beam’s Designation | Quasi-Static or Impact? | Drop Height (mm) | Impact Velocity (m/s) |
|---|---|---|---|
| BS | Quasi-static (control) | NA | NA |
| BI-400 | Impact | 400 | 2.8 |
| BI-500 | Impact | 500 | 3.13 |
| BI-600 | Impact | 600 | 3.43 |
| BI-1000 | Impact | 1000 | 4.43 |
| BI-2000 | Impact | 2000 | 6.26 |
| BS-GFRP | Quasi-static (control) | NA | NA |
| BI-600-GFRP | Impact | 600 | 3.43 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soleimani, S.M.; Sayyar Roudsari, S. Analytical Study of Reinforced Concrete Beams Tested under Quasi-Static and Impact Loadings. Appl. Sci. 2019, 9, 2838. https://doi.org/10.3390/app9142838
Soleimani SM, Sayyar Roudsari S. Analytical Study of Reinforced Concrete Beams Tested under Quasi-Static and Impact Loadings. Applied Sciences. 2019; 9(14):2838. https://doi.org/10.3390/app9142838
Chicago/Turabian StyleSoleimani, Sayed Mohamad, and Sajjad Sayyar Roudsari. 2019. "Analytical Study of Reinforced Concrete Beams Tested under Quasi-Static and Impact Loadings" Applied Sciences 9, no. 14: 2838. https://doi.org/10.3390/app9142838
APA StyleSoleimani, S. M., & Sayyar Roudsari, S. (2019). Analytical Study of Reinforced Concrete Beams Tested under Quasi-Static and Impact Loadings. Applied Sciences, 9(14), 2838. https://doi.org/10.3390/app9142838




