Reversible Data Hiding Scheme in Homomorphic Encrypted Image Based on EC-EG
Abstract
1. Introduction
2. Related Knowledge
2.1. Elliptic Curve
- 1.
- 2.
- 3.
- 4.
- (addition rule)If is satisfied when , then
- 5.
- (multiple point rule) , If is satisfied, then
2.2. Elliptic Curve Public Key Cryptography
- p is of course larger and safer, but the larger is p, the slower is the calculation speed. p is about 200 bits to meet general safety requirements:
- ;
- ;
- ;
- n is a prime number; and
- .
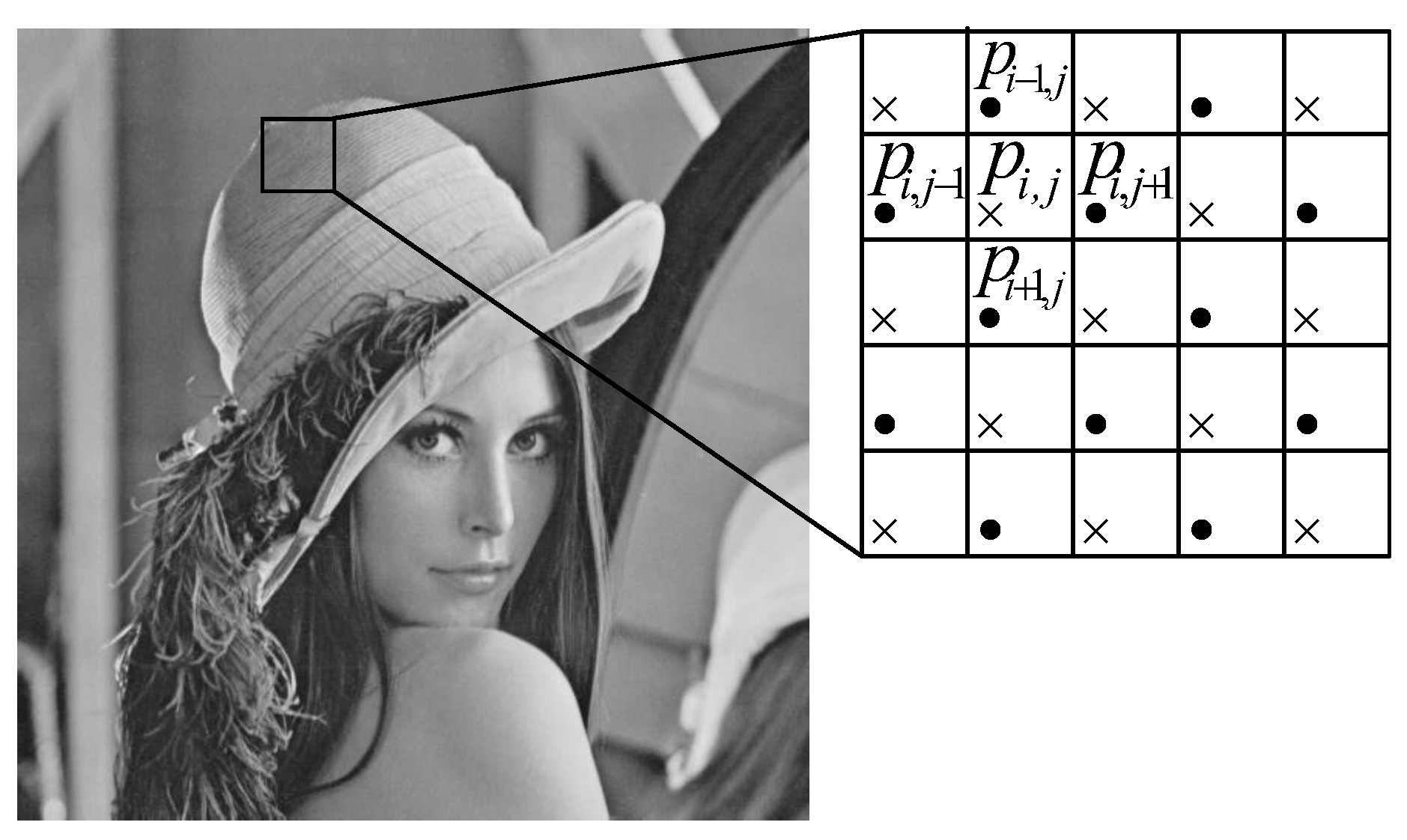
2.3. Rhombus Pattern Based PEE
2.3.1. The Embedding Procedure
2.3.2. Overflow or Underflow Processing
2.3.3. Extraction and Recovery Procedures
3. Proposed Scheme
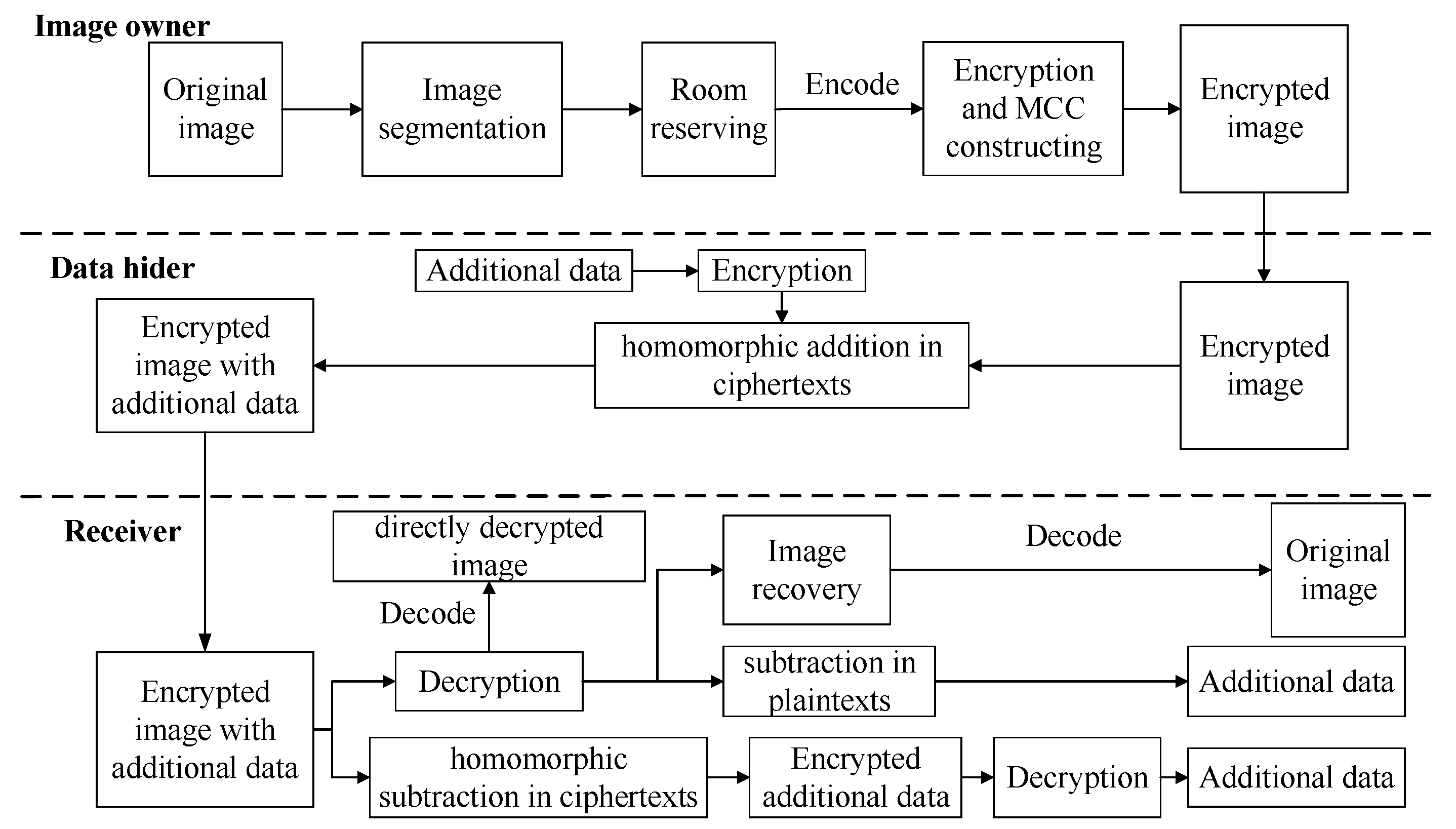
3.1. Overall Framework of the Proposed Scheme
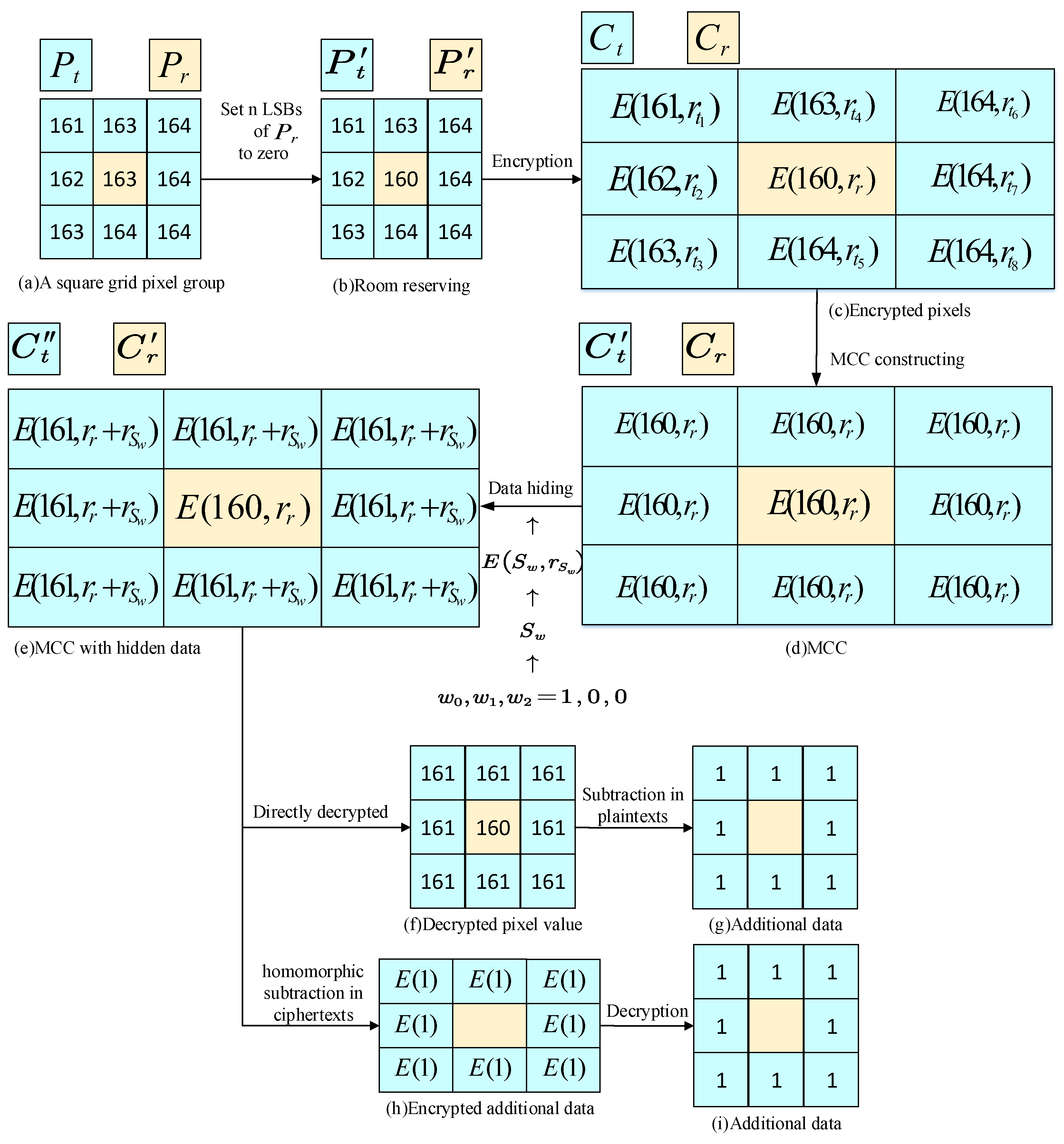
3.2. Room Reserving
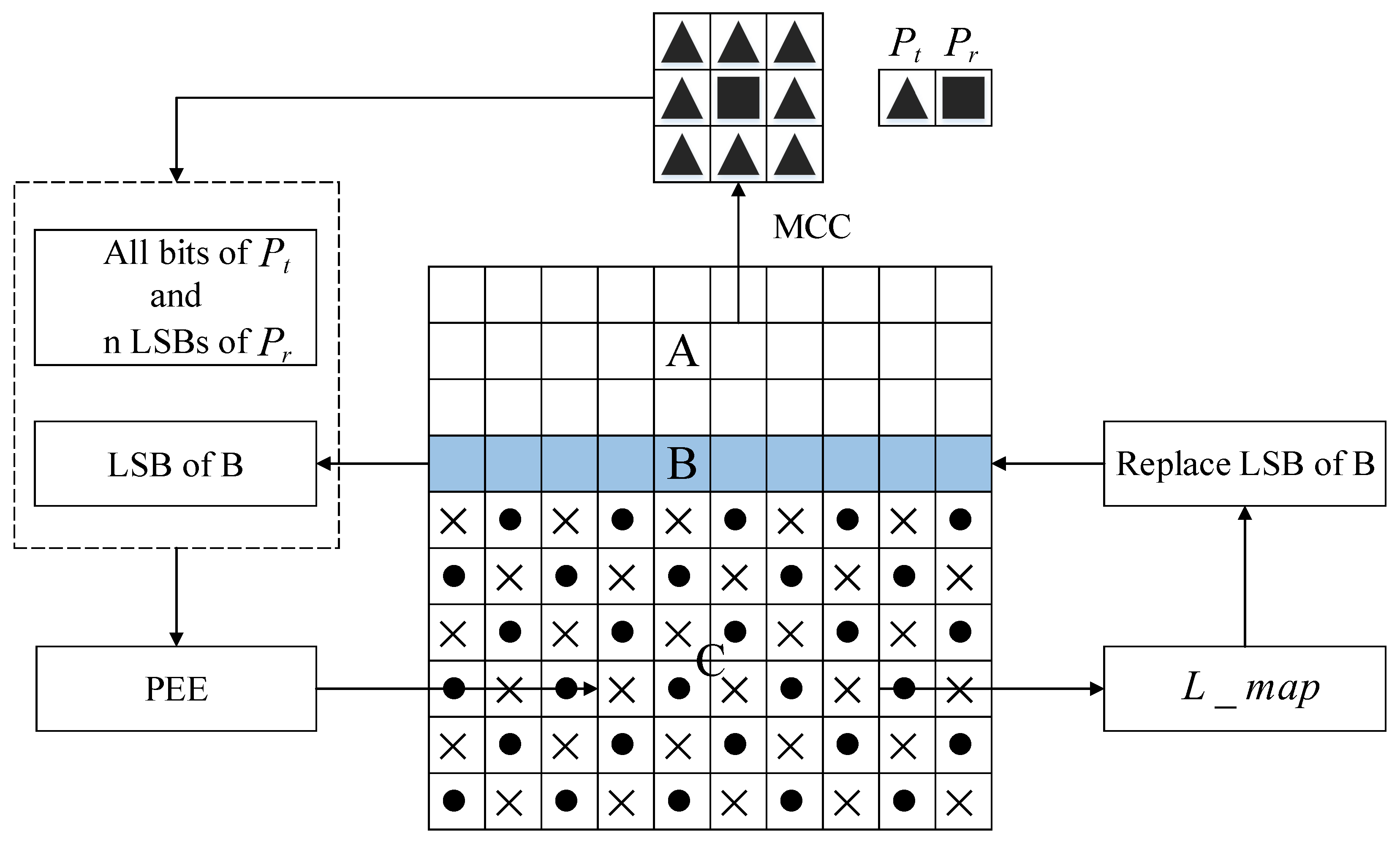
3.2.1. Image Partition
3.2.2. Self-Reversible Embedding
3.2.3. Vacating Room
3.3. Image Encryption
3.4. Construction of Mirroring Central Ciphertext
3.5. Data Hiding
3.6. Data Extraction
3.6.1. Extract the Embedded Data from Encrypted Image
3.6.2. Extract the Embedded Data from Decrypted Image
3.7. Image Restoration
4. Simulation Experiment and Theoretical Analysis
4.1. Analysis of Embedded Capacity and PSNR
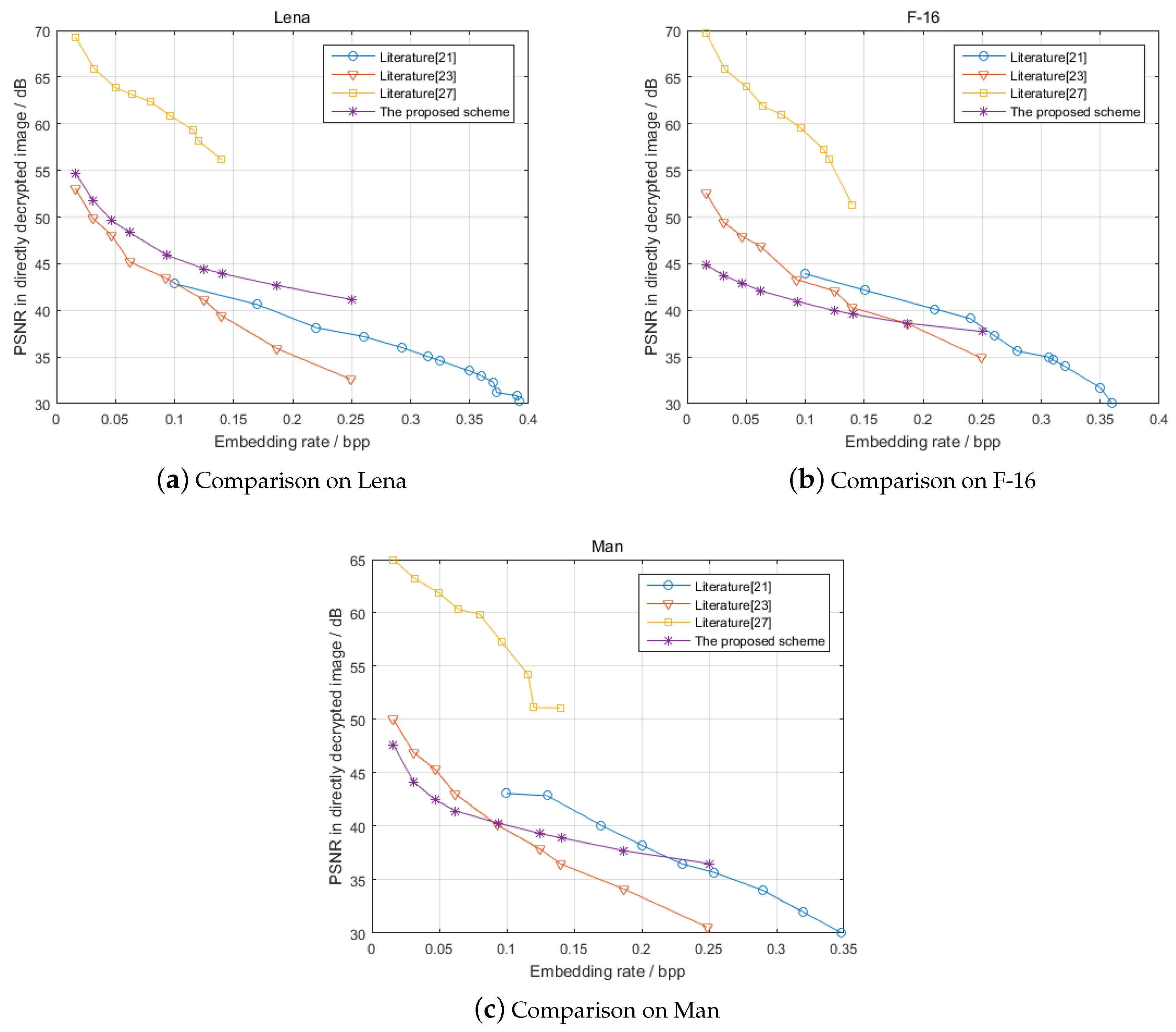
4.2. Performance Comparison
4.3. Analysis of Security
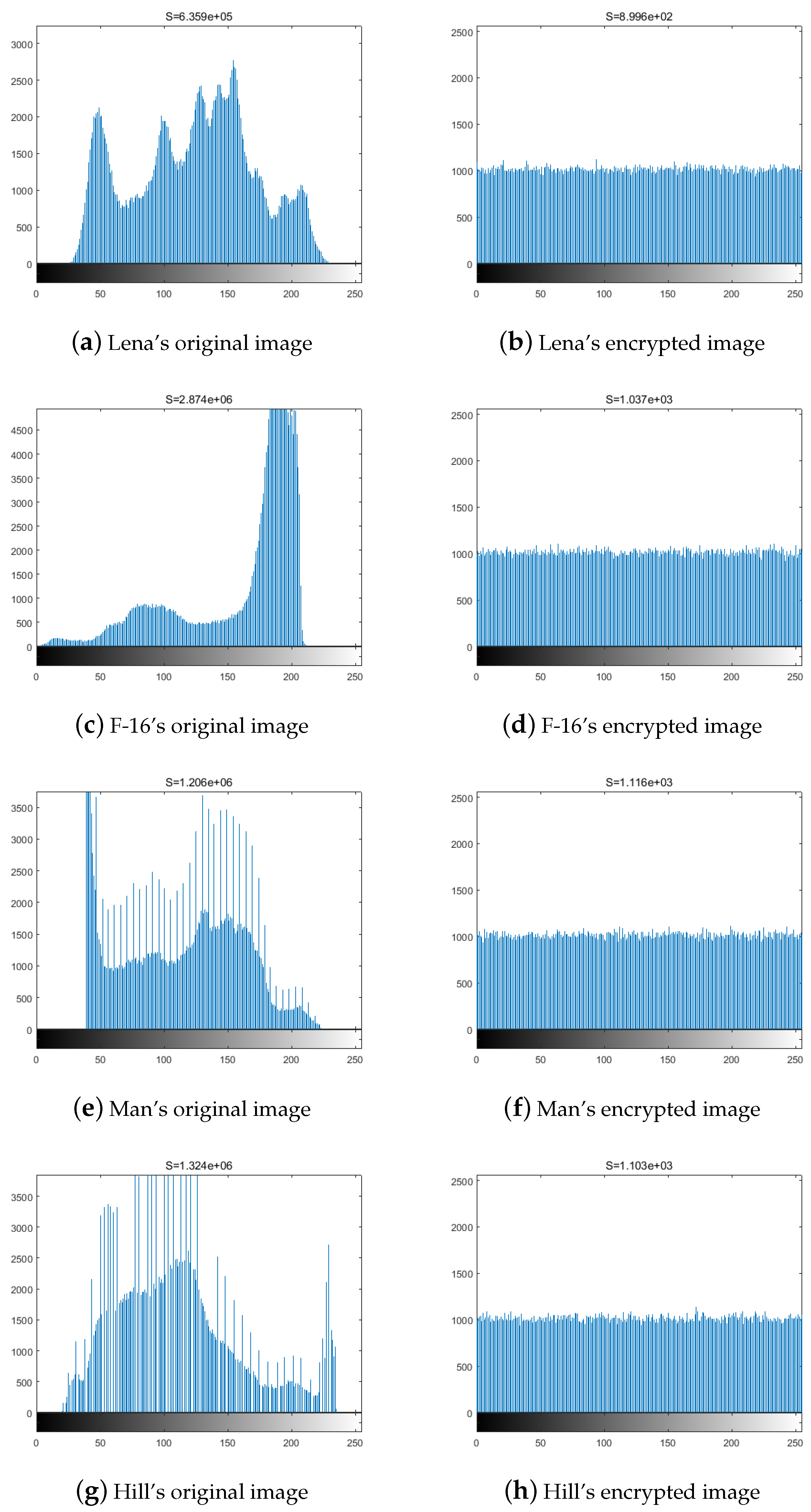
4.3.1. Histogram Analysis of Encrypted Image
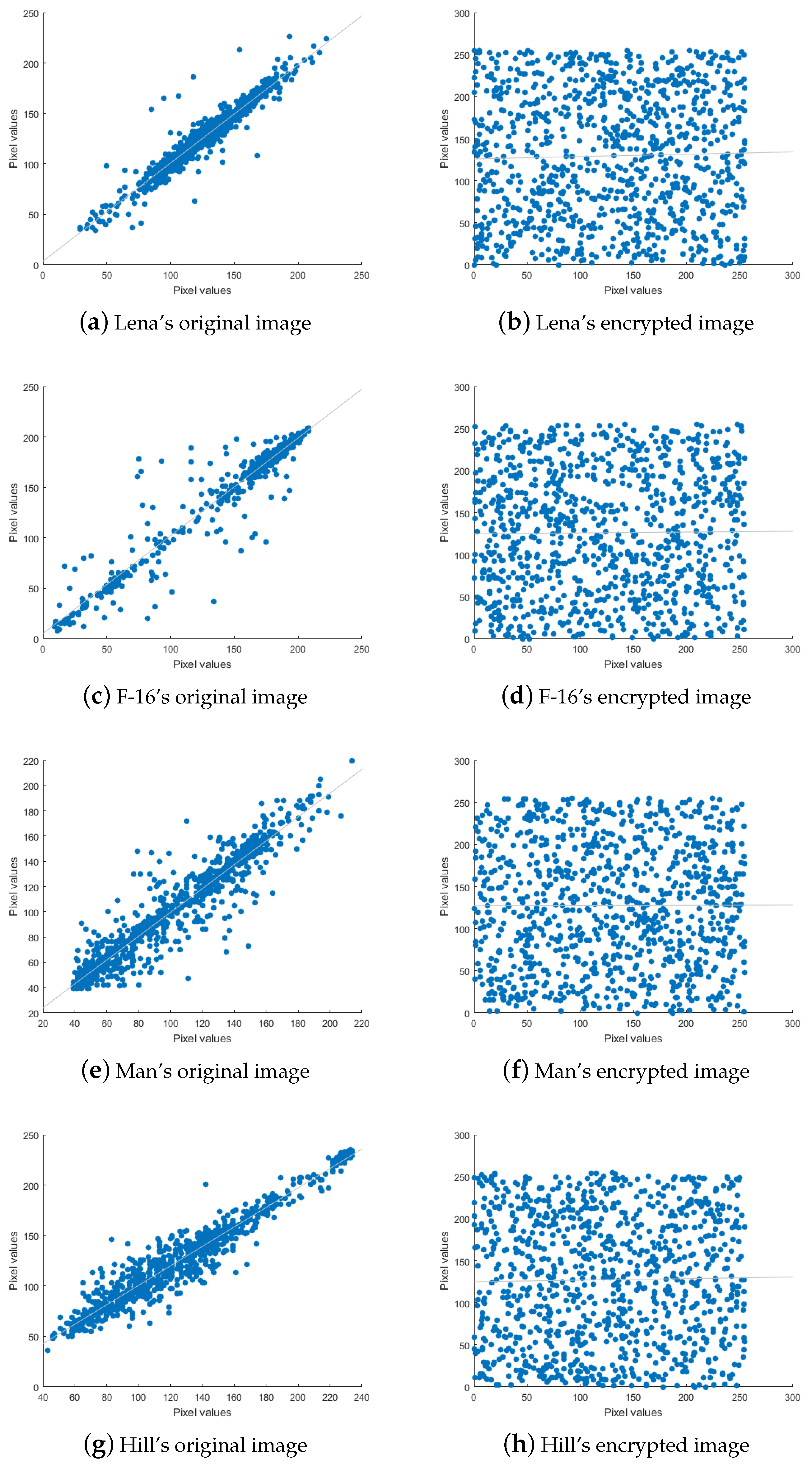
4.3.2. Correlation Analysis of Adjacent Pixels
4.3.3. Information Entropy Analysis
5. Conclusions
- A novel method of reversible data hiding in homomorphic encrypted image based on EC-EG is proposed.
- By constructing MCC, the embedded capacity is improved.
- By performing histogram analysis of encrypted image, correlation analysis of adjacent pixels and information entropy analysis, we proved the statistical security of the encryption scheme in this paper.
- However, the method of vacating room before encryption increases the risk of plaintext leakage. Therefore, it should be improved in the future to be a reversible data hiding scheme in homomorphic encrypted image that does not require preprocessing of plaintext.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abdallah, E.E.; Hamza, A.B.; Bhattacharya, P. MPEG video watermarking using tensor singular value decomposition. In Image Analysis & Recognition, Proceedings of the International Conference, ICIAR, Montreal, QC, Canada, 22–24 August 2007; Springer: Berlin, Germany, 2007. [Google Scholar] [CrossRef]
- Abdallah, E.E.; Hamza, A.B.; Bhattacharya, P. Video watermarking using wavelet transform and tensor algebra. Signal Image Video Process. 2010, 4, 233–245. [Google Scholar] [CrossRef]
- Yu, X.Y.; Wang, C.Y.; Zhou, X. A survey on robust video watermarking algorithms for copyright protection. Appl. Sci. 2018, 8, 1891. [Google Scholar] [CrossRef]
- Ke, Y.; Zhang, M.Q.; Su, T.T. A novel multiple bits reversible data hiding in encrypted domain based on R-LWE. J. Comput. Res. Dev. 2016, 53, 2307–2322. [Google Scholar]
- BARTON. Method and Apparatus for Embedding Authentication Information within Digital Data. U.S. Patent 5646997, 8 July 1997.
- Fridrich, J.; Goljan, M.; Du, R. Lossless data embedding-new paradigm in digital watermarking. Eur. Assoc. Signal Process 2002, 2002, 185–196. [Google Scholar] [CrossRef]
- Celik, M.; Sharma, G.; Tekalp, A. Lossless generalized–LSB data embedding. IEEE Trans. Image Process. 2005, 14, 253–266. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Sachnev, V.; Shi, Y.Q. A novel difference expansion transform for reversible data embedding. IEEE Trans. Inf. Forensics Secur. 2008, 4, 456–465. [Google Scholar]
- Thodi, D.M.; Rodriguez, J.J. Expansion embedding techniques for reversible watermarking. IEEE Trans. Image Process 2007, 16, 721–730. [Google Scholar] [CrossRef]
- Ni, Z.; Shi, Y.Q.; Ansari, N.; Su, W. Reversible data hiding. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 354–362. [Google Scholar]
- Lee, S.K.; Suh, Y.H.; Ho, Y.S. Reversible image authentication based on watermarking. In Proceedings of the 2006 IEEE International Conference on Multimedia and Expo, Toronto, ON, Canada, 9–12 July 2006; pp. 1321–1324. [Google Scholar]
- Zhang, X.P. Reversible data hiding in encrypted image. IEEE Signal Process. Lett. 2011, 18, 255–258. [Google Scholar] [CrossRef]
- Hong, W.; Chen, T.S.; Wu, H.Y. An improved reversible data hiding in encrypted images using side match. IEEE Signal Process. Lett. 2012, 19, 199–202. [Google Scholar] [CrossRef]
- Hong, W.; Chen, T.S.; Chen, J. Reversible data embedment for encrypted cartoon images using unbalanced bit flipping. In International Conference in Swarm Intelligence; Springer: London, UK, 2013; pp. 208–214. [Google Scholar]
- Zhang, X.P. Separable reversible data hiding in encrypted image. IEEE Trans. Inf. Forensics Secur. 2012, 7, 826–832. [Google Scholar] [CrossRef]
- Ma, K.D.; Zhang, W.M.; Zhao, X.F. Reversible data hiding in encrypted images by reserving room before encryption. IEEE Trans. Inf. Forensics Secur. 2013, 8, 553–562. [Google Scholar] [CrossRef]
- Zhang, W.M.; Ma, K.D.; Yu, N.H. Reversibility improved data hiding in encrypted images. Signal Process. 2014, 94, 118–127. [Google Scholar] [CrossRef]
- Chen, Y.C.; Shiu, C.W.; Horng, G. Encrypted signal-based reversible data hiding with public key cryptosystem. J. Vis. Commun. Image Represent. 2014, 25, 1164–1170. [Google Scholar] [CrossRef]
- Shiu, C.W.; Chen, Y.C.; Hong, W. Encrypted image-based reversible data hiding with public key cryptography from difference expansion. Signal Process. Image Commun. 2015, 39, 226–233. [Google Scholar] [CrossRef]
- Wu, X.T.; Chen, B.; Weng, J. Reversible data hiding for encrypted signals by homomorphic encryption and signal energy transfer. J. Vis. Commun. Image Represent. 2016, 41, 58–64. [Google Scholar] [CrossRef]
- Zhang, X.P.; Long, J.; Wang, Z.C. Lossless and reversible data hiding in encrypted images with public-key cryptography. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 1622–1631. [Google Scholar] [CrossRef]
- Fridrich, J.; Goljan, M.; Lisonek, P. Writing on wet paper. IEEE Trans. Signal Process. 2005, 53, 3923–3935. [Google Scholar] [CrossRef]
- Xiang, S.J.; Luo, X.R. Reversible data hiding in homomorphic encrypted domain by mirroring ciphertext group. IEEE Trans. Circuits Syst. Video Technol. 2017, 10, 1051–1062. [Google Scholar] [CrossRef]
- Zhou, N.; Wang, H.; Liu, M.M. Reversible data hiding algorithm in homomorphic encrypted domain based on EC-EG. In Intelligent Networking and Collaborative Systems; Springer: Berlin, Germany, 2019. [Google Scholar]
- Sachnev, V.; Kim, H.J.; Nam, J. Reversible watermarking algorithm using sorting and prediction. IEEE Trans. Circuits Syst. Video Technol. 2009, 19, 989–999. [Google Scholar] [CrossRef]
- Tian, J. Reversible data embedding using a difference expansion. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 890–896. [Google Scholar] [CrossRef]
- Li, Z.X.; Dong, D.P.; Xia, Z.H. High-capacity reversible data hiding for encrypted multimedia data with somewhat homomorphic encryption. IEEE Access 2018, 6, 60635–60644. [Google Scholar]
- Sun, X.H. Image Encryption Algorithms and Practices with Implementations in C#; Science Press: Beijing, China, 2013. [Google Scholar]

| Embedding Capacity (bits) | PSNR (dB) | ||||
|---|---|---|---|---|---|
| n = 1 | n = 2 | n = 3 | n = 4 | ||
| Lena | 4095 | 51.681 | 53.448 | 54.719 | 45.353 |
| 8190 | 48.765 | 51.13 | 51.786 | 43.472 | |
| 12,285 | 46.993 | 49.022 | 49.618 | 41.04 | |
| 16,380 | 45.658 | 48.012 | 48.32 | 40.132 | |
| 24,570 | 43.034 | 45.684 | 45.885 | 37.97 | |
| 32,760 | 40.82 | 44.301 | 44.456 | 36.384 | |
| 36,855 | 39.983 | 43.634 | 43.92 | 35.609 | |
| 49,140 | 38.219 | 42.09 | 42.667 | 34.353 | |
| 65,520 | 35.829 | 40.03 | 41.146 | 32.611 | |
| Embedding Capacity (bits) | PSNR (dB) | |||
|---|---|---|---|---|
| Lena | F-16 | Man | Hill | |
| 4095 | 54.719 | 44.913 | 47.637 | 54.526 |
| 8190 | 51.786 | 43.715 | 44.158 | 50.866 |
| 12,285 | 49.618 | 42.896 | 42.486 | 48.695 |
| 16,380 | 48.32 | 42.12 | 41.422 | 46.843 |
| 24,570 | 45.885 | 40.956 | 40.277 | 44.61 |
| 32,760 | 44.456 | 39.956 | 39.31 | 42.919 |
| 36,855 | 43.92 | 39.574 | 38.897 | 42.353 |
| 49,140 | 42.667 | 38.599 | 37.73 | 40.561 |
| 65,520 | 41.146 | 37.727 | 36.527 | 39.135 |
| Image | (bits) |
|---|---|
| Lena | 33 |
| F-16 | 670 |
| Man | 755 |
| Hill | 128 |
| Literature | Features | ||
|---|---|---|---|
| Separable | Computational Complexity of Data Hiding | Protection Mechanism of the Hidden Data | |
| Method in [21] | Yes | WPC mechanism | |
| Homomorphic and probabilistic | |||
| Method in [23] | Yes | Mechanism of Paillier | |
| Method in [27] | Yes | SHE(R-LWE-based) | |
| Homomorphic Mechanism | |||
| The proposed scheme | Yes | of EC-EG | |
| Image | Adjacent Pixel Correlation Coefficients | ||
|---|---|---|---|
| Horizontal | Vertical | Diagonal | |
| (a) Original image | 0.962 | 0.975 | 0.947 |
| 0.972 | 0.974 | 0.942 | |
| 0.959 | 0.972 | 0.94 | |
| 0.96 | 0.98 | 0.941 | |
| (b) Encrypted image | 0.056 | −0.041 | −0.012 |
| −0.019 | −0.034 | −0.089 | |
| −0.05 | −0.006 | 0.02 | |
| −0.009 | −0.042 | 0.023 | |
| Image | Information Entropy | |
|---|---|---|
| Cover Image | Encrypted Image | |
| Lena | 7.445 075 | 7.999 386 |
| F-16 | 6.705 888 | 7.999 290 |
| Man | 7.192 588 | 7.999 236 |
| Hill | 7.094 869 | 7.999 246 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, N.; Zhang, M.; Wang, H.; Liu, M.; Ke, Y.; Wang, X.A. Reversible Data Hiding Scheme in Homomorphic Encrypted Image Based on EC-EG. Appl. Sci. 2019, 9, 2910. https://doi.org/10.3390/app9142910
Zhou N, Zhang M, Wang H, Liu M, Ke Y, Wang XA. Reversible Data Hiding Scheme in Homomorphic Encrypted Image Based on EC-EG. Applied Sciences. 2019; 9(14):2910. https://doi.org/10.3390/app9142910
Chicago/Turabian StyleZhou, Neng, Minqing Zhang, Han Wang, Mengmeng Liu, Yan Ke, and Xu An Wang. 2019. "Reversible Data Hiding Scheme in Homomorphic Encrypted Image Based on EC-EG" Applied Sciences 9, no. 14: 2910. https://doi.org/10.3390/app9142910
APA StyleZhou, N., Zhang, M., Wang, H., Liu, M., Ke, Y., & Wang, X. A. (2019). Reversible Data Hiding Scheme in Homomorphic Encrypted Image Based on EC-EG. Applied Sciences, 9(14), 2910. https://doi.org/10.3390/app9142910






