Study on the Design and Cutting Performance of a Revolving Cycloid Milling Cutter
Abstract
:Featured Application
Abstract
1. Introduction
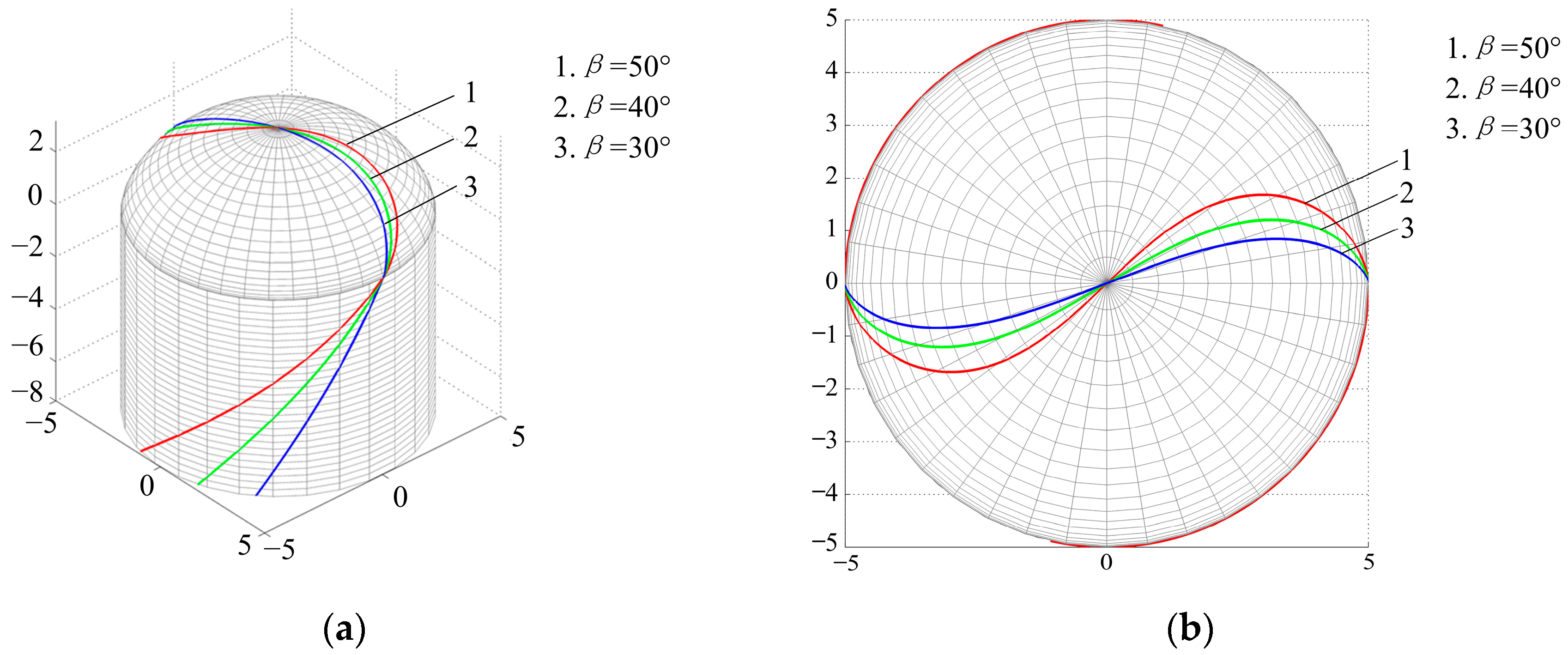
2. Design of the Revolving Cycloid Milling Cutter
2.1. Establishment and Simulation of Geometric Model for the Revolving Cycloid Milling Cutter
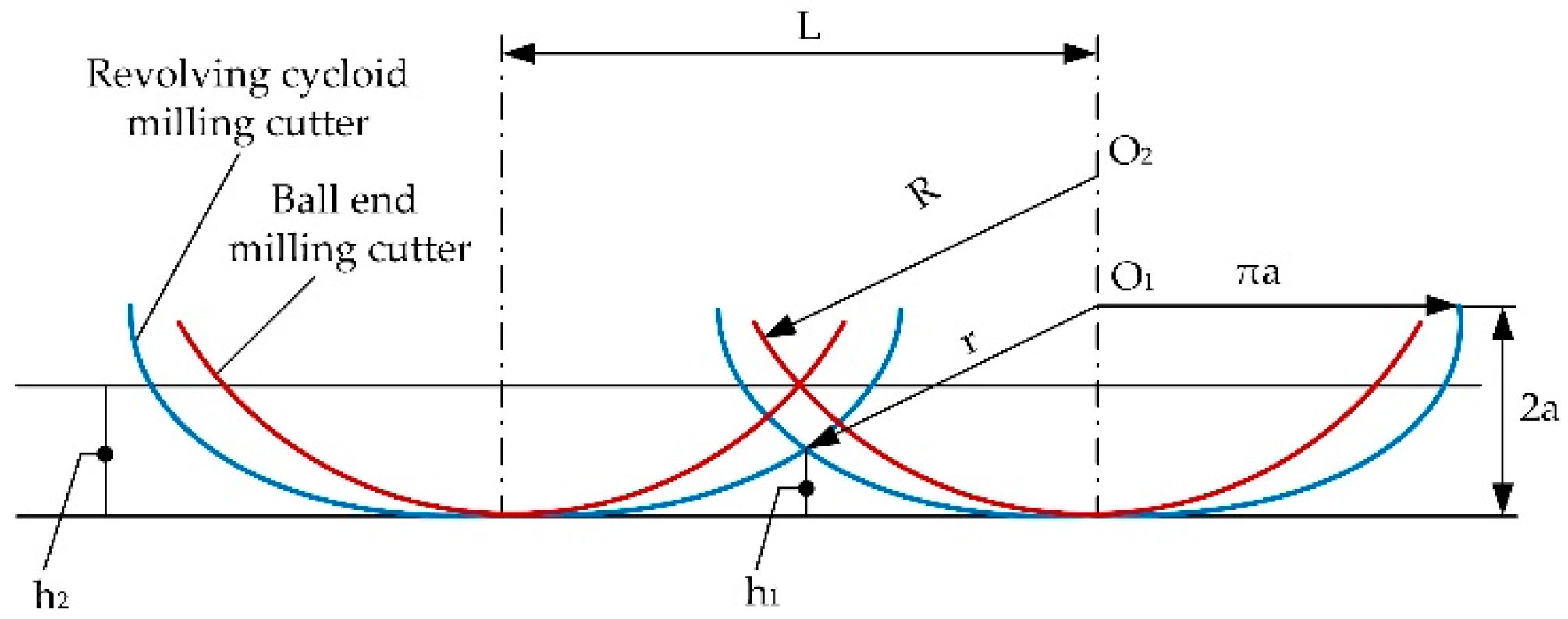
2.2. Comparison of Cutting States of the Revolving Cycloid Milling Cutter and the Ball-end Milling Cutter
3. Fabrications and Detection of the Revolving Cycloid Milling Cutter
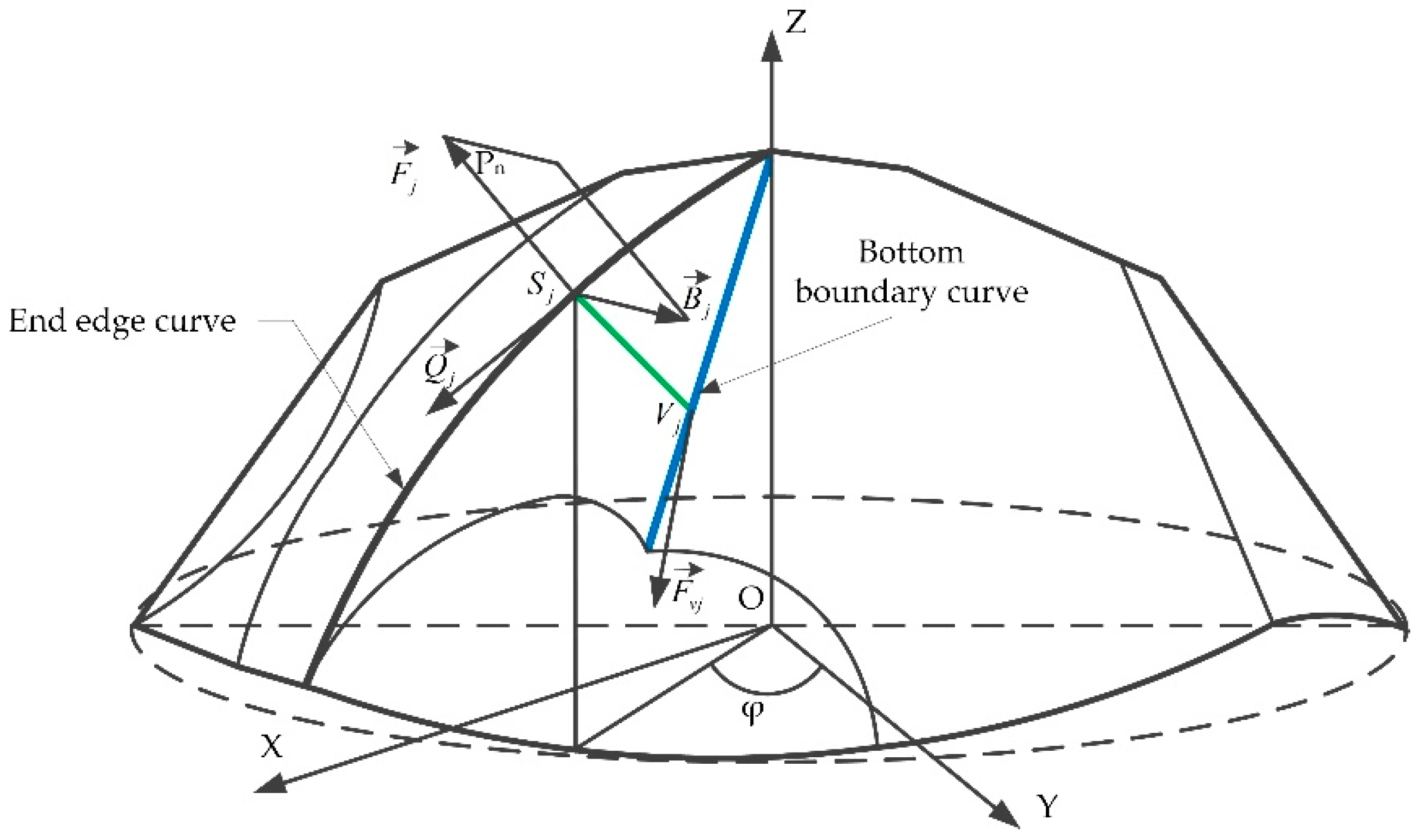
3.1. Establishment of the Grinding Model for the Rake Face of the Revolving Cycloid Milling Cutter
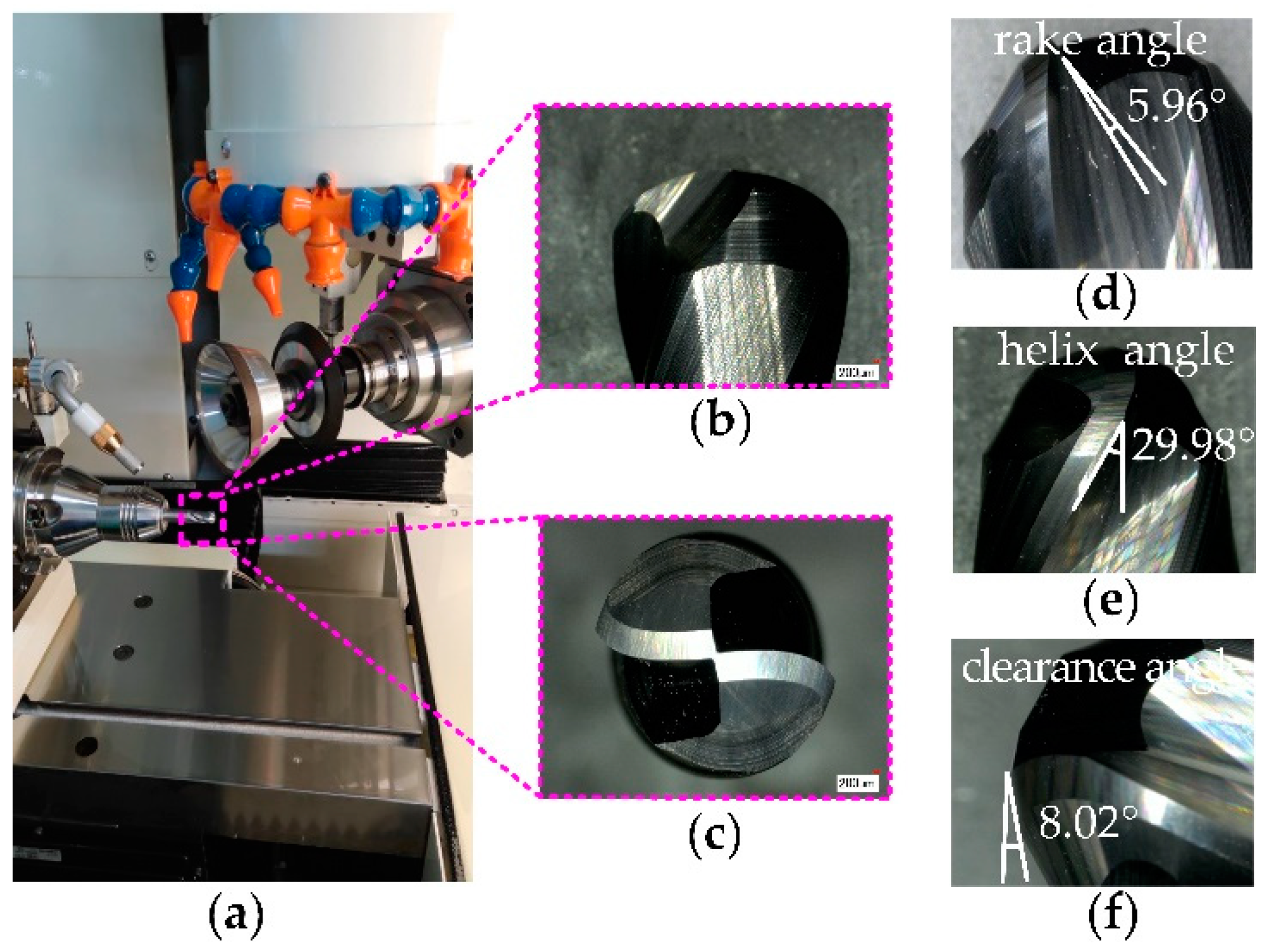
3.2. Study on the Fabrication and Testing of the Revolving Cycloid Milling Cutter
4. Study on the Cutting Performance of the Revolving Cycloid Milling Cutter
4.1. Test Conditions
4.2. Results and Discussion
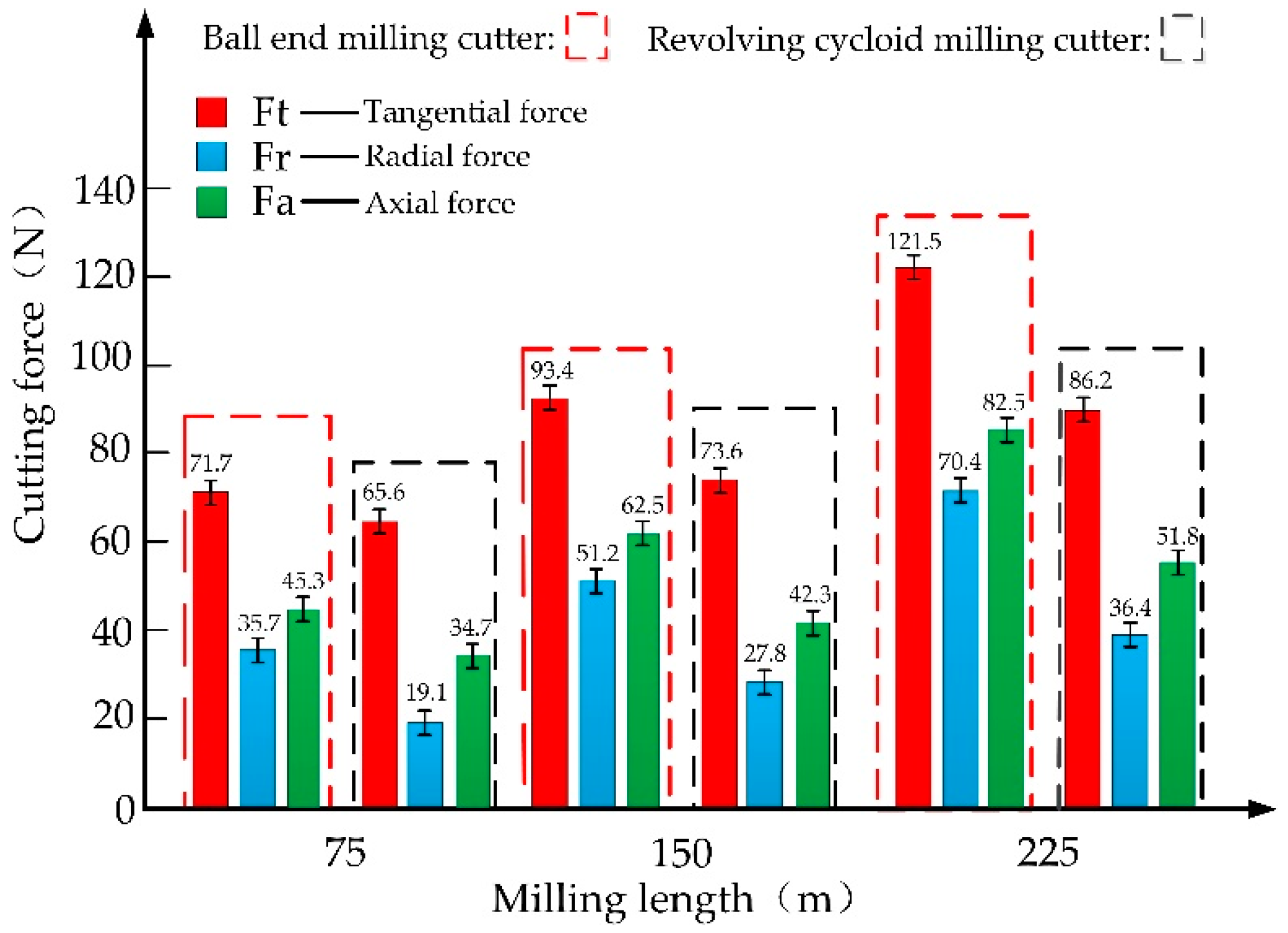
4.2.1. Effects of Tool Wear on Cutting Force
4.2.2. Tool Wear
4.2.3. Effects of Tool Wear on Machining Surface Topography
5. Conclusions
- Based on the established mathematical model of the contour surface of the revolving cycloid milling cutter, a parametric equation of the orthogonal helix cutting edge has been proposed to numerically simulate the established contour and edge line model. Advantages of the revolving cycloid milling cutter over the equivalent cutting helix angle and the scallop height of the workpiece surface have been proved by simulated results.
- The bottom boundary curve of the rake face was introduced. Based on the cutting edge equation and coordinate transformation, the five-axis grinding trajectory equation of the revolving cycloid milling cutter for rake face has been derived. The studies on grinding and detection of revolving cycloid milling cutter were carried out, and the quantitative evaluation of the grinding accuracy of the developed cutter was realized.
- Tests on the cutting force of the cutting titanium alloy TC11 of the revolving cycloid milling cutter and the ball-end milling cutter were studied comparatively. It can be found that the revolving cycloid milling cutter can significantly lower the axial force, the tangential force and the ratio of the axial force to the tangential force. Even under tool wear conditions, its cutting forces in all directions were increased slowly, showing excellent cutting stability.
- Compared with the ball-end milling cutter, the wear land of the revolving cycloid milling cutter in the cutting titanium alloy TC11 was narrow and long. As the wear sped up, the spoon-shaped wear gathering zone found in the ball-end milling cutter did not happen to the revolving cycloid milling cutter. The machining quality of the revolving cycloid milling cutter was relatively ideal.
Author Contributions
Funding
Conflicts of Interest
References
- Bing, W.; Liu, Z. Influences of tool structure, tool material and tool wear on machined surface integrity during turning and milling of titanium and nickel Alloys: A review. Int. J. Adv. Manuf. Technol. 2018, 98, 1925–1975. [Google Scholar]
- Sui, H.; Zhang, X.; Zhang, D.; Jiang, X.; Wu, R. Feasibility study of high-speed ultrasonic vibration cutting titanium alloy. J. Mater. Process. Technol. 2017, 247, 111–120. [Google Scholar] [CrossRef]
- Mishra, S.K.; Ghosh, S.; Aravindan, S. 3D finite element investigations on textured tools with different geometrical shapes for dry machining of titanium alloys. Int. J. Mech. Sci. 2018, 141, 424–449. [Google Scholar] [CrossRef]
- Tan, D.W.; Guo, W.M.; Wang, H.J.; Lin, H.T.; Wang, C.Y. Cutting performance and wear mechanism of TiB2-B4C ceramic cutting tools in high speed turning of Ti6Al4V alloy. Ceram. Int. 2018, 44, 15495–15502. [Google Scholar] [CrossRef]
- Hatt, O.; Lomas, Z.; Thomas, M.; Jackson, M. The effect of titanium alloy chemistry on machining induced tool crater wear characteristics. Wear 2018, 408, 200–207. [Google Scholar] [CrossRef]
- Ming, L.; Jing, W.; Wu, B.; Zhang, D. Effects of cutting parameters on tool insert wear in end milling of titanium alloy Ti6Al4V. J. Chin. J. Mech. Eng. 2017, 30, 53–59. [Google Scholar]
- Liu, X.L.; Jiang, Z.P.; Li, M.Y.; Ding, Y.; Wang, G.; Liu, L. New rounded end mill for mold processing based on scallop-height. J. Chin. J. Mech. Eng. 2015, 51, 192–204. [Google Scholar] [CrossRef]
- Jin, M.; Goto, I.; Watanabe, T.; Kurosawa, J.I.; Murakawa, M. Development of CBN ball-nosed end mill with newly designed cutting edge. J. Mater. Process. Technol. 2007, 192, 48–54. [Google Scholar] [CrossRef]
- Chen, T.; Wang, D.Y.; Li, S.Y.; Liu, X. Design, Manufacture and Grinding Accuracy Detection of PCBN Tools with Variable Chamfer Edge. J. Chin. J. Mech. Eng. 2018, 54, 214–221. [Google Scholar] [CrossRef]
- Pham, T.; Ko, S. A manufacturing model of an end mill using a five-axis CNC grinding machine. Int. J. Adv. Manuf. Technol. 2010, 48, 461–472. [Google Scholar] [CrossRef]
- Nguyen, H.; Ko, S.L. A Mathematical Model for Simulating and Manufacturing Ball End Mill. Comput. Aided Des. 2014, 50, 16–26. [Google Scholar] [CrossRef]
- Tan, L.; Yao, C.; Ren, J.; Zhang, D. Effect of Cutter Path Orientations on Cutting Forces, Tool Wear, and Surface Integrity When Ball End Milling TC17. Int. J. Adv. Manuf. Technol. 2016, 88, 2589–2602. [Google Scholar] [CrossRef]
- Krishnaraj, V.; Samsudeensadham, S.; Sindhumathi, R.; Kuppan, P. A study on High Speed End Milling of Titanium Alloy. Procedia Eng. 2014, 97, 251–257. [Google Scholar] [CrossRef] [Green Version]
- Oliaei, S.N.B.; Karpat, Y. Investigating the Influence of Built-up Edge on Forces and Surface Roughness in Micro Scale Orthogonal Machining of Titanium Alloy Ti6Al4V. J. Mater. Process. Technol. 2016, 235, 28–40. [Google Scholar] [CrossRef]
- Fromentin, G.; Poulachon, G. Geometrical analysis of thread milling—Part 1: Evaluation of tool angles. Int. J. Adv. Manuf. Technol. 2010, 49, 73–80. [Google Scholar] [CrossRef]
- Li, G.; Sun, J.; Li, J. Modeling and analysis of helical groove grinding in end mill machining. J. Mater. Process. Technol. 2014, 214, 3067–3076. [Google Scholar] [CrossRef]
- Rababh, M.; Almagableh, A.; Aljarrah, M. Five-axis rake face grinding of end-mills with circular-arc generators. Int. J. Interact. Des. Manuf. 2017, 11, 93–101. [Google Scholar] [CrossRef]
- Chen, F.; Hu, S.; Yin, S. A novel mathematical model for grinding ball-end milling cutter with equal rake and clearance angle. Int. J. Adv. Manuf. Technol. 2012, 63, 109–116. [Google Scholar] [CrossRef]
- Kim, J.H.; Park, J.W.; Ko, T.J. End mill design and machining via cutting simulation. Comput. Aided Des. 2008, 40, 324–333. [Google Scholar] [CrossRef]

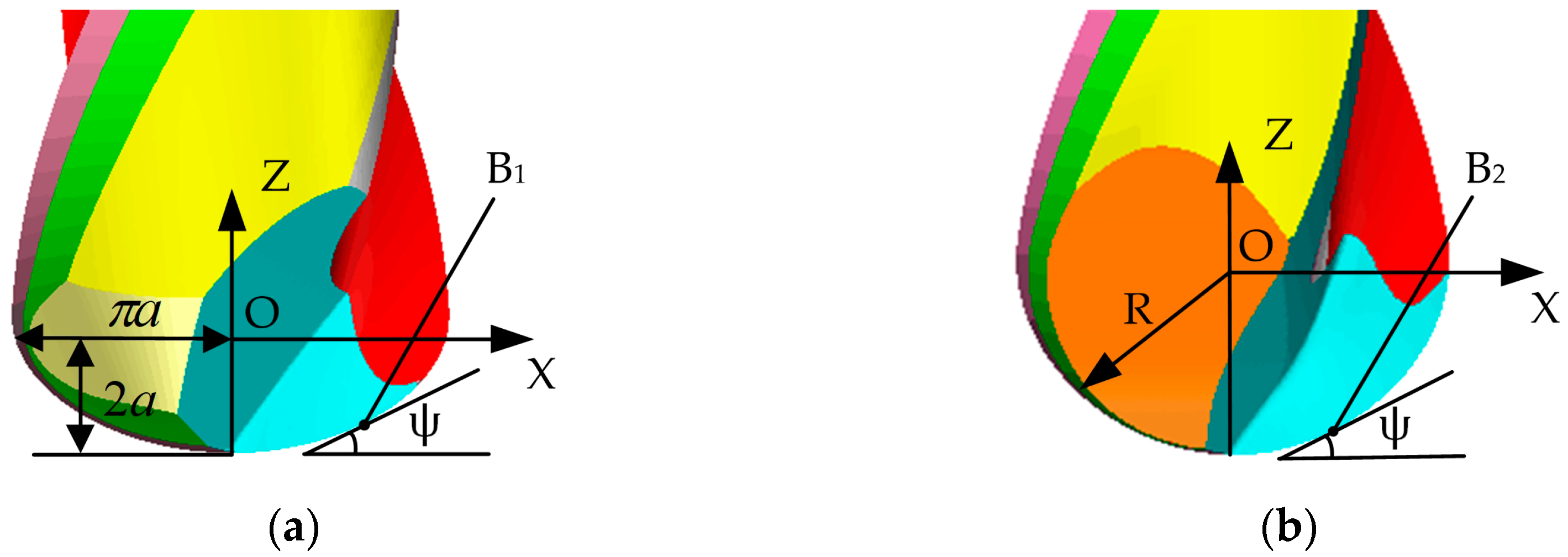







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Liu, X.; Gao, W.; Yan, B.; Chen, T. Study on the Design and Cutting Performance of a Revolving Cycloid Milling Cutter. Appl. Sci. 2019, 9, 2915. https://doi.org/10.3390/app9142915
Wang G, Liu X, Gao W, Yan B, Chen T. Study on the Design and Cutting Performance of a Revolving Cycloid Milling Cutter. Applied Sciences. 2019; 9(14):2915. https://doi.org/10.3390/app9142915
Chicago/Turabian StyleWang, Guangyue, Xianli Liu, Weijie Gao, Bingxin Yan, and Tao Chen. 2019. "Study on the Design and Cutting Performance of a Revolving Cycloid Milling Cutter" Applied Sciences 9, no. 14: 2915. https://doi.org/10.3390/app9142915
APA StyleWang, G., Liu, X., Gao, W., Yan, B., & Chen, T. (2019). Study on the Design and Cutting Performance of a Revolving Cycloid Milling Cutter. Applied Sciences, 9(14), 2915. https://doi.org/10.3390/app9142915



