Using the Characteristics of Pulse Waveform to Enhance the Accuracy of Blood Pressure Measurement by a Multi-Dimension Regression Model
Abstract
:1. Introduction
2. Methods
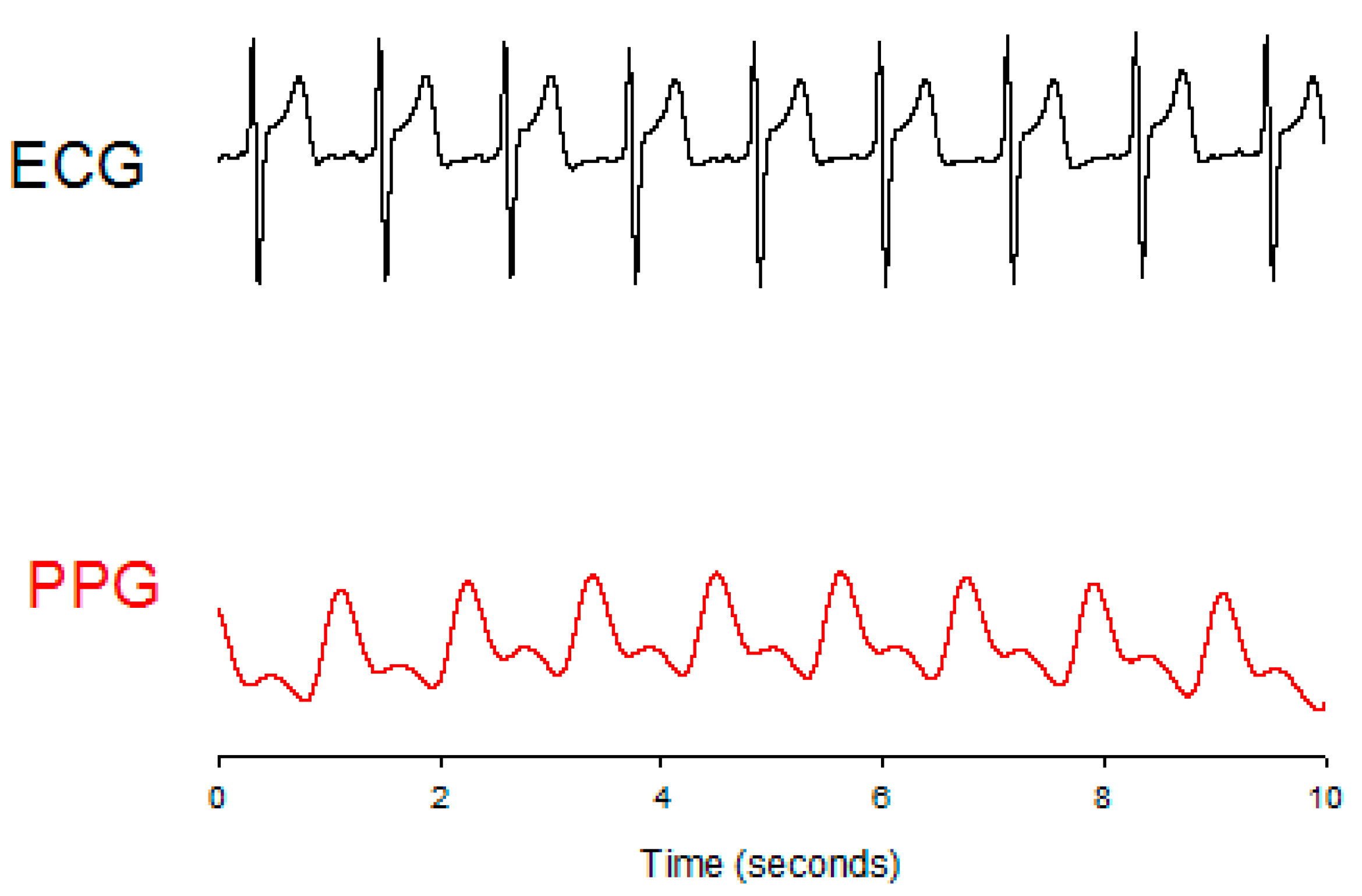
2.1. Parameters of the Pulse Wave
2.2. Multi-Dimension Regression Model
2.3. Deep Neural Network
2.4. Experimental Protocol
- The signals in the first five minutes were used as the baseline of the experiment. At the same time, the blood pressure was measured once and its finish-time would be marked at the PPG signal.
- The pedaling speed was about 80 rpm and was kept continuous for at least five minutes.
- Then, the blood pressure was measured and its finish-time would be marked at the PPG signal.
- Subjects were requested to rest and to wait for their blood pressure to drop to the baseline. The blood pressures of the subjects were measured repeatedly once every minute within the resting duration, and its finish-time would be marked at the PPG signal.
- Repeat steps 1 to 5, five times.
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Majumder, S.; Mondal, T.; Deen, M.J. Wearable sensors for remote health monitoring. Sensors 2017, 17, 130. [Google Scholar] [CrossRef] [PubMed]
- Tremper, K.K.; Barker, S.J. Pulse oximetry. Anesthesiology 1989, 70, 98–108. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.H.; Wang, J.J.; Su, C.H.; Tan, T.H. Development of a patch-type electrocardiographic monitor for real time heartbeat detection and heart rate variability analysis. J. Med. Biol. Eng. 2018, 38, 411–423. [Google Scholar] [CrossRef]
- Liu, S.H.; Chang, Y.J. Using accelerometers for physical actions recognition by a neural fuzzy network. Telemed. Health 2009, 15, 867–876. [Google Scholar] [CrossRef] [PubMed]
- Carr, J.J.; Brown, J.M. Introduction to Biomedical Equipment Technology, 4th ed.; Prentice Hal: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Ahlstrom, C.; Johansson, A.; Uhlin, F.; Länne, T.; Ask, P. Noninvasive investigation of blood pressure changes using the pulse wave transit time: A novel approach in the monitoring of hemodialysis patients. J. Artif. Org. 2005, 8, 192–197. [Google Scholar] [CrossRef] [PubMed]
- Sharwood-Smith, G.; Bruce, J.; Drummond, G. Assessment of pulse transit time to indicate cardiovascular changes during obstetric spinal anesthesia. Br. J. Anesth. 2006, 96, 100–105. [Google Scholar] [CrossRef]
- Wesseling, K.H.; Jansen, J.C.; Settels, J.J.; Schreuder, J.J. Computation of arrtic flow from pressure in humans using a nonlinear three-element model. J. Appl. Physiol. 1993, 74, 2566–2573. [Google Scholar] [CrossRef]
- Oliver, J.; Webb, D. Noninvasive assessment of arterial stiffness and risk of atherosclerotic events. Arterioscler. Thromb. Vasc. Biol. 2003, 23, 554–566. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Liu, J.; Chen, X.; Wang, Y.; Zhaoa, Z. Continuous blood pressure estimation based on multiple parameters from electrocardiogram and photoplethysmogram by Back-propagation neural network. Comput. Ind. 2017, 89, 50–59. [Google Scholar] [CrossRef]
- Wu, C.-M.; Chuang, C.-Y.; Chen, Y.-J.; Chen, S.-C. A new estimate technology of noninvasive continuous blood pressure measurement based on electrocardiograph. Adv. Mech. Eng. 2016, 8, 1–8. [Google Scholar] [CrossRef]
- Ruiz-Rodríguez, J.C.; Ruiz-Sanmartín, A.; Ribas, V.; Caballero, J.; García-Roche, A.; Riera, J.; Nuvials, X.; de Nadal, M.; de Sola-Morales, O.; Serra, J.; et al. Innovative continuous non-invasive cuffless blood pressure monitoring based on photoplethysmography technology. Intensive Care Med. 2013, 39, 1618–1625. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Chang, J-H. Deep belief networks ensemble for blood pressure estimation. IEEE Access 2017, 5, 9962–9972. [Google Scholar] [CrossRef]
- Liu, S.H.; Lin, T.H.; Cheng, D.C.; Wang, J.J. Assessment of stroke volume from brachial blood pressure using arterial characteristics. IEEE Trans. Biomed. Eng. 2015, 62, 2151–2157. [Google Scholar] [CrossRef] [PubMed]
- Tyan, C.C.; Liu, S.H.; Chen, J.Y.; Chen, J.J.; Liang, W.M. A novel noninvasive measurement technique for analyzing the pressure pulse waveform of the radial artery. IEEE Trans. Biomed. Eng. 2008, 55, 286–297. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.H.; Wang, J.J.; Su, C.H.; Cheng, D.C. Improvement of left ventricular ejection time measurement in the impedance cardiography combined with the reflection photoplethysmography. Sensors 2017, 18, 3036. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.-H.; Cheng, D.-C.; Su, C.-H. A cuffless blood pressure measurement based on the impedance plethysmography technique. Sensors 2017, 17, 1176. [Google Scholar] [CrossRef] [PubMed]
- British Standards Institution (BSI). Non-Invasive Sphygmomanometers-Part 4: Test Procedures to Determine the Overall System Accuracy of Automated Non-Invasive Sphygmomanometers; British Standards Institution (BSI): London, UK, 2009. [Google Scholar]




| Parameters | Formula |
|---|---|
| Ejection Time Ratio (ETR) | |
| Beat Duty (BD) | |
| Heart Rate (HR) | |
| Volume change during systolic cycle (Z0AS) | |
| Volume change during diastolic cycle (Z0DS) | |
| Volume during systolic cycle (Z0AA) | Area during T1 in the pulse wave. |
| Volume during diastolic cycle (Z0DA2) | Area during T3 in the pulse wave. |
| Maximum volume change during systolic cycle (DPPGp) | Peak between T4 and T5 in the differential wave of pulse. |
| Minimum volume change during diastolic cycle (DPPGv) | Valley at the end of T5 in the differential wave of pulse. |
| Pulse transit time (PTT) | Time interval from the systolic ending of the left ventricular to the specific position of the peripheral artery. |
| Parameters | Formula |
|---|---|
| Number of input feature vector (X) | 5 |
| Number of output feature vector (Y) | 1 |
| Number of hidden layers: | 9 |
| Number of the hidden unit on the hidden layers: | {12, 20, 50, 50, 30, 30, 20, 20, 15} |
| Learning rate for weight | 0.01 |
| Learning rate for biases of visible units | 0.01 |
| Learning rate for biases of hidden units | 0.01 |
| Momentum rate | 0.9 |
| Maximum epoch in the pre-training: | 10000 |
| Maximum epoch in the fine-training: | 10000 |
| Initial weights and biases: | randomly between [–1,1] |
| Subjects | Systolic Pressure (mmHg) | Diastolic Pressure (mmHg) | ||
|---|---|---|---|---|
| Max. | Min. | Max. | Min. | |
| 1 | 134 ± 11.3 | 105 ± 3.4 | 81 ± 3.3 | 69 ± 4.4 |
| 2 | 139 ± 4.7 | 112 ± 2.8 | 78 ± 2.8 | 66 ± 3.8 |
| 3 | 146 ± 8.3 | 116 ± 3.8 | 81 ± 2.1 | 67 ± 3.8 |
| 4 | 142 ± 5.6 | 116 ± 1.1 | 81 ± 3.8 | 62 ± 5.3 |
| 5 | 161 ± 17.1 | 124 ± 4.3 | 83 ± 4.8 | 67 ± 0.9 |
| 6 | 151 ± 12.5 | 114 ± 1.1 | 78 ± 2.9 | 66 ± 4.0 |
| 7 | 146 ± 6.0 | 117 ± 1.7 | 69 ± 4.4 | 57 ± 3.5 |
| 8 | 152 ± 4.8 | 124 ± 6.2 | 93 ± 2.7 | 81 ± 7.3 |
| 9 | 134 ± 8.5 | 105 ± 2.5 | 72 ± 5.8 | 61 ± 3.5 |
| 10 | 133 ± 3.5 | 108 ± 2.2 | 74 ± 1.5 | 65 ± 1.5 |
| Subjects (Samples) | Systolic Pressure ERMS (mmHg) | Diastolic Pressure ERMS (mmHg) |
|---|---|---|
| 1 (35) | 11.9 | 5.4 |
| 2 (41) | 5.5 | 4.7 |
| 3 (37) | 11.8 | 5.1 |
| 4 (43) | 5.5 | 5.1 |
| 5 (48) | 6.2 | 3.3 |
| 6 (35) | 5.6 | 4.4 |
| 7 (43) | 7.5 | 3.9 |
| 8 (32) | 13.4 | 3.7 |
| 9 (41) | 6.9 | 4.2 |
| 10 (38) | 8.0 | 5.5 |
| Mean ± SD | 8.2 ± 3.00 | 4.5 ± 0.75 |
| Subjects (Samples) | All Parameters ERMS (mmHg) | PTT HR BD Z0DA2 DPPGv ETR ERMS (mmHg) | PTT HR BD Z0DA2 DPPGv ERMS (mmHg) | |||
|---|---|---|---|---|---|---|
| Number of Parameters | 10 | 6 | 5 | |||
| DNN | MDR | DNN | MDR | DNN | MDR | |
| 1 (35) | 7.4 | 5.2 | 10.0 | 8.2 | 10.0 | 7.9 |
| 2 (41) | 10.3 | 4.8 | 8.5 | 4.3 | 8.5 | 4.2 |
| 3 (37) | 9.0 | 8.6 | 8.9 | 7.4 | 8.9 | 8.7 |
| 4 (43) | 7.4 | 4.4 | 7.4 | 4.7 | 7.4 | 4.6 |
| 5 (48) | 7.5 | 4.3 | 7.4 | 6.3 | 7.4 | 4.1 |
| 6 (35) | 10.3 | 7.3 | 10.3 | 6.3 | 10.3 | 6.1 |
| 7 (43) | 11.4 | 7.9 | 11.5 | 7.5 | 11.4 | 7.3 |
| 8 (32) | 12.9 | 16.1 | 12.9 | 13.7 | 12.9 | 13.6 |
| 9 (41) | 9.1 | 6.7 | 9.0 | 6.0 | 9.1 | 6.0 |
| 10 (38) | 9.3 | 7.3 | 9.3 | 6.9 | 9.2 | 6.9 |
| Mean ± SD | 9.5 ± 1.82 | 7.3 ± 3.46 | 9.5 ± 1.73 | 7.1 ± 2.60 | 9.5 ± 1.71 | 6.9 ± 2.81 |
| Subjects (samples) | All Parameters ERMS (mmHg) | HR PTT BD DPPGv ETR Z0DA2 ERMS (mmHg)ERMS (mmHg) | HR PTT BD DPPGv ETR ERMS (mmHg) | |||
|---|---|---|---|---|---|---|
| Number of Parameters | 10 | 6 | 5 | |||
| DNN | MDR | DNN | MDR | DNN | MDR | |
| 1 (35) | 5.3 | 3.8 | 5.2 | 3.6 | 5.1 | 3.5 |
| 2 (41) | 4.9 | 3.4 | 4.9 | 4.1 | 4.9 | 3.9 |
| 3 (37) | 4.1 | 4.2 | 4.1 | 4.0 | 4.1 | 4.8 |
| 4 (43) | 5.6 | 4.6 | 5.5 | 4.5 | 5.6 | 4.4 |
| 5 (48) | 3.7 | 3.8 | 3.7 | 3.4 | 3.6 | 3.4 |
| 6 (35) | 5.0 | 4.3 | 5.0 | 3.9 | 5.0 | 3.8 |
| 7 (43) | 4.9 | 4.1 | 4.9 | 3.6 | 5.0 | 3.7 |
| 8 (32) | 4.2 | 4.0 | 4.2 | 3.3 | 4.2 | 3.6 |
| 9 (41) | 4.7 | 4.0 | 4.6 | 3.8 | 4.7 | 3.6 |
| 10 (38) | 4.9 | 6.1 | 4.9 | 5.7 | 4.9 | 5.4 |
| Mean ± SD | 4.7 ± 0.58 | 4.2 ± 0.73 | 4.7 ± 0.55 | 4.0 ± 0.70 | 4.7 ± 0.58 | 4.0 ± 0.65 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.-H.; Liu, L.-J.; Pan, K.-L.; Chen, W.; Tan, T.-H. Using the Characteristics of Pulse Waveform to Enhance the Accuracy of Blood Pressure Measurement by a Multi-Dimension Regression Model. Appl. Sci. 2019, 9, 2922. https://doi.org/10.3390/app9142922
Liu S-H, Liu L-J, Pan K-L, Chen W, Tan T-H. Using the Characteristics of Pulse Waveform to Enhance the Accuracy of Blood Pressure Measurement by a Multi-Dimension Regression Model. Applied Sciences. 2019; 9(14):2922. https://doi.org/10.3390/app9142922
Chicago/Turabian StyleLiu, Shing-Hong, Li-Jen Liu, Kuo-Li Pan, Wenxi Chen, and Tan-Hsu Tan. 2019. "Using the Characteristics of Pulse Waveform to Enhance the Accuracy of Blood Pressure Measurement by a Multi-Dimension Regression Model" Applied Sciences 9, no. 14: 2922. https://doi.org/10.3390/app9142922
APA StyleLiu, S.-H., Liu, L.-J., Pan, K.-L., Chen, W., & Tan, T.-H. (2019). Using the Characteristics of Pulse Waveform to Enhance the Accuracy of Blood Pressure Measurement by a Multi-Dimension Regression Model. Applied Sciences, 9(14), 2922. https://doi.org/10.3390/app9142922








