Numerical Investigation of Jet Angle Effect on Airfoil Stall Control
Abstract
:1. Introduction
2. Methods
2.1. Flow Conditions
2.2. Numerical Methods
3. Results and Discussion
3.1. Static Airfoil Simulations
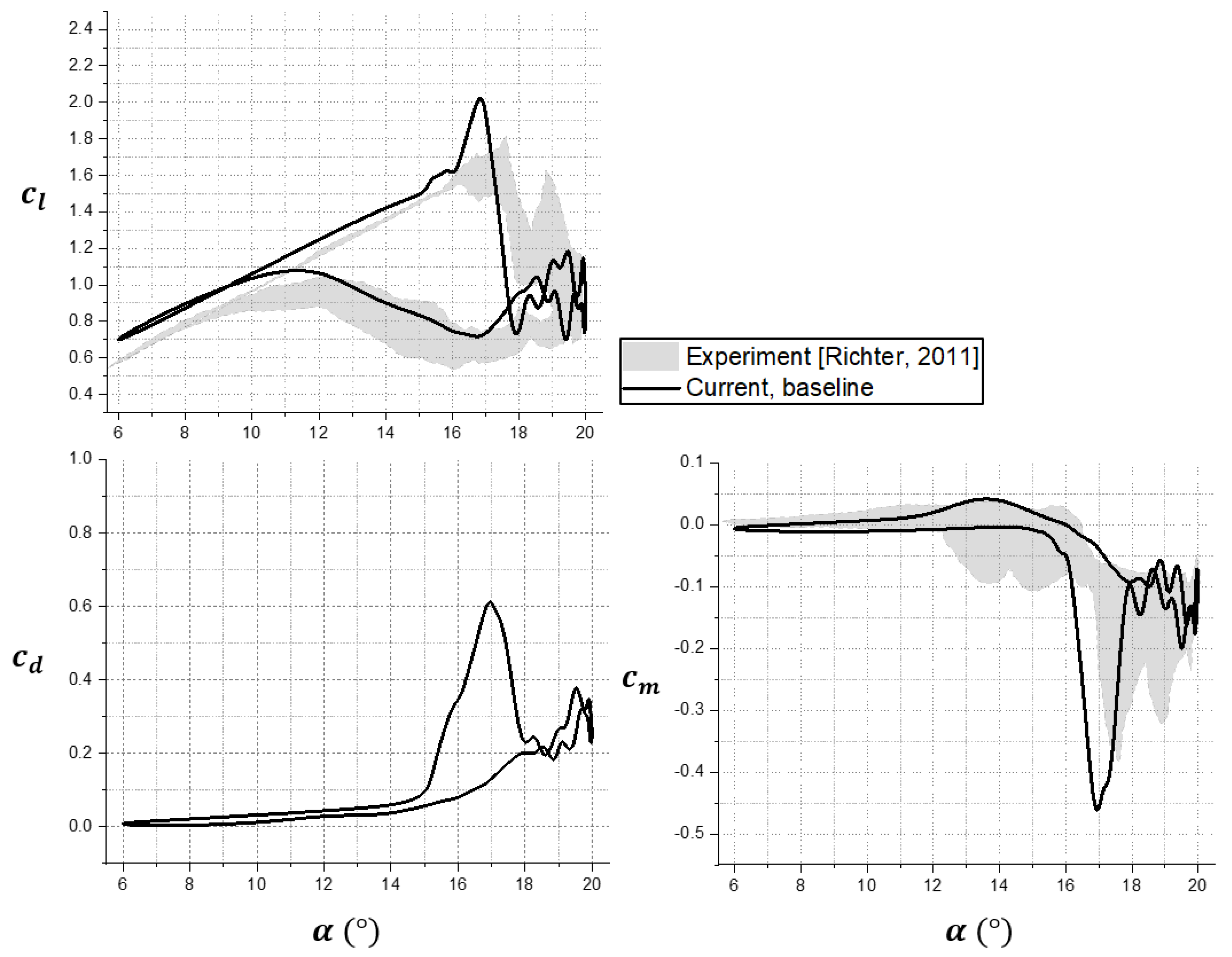
3.1.1. Baseline (No Flow Control)
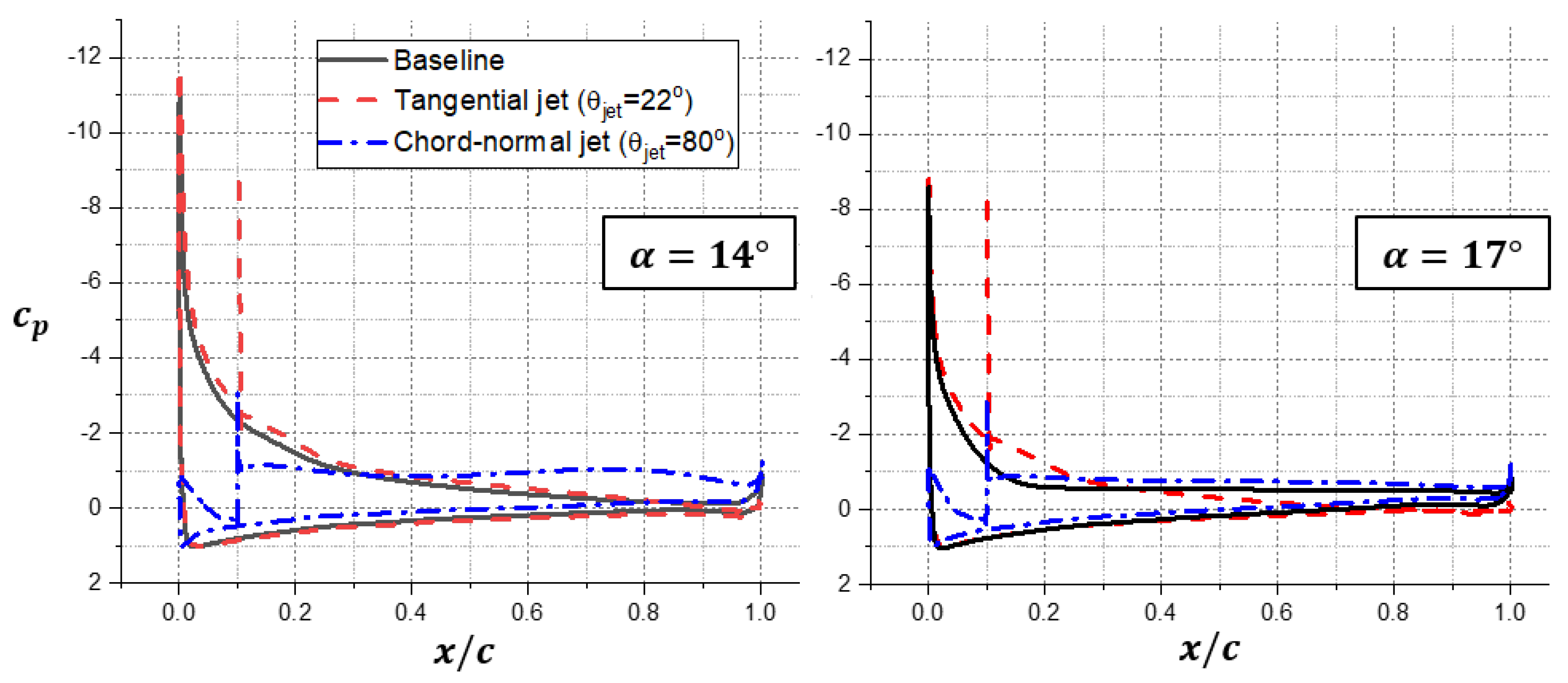
3.1.2. Flow Control
3.2. Pitching Airfoil Simulations
3.2.1. Baseline (No Flow Control)
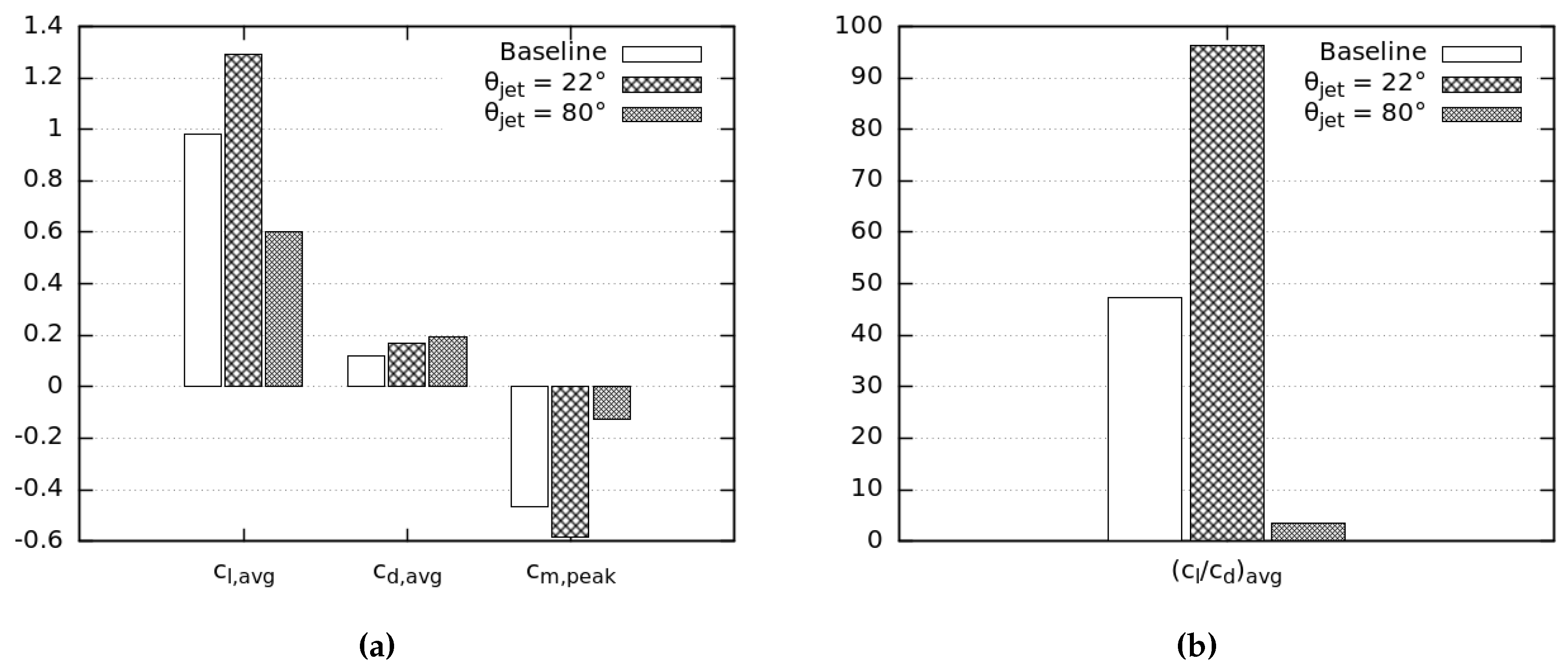
3.2.2. Flow Control
3.2.3. Estimate of Power Benefit with Jet Actuation
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| x | y | x | y | x | y | x | y |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.041108222 | 0.030856171 | 0.222157431 | 0.057684537 | 0.67639828 | 0.047832567 |
| 9.0018 × 10 | 0.001113223 | 0.04260152 | 0.031433287 | 0.233783757 | 0.057768554 | 0.689670934 | 0.046972394 |
| 0.000487097 | 0.002277455 | 0.044145829 | 0.032013403 | 0.247086417 | 0.05779856 | 0.701310262 | 0.046179236 |
| 0.00090018 | 0.003227646 | 0.045646129 | 0.032559512 | 0.258764753 | 0.057818564 | 0.71289958 | 0.045372074 |
| 0.001427285 | 0.00429786 | 0.048696739 | 0.033633727 | 0.280413083 | 0.057878576 | 0.726175235 | 0.04440188 |
| 0.00269754 | 0.006388278 | 0.051730346 | 0.03464993 | 0.293771754 | 0.057908582 | 0.741088218 | 0.043281656 |
| 0.004053811 | 0.008194639 | 0.054740948 | 0.035607121 | 0.307114423 | 0.05794859 | 0.75604821 | 0.042085417 |
| 0.004727946 | 0.008971794 | 0.057854571 | 0.036554311 | 0.320414083 | 0.057978596 | 0.769286857 | 0.040981196 |
| 0.00544809 | 0.009754951 | 0.062492498 | 0.03790058 | 0.343718744 | 0.057988598 | 0.784179836 | 0.039684937 |
| 0.00620124 | 0.010522104 | 0.065643129 | 0.038767754 | 0.355411082 | 0.057968594 | 0.800737147 | 0.038154631 |
| 0.007604521 | 0.011845369 | 0.068796759 | 0.03959792 | 0.370364073 | 0.057908582 | 0.81394979 | 0.036894379 |
| 0.008908782 | 0.012969594 | 0.071971394 | 0.04039808 | 0.385354071 | 0.05780156 | 0.833796759 | 0.034873975 |
| 0.010529106 | 0.014275855 | 0.078378676 | 0.041935387 | 0.400327065 | 0.05765153 | 0.856974395 | 0.032313463 |
| 0.011959392 | 0.015366073 | 0.08469994 | 0.04334867 | 0.413655731 | 0.057491498 | 0.8685007 | 0.03094919 |
| 0.012935587 | 0.016080216 | 0.094358872 | 0.045326065 | 0.428628726 | 0.057264453 | 0.883336667 | 0.029122825 |
| 0.014155831 | 0.016933387 | 0.097602521 | 0.045942188 | 0.443608722 | 0.057004401 | 0.903113623 | 0.026565313 |
| 0.015220044 | 0.017663533 | 0.115440088 | 0.049072815 | 0.456928386 | 0.056728346 | 0.918013603 | 0.024591918 |
| 0.016733347 | 0.018666733 | 0.125205041 | 0.050603121 | 0.466943389 | 0.056534307 | 0.942988598 | 0.021481296 |
| 0.018560712 | 0.019820964 | 0.131756351 | 0.051547309 | 0.483593719 | 0.056194239 | 0.947966593 | 0.020934187 |
| 0.019610922 | 0.020464093 | 0.13825065 | 0.052410482 | 0.496856371 | 0.055871174 | 0.956418284 | 0.020107021 |
| 0.02095119 | 0.021261252 | 0.14644929 | 0.05340068 | 0.520141028 | 0.055188038 | 0.964919984 | 0.019440888 |
| 0.023144629 | 0.022511502 | 0.152983597 | 0.054113823 | 0.540108022 | 0.054520904 | 0.968323665 | 0.019240848 |
| 0.024227846 | 0.023111622 | 0.162812563 | 0.055068014 | 0.55340068 | 0.054033807 | 0.975155031 | 0.018943789 |
| 0.025322064 | 0.023694739 | 0.172691538 | 0.055871174 | 0.570017003 | 0.053380676 | 0.978585717 | 0.018853771 |
| 0.027815563 | 0.024984997 | 0.179222845 | 0.056318264 | 0.581683337 | 0.05290058 | 0.983676735 | 0.018773755 |
| 0.02954891 | 0.025845169 | 0.185790158 | 0.056691338 | 0.598306661 | 0.052157431 | 0.990431086 | 0.018746749 |
| 0.031766353 | 0.026912382 | 0.192395479 | 0.0569984 | 0.611632326 | 0.051510302 | 1 | 0.018753751 |
| 0.035770154 | 0.028655731 | 0.200637127 | 0.057284457 | 0.639840968 | 0.050023005 | ||
| 0.038187638 | 0.029678936 | 0.208908782 | 0.057484497 | 0.661459292 | 0.048769754 |
| x | y | x | y | x | y | x | y |
|---|---|---|---|---|---|---|---|
| 1 | 0.014525905 | 0.615526105 | −0.02345169 | 0.20155031 | −0.029845969 | 0.009194839 | −0.013742749 |
| 0.990338068 | 0.014409882 | 0.602247449 | −0.024217844 | 0.188264653 | −0.029192839 | 0.007521504 | −0.012709542 |
| 0.981836367 | 0.014089818 | 0.587257451 | −0.02505201 | 0.178245649 | −0.028692739 | 0.005941188 | −0.011375275 |
| 0.978392679 | 0.013902781 | 0.564009802 | −0.026305261 | 0.16160232 | −0.027862573 | 0.005208042 | −0.010595119 |
| 0.974977996 | 0.013672735 | 0.537364473 | −0.027585517 | 0.146629326 | −0.027115423 | 0.004030806 | −0.009121824 |
| 0.971597319 | 0.013409682 | 0.517453491 | −0.028502701 | 0.13169934 | −0.02635227 | 0.003440688 | −0.008261652 |
| 0.968156631 | 0.013082617 | 0.50414783 | −0.029065813 | 0.116760352 | −0.02554811 | 0.002863573 | −0.007381476 |
| 0.957991598 | 0.012005401 | 0.482543509 | −0.029872975 | 0.098492699 | −0.024511902 | 0.001913383 | −0.005728146 |
| 0.949592919 | 0.010915183 | 0.470874175 | −0.030279056 | 0.081873375 | −0.023464693 | 0.00140028 | −0.004730946 |
| 0.937954591 | 0.00925185 | 0.457604521 | −0.030693139 | 0.058714743 | −0.021784357 | 0.000843169 | −0.003573715 |
| 0.923057612 | 0.00694839 | 0.445972194 | −0.030989198 | 0.043878776 | −0.020564113 | 0.000260052 | −0.002007401 |
| 0.901697339 | 0.003630726 | 0.434313863 | −0.031236247 | 0.041315263 | −0.020241048 | 0 | 0 |
| 0.87705241 | 2.0004 × 10 | 0.422714543 | −0.031439288 | 0.039434887 | −0.020064013 | ||
| 0.855704141 | −0.002823565 | 0.407714543 | −0.031669334 | 0.037834567 | −0.019896979 | ||
| 0.839240848 | −0.004837968 | 0.389344869 | −0.031933387 | 0.027858572 | −0.018716743 | ||
| 0.819423885 | −0.007088418 | 0.377742549 | −0.032076415 | 0.026288258 | −0.018486697 | ||
| 0.794611922 | −0.009664933 | 0.362762553 | −0.032179436 | 0.0234977 | −0.018040608 | ||
| 0.758221644 | −0.013055611 | 0.334446889 | −0.032333467 | 0.021991398 | −0.017770554 | ||
| 0.746616323 | −0.014069814 | 0.316133227 | −0.032413483 | 0.020794159 | −0.017533507 | ||
| 0.726712342 | −0.015720144 | 0.301157231 | −0.032426485 | 0.019016803 | −0.01715043 | ||
| 0.715110022 | −0.016646329 | 0.28784757 | −0.032369474 | 0.017583517 | −0.016806361 | ||
| 0.701823365 | −0.017680536 | 0.26795059 | −0.032113423 | 0.015913183 | −0.016363273 | ||
| 0.681929386 | −0.01915083 | 0.246379276 | −0.031609322 | 0.014275855 | −0.015863173 | ||
| 0.658684737 | −0.020741148 | 0.234746949 | −0.031243249 | 0.012479496 | −0.015223045 | ||
| 0.637124425 | −0.022131426 | 0.218183637 | −0.030606121 | 0.010739148 | −0.014502901 |
References
- Gault, D.E. A Correlation of Low-Speed, Airfoil-Section Stalling Characteristics with Reynolds Number and Airfoil Geometry; Technical Report NACA-TN-3963; National Advisory Committee for Aeronautics: Washington, DC, USA, 1957.
- Carr, L.W.; Chandrasekhara, M. Compressibility effects on dynamic stall. Prog. Aerosp. Sci. 1996, 32, 523–573. [Google Scholar] [CrossRef]
- Johnson, W. Rotorcraft Aeromechanics; Cambridge University Press: Cambridge, UK, 2013; chapter 8.7 Rotor Blade Airfoils; pp. 294–298. [Google Scholar]
- Leishman, J.G. Principles of Helicopter Aerodynamics; Cambridge University Press: Cambridge, UK, 2006; chapter 9. Dynamic Stall; pp. 525–566. [Google Scholar]
- Corke, T.C.; Thomas, F.O. Dynamic stall in pitching airfoils: Aerodynamic damping and compressibility effects. Annu. Rev. Fluid Mech. 2015, 47, 479–505. [Google Scholar] [CrossRef]
- Truong, K.V. Modeling Aerodynamics, Including Dynamic Stall, for Comprehensive Analysis of Helicopter Rotors. Aerospace 2017, 4, 21. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Q. Numerical Study on Dynamic-Stall Characteristics of Finite Wing and Rotor. Appl. Sci. 2019, 9, 600. [Google Scholar] [CrossRef]
- Harper, P.W.; Flanigan, R.E. Investigation of the Variation of Maximum Lift for a Pitching Airplane Model and Comparison with Flight Results; Technical Report NACA-TN-1734; National Advisory Committee for Aeronautics: Langley Field, VA, USA, 1948.
- Gadeberg, B.L. The Effect of Rate of Change of Angle of Attack on the Maximum Lift Coefficient of a Pursuit Airplane; Technical Report NACA-TN-2525; National Advisory Committee for Aeronautics: Moffett Field, CA, USA, 1951.
- Conner, F.; Twomey, W.; Willey, C. A Flight and Wind Tunnel Investigation of the Effect of Angle-of-Attack Rate on Maximum Lift Coefficient; Technical Report NASA-CR-321; NASA: Washington, DC, USA, 1965.
- Zhu, C.; Wang, T. Comparative Study of Dynamic Stall under Pitch Oscillation and Oscillating Freestream on Wind Turbine Airfoil and Blade. Appl. Sci. 2018, 8, 1242. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Yang, C.; Zhang, X.; Wang, Q.; Li, D.; Zhong, W.; Wang, T. Design and Testing of a LUT Airfoil for Straight-Bladed Vertical Axis Wind Turbines. Appl. Sci. 2018, 8, 2266. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Yang, K.; Xu, J.; Li, X. Aerodynamic Performance of Wind Turbine Airfoil DU 91-W2-250 under Dynamic Stall. Appl. Sci. 2018, 8, 1111. [Google Scholar] [CrossRef]
- Zhong, W.; Tang, H.; Wang, T.; Zhu, C. Accurate RANS Simulation of Wind Turbine Stall by Turbulence Coefficient Calibration. Appl. Sci. 2018, 8, 1444. [Google Scholar] [CrossRef]
- Lachmann, G.V. Boundary Layer and Flow Control; Pergamon Press: Oxford, UK, 1961. [Google Scholar]
- Gardner, A.D. Investigations of Dynamic Stall and Dynamic Stall Control on Helicopter Airfoils. Ph.D. Thesis, DLR, Deutsches Zentrum für Luft-und Raumfahrt, Cologne, Germany, 2016. [Google Scholar]
- Gardner, A.D.; Richter, K.; Mai, H.; Neuhaus, D. Experimental investigation of air jets for the control of compressible dynamic stall. J. Am. Helicopter Soc. 2013, 58, 1–14. [Google Scholar]
- Gardner, A.D.; Richter, K.; Mai, H.; Neuhaus, D. Experimental investigation of air jets to control shock-induced dynamic stall. J. Am. Helicopter Soc. 2014, 59, 1–11. [Google Scholar] [CrossRef]
- Gardner, A.D.; Richter, K.; Rosemann, H. Numerical investigation of air jets for dynamic stall control on the OA209 airfoil. CEAS Aeronaut. J. 2011, 1, 69. [Google Scholar] [CrossRef]
- Weaver, D.; McAlister, K.; Tso, J. Control of VR-7 dynamic stall by strong steady blowing. J. Aircr. 2004, 41, 1404–1413. [Google Scholar] [CrossRef]
- Matalanis, C.G.; Min, B.; Bowles, P.O.; Jee, S.; Wake, B.E.; Crittenden, T.M.; Woo, G.; Glezer, A. Combustion-powered actuation for dynamic-stall suppression: high-mach simulations and low-mach experiments. AIAA J. 2015, 53, 2151–2163. [Google Scholar] [CrossRef]
- Matalanis, C.G.; Bowles, P.O.; Min, B.; Jee, S.; Kuczek, A.E.; Wake, B.E.; Lorber, P.F.; Crittenden, T.M.; Glezer, A.; Schaeffler, N.W. High-Speed Experiments on Combustion-Powered Actuation for Dynamic Stall Suppression. AIAA J. 2017, 55, 3001–3015. [Google Scholar] [CrossRef]
- Jee, S.; Bowles, P.O.; Matalanis, C.G.; Min, B.; Wake, B.E.; Crittenden, T.; Glezer, A. Computations of Combustion-Powered Actuation for Dynamic Stall Suppression. In Proceedings of the 72nd American Helicopter Society (AHS) Annual Forum, West Palm Beach, FL, USA, 17–19 May 2016. [Google Scholar]
- Post, M.L.; Corke, T.C. Separation control on high angle of attack airfoil using plasma actuators. AIAA J. 2004, 42, 2177–2184. [Google Scholar] [CrossRef]
- Post, M.L.; Corke, T.C. Separation control using plasma actuators: dynamic stall vortex control on oscillating airfoil. AIAA J. 2006, 44, 3125–3135. [Google Scholar] [CrossRef]
- Amitay, M.; Smith, D.R.; Kibens, V.; Parekh, D.E.; Glezer, A. Aerodynamic flow control over an unconventional airfoil using synthetic jet actuators. AIAA J. 2001, 39, 361–370. [Google Scholar] [CrossRef]
- Sahni, O.; Wood, J.; Jansen, K.E.; Amitay, M. Three-dimensional interactions between a finite-span synthetic jet and a crossflow. J. Fluid Mech. 2011, 671, 254–287. [Google Scholar] [CrossRef]
- Chiatto, M.; Capuano, F.; de Luca, L. Numerical and experimental characterization of a double-orifice synthetic jet actuator. Meccanica 2018, 53, 2883–2896. [Google Scholar] [CrossRef]
- Rice, T.T.; Taylor, K.; Amitay, M. Wind tunnel quantification of dynamic stall on an S817 airfoil and its control using synthetic jet actuators. Wind Energy 2019, 22, 21–33. [Google Scholar] [CrossRef]
- Huang, L.; Huang, P.; LeBeau, R.; Hauser, T. Numerical study of blowing and suction control mechanism on NACA0012 airfoil. J. Aircr. 2004, 41, 1005–1013. [Google Scholar] [CrossRef]
- Duvigneau, R.; Hay, A.; Visonneau, M. Optimal location of a synthetic jet on an airfoil for stall control. J. Fluids Eng. 2007, 129, 825–833. [Google Scholar] [CrossRef]
- Poisson-Quinton, P.; Lepage, L. Survey of French research on the control of boundary layer and circulation. In Boundary Layer and Fow Control; Lachmann, G.V., Ed.; Pergamon Press: Oxford, UK, 1961; Volume 1, pp. 21–73. [Google Scholar]
- Attinello, J.S. Design and engineering features of flap blowing installations. In Boundary Layer and Flow Control; Lachmann, G.V., Ed.; Pergamon: Oxford, UK, 1961; Volume 1, pp. 463–515. [Google Scholar]
- Greenblatt, D.; Wygnanski, I.J. The control of flow separation by periodic excitation. Progr. Aerosp. Sci. 2000, 36, 487–545. [Google Scholar] [CrossRef]
- Greenblatt, D.; Wygnanski, I.J.; Rumsey, C.L. Aerodynamic Flow Control. In Encyclopedia of Aerospace Engineering; Blockley, R., Shyy, W., Eds.; Wiley: Hoboken, NJ, USA, 2010; Volume 1, Chapter 15; Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/9780470686652.eae019 (accessed on 31 May 2019).
- Mai, H.; Dietz, G.; Geibler, W.; Richter, K.; Bosbach, J.; Richard, H.; Groot, K. Dynamic stall control by leading edge vortex generators. J. Am. Helicopter Soc. 2008, 53, 26–36. [Google Scholar] [CrossRef]
- Richter, K.; Gardner, A.D.; Park, S. Numerical Investigation of the Influence of the Model Installation on Rotor Blade Airfoil Measurements. In New Results in Numerical and Experimental Fluid Mechanics IX; Springer: Berlin, Germany, 2014; pp. 225–233. [Google Scholar]
- Richter, K.; Pape, A.L.; Knopp, T.; Costes, M.; Gleize, V.; Gardner, A.D. Improved two-dimensional dynamic stall prediction with structured and hybrid numerical methods. J. Am. Helicopter Soc. 2011, 56, 1–12. [Google Scholar] [CrossRef]
- Economon, T.D.; Palacios, F.; Copeland, S.R.; Lukaczyk, T.W.; Alonso, J.J. SU2: An open-source suite for multiphysics simulation and design. AIAA J. 2015, 54, 828–846. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; Technical Report NASA/CR-2014-21878; National Aeronautics and Space Administration: Washington, DC, USA, 2014.
- Roe, P.L. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Venkatakrishnan, V. Convergence to steady state solutions of the Euler equations on unstructured grids with limiters. J. Comput. Phys. 1995, 118, 120–130. [Google Scholar] [CrossRef]
- Jameson, A. Time dependent calculations using multigrid, with applications to unsteady flows past airfoils and wings. In Proceedings of the AIAA 10th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 24–26 June 1991; p. 1596. [Google Scholar]
- Gardner, A.D.; Institute of Aerodynamics and Flow Technology, German Aerospace Center (DLR), Coln, Germany. Personal communication, 2018.
- Pape, A.L.; Costes, M.; Joubert, G.; David, F.; Deluc, J.M. Dynamic stall control using deployable leading-edge vortex generators. AIAA J. 2012, 50, 2135–2145. [Google Scholar] [CrossRef]
- Kim, T.; Kim, S.; Lim, J.; Kim, J.; Jee, S. Computational Study of Mach Number Effects on Dynamic Stall. In Proceedings of the ASME-JSME-KSME Joint Fluids Engineering Conference, San Francisco, CA, USA, 28 July–1 August 2019; p. 5536. [Google Scholar]















| Freestream (characteristic condition) | 56 kPa | |
| 304 K | ||
| 0.64 kg/m3 | ||
| 4 | ||
| Actuator (characteristic inflow) | 290 kPa | |
| 300 K | ||
| surface normal | ||
| 4 |
| Case | |||
|---|---|---|---|
| Static airfoil | No actuation | s | 30 |
| Jet actuation | s | 300 | |
| Pitching airfoil | No actuation | s | 150 |
| Jet actuation | s | 300 | |
| Case | Wjet [kW/m] | Wd [kW/m] | Wl [kW/m] | Wnet [kW/m] | ΔWnet [kW/m] |
|---|---|---|---|---|---|
| Baseline | 0 | 3.9 | 105.6 | 101.7 | 0 |
| Tangential jet | 17.2 | 6.7 | 137.6 | 113.7 | 12.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Park, Y.M.; Lee, J.; Kim, T.; Kim, M.; Lim, J.; Jee, S. Numerical Investigation of Jet Angle Effect on Airfoil Stall Control. Appl. Sci. 2019, 9, 2960. https://doi.org/10.3390/app9152960
Kim J, Park YM, Lee J, Kim T, Kim M, Lim J, Jee S. Numerical Investigation of Jet Angle Effect on Airfoil Stall Control. Applied Sciences. 2019; 9(15):2960. https://doi.org/10.3390/app9152960
Chicago/Turabian StyleKim, Junkyu, Young Min Park, Junseong Lee, Taesoon Kim, Minwoo Kim, Jiseop Lim, and Solkeun Jee. 2019. "Numerical Investigation of Jet Angle Effect on Airfoil Stall Control" Applied Sciences 9, no. 15: 2960. https://doi.org/10.3390/app9152960
APA StyleKim, J., Park, Y. M., Lee, J., Kim, T., Kim, M., Lim, J., & Jee, S. (2019). Numerical Investigation of Jet Angle Effect on Airfoil Stall Control. Applied Sciences, 9(15), 2960. https://doi.org/10.3390/app9152960




