Launch Bar Dynamics Character Analysis of Carrier-Based Aircraft Catapult Launch
Abstract
:1. Introduction
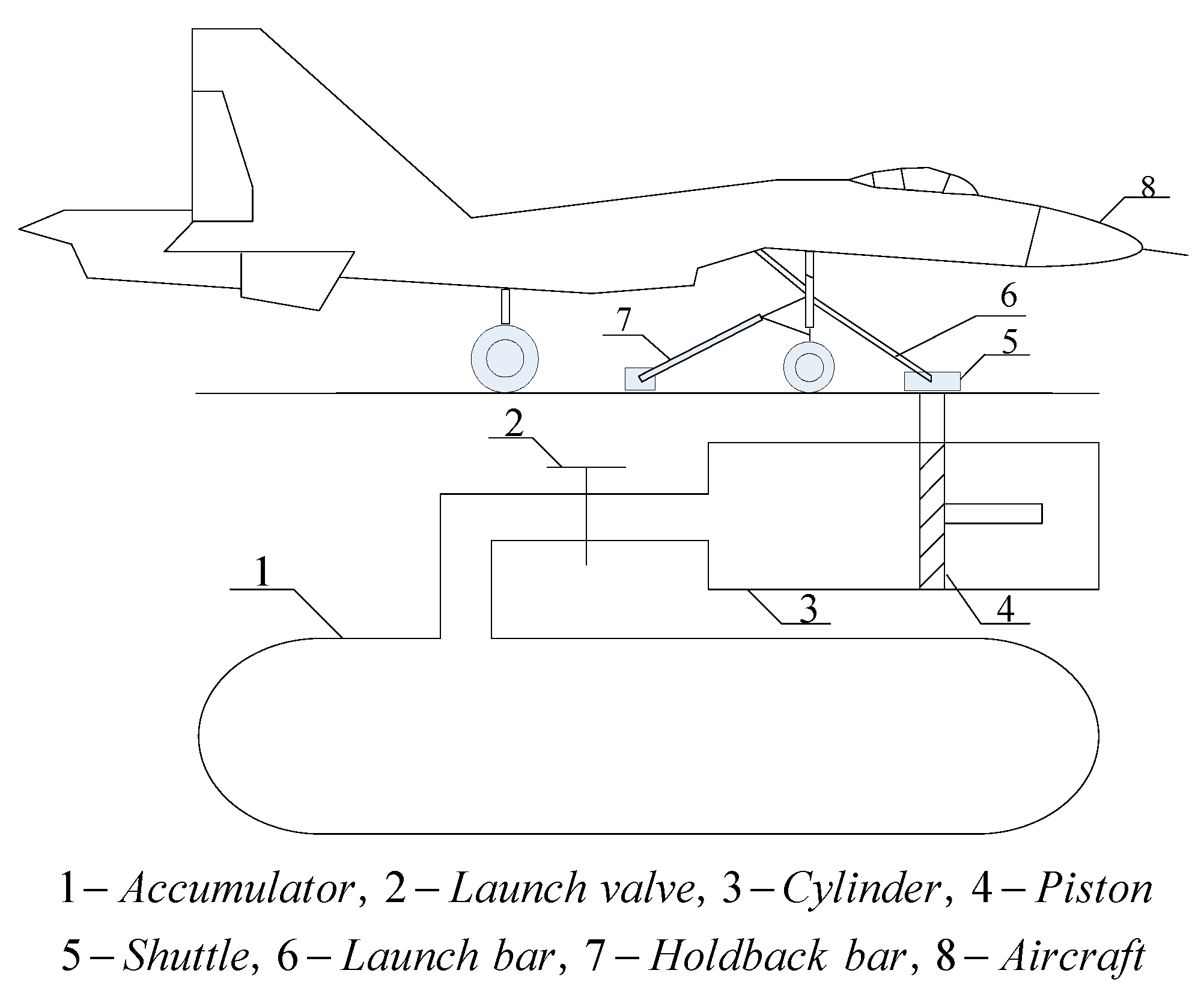
2. Mathematical Model of Catapult Launch
2.1. Modeling Assumptions
- The thermodynamic process of the steam catapult is an adiabatic process; the steam in the catapult is not affected by its environment.
- The accumulator, cylinder, and piston are rigid bodies, neglecting any changes in shape caused by temperature and pressure.
- The thermodynamic processes of the accumulator and cylinder are quasi-static processes.
- The steam has no friction with the pipe wall during the progress from accumulator to cylinder.
- The fuselage of the carrier-based aircraft is a rigid body.
- The deck motion and airflow interference are neglected.
- The carrier-based aircraft has no yaw angle during the process of catapult launch.
- The effects of asymmetric factors are not considered during the process of catapult launch.
- The nose gear is vertical with the flight deck surface of the carrier during the process of catapult launch.
- The elevator angle is fixed during the whole process of catapult launch.
- The force and damper model of the nose gear adopts the classical two-mass spring–damper model which divides the aircraft into two parts: the elastic support mass [36] and the inelastic support mass.
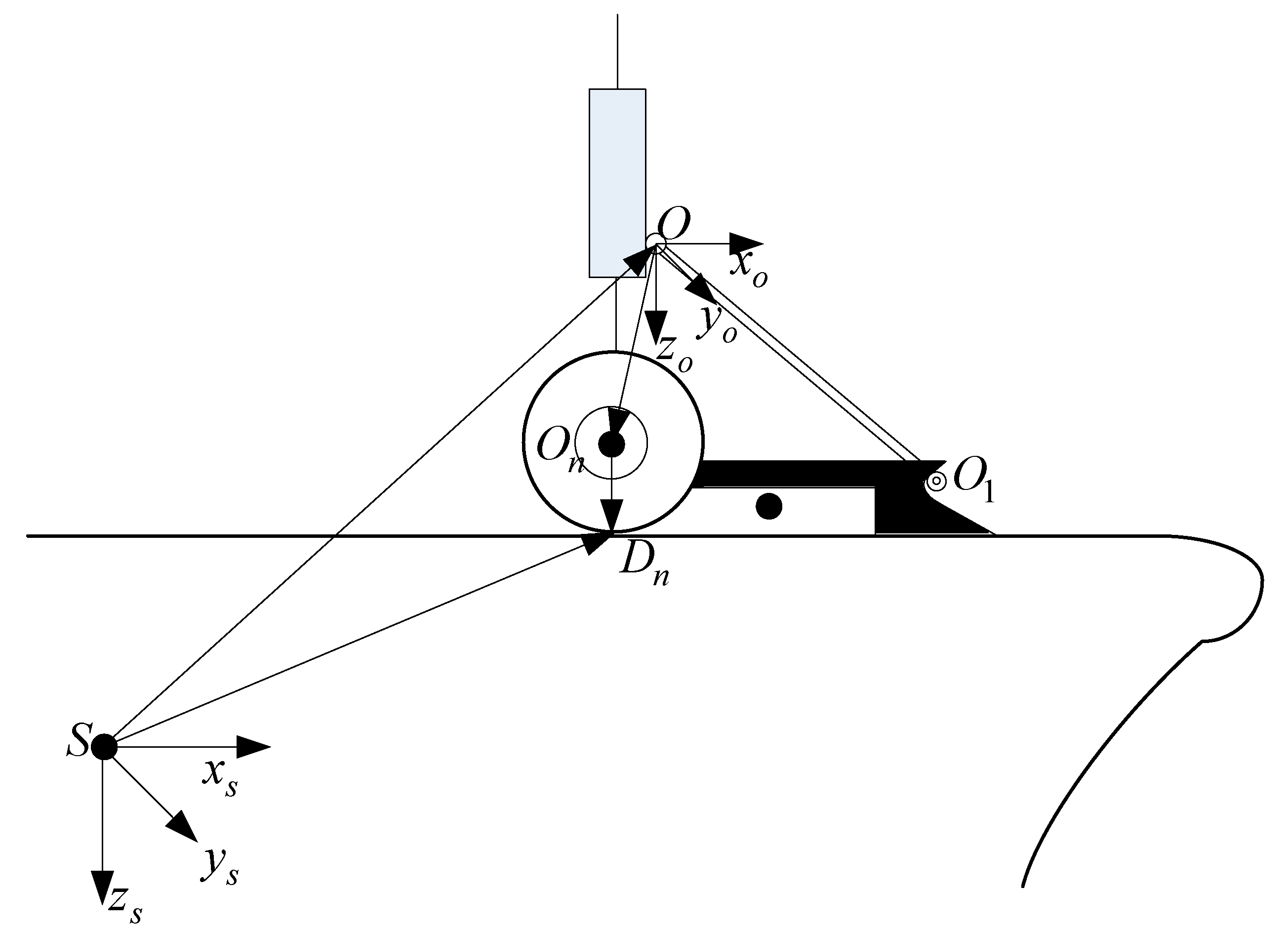
2.2. Mathematical Model of the Launch Bar
2.2.1. The Mathematical Model of the Launch Bar before the Launch Bar Automatically Disengages
2.2.2. The Mathematical Model of the Launch Bar after the Launch Bar Automatically Disengages
2.3. Mathematical Model of Other Sub-Modules
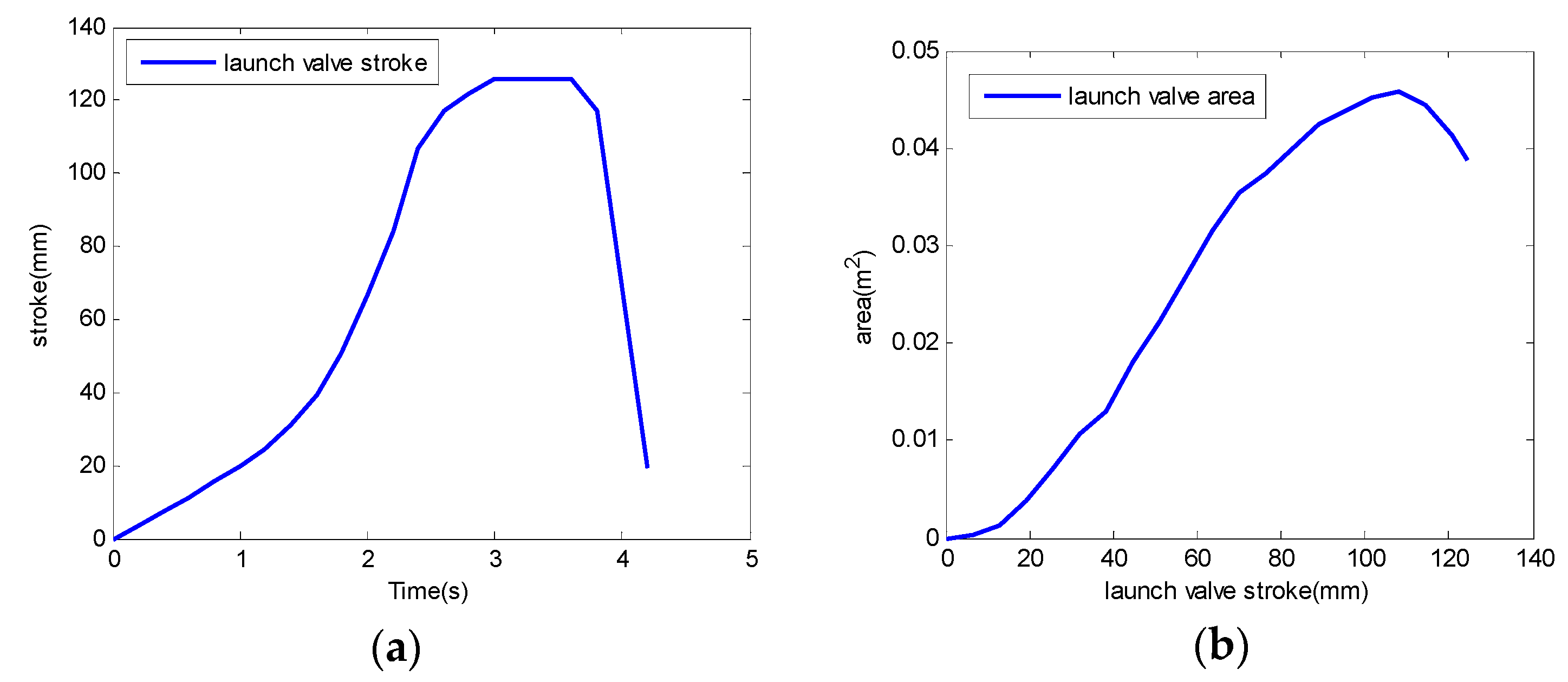
2.3.1. Mathematical Model of the Steam-Powered Catapult
2.3.2. Mathematical Model of the Holdback Bar
2.4. Staged Mathematical Model of the Catapult Launch
3. Results and Discussions
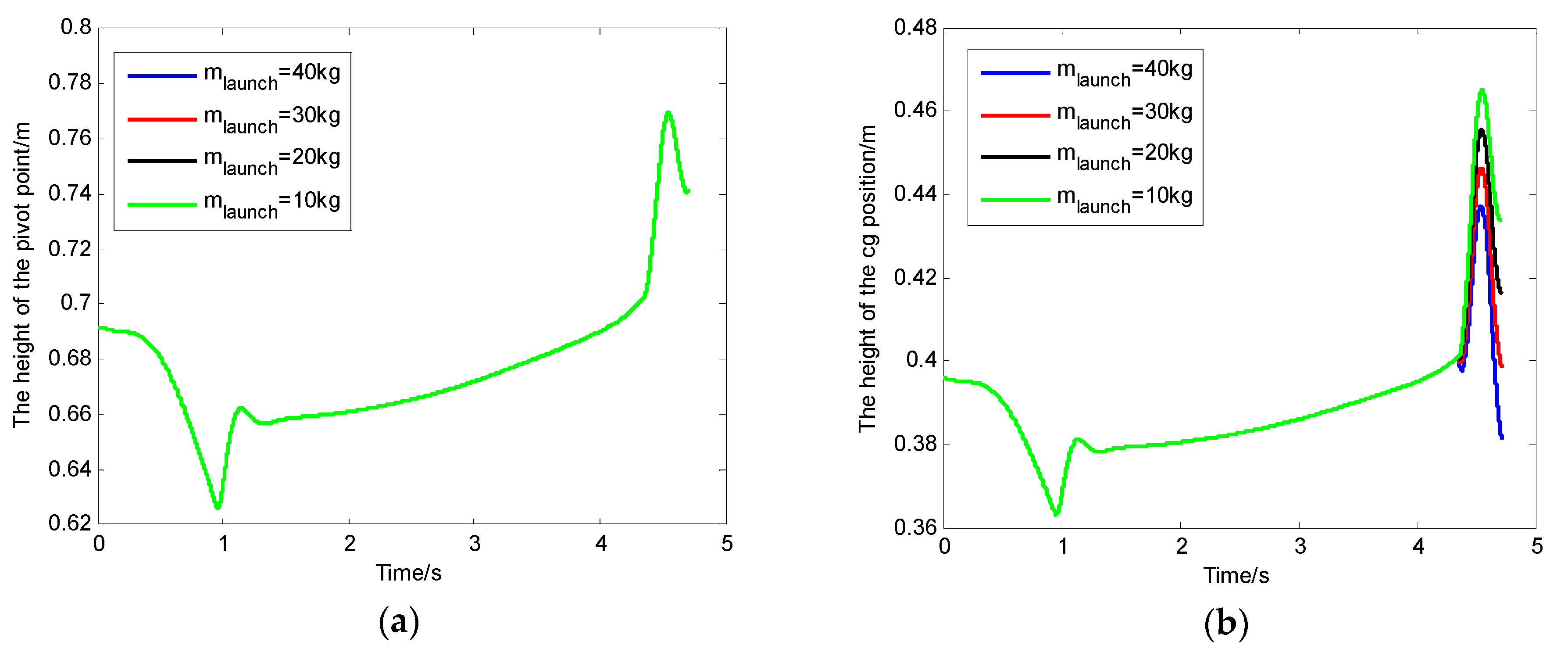
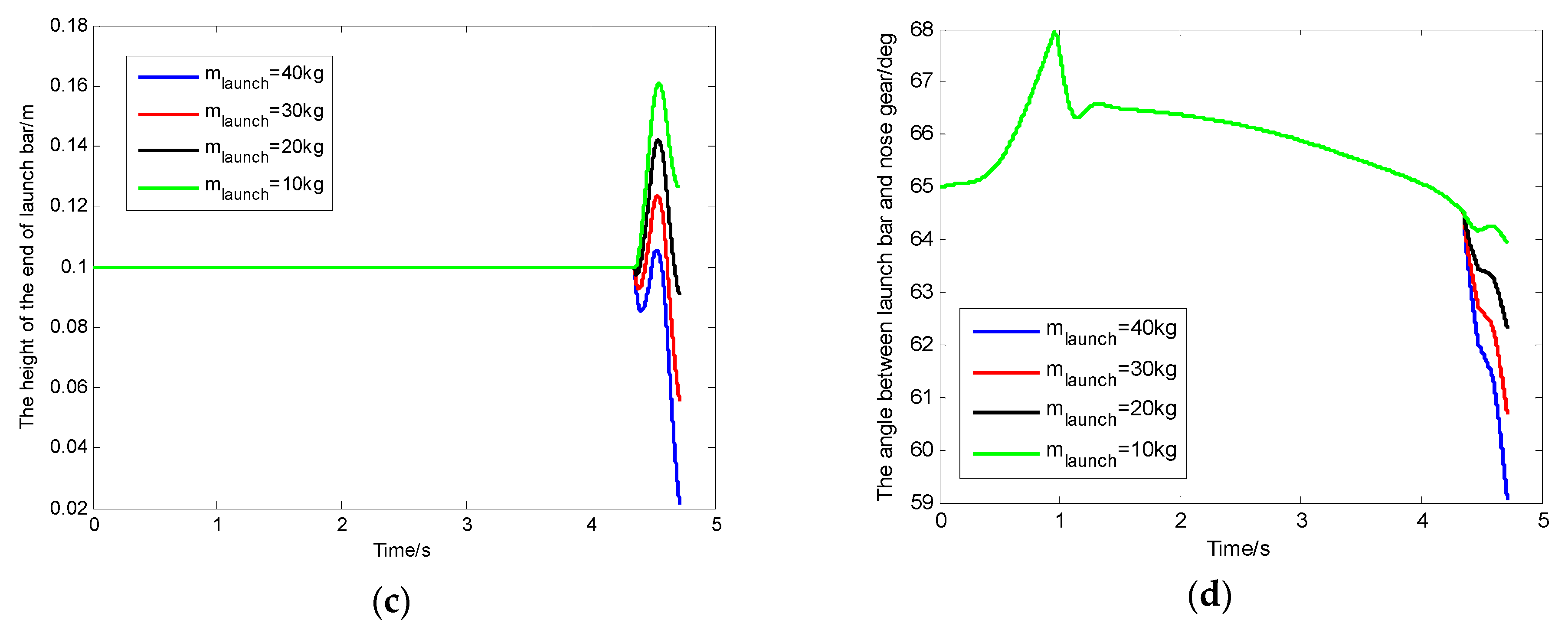
3.1. The Effect of the Launch Bar Mass on the Launch Bar Dynamics
3.2. The Effect of the Restoring Moment of the Launch Bar on the Launch Bar Dynamics
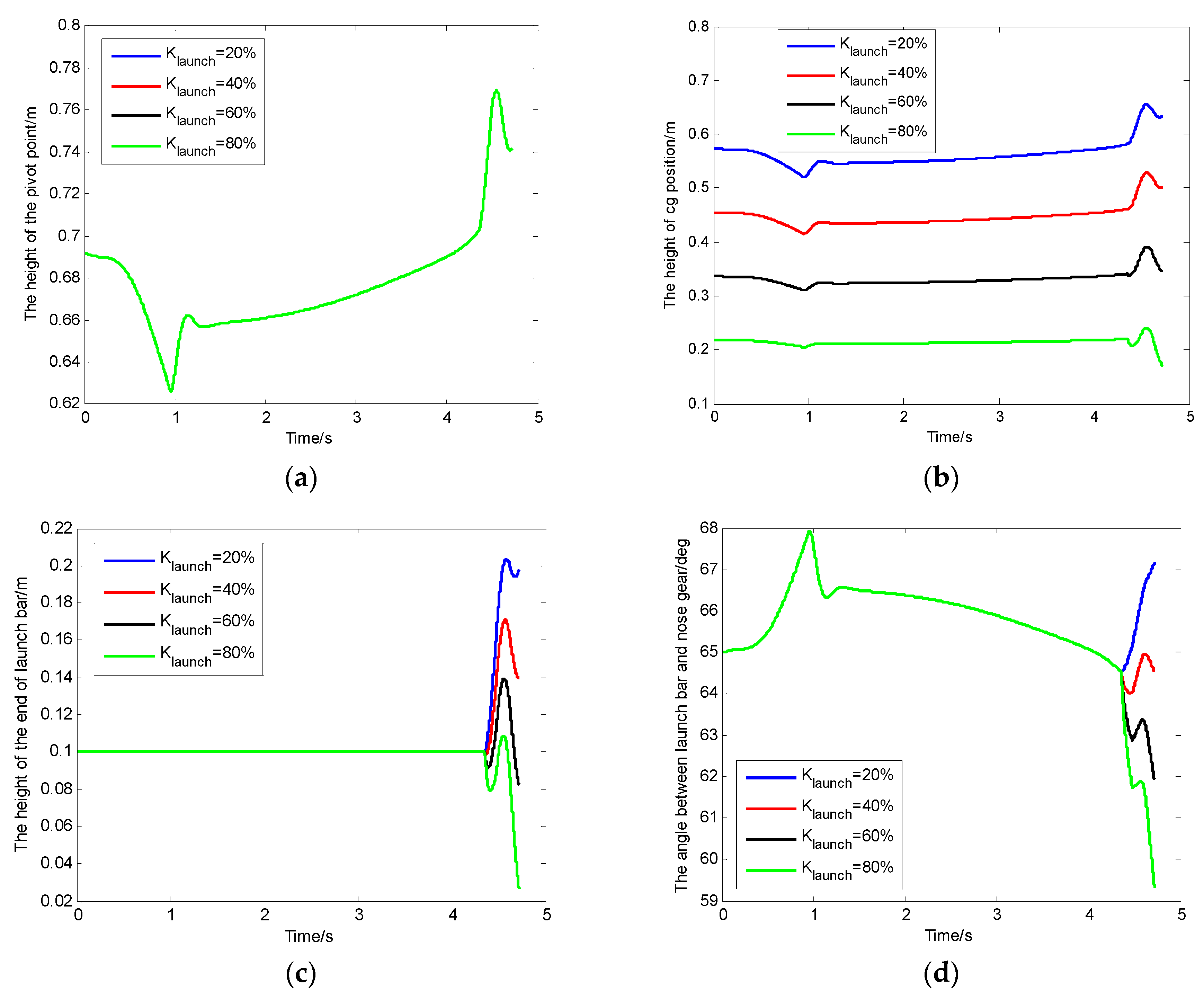
3.3. The Effect of the Launch Bar CG Position on the Launch Bar Dynamics
3.4. Contrastive Analysis of Each Influence Factor
4. Conclusions
- A complete mathematical model of catapult launch used to characterize the dynamics of the launch bar was established. Several experimental data from previous research were used to verify the proposed model. The mathematical model of catapult launch including the launch bar can be used to predict the dynamic behavior of the launch bar in order to avoid the launch bar striking the flight deck.
- The changes in launch bar mass, launch bar restoring moment, and launch bar proportionality factor had no effect on the height from the pivot point to the deck. We can reduce the risk of collision between the launch bar and the deck by reducing the mass of the launch bar, increasing the restoring moment, and shifting the cg position of the launch bar.
- Under the working conditions of this article, we increased the center of gravity position of the launch bar to control the sink of the launch bar end, which had the most obvious effect, and we reduced the mass of the launch bar, which had the least effect when controlling the sink of the launch bar end. Furthermore, reducing the mass of the launch bar can also greatly reduce the risk of collision between the launch bar and the deck. In order to avoid the risk of collision between the launch bar and the deck after the launch bar automatically disengages from the shuttle at the end of the power stroke, the restoring moment of the launch bar must overcome the sum of the other moments. It is worth noting that the degree of influence of these factors on the results of the final values of the launch bar end may change if the working conditions change.
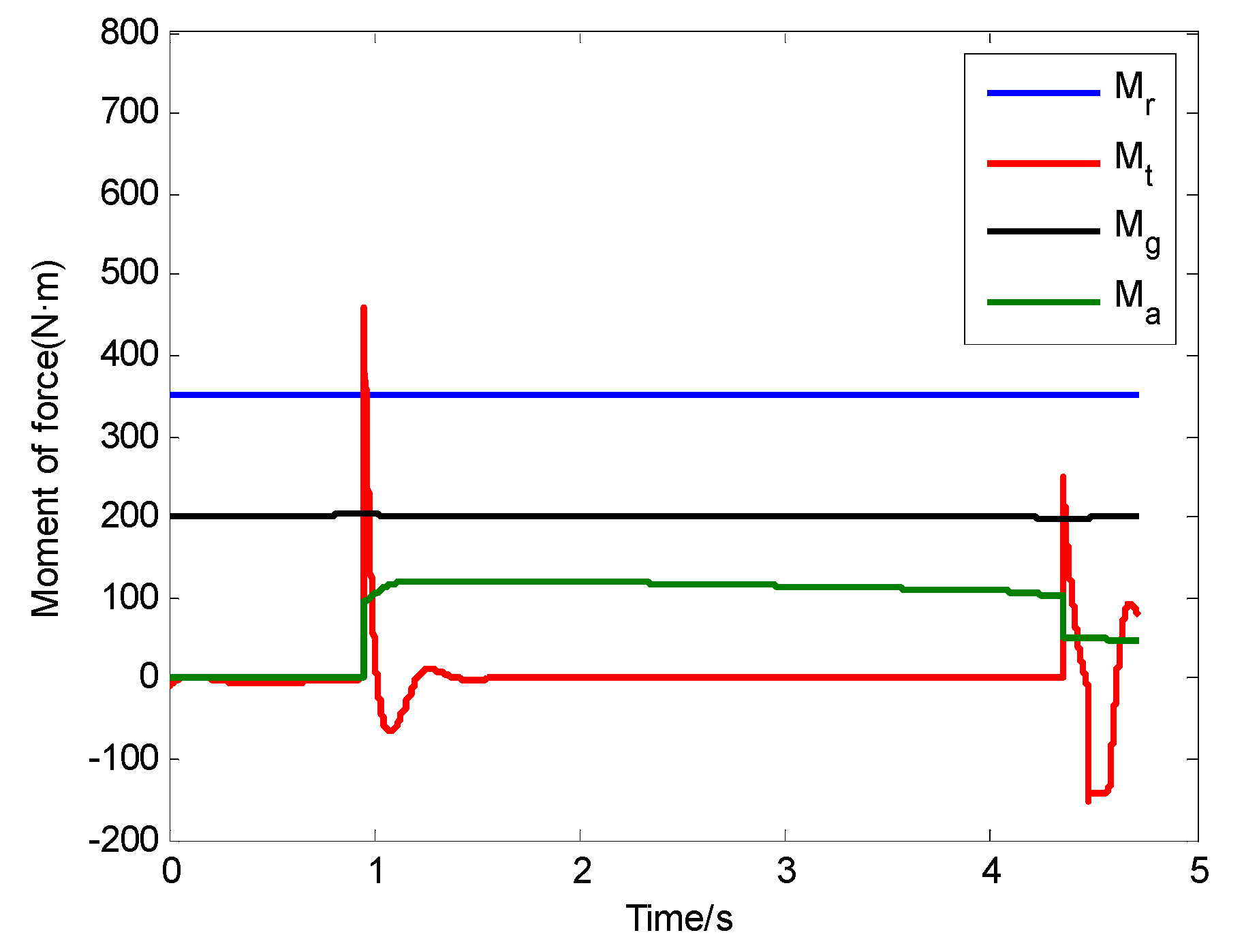
- The moment of the force of inertia due to the nose landing gear’s sudden extension changed greatly during the process of the free deck run. Furthermore, the first half of the moment of the force of inertia due to the nose landing gear’s sudden extension played a negative role, and the second half of it played a positive role. The moment of the force of inertia also changed greatly following the sudden discharge of the holdback load. In order to improve launching safety, we should pay attention to the nose landing gear’s sudden extension and the sudden discharge of the holdback load during the process of landing gear design.
- Selecting the optimal parameters for the launch bar is an important task, so as to control launching safety. The study results can give a theoretical reference for designing and testing the launch bars of carrier-based aircraft. It can also give a theoretical reference for designing and testing the launch bar’s driving mechanisms.
Author Contributions
Funding
Conflicts of Interest
References
- Naval Air Engineering Center. Mil-Std-2066(AS) Military Standard Catapulting and Arresting Gear Forcing Functions for Aircraft Structural Design; Department of the Navy Air Systems Command: Patuxent, MD, USA, 1981. [Google Scholar]
- Fang, X.; Nie, H.; Zhang, Z. Dynamic response analysis on carrier-based UAV considering catapult shuttle mass. Acta Aeronaut. Astronaut. Sin. 2018, 39, 200–208. [Google Scholar]
- Zhu, Q.; Lu, P.; Yang, Z. Simulation research on deadload steam catapult systems. J. Harbin Eng. Univ. 2018, 39, 1979–1986. [Google Scholar]
- Slavin, F.J. Aircraft steam catapult. Mech. Eng. 1969, 91, 42–46. [Google Scholar]
- Shi, Y.; Shi, T.; Ma, W.; Gao, C. Design and simulation of inner and outer cylinder-type steam catapult. Adv. Mech. Eng. 2018, 10, 1–7. [Google Scholar] [CrossRef]
- Sun, B.Z.; Guo, J.M.; Lei, Y.; Yang, L.B.; Li, Y.J.; Zhang, G.L. Simulation and verification of a non-equilibrium thermodynamic model for a steam catapult’s steam accumulator. Int. J. Heat Mass Transf. 2015, 85, 88–97. [Google Scholar] [CrossRef]
- Naval Air Engineering Center. Mil-L-22589d(AS) Launching System, Nose Gear Type, Aircraft; Navy Air Engineering Center: Lakehurst, NJ, USA, 1991. [Google Scholar]
- Small, D.B. Full scale tests of nose tow catapulting. In Proceedings of the 1st AIAA Annual Meeting, Washington, DC, USA, 29 June–2 July 1964. [Google Scholar]
- Yu, H.; Nie, H. Launch bar load analysis of carrier-based aircraft during off-center catapult launch. Acta Aeronaut. Astronaut. Sin. 2010, 31, 1953–1959. [Google Scholar]
- Huang, L. Research on Optimization Design Technology of Ejection Mechanism of a Carrier-Based Aircraft Nose Landing Gear. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. (In Chinese). [Google Scholar]
- Dennis, G.B.; Sidney, W.W. Aircraft and Devices for Launching Same. U.S. Patent 3,178,132, 13 April 1965. [Google Scholar]
- Boody, F.J. Aircraft Launching Mechanism. U.S. Patent 3,370,811, 27 February 1968. [Google Scholar]
- Smith, H.R. Launch Bar Installation. U.S. Patent 3,647,164, 7 March 1972. [Google Scholar]
- Derrien, M.; Ducos, D.; Engerand, J.L. Mechanism for Controlling a Catapult Bar. U.S. Patent 4,907,761, 13 March 1990. [Google Scholar]
- Wong, A.J. Nose Landing Gear Assembly for a Catapult Launched Airplane. U.S. Patent 5,732,906, 31 March 1998. [Google Scholar]
- Lucas, C.B. Catapult Criteria for a Carrier—Based Airplane; AD702814; Defense Technical Information Center: Fort Belvoir, WV, USA, 1968. [Google Scholar]
- Yu, H.; Nie, H. Dynamics Analysis of Carrier-Based Aircraft with Off-Center Catapult Launch. J. Nanjing Univ. Aeronaut. Astronaut. 2010, 42, 537–542. [Google Scholar]
- Yu, H.; Nie, H. Effects of off-center location on aircraft attitude during catapult launch. J. Beijing Univ. Aeronaut. Astronaut. 2011, 37, 10–14. [Google Scholar]
- Zhu, Q.; Liu, H.; Li, X. Research on carrier-based aircraft catapult launching in the case of different eccentricity. Flight Dyn. 2016, 34, 10–14. [Google Scholar]
- Lin, J.; Zhang, Y.; Le, T.; Wang, L. Effects of asymmetric factors to carrier-based aircraft catapult launch. J. Beijing Univ. Aeronaut. Astronaut. 2018, 44, 363–374. [Google Scholar]
- Wallace, M.M. F/A-18E/F Catapult Minimum End Airspeed Testing. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 2002. [Google Scholar]
- Loftus, J.; Piekarski, B. Carrier suitability tests of the rafale airplane in United States. In Proceedings of the Biennial Flight Test Conference, Hilton Head, SC, USA, 20–23 June 1994. [Google Scholar]
- Guo, Y.; Li, H.; Shen, G.; Yang, T. Modeling and analyze of the environmental factors of carrier-based aircraft catapult launch in complex environment. J. Beijing Univ. Aeronaut. Astronaut. 2011, 37, 877–881. [Google Scholar]
- Cai, L.; Jiang, J.; Wang, X.; Pan, T. Effects of deck motion on carrier-based aircraft’s catapult launching performance. Flight Dyn. 2014, 32, 105–109. [Google Scholar]
- Feng, Y.; Chen, B.; Zhang, B.; Xia, B.; Li, R. Influence factor analysis on the catapult launch of the carrier-based aircraft by the aircraft carrier’s vertical toss. Flight Dyn. 2019, 37, 22–27. [Google Scholar]
- Yan, C.; Feng, J. Automatic control flight for a carrier-based airplane in climb phase during catapult launch. J. Nanjing Univ. Aeronaut. Astronaut. 1995, 27, 431–438. [Google Scholar]
- Zhu, Y.; Jiang, J.; Zhen, Z.; Wang, X.; Jiao, X. Control law for climbing stage of carrier-based aircraft in catapult-assisted take-off. Electron. Opt. Control 2012, 19, 13–16. [Google Scholar]
- Lin, J.; Wang, L.; Yue, T. Lateral-directional flight control for single engine failure in catapult launch. In Proceedings of the 36th Chinese Control Conference, Dalian, China, 26–28 July 2017. [Google Scholar]
- Wu, W.; Song, L.; Zhang, Y.; Wang, J.; Gao, L. Analysis of factors affecting catapult take-off of carrier aircraft and design of lateral control law. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 662–671. [Google Scholar]
- Shen, Q.; Huang, Z. Sensitivity analysis of fast-extension performance of carrier based aircraft landing gear to varying parameters. Acta Aeronaut. Astronaut. Sin. 2010, 31, 532–537. [Google Scholar]
- Wei, X.; Liu, C.; Nie, H.; Zhang, M.; Yin, Q. Dynamics and test method of carrier-based aircraft nose landing gear sudden extension. Acta Aeronaut. Astronaut. Sin. 2013, 34, 1363–1369. [Google Scholar]
- Dou, Q.; Chen, Y.; Ma, X.; Mu, R. Experimental study on the sudden-extension performance of carrier-based aircraft landing gear. J. Vib. Eng. 2018, 31, 102–109. [Google Scholar]
- Liu, X.; Xu, D.; Wang, L. Match characteristics of aircraft-carrier parameters during catapult takeoff of carrier-based aircraft. Acta Aeronaut. Astronaut. Sin. 2010, 31, 102–108. [Google Scholar]
- Wilson, T. F-35 carrier suitability testing. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Zhu, Q.; Lu, P.; Yang, Z.; Ji, X.; Han, Y. Multi-Parameter Optimization for the Wet Steam Accumulator of a Steam-Powered Catapult. Energies 2019, 12, 234. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, X.; Yu, Y. Analysis of dynamic characteristics of catapult launch for a carrier-based aircraft with sudden load discharge. J. Harbin Eng. Univ. 2012, 33, 1150–1157. [Google Scholar]
- Zhu, Q.; Lu, P.; Yang, Z.; Cui, Y. Model research of steam catapult launch process for carrier-based aircraft. In Proceedings of the 37th Chinese Control Conference, Wuhan, China, 25–27 July 2018. [Google Scholar]
- U.S. Naval Air Engineering Center. Evaluation of Advanced Method for Steam Catapult Performance Prediction with Shipboard Test Data; AD742804; U.S. Naval Air Engineering Center: Lakehurst, NJ, USA, 1972. [Google Scholar]
- MIL-A-8863C. Airplane Strength and Rigidity Ground Loads for Navy Acquired Airplanes; United States Coast Guard: Washington, DC, USA, 1993. [Google Scholar]


| Simulation Conditions | Data |
|---|---|
| The type of aircraft | A3 |
| Mass of the aircraft | 31,752 kg |
| Thrust angle | 0° |
| Wing area | 72.37 m2 |
| Mean geometric chord | 3.55 m |
| Nose tire undeflected radius | 0.4 m |
| Main tire undeflected radius | 0.559 m |
| Initial steam pressure of accumulator | 1.38 MPa |
| The type of steam-powered catapult | C7 |
| Mass of piston | 3000 kg |
| Catapult stroke | 75.3 m |
| Deck edge distance | 12 m |
| The initial angle between the launch bar axis and deck | 30° |
| The initial angle between the holdback axis and deck | 25° |
| The coefficient of friction between the tire and deck surface | 0.17 |
| The coefficient of friction between the piston and cylinder wall | 0.17 |
| Air density | 1.2254 kg/m3 |
| Masses | 10 kg | 20 kg | 30 kg | 40 kg |
|---|---|---|---|---|
| 0.7693 m | 0.7693 m | 0.7693 m | 0.7693 m | |
| 0.4649 m | 0.4556 m | 0.4464 m | 0.4372 m | |
| 0.1607 m | 0.1420 m | 0.1235 m | 0.1055 m | |
| 0.7414 m | 0.7414 m | 0.7414 m | 0.7414 m | |
| 0.4338 m | 0.4164 m | 0.3988 m | 0.3817 m | |
| 0.1266 m | 0.0917 m | 0.0572 m | 0.0212 m | |
| 63.95° | 62.31° | 60.72° | 59.06° |
| Restoring Moments | 50 N·m | 150 N·m | 250 N·m | 350 N·m |
|---|---|---|---|---|
| 0.7693 m | 0.7693 m | 0.7693 m | 0.7693 m | |
| 0.4372 m | 0.4491 m | 0.4618 m | 0.4752 m | |
| 0.1055 m | 0.1289 m | 0.1551 m | 0.1836 m | |
| 0.7414 m | 0.7414 m | 0.7414 m | 0.7414 m | |
| 0.3814 m | 0.4035 m | 0.4261 m | 0.4492 m | |
| 0.0212 m | 0.0655 m | 0.1108 m | 0.1570 m | |
| 59.04° | 61.13° | 62.23° | 65.33° |
| Proportionality Factors | 20% | 40% | 60% | 80% |
|---|---|---|---|---|
| 0.7693 m | 0.7693 m | 0.7693 m | 0.7693 m | |
| 0.6555 m | 0.5294 m | 0.3912 m | 0.2408 m | |
| 0.2035 m | 0.1711 m | 0.1393 m | 0.1085 m | |
| 0.7414 m | 0.7414 m | 0.7414 m | 0.7414 m | |
| 0.6327 m | 0.5006 m | 0.3460 m | 0.1697 m | |
| 0.1978 m | 0.1395 m | 0.0824 m | 0.0267 m | |
| 67.15° | 64.54° | 61.92° | 59.30° |
| - | Mass Increases | Restoring Moment Decreases | Proportionality Factor Decreases |
|---|---|---|---|
| 1 | 0.1266 m | 0.1570 m | 0.1978 m |
| 2 | 0.0917 m | 0.1108 m | 0.1395 m |
| 3 | 0.0572 m | 0.0655 m | 0.0824 m |
| 4 | 0.0212 m | 0.0212 m | 0.0267 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Lu, P.; Yang, Z.; Ji, X.; Han, Y.; Wang, L. Launch Bar Dynamics Character Analysis of Carrier-Based Aircraft Catapult Launch. Appl. Sci. 2019, 9, 3079. https://doi.org/10.3390/app9153079
Zhu Q, Lu P, Yang Z, Ji X, Han Y, Wang L. Launch Bar Dynamics Character Analysis of Carrier-Based Aircraft Catapult Launch. Applied Sciences. 2019; 9(15):3079. https://doi.org/10.3390/app9153079
Chicago/Turabian StyleZhu, Qidan, Peng Lu, Zhibo Yang, Xun Ji, Yu Han, and Lipeng Wang. 2019. "Launch Bar Dynamics Character Analysis of Carrier-Based Aircraft Catapult Launch" Applied Sciences 9, no. 15: 3079. https://doi.org/10.3390/app9153079
APA StyleZhu, Q., Lu, P., Yang, Z., Ji, X., Han, Y., & Wang, L. (2019). Launch Bar Dynamics Character Analysis of Carrier-Based Aircraft Catapult Launch. Applied Sciences, 9(15), 3079. https://doi.org/10.3390/app9153079





