Failure Diagnosis of Demagnetization in Interior Permanent Magnet Synchronous Motors Using Vibration Characteristics
Abstract
:1. Introduction
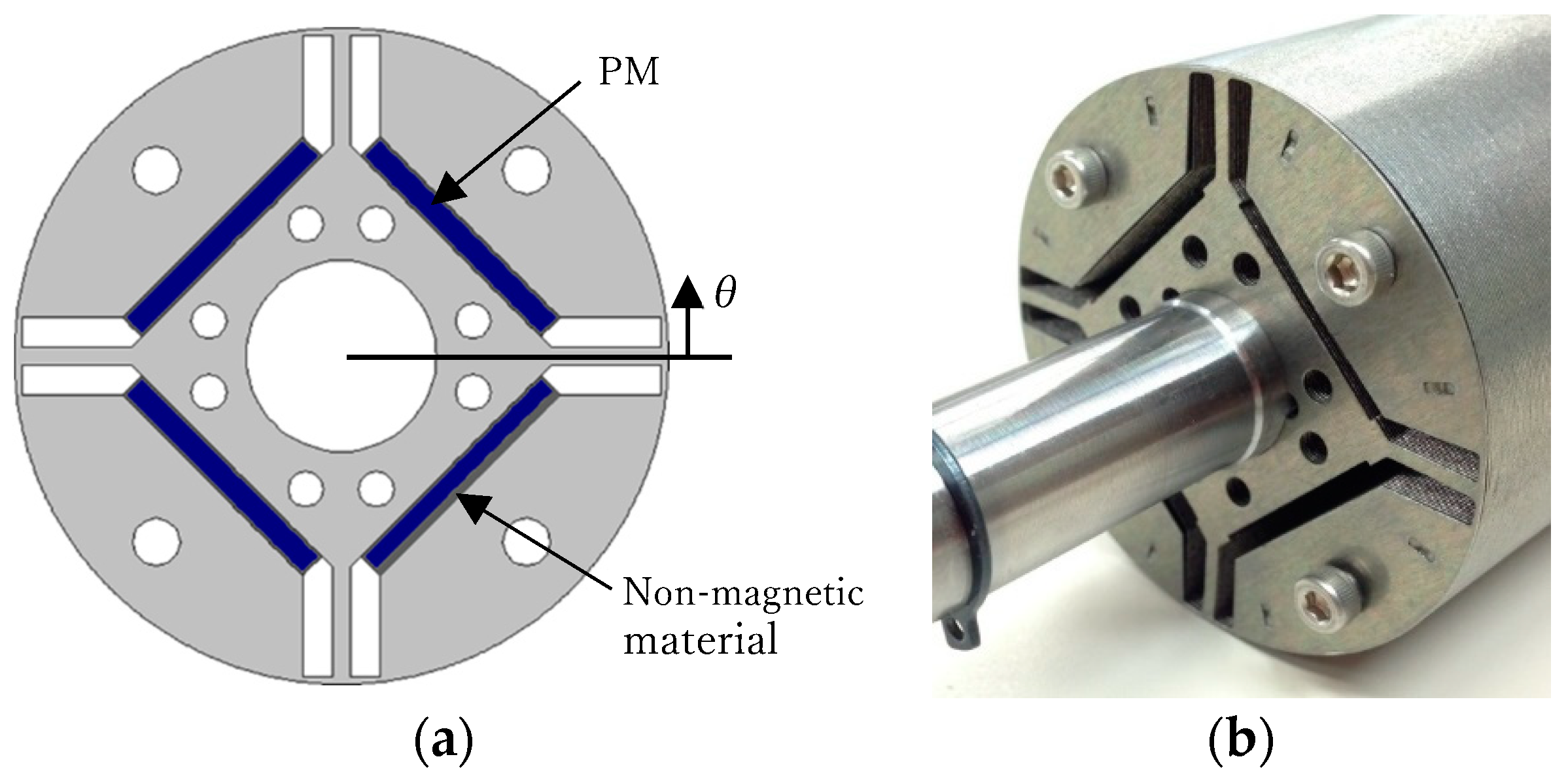
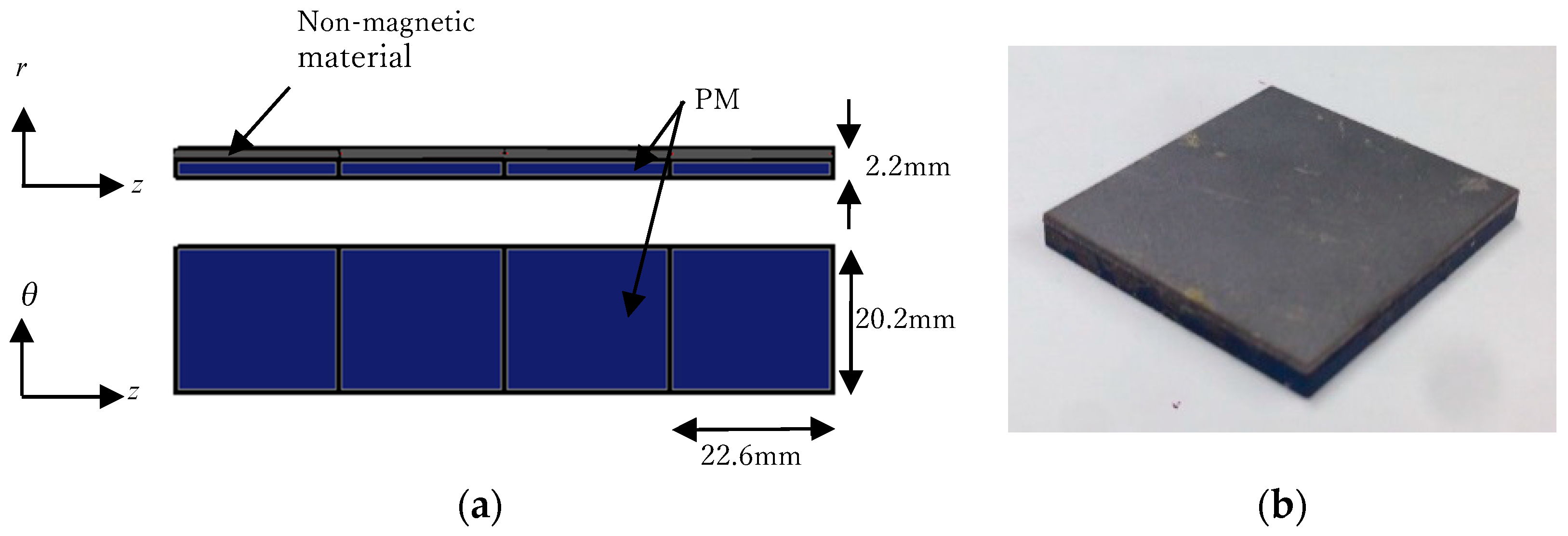
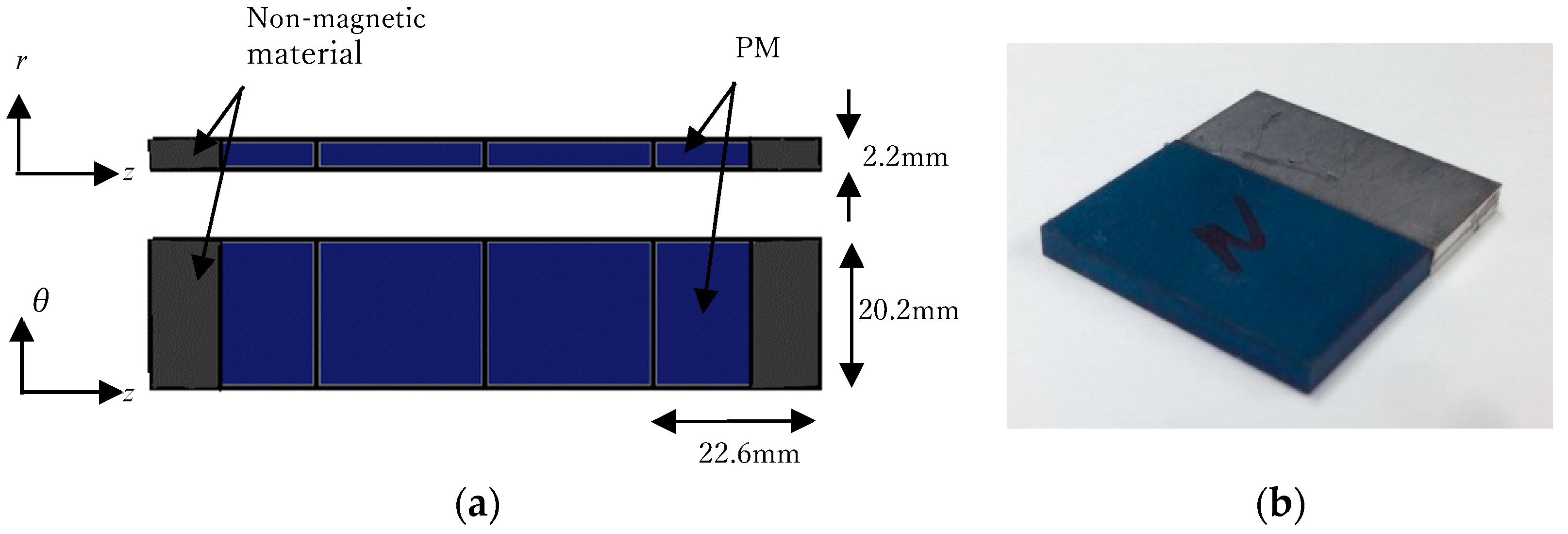
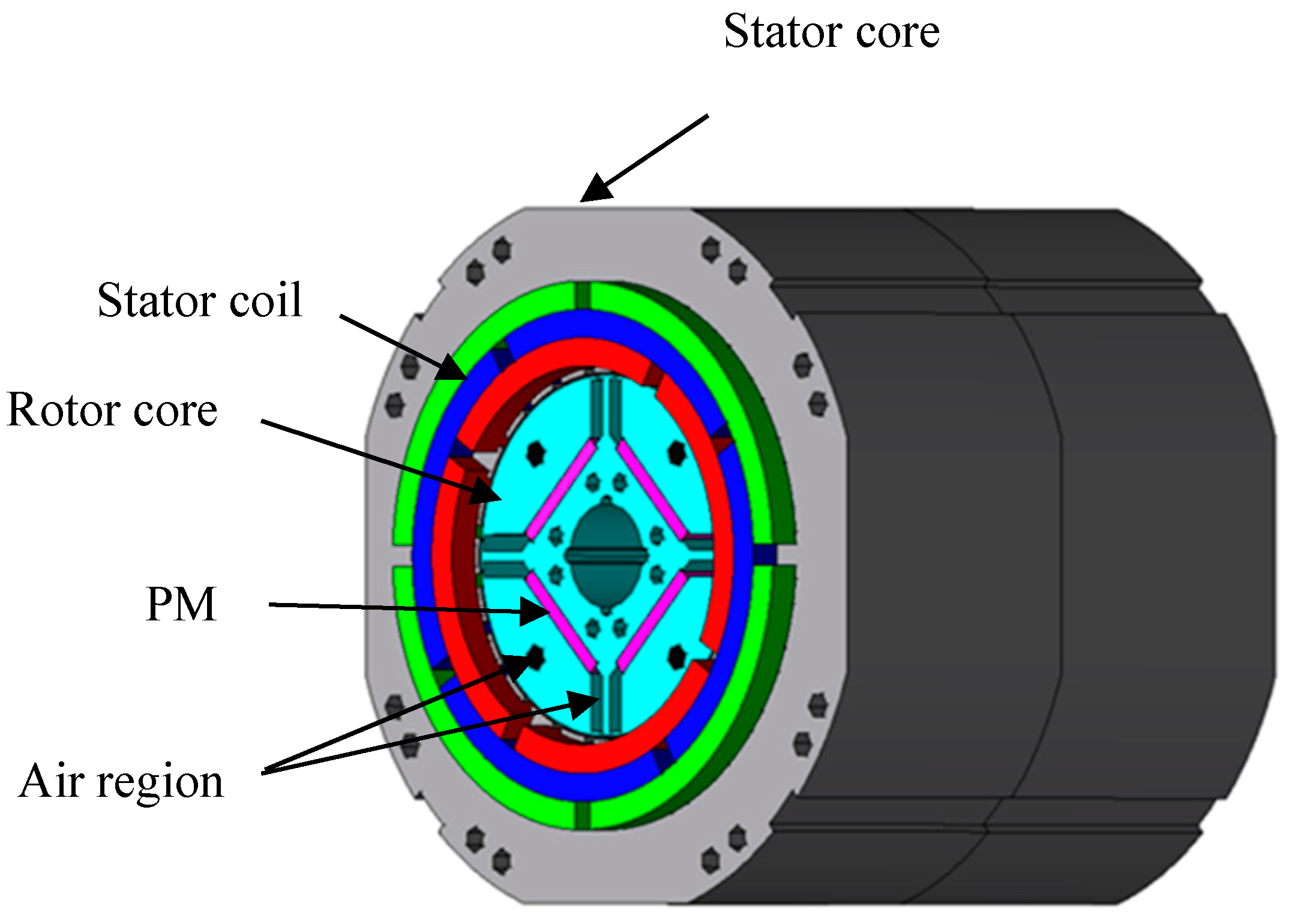
2. Experimental PMSM with Demagnetization
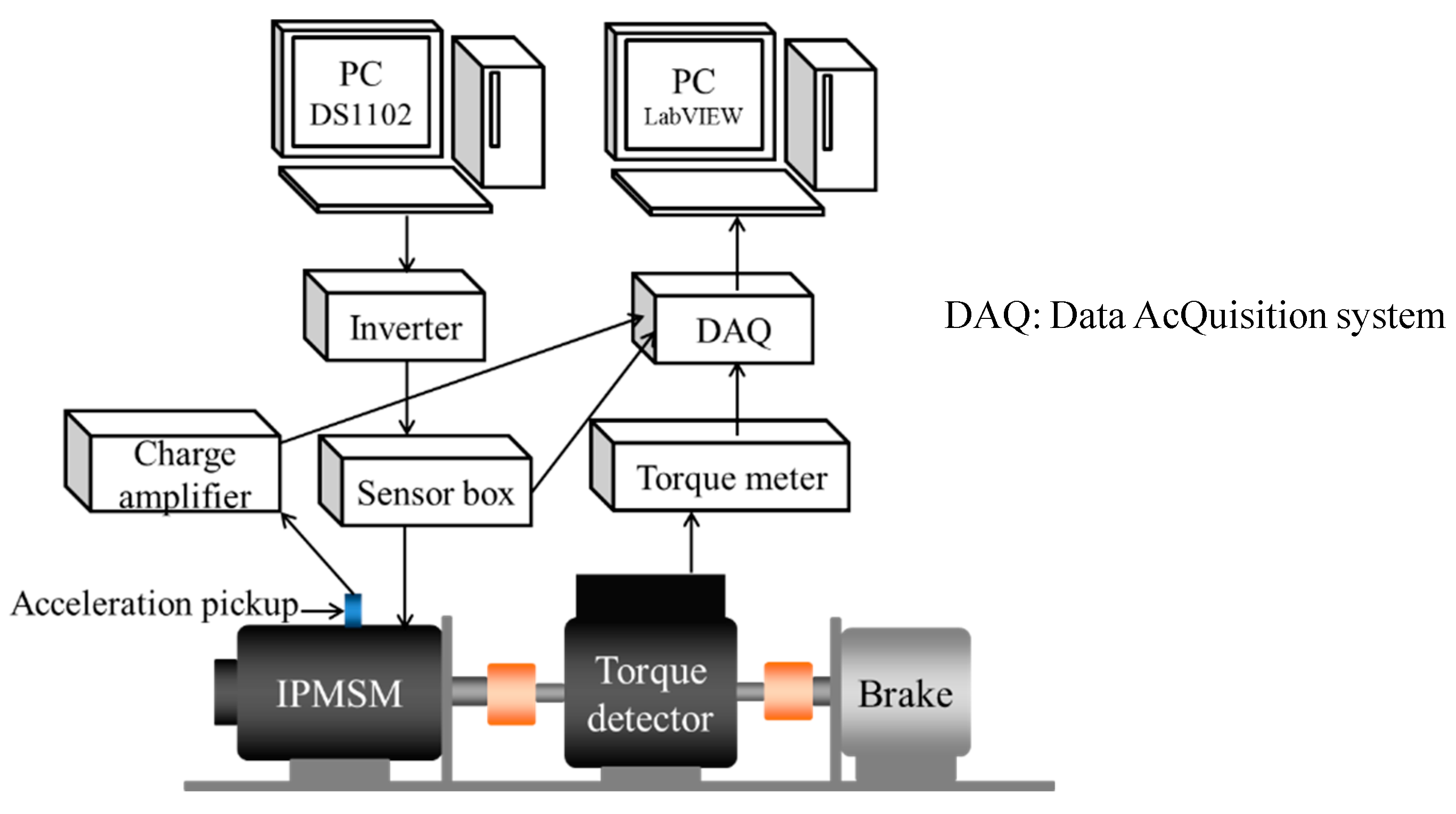
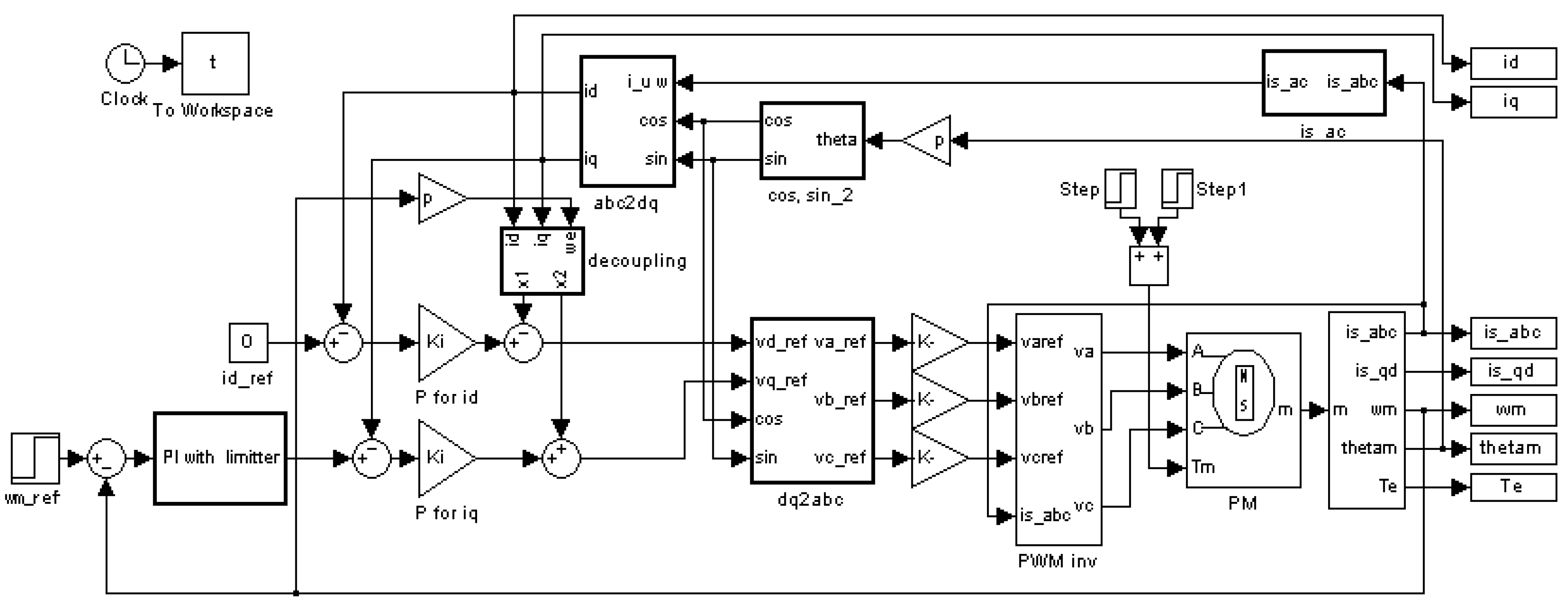
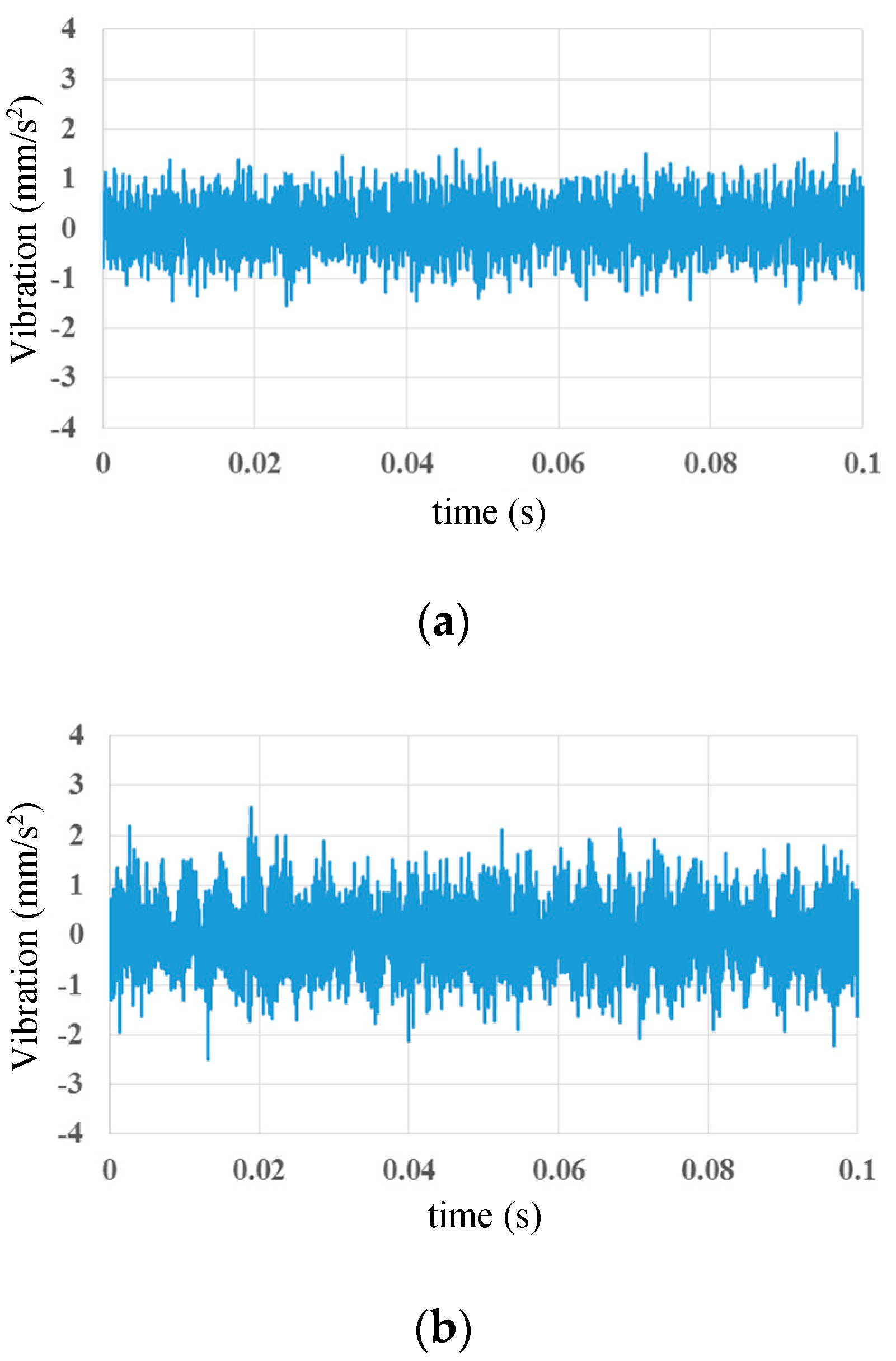
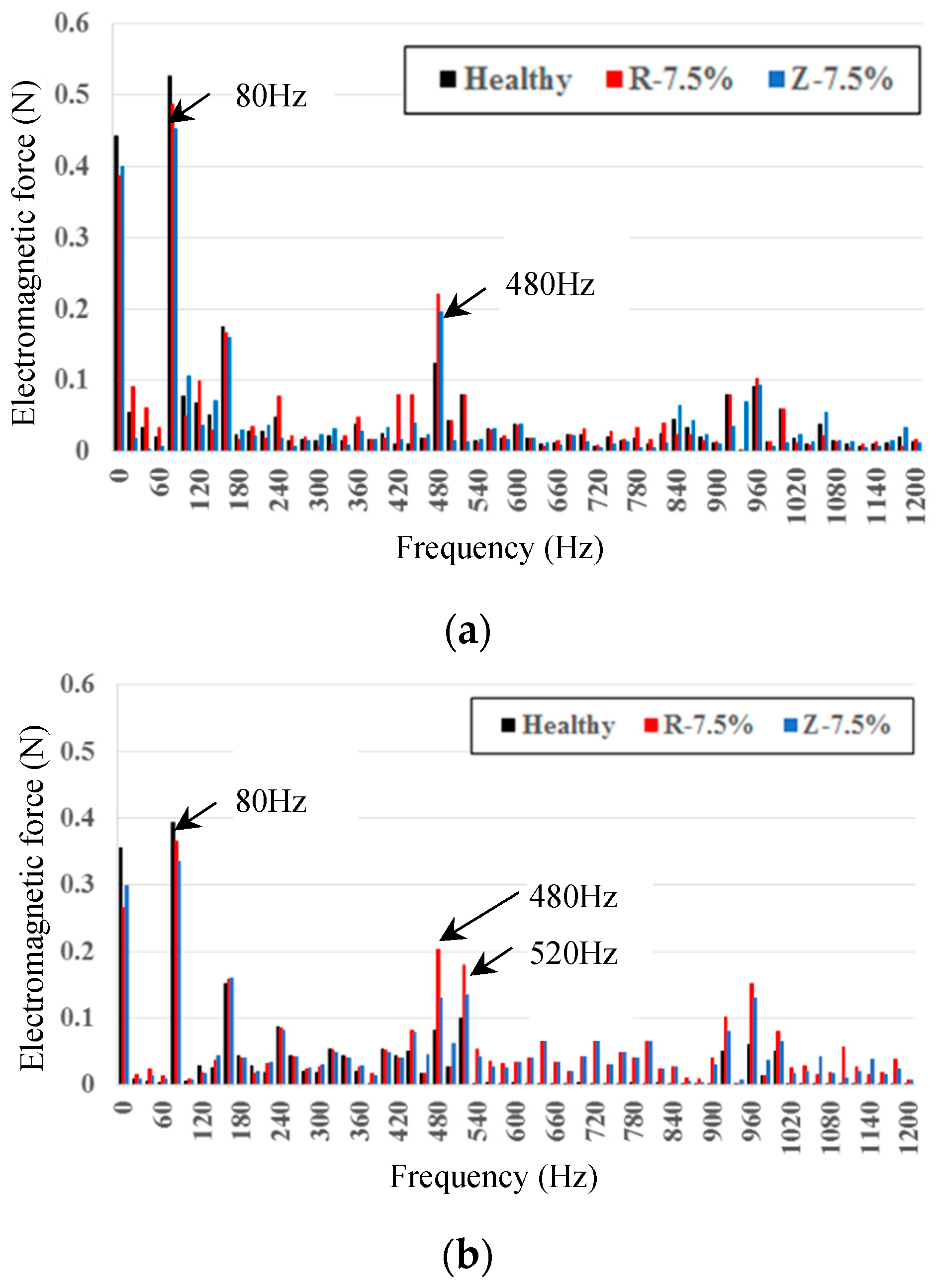
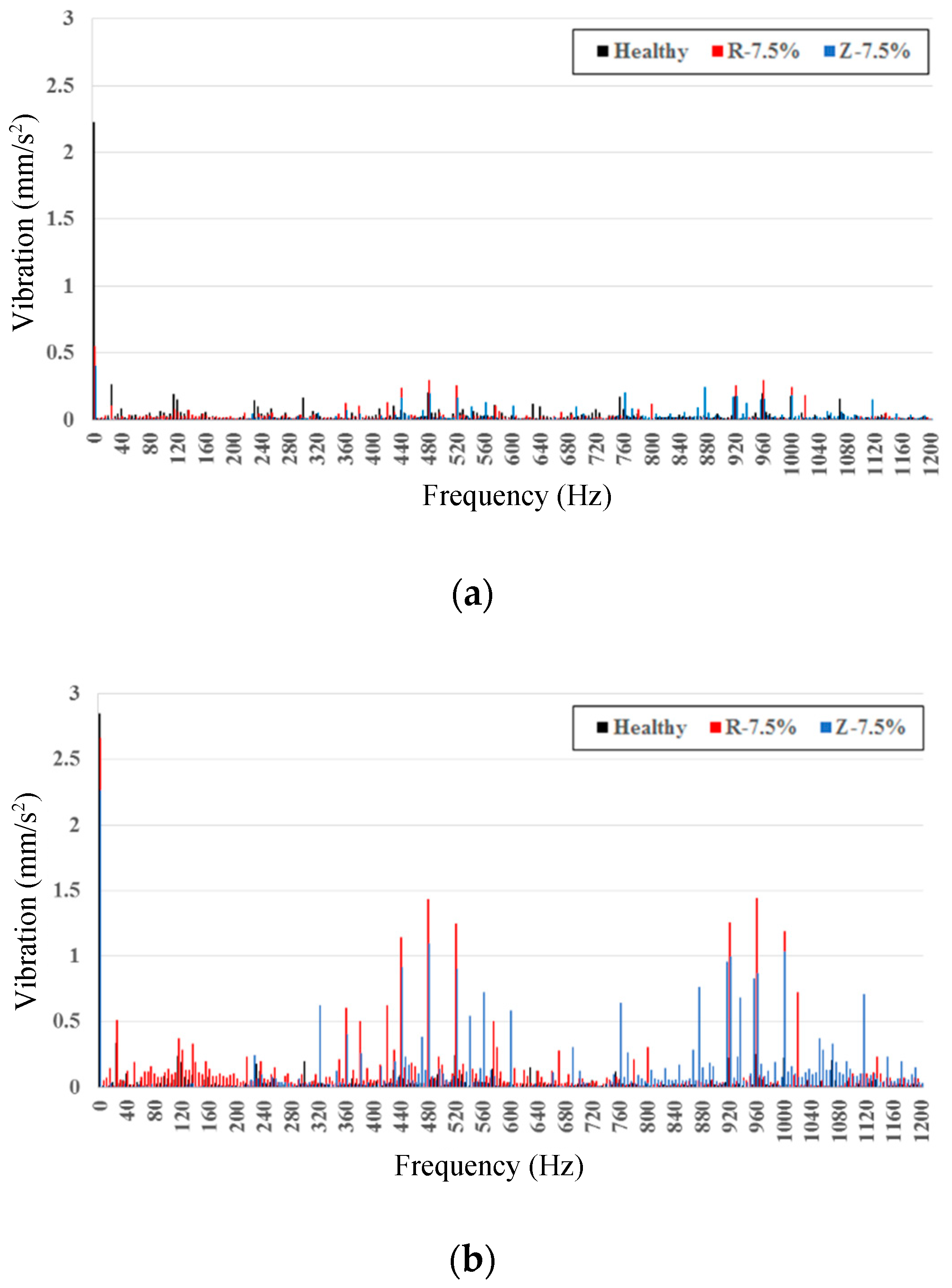
3. Vibration Characteristics of an Experimental IPMSM Driven under Vector Control
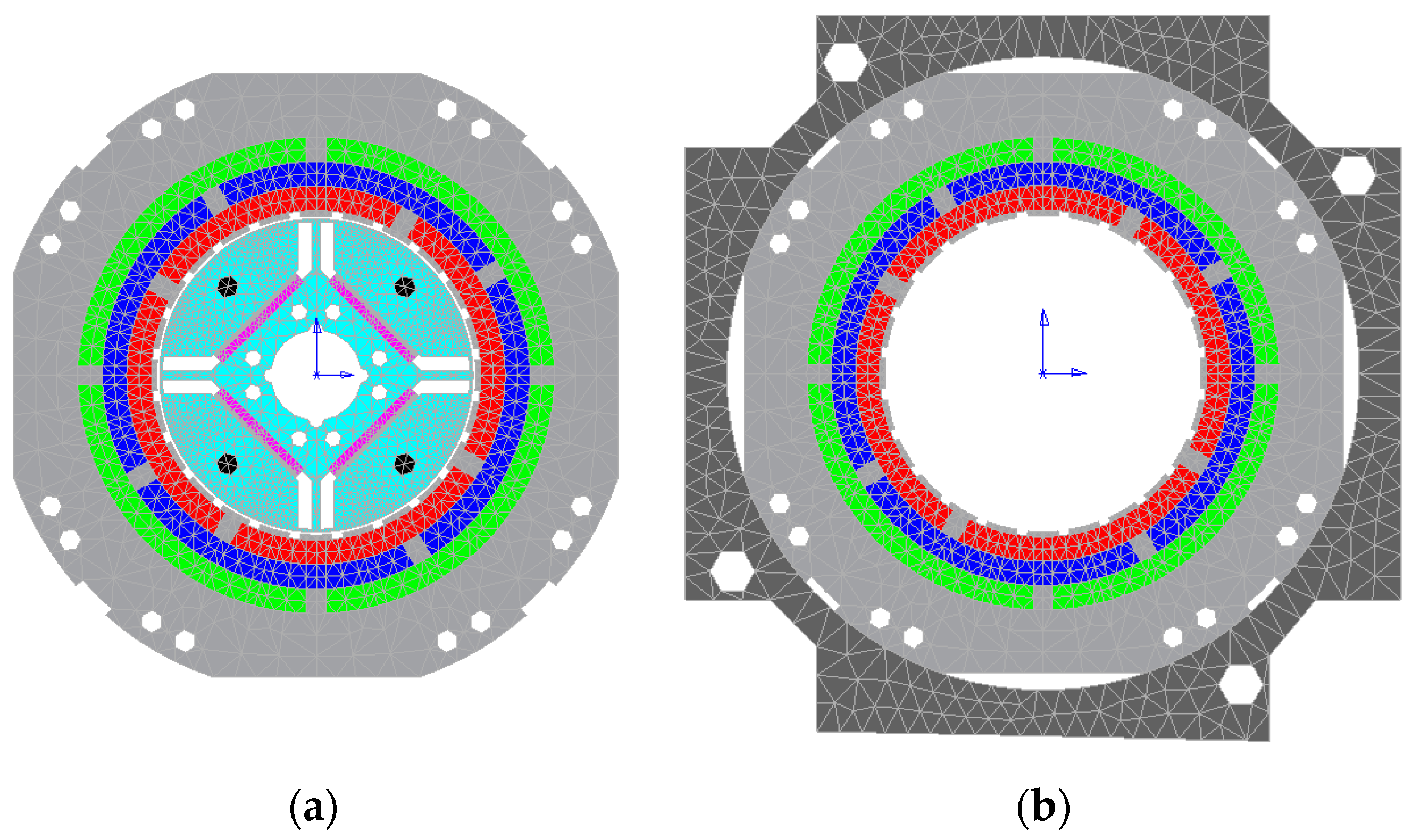
4. 3-D FE Analysis of Vibration Characteristics
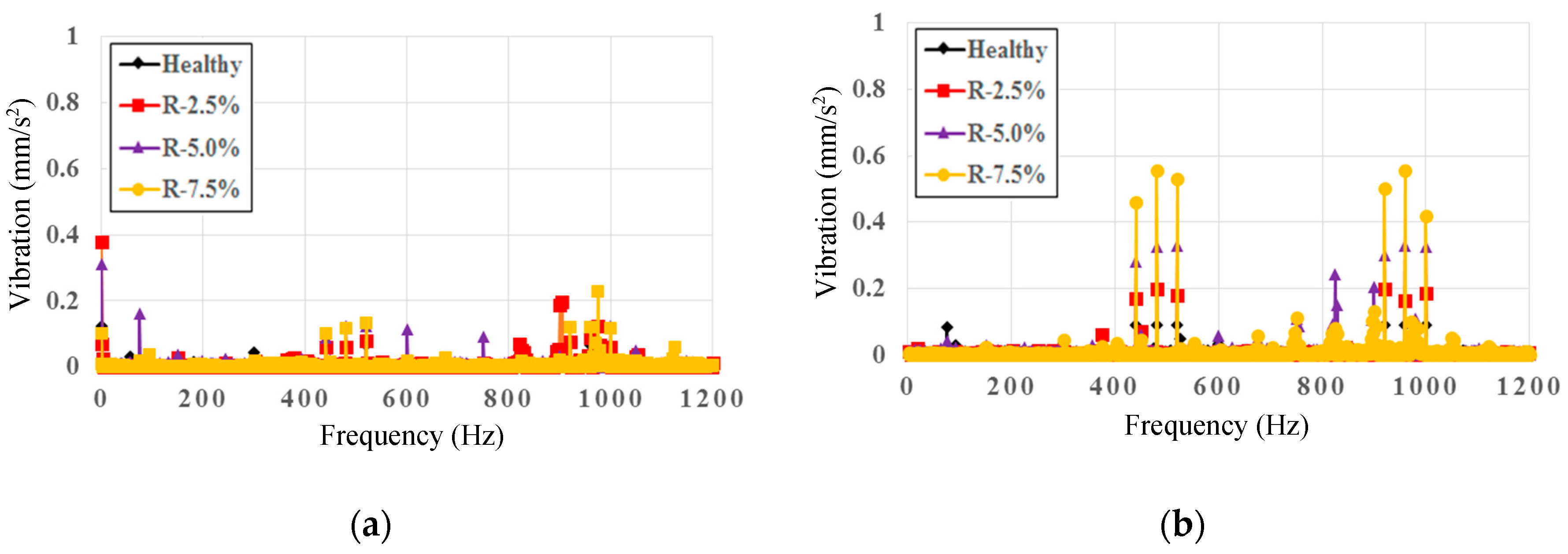
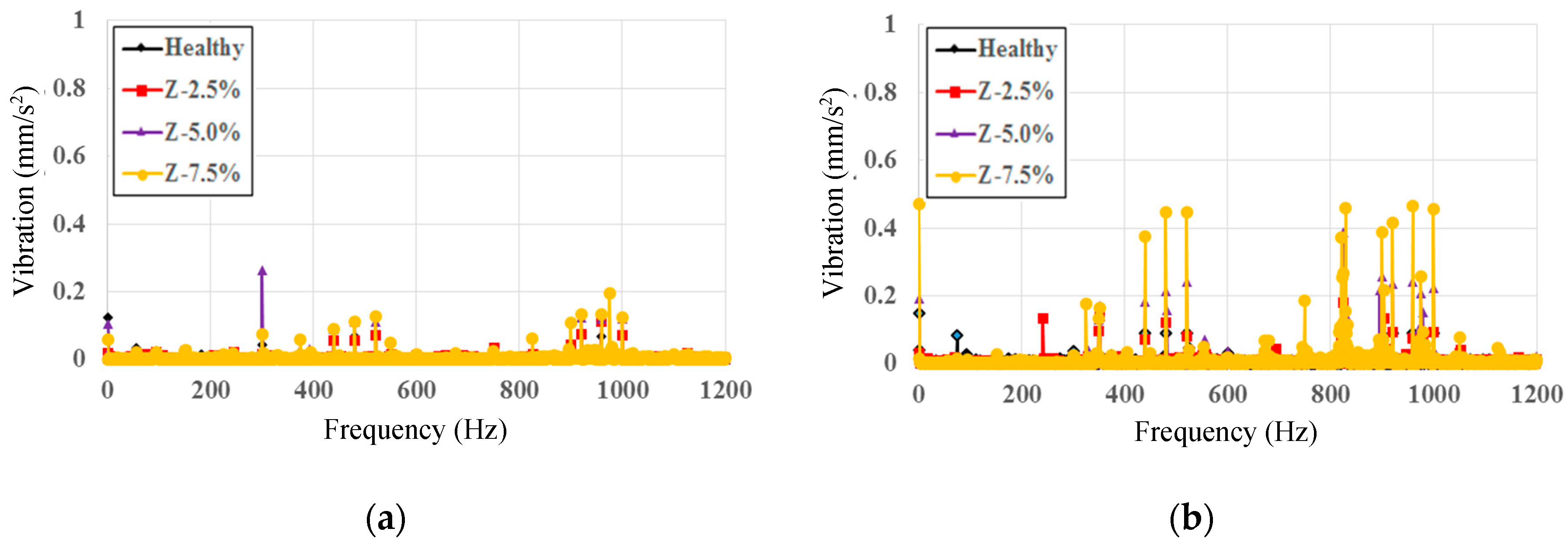
5. Estimation of Demagnetization Level
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Y.; Liang, S.; Li, W.; Liang, H.; Wang, C. Faults and Diagnosis Methods of Permanent Magnet Synchronous Motors: A Review. Appl. Sci. 2019, 9, 2116. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J.; Huiping, Y.; Zhou, W. A review of Permanent Magnet Synchronous Motor fault diagnosis. In Proceedings of the IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar]
- Singh, S.; Kumar, N. Detection of Bearing Faults in Mechanical Systems Using Stator Current Monitoring. IEEE Trans. Ind. Inform. 2017, 13, 1341–1349. [Google Scholar] [CrossRef]
- Nayana, B.R.; Geethanjali, P. Analysis of Statistical Time-Domain Features Effectiveness in Identification of Bearing Faults from Vibration Signal. IEEE Sens. J. 2017, 17, 5618–5625. [Google Scholar] [CrossRef]
- Razavi-Far, R.; Farajzadeh-Zanjani, M.; Saif, M. An Integrated Class-Imbalanced Learning Scheme for Diagnosing Bearing Defects in Induction Motors. IEEE Trans. Ind. Inf. 2017, 13, 2758–2769. [Google Scholar] [CrossRef]
- Helmi, H.; Forouzantabar, A. Rolling bearing fault detection of electric motor using time domain and frequency domain features extraction and ANFIS. IET Electr. Power Appl. 2019, 13, 662–669. [Google Scholar] [CrossRef]
- Lopez-Perez, D.; Antonino-Daviu, J. Application of Infrared Thermography to Failure Detection in Industrial Induction Motors: Case Stories. IEEE Trans. Ind. Appl. 2017, 53, 1901–1908. [Google Scholar] [CrossRef]
- Rahman, M.M.; Uddin, M.N. Online Unbalanced Rotor Fault Detection of an IM Drive Based on Both Time and Frequency Domain Analyses. IEEE Trans. Ind. Appl. 2017, 53, 4087–4096. [Google Scholar] [CrossRef]
- Ghosh, E.; Mollaeian, A.; Kim, S.; Tjong, J.; Kar, N.C. DNN-Based Predictive Magnetic Flux Reference for Harmonic Compensation Control in Magnetically Unbalanced Induction Motor. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Morales-Perez, C.; Rangel-Magdaleno, J.; Peregrina-Barreto, H.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M. Incipient Broken Rotor Bar Detection in Induction Motors Using Vibration Signals and the Orthogonal Matching Pursuit Algorithm. IEEE Trans. Instrum. Meas. 2018, 67, 2058–2068. [Google Scholar] [CrossRef]
- Ali, M.Z.; Shabbir, M.N.S.K.; Liang, X.; Zhang, Y.; Hu, T. Machine Learning-Based Fault Diagnosis for Single- and Multi-Faults in Induction Motors Using Measured Stator Currents and Vibration Signals. IEEE Trans. Ind. Appl. 2019, 55, 2378–2391. [Google Scholar] [CrossRef]
- Barusu, M.R.; Sethurajan, U.; Deivasigamani, M. Non-invasive method for rotor bar fault diagnosis in three-phase squirrel cage induction motor with advanced signal processing technique. J. Eng. 2019, 2019, 4415–4419. [Google Scholar] [CrossRef]
- Glowacz, A. Fault diagnosis of single-phase induction motor based on acoustic signals. Mech. Syst. Signal Process. 2019, 117, 65–80. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, W. Vibration-Based Fault Diagnosis of Commutator Motor. Shock Vib. 2018, 2018. [Google Scholar] [CrossRef]
- Glowacz, A. Fault Detection of Electric Impact Drills and Coffee Grinders Using Acoustic Signals. Sensors 2019, 19, 269. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Zuo, S.; Cao, J. Effects of Rotor Position Error on Longitudinal Vibration of Electric Wheel System in In-Wheel PMSM Driven Vehicle. IEEE/ASME Trans. Mechatron. 2018, 23, 1314–1325. [Google Scholar] [CrossRef]
- Cuevas, M.; Romary, R.; Lecointe, J.; Morganti, F.; Jacq, T. Noninvasive Detection of Winding Short-Circuit Faults in Salient Pole Synchronous Machine With Squirrel-Cage Damper. IEEE Trans. Ind. Appl. 2018, 54, 5988–5997. [Google Scholar] [CrossRef]
- Park, Y.; Fernandez, D.; Lee, S.B.; Hyun, D.; Jeong, M.; Kommuri, S.K.; Briz, F. Online Detection of Rotor Eccentricity and Demagnetization Faults in PMSMs Based on Hall-Effect Field Sensor Measurements. IEEE Trans. Ind. Appl. 2019, 55, 2499–2509. [Google Scholar] [CrossRef]
- Cheng, M.; Gao, F.; Li, Y. Vibration Detection and Experiment of PMSM High Speed Grinding Motorized Spindle Based on Frequency Domain Technology. Meas. Sci. Rev. 2019, 19, 109–125. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Edwardo FFukushima, S.J.; Zhang, C.; He, J. Estimation of Sensor Faults and Unknown Disturbance in Current Measurement Circuits for PMSM Drive System. Measurement 2019, 137, 580–587. [Google Scholar] [CrossRef]
- Faiz, J.; Koti, H.N. Demagnetization Fault Indexes in Permanent Magnet Synchronous Motors. An Overview. IEEE Trans. Magn. 2016, 52, 8201511. [Google Scholar] [CrossRef]
- Rajagopalan, S.; Le, R.; Habetler, T.; Harley, R. Diagnosis of potential rotor faults in brushless DC machines. Proc. Inst. Elect. Eng. Conf. Publ. 2004, 2, 668–673. [Google Scholar]
- Urresty, J.; Riba, J.; Delgado, M.; Romeral, L. Detection of Demagnetization Faults in Surface-Mounted Permanent Magnet Synchronous Motors by Means of the Zero-Sequence Voltage Component. IEEE Trans. Energy Convers. 2012, 27, 42–51. [Google Scholar] [CrossRef]
- Torregrossa, D.; Khoobroo, A.; Fahimi, B. Prediction of Acoustic Noise and Torque Pulsation in PM Synchronous Machines with Static Eccentricity and Partial Demagnetization Using Field Reconstruction Method. IEEE Trans. Ind. Electron. 2012, 59, 934–944. [Google Scholar] [CrossRef]
- Liu, K.; Zhu, Z. Online Estimation of the Rotor Flux Linkage and Voltage-Source Inverter Nonlinearity in Permanent Magnet Synchronous Machine Drives. IEEE Trans. Power Electron. 2014, 29, 418–427. [Google Scholar] [CrossRef]
- Yang, Z.; Shi, X.; Krishnamurthy, M. Vibration monitoring of PM synchronous machine with partial demagnetization and inter-turn short circuit faults. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo, Dearborn, MI, USA, 15–18 June 2014. [Google Scholar]
- Alameh, K.; Cite, N.; Hoblos, G.; Barakat, G. Vibration-based Fault Diagnosis Approach for Permanent Magnet Synchronous Motors. IFAC Pap. 2015, 48, 1444–1450. [Google Scholar] [CrossRef]
- Zhu, M.; Hu, W.; Kar, N.C. Torque-Ripple-Based Interior Permanent-Magnet Synchronous Machine Rotor Demagnetization Fault Detection and Current Regulation. IEEE Trans. Ind. Appl. 2017, 53, 2795–2804. [Google Scholar] [CrossRef]
- Wallscheid, O.; Huber, T.; Peters, W.; Bocker, J. Real-Time Capable Methods to Determine the Magnet Temperature of Permanent Magnet Synchronous Motors—A Review. In Proceedings of the IEEE-IECON, Dallas, TX, USA, 29 October–1 November 2014; pp. 811–818. [Google Scholar]
- Shinagawa, S.; Ishikawa, T.; Kurita, N. Characteristics of Interior Permanent Magnet Synchronous Motor with Imperfect Magnets. IEEJ J. Ind. Appl. 2015, 4, 346–351. [Google Scholar] [CrossRef] [Green Version]
- Ishikawa, T.; Igarashi, N.; Kurita, N. Failure Diagnosis for Demagnetization in Interior Permanent Magnet Synchronous Motors. Int. J. Rotating Mach. 2017, 2017. [Google Scholar] [CrossRef]



| PM | L (mm) | W (mm) | H (mm) | V (mm3) | V/VHealthy |
|---|---|---|---|---|---|
| Healthy | 22.6 | 20.2 | 2.2 | 16070 | - |
| R-2.5% | 22.6 | 20.2 | 2.0 | 15704 | 0.977 |
| R-5.0% | 22.6 | 20.2 | 1.8 | 15339 | 0.955 |
| R-7.5% | 22.6 | 20.2 | 1.6 | 14974 | 0.932 |
| Z-2.5% | 18.0 | 20.2 | 2.2 | 15661 | 0.975 |
| Z-5.0% | 13.4 | 20.2 | 2.2 | 15252 | 0.950 |
| Z-7.5% | 8.8 | 20.2 | 2.2 | 14843 | 0.924 |
| Measured (Hz) | Calculated (Hz) | Relative Error (%) |
|---|---|---|
| 179 | 207 | 15.6 |
| 472 | 521 | 12.5 |
| 592 | 647 | 11.0 |
| 952 | 1063 | 11.8 |
| 1240 | 1371 | 11.1 |
| 1468 | 1655 | 12.7 |
| Vibration (mm/s2) | ||||
|---|---|---|---|---|
| Frequency (Hz) | Condition | Healthy | R-7.5% | Z-7.5% |
| 440 (11th) | No load | 0.070 | 0.235 | 0.162 |
| 480 (12th) | No load | 0.205 | 0.294 | 0.194 |
| 520 (13th) | No load | 0.192 | 0.256 | 0.160 |
| 920 (23rd) | No load | 0.173 | 0.257 | 0.176 |
| 960 (24th) | No load | 0.197 | 0.297 | 0.153 |
| 1000 (25th) | No load | 0.177 | 0.244 | 0.183 |
| 440 (11th) | 70% load | 0.090 | 1.14 | 0.915 |
| 480 (12th) | 70% load | 0.263 | 1.43 | 1.10 |
| 520 (13th) | 70% load | 0.245 | 1.25 | 0.903 |
| 920 (23rd) | 70% load | 0.221 | 1.25 | 0.997 |
| 960 (24th) | 70% load | 0.252 | 1.44 | 0.866 |
| 1000 (25th) | 70% load | 0.226 | 1.19 | 1.03 |
| 207 (1st eigenvalue) | 70% load | 0.006 | 0.008 | 0.001 |
| 472 (2nd eigenvalue) | 70% load | 0.022 | 0.007 | 0.068 |
| 593 (3rd eigenvalue) | 70% load | 0.022 | 0.009 | 0.001 |
| 952 (4th eigenvalue) | 70% load | 0.051 | 0.18 | 0.018 |
| Torque (Nm) | Vibration (mm/s2) | Estimated Value (%) |
|---|---|---|
| 0.0 | 0.067 | −0.80 |
| 0.48 | 0.093 | −3.21 |
| 0.95 | 0.139 | −4.06 |
| 1.43 | 0.166 | −3.59 |
| 1.91 | 0.226 | −3.86 |
| 2.39 | 0.267 | −3.70 |
| 2.86 | 0.324 | −3.46 |
| 3.34 | 0.396 | −3.51 |
| Torque (Nm) | Vibration (mm/s2) | Estimated Value (%) |
|---|---|---|
| 0.0 | 0.071 | +1.12 |
| 0.48 | 0.086 | −3.04 |
| 0.95 | 0.115 | −3.20 |
| 1.43 | 0.134 | −3.59 |
| 1.91 | 0.159 | −3.36 |
| 2.39 | 0.179 | −3.34 |
| 2.86 | 0.211 | −3.41 |
| 3.34 | 0.234 | −3.52 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishikawa, T.; Igarashi, N. Failure Diagnosis of Demagnetization in Interior Permanent Magnet Synchronous Motors Using Vibration Characteristics. Appl. Sci. 2019, 9, 3111. https://doi.org/10.3390/app9153111
Ishikawa T, Igarashi N. Failure Diagnosis of Demagnetization in Interior Permanent Magnet Synchronous Motors Using Vibration Characteristics. Applied Sciences. 2019; 9(15):3111. https://doi.org/10.3390/app9153111
Chicago/Turabian StyleIshikawa, Takeo, and Naoto Igarashi. 2019. "Failure Diagnosis of Demagnetization in Interior Permanent Magnet Synchronous Motors Using Vibration Characteristics" Applied Sciences 9, no. 15: 3111. https://doi.org/10.3390/app9153111
APA StyleIshikawa, T., & Igarashi, N. (2019). Failure Diagnosis of Demagnetization in Interior Permanent Magnet Synchronous Motors Using Vibration Characteristics. Applied Sciences, 9(15), 3111. https://doi.org/10.3390/app9153111




