Integration of Reversible Heat Pumps in Trigeneration Systems for Low-Temperature Renewable District Heating and Cooling Microgrids
Abstract
:1. Introduction
2. Methodology
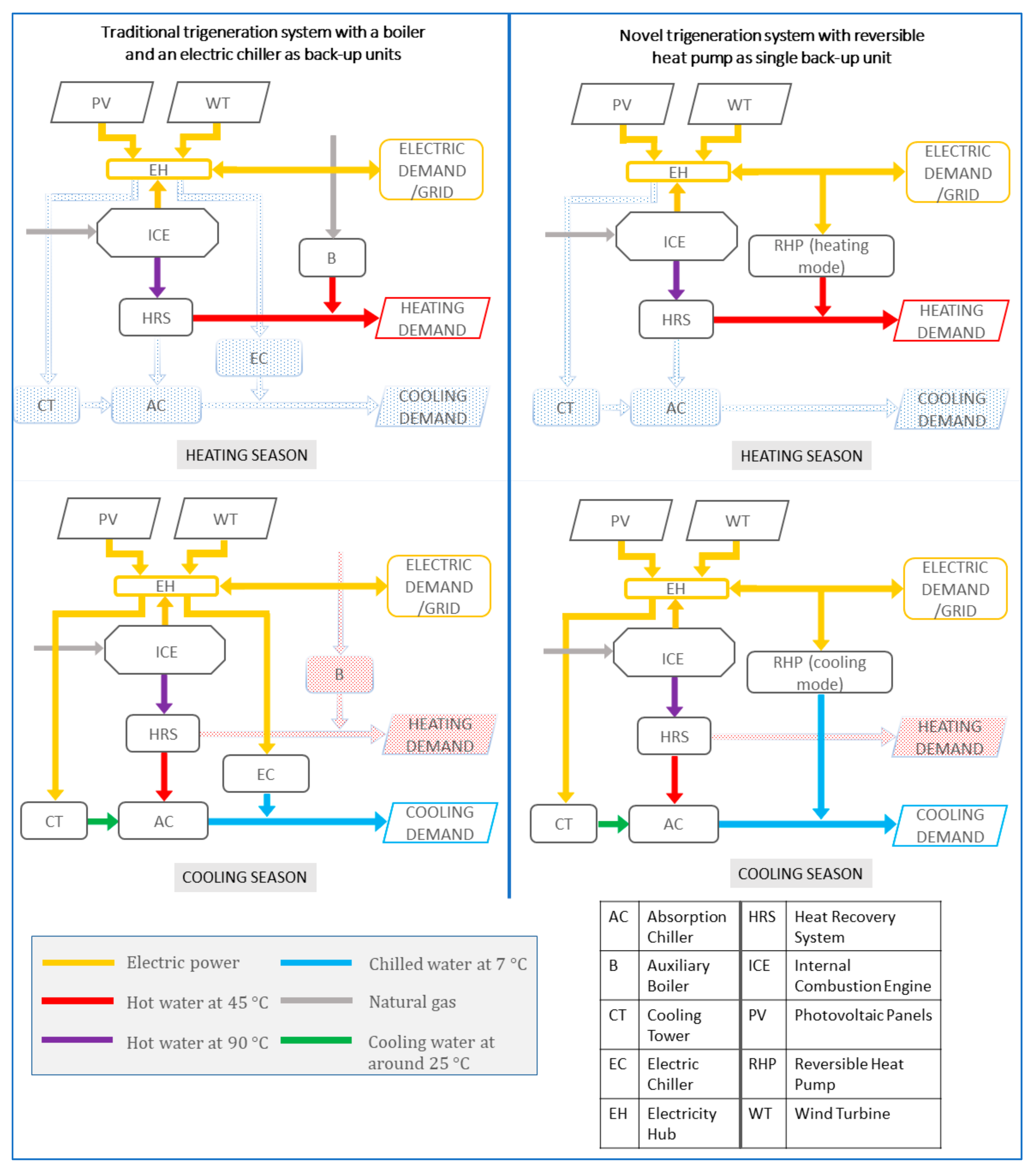
2.1. The Energy System
2.2. Subsystem Models
2.3. Optimization Problem and Method
3. Case Study: Energy Demand and Economic Parameters
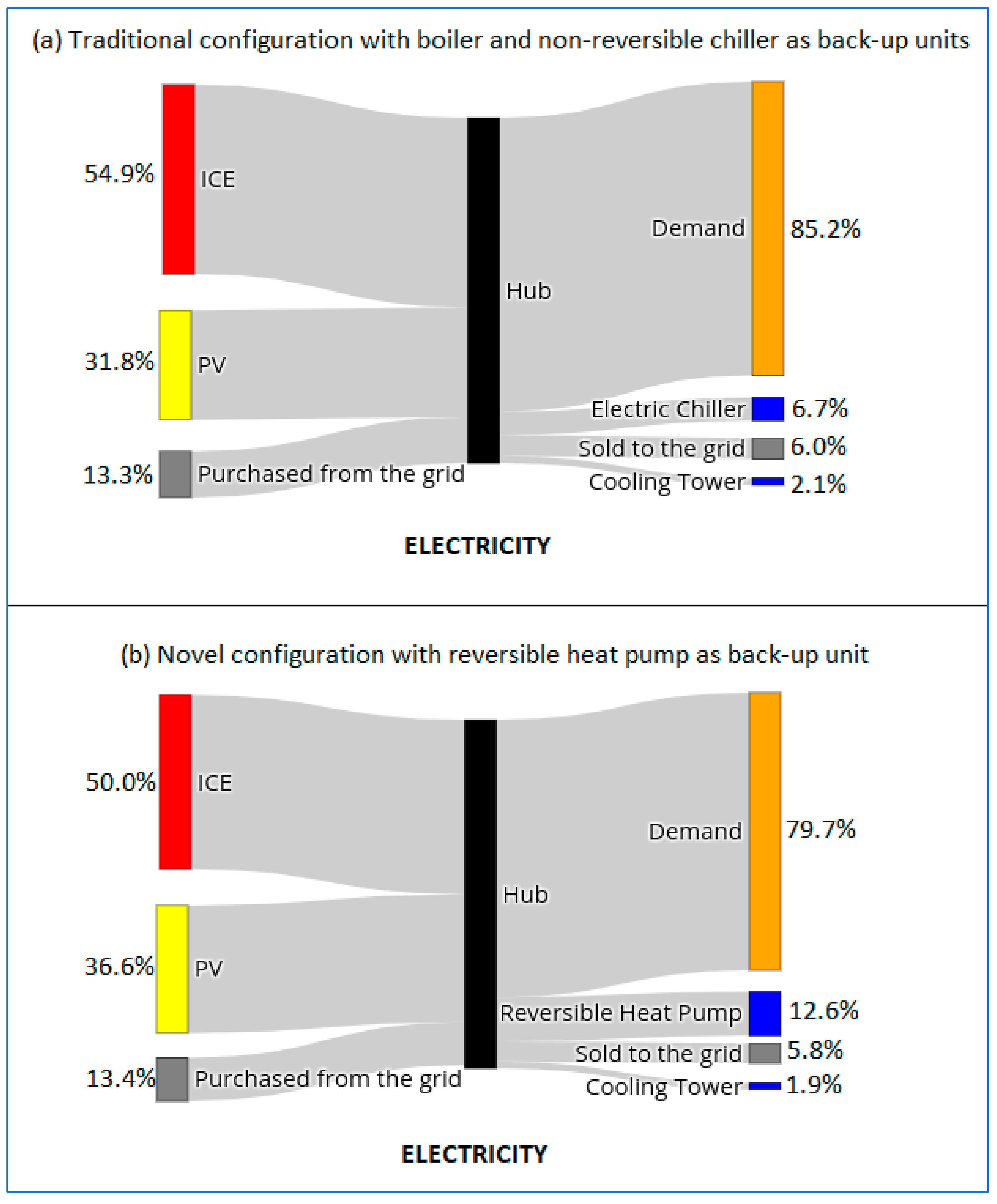
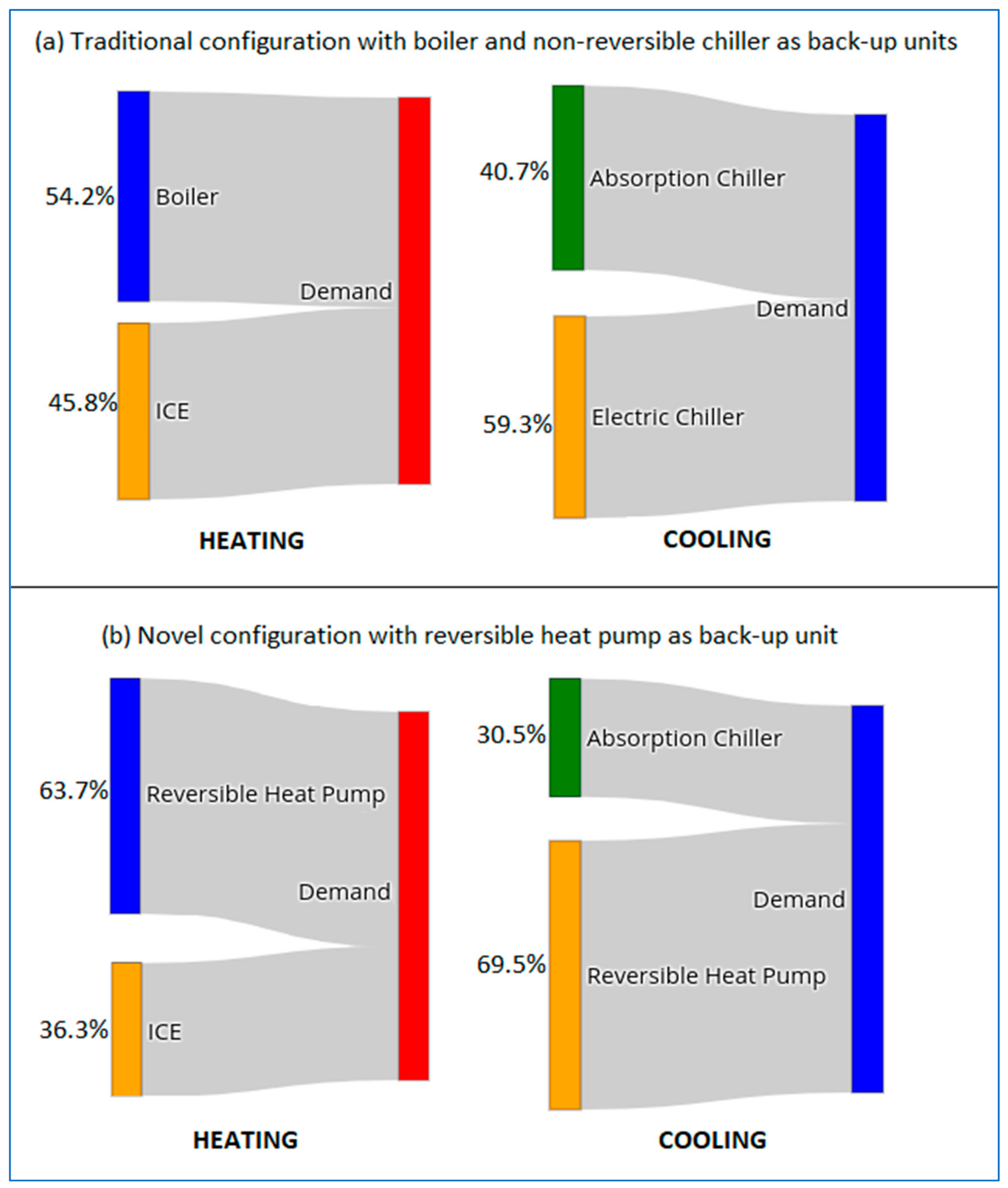
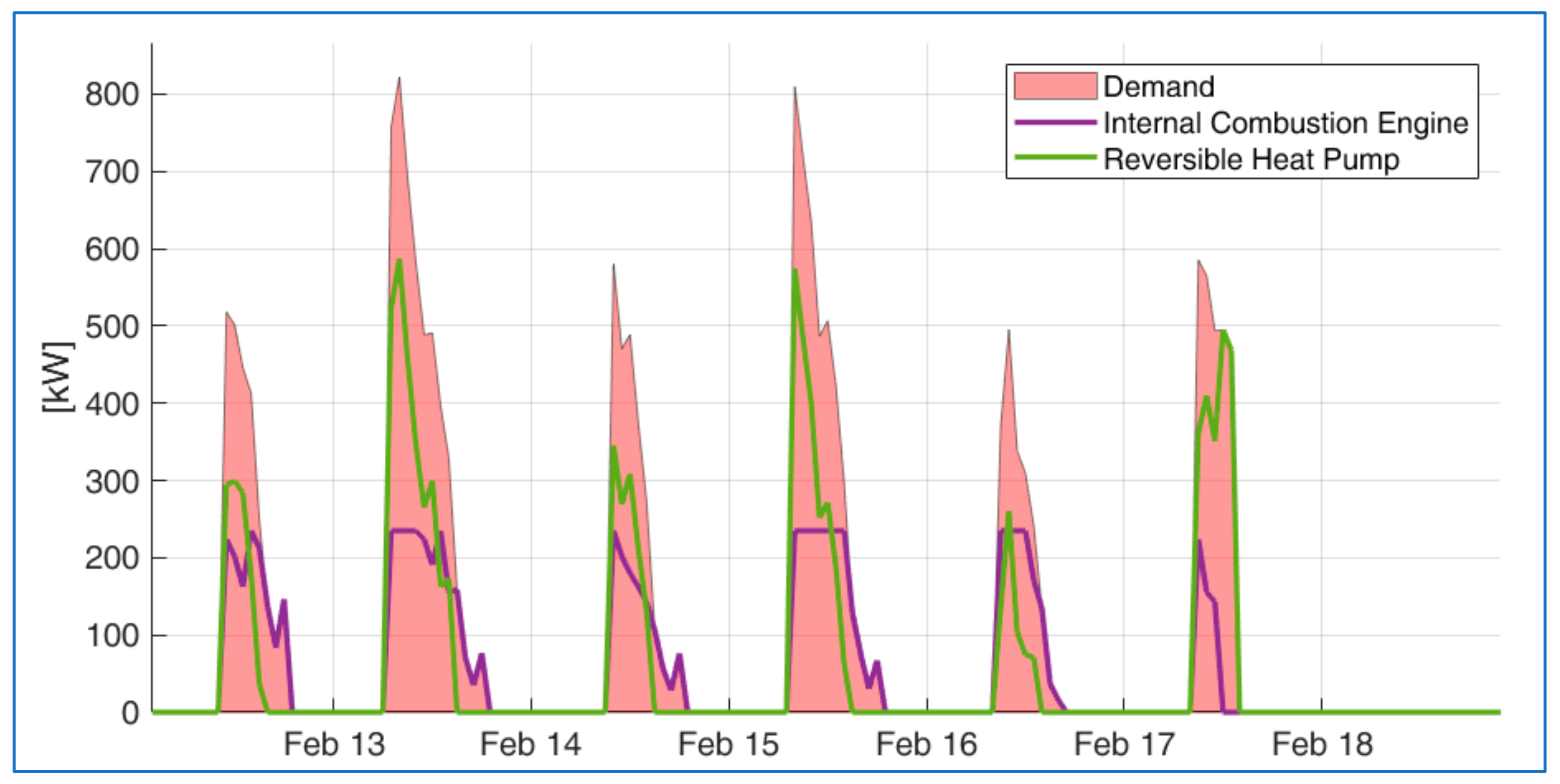
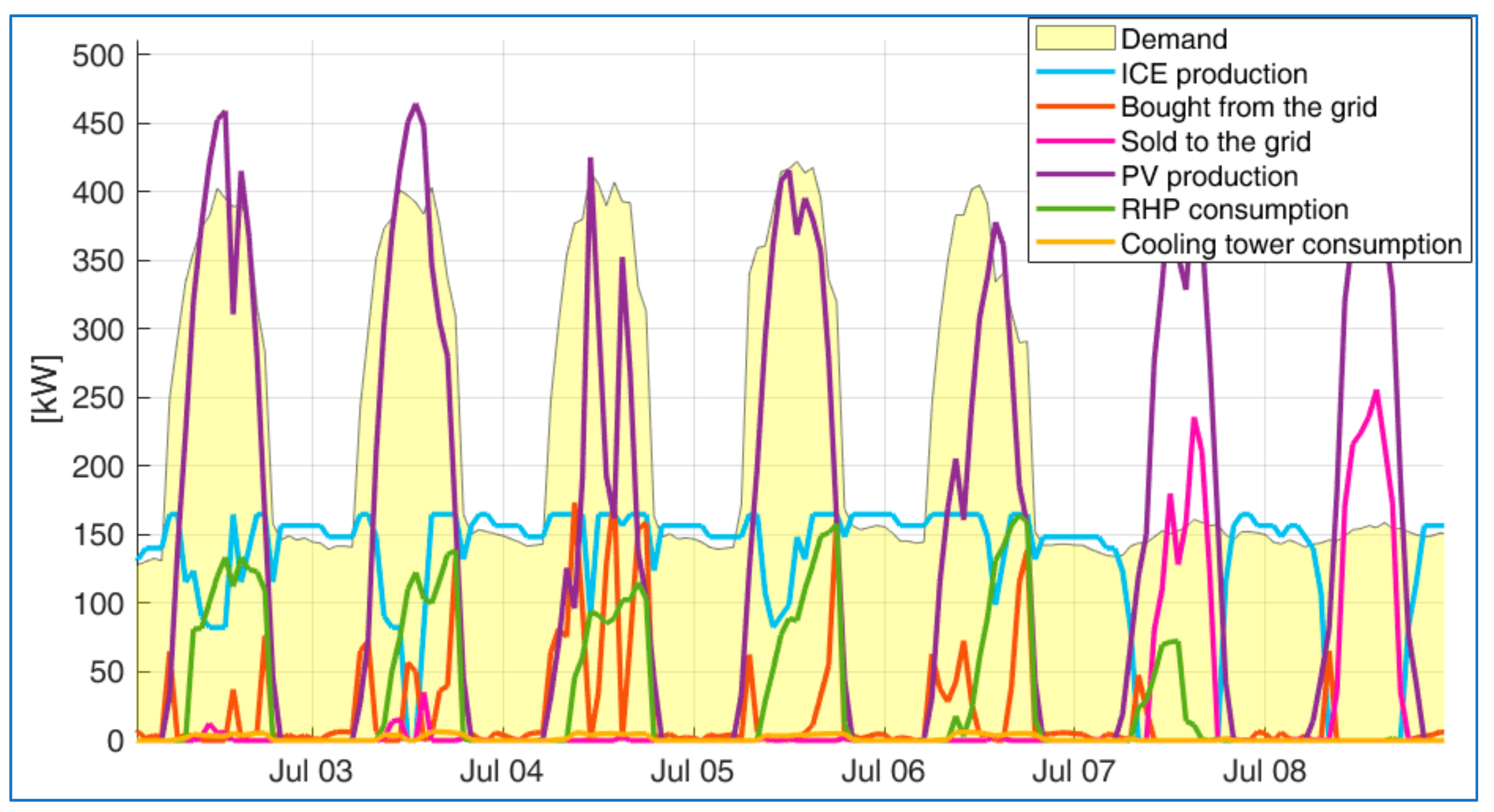
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Acronyms | |
| 4GDH | 4th Generation District Heating |
| DHC | District Heating and Cooling |
| GA | Genetic Algorithm |
| NOCT | Nominal Operating Cell Temperature |
| RES | Renewable Energy Source |
| STC | Standard Test Conditions |
| Parameters | |
| a | Coefficient of the equipment cost curve, €/kW |
| b | Exponent of the equipment cost curve, dimensionless |
| c | Cost per unit of energy, €/kWh |
| CAP | Capacity, kW |
| CF | Correction factor, dimensionless |
| COP | Coefficient of performance, dimensionless |
| CRF | Capital recovery factor, dimensionless |
| EAC | Equivalent annual cost, € |
| Invest | Investment cost, € |
| k | Weibull shape parameter, dimensionless |
| Op | Annual operating cost, € |
| r | Interest rate, dimensionless |
| SCOP | Seasonal coefficient of performance, dimensionless |
| t | Timestep, hour |
| z | Height, m |
| PV power temperature coefficient, °C−1 | |
| Electric energy consumption per unit of rejected heat, dimensionless | |
| Efficiency, dimensionless | |
| Heat pump capacity temperature coefficient, kW/°C | |
| Continuous variables | |
| C | Cooling power, kW |
| E | Electric power, kW |
| G | Solar irradiance, kW/m2 |
| L | Load factor (defined as the ratio between the power output of the unit and its capacity), dimensionless |
| v | Wind speed, m/s |
| Q | Heating power, kW |
| T | Temperature, °C |
| Thermal energy, kWh | |
| Binary variables | |
| On-off state | |
| Subscripts | |
| AC | Absorption chiller |
| B | Boiler |
| C | Cooling mode |
| CT | Cooling Tower |
| D | Demand |
| E | Electric energy |
| EC | Electric chiller |
| ex | Exergy |
| F | Fuel |
| gen | Generator |
| H | Heating mode |
| ICE | Internal Combustion Engine |
| nom | Nominal |
| P | Purchased from the grid |
| PV | PhotoVoltaics |
| RHP | Reversible Heat Pump |
| S | Sold to the grid |
| WT | Wind Turbine |
References
- International Energy Agency (IEA). Global Energy and CO2 Status Report 2018. Available online: https://www.iea.org/geco (accessed on 5 August 2019).
- Lund, H.; Østergaard, P.A.; Connolly, D.; Mathiesen, B.V. Smart energy and smart energy systems. Energy 2017, 137, 556–565. [Google Scholar] [CrossRef]
- Karmellos, M.; Georgiou, P.N.; Mavrotas, G. A comparison of methods for the optimal design of Dsitrbuted Energy Systems under uncertainty. Energy 2019, 178, 318–333. [Google Scholar] [CrossRef]
- Werner, S. International review of district heating and cooling. Energy 2017, 137, 617–631. [Google Scholar] [CrossRef]
- Buffa, S.; Cozzini, M.; D’Antoni, M.; Baratieri, M.; Fedrizzi, R. 5th generation district heating and cooling systems: A review of existing cases in Europe. Renew. Sustain. Energy Rev. 2019, 104, 504–522. [Google Scholar] [CrossRef]
- Lund, H.; Werner, S.; Wiltshire, R.; Svendsen, S.; Thorsen, J.E.; Hvelpund, F.; Vad Mathiesen, B. 4th Generation District Heating (4GDH) Integrating smart thermal grids into future sustainable energy systems. Energy 2014, 68, 1–11. [Google Scholar] [CrossRef]
- Sameti, M.; Haghighat, F. Optimization of 4th generation distributed district heating system: Design and planning of combined heat and power. Renew. Energy 2019, 130, 371–387. [Google Scholar] [CrossRef]
- Cai, H.; You, S.; Wang, J.; Bindner, H.W.; Klyapovskiy, S. Technical assessment of electric heat boosters in low-temperature district heating based on combined heat and power analysis. Energy 2018, 150, 938–949. [Google Scholar] [CrossRef] [Green Version]
- Baldvinsson, I.; Nakata, T. A feasibility and performance assessment of a low temperature district heating system–a North Japanese case study. Energy 2016, 95, 155–174. [Google Scholar] [CrossRef]
- Sameti, M.; Haghighat, F. Optimization approaches in district heating and cooling thermal network. Energy Build. 2017, 140, 121–130. [Google Scholar] [CrossRef]
- Inayat, A.; Raza, M. District cooling system via renewable energy sources: A review. Renew. Sustain. Energy Rev. 2019, 107, 360–373. [Google Scholar] [CrossRef]
- Soltero, V.M.; Chacartegui, R.; Ortiz, C.; Lizana, J.; Quirosa, G. Biomass District Heating Systems Based on Agriculture Residues. Appl. Sci. 2018, 8, 476. [Google Scholar] [CrossRef]
- Testi, D.; Conti, P.; Schito, E.; Urbanucci, L.; D’Ettorre, F. Synthesis and Optimal Operation of Smart Microgrids Serving a Cluster of Buildings on a Campus with Centralized and Distributed Hybrid Renewable Energy Units. Energies 2019, 12, 745. [Google Scholar] [CrossRef]
- Kang, L.G.; Yang, J.H.; An, Q.S.; Deng, S.; Zhao, J.; Li, Z.L.; Wang, Y.Z. Complementary configuration and performance comparison of CCHP-ORC system with a ground source heat pump under different operation strategies. Energy Convers. Manag. 2017, 135, 244–255. [Google Scholar] [CrossRef]
- Ommen, T.S.; Markussen, W.B.; Elmegaard, B. Heat pumps in combined heat and power systems. Energy 2014, 76, 989–1000. [Google Scholar] [CrossRef]
- Sayegh, M.; Jadwiszczak, P.; Axcell, B.; Niemierka, E.; Brys, K.; Jouhara, H. Heat pump placement, connection and operational modes in European district heating. Energy Build. 2018, 166, 122–144. [Google Scholar] [CrossRef]
- Ostergaard, P.A.; Jantzen, J.; Marczinkowski, H.M.; Kristensen, M. Business and socioeconomic assessment of introducing heat pumps with heat storage in small-scale district heating systems. Renew. Energy 2019, 139, 904–914. [Google Scholar] [CrossRef]
- Urbanucci, L.; Testi, D.; Bruno, J. An operational optimization method for a complex polygeneration plant based on real-time measurements. Energy Convers. Manag. 2018, 170, 50–61. [Google Scholar] [CrossRef]
- Kinab, E.; Marchio, D.; Rivière, P.; Zoughaib, A. Reversible heat pump model for seasonal performance optimization. Energy Build. 2010, 42, 2269–2280. [Google Scholar] [CrossRef]
- Madonna, F.; Bazzocchi, F. Annual performances of reversible air-to-water heat pumps in small residential buildings. Energy Build. 2013, 65, 299–309. [Google Scholar] [CrossRef]
- Dongellini, M.; Naldi, C.; Morini, G.L. Sizing effects on the energy performance of reversible air-source heat pumps for office buildings. Appl. Therm. Eng. 2017, 114, 1073–1081. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Keshavarz, A. Combined Cooling, Heating and Power: Decision-Making, Design and Optimization; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Cinquini, F. Dimensionamento e Gestione Ottimizzati di Sistemi a Pompa di Calore Aria-Acqua per la Climatizzazione Annuale di Edifici Terziari. Master’s Thesis, University of Pisa, Pisa, Italy, 2018. [Google Scholar]
- Aermec. Heat Pumps and Chillers: Catalogue and Technical Documentation. Available online: https://support.aermec.com/default.asp (accessed on 5 August 2019).
- Galletti. Heat Pumps and Chillers: Catalogue and Technical Documentation. Available online: http://www.galletti.com/users/login-utente (accessed on 5 August 2019).
- Rossato. Heat Pumps and Chillers: Catalogue and Technical Documentation. Available online: https://www.rossatogroup.com/prodotti/pompe-di-calore/pompe-di-calore-aria-acqua.html (accessed on 5 August 2019).
- YORK. Heat Pumps and Chillers: Catalogue and Technical Documentation. Available online: https://www.johnsoncontrols.com/-/media/jci/global-capabilities/be/files/be_york_industrial_commercial_hvac_2018.pdf (accessed on 5 August 2019).
- European Committee for Standardization. Heating Systems in Buildings–Method for Calculation of System Energy Requirements and System Efficiencies—Part 4-2: Space Heating Generation Systems, Heat Pump Systems; EN 15316-4-2; CEN: Brussels, Belgium, 2017. [Google Scholar]
- DiPippo, R. Geothermal Power Generation: Developments and Innovation; Woodhead Publishing: Sawston/Cambrige, UK, 2016. [Google Scholar]
- Zhou, Z.; Liu, P.; Li, Z.; Pistikopoulos, E.N.; Georgiadis, M.C. Impacts of equipment off-design characteristics on the optimal design and operation of combined cooling, heating and power systems. Comput. Chem. Eng. 2013, 48, 40–47. [Google Scholar] [CrossRef]
- Riffonneau, Y.; Bacha, S.; Barruel, F.; Ploix, S. Optimal Power Flow Management for Grid Connected PV Systems with Batteries. IEEE Trans. Sustain. Energy 2011, 2, 309–320. [Google Scholar] [CrossRef]
- Borowy, B.S.; Salameh, Z.M. Optimum photovoltaic array size for a hybrid wind/PV system. IEEE Trans. Energy Convers. 1994, 9, 482–488. [Google Scholar] [CrossRef]
- Abdmouleh, Z.; Gastli, A.; Ben-Brahim, L.; Haouari, M.; Al-Emadi, N.A. Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 2017, 113, 266–280. [Google Scholar] [CrossRef]
- Urbanucci, L.; Testi, D. Optimal integrated sizing and operation of a CHP system with Monte Carlo risk analysis for long-term uncertainty in energy demands. Energy Convers. Manag. 2018, 157, 307–316. [Google Scholar] [CrossRef]
- MATLAB. Genetic Algorithm Solver. Available online: https://it.mathworks.com/discovery/genetic-algorithm.html (accessed on 5 August 2019).
- Italian Thermotechnical Committee (CTI). National Typical Meteorological Years; CTI: Milan, Italy, 2016. [Google Scholar]
- Carvalho, M.; Lozano, M.A.; Ramos, J.; Serra, L.M. Synthesis of Trigeneration Systems: Sensitivity Analyses and Resilience. Sci. World J. 2013, 2013, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Urbanucci, L.; D’Ettorre, F.; Testi, D. A Comprehensive Methodology for the Integrated Optimal Sizing and Operation of Cogeneration Systems with Thermal Energy Storage. Energies 2019, 12, 875. [Google Scholar] [CrossRef]
- Renewable Energy Report, Politecnico di Milano. 2018. Available online: http://www.energystrategy.it/report/renewable-energy-report.html (accessed on 5 August 2019).
- Urbanucci, L.; Bruno, J.C.; Testi, D. Thermodynamic and economic analysis of the integration of high-temperature heat pumps in trigeneration systems. Appl. Energy 2019, 238, 516–533. [Google Scholar] [CrossRef]
- Eurostat, European Commission. Energy Statistics–Prices of Natural Gas and Electricity. Available online: https://ec.europa.eu/eurostat/web/energy/data/database (accessed on 5 August 2019).
- Energy efficiency report 2018, Politecnico di Milano. Available online: http://www.energystrategy.it/assets/files/EER_18_web.pdf (accessed on 5 August 2019).
- Commission Decision of 1 March 2013 establishing the guidelines for Member States on calculating renewable energy from heat pumps from different heat pump technologies pursuant to Article 5 of Directive 2009/28/EC of the European Parliament and of the Council. Official Journal of the European Union 2013, 62, 27, Decision 2013/114/EU. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32013D0114&from=EN (accessed on 5 August 2019).






| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|---|---|
| [13] | [37] | [38] | [39] | ||||
| [13] | [23] | [38] | [13] | ||||
| [40] | [23] | [39] | [41] | ||||
| [40] | [23] | [39] | [41] | ||||
| [40] | [23] | [39] | [13] |
| Energy System Configuration | Novel Configuration with Reversible Heat Pump | Traditional Configuration with Boiler and Non-Reversible Electric Chiller |
|---|---|---|
| Internal Combustion Engine (Nominal Electric Power) | 165 kW | 250 kW |
| Absorption Chiller (Cooling Capacity) | 190 kW | 290 kW |
| Reversible Heat Pump (Heating/Cooling Capacity) | 795 kW/660 kW | \ |
| Boiler (Heating Capacity) | \ | 615 kW |
| Electric Chiller (Cooling Capacity) | \ | 575 kW |
| Photovoltaic Panels (Power at STC) | 505 kW | 410 kW |
| Wind Turbine (Nominal Power) | 0 kW | 0 kW |
| Annual Operating Cost | 175.6 k€ | 203.3 k€ |
| Investment Cost | 1199.0 k€ | 1138.0 k€ |
| Equivalent Annual Cost | 288.8 k€ | 310.8 k€ |
| Annual Carbon Dioxide Emissions | 580.7 ton | 694.9 ton |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urbanucci, L.; Testi, D.; Bruno, J.C. Integration of Reversible Heat Pumps in Trigeneration Systems for Low-Temperature Renewable District Heating and Cooling Microgrids. Appl. Sci. 2019, 9, 3194. https://doi.org/10.3390/app9153194
Urbanucci L, Testi D, Bruno JC. Integration of Reversible Heat Pumps in Trigeneration Systems for Low-Temperature Renewable District Heating and Cooling Microgrids. Applied Sciences. 2019; 9(15):3194. https://doi.org/10.3390/app9153194
Chicago/Turabian StyleUrbanucci, Luca, Daniele Testi, and Joan Carles Bruno. 2019. "Integration of Reversible Heat Pumps in Trigeneration Systems for Low-Temperature Renewable District Heating and Cooling Microgrids" Applied Sciences 9, no. 15: 3194. https://doi.org/10.3390/app9153194
APA StyleUrbanucci, L., Testi, D., & Bruno, J. C. (2019). Integration of Reversible Heat Pumps in Trigeneration Systems for Low-Temperature Renewable District Heating and Cooling Microgrids. Applied Sciences, 9(15), 3194. https://doi.org/10.3390/app9153194






