Online Knowledge Learning Model Based on Gravitational Field Theory

Abstract

Currently, low-dimensional embedded representation learning models are the mainstream approach in knowledge representation research, due to ease of calculation and ability to utilize the spatial relationship between knowledge areas, which benefit from static knowledge learning. However, these models cannot update and learn knowledge online. Although using update strategies to update the knowledge base has been proposed by some scholars, this still requires retraining of knowledge and does not use the previous learning parameters and models. TransOnLine, an online knowledge learning method based on the theory of gravitational field, inspired by the fact that the forces acting on two objects in a gravitational field are only related to the distances between objects, rebalances the knowledge space caused by new knowledge through dynamic programming via introducing the spatial energy function and energy transfer function to solve the above problems. TransOnLine can reuse the parameters and models of previous learning. Experiments show that the performance of the TransOnLine method is close to state-of-the-art methods, and it is suitable for online learning and updating a relational-intensive knowledge base.

1. Introduction

Knowledge graphs, first named by Google in their Knowledge Graph Project, are widely used in intelligent question answering, search, anomaly detection, and other fields. There are some relatively mature products, such as Knowledge Vault, Wolfram Alpha, Data.gov, and so on [1]. Commercial antifraud and precision marketing are more successful application scenarios [2]. Among various knowledge representation learning methods, encoding knowledge into low-dimensional vectors and continuous space, which have been proven to be easy to compute and helpful for knowledge representation [3,4,5], have shown state-of-the-art performance [6].

In recent years, many scholars have proposed different methods for knowledge embedded representation learning, such as Structured Embeddings(SE) [7], Latent Factor Model(LFM) [8], Translating Embeddings(TransE) [9], TransA [10], Description-Embodied Knowledge Representation Learning(DKRL) [11], TransC [12], and others. All of these models, according to the operator in loss function, can be divided mainly into several categories [13,14]: translation-based models, multiplicative models, and deep learning models.

The translation-based models inspired by word2vec are easy to train and effective with good performances. These are usually given “triple” (head, relation, tail), often named h, r, and t; TransE learns the vectors for h, r, and t by h+r≈t, which indicates that the vector t is obtained by translating vector r from vector h. Its loss function is $los{s}_r\left(h,t\right)=\parallel h+r-t{\parallel }_{L1/L2}$. TransE is good with 1-to-1 relations, but when handling complex relations, such as N-to-N, 1-to-N, and N-to-1 relations, TransE shows poor performance because of its simple loss function [3]. TransH [15] uses projection of the entity to the plane of the corresponding relation to adapt complex relation problems in TransE. The vector of entities is projected to the hyperplane of relation $r$ to get $h_r=h-w_r^{T}h{w}_r$ and $t_r=t-w_r^{T}t{w}_r$. TransR and CTransR [16] set a transfer matrix $M_r$ to make the sub-vector space, to which the method maps the embedded entity for each relation $r$, as different relations should have different semantic spaces. In TransA [10], the distance measure of the loss function is changed to Mahalanobis distance, which was proposed in order to learn the different weights for each dimension of the entities and relations. Its loss function is $los{s}_r\left(h,t\right)={\left(h+r-t\right)}^T{W}_r\left(h+r-t\right)$. TansAH [17] employs Mahalanobis distances in TransH and sets the weight matrix $W_r$ to the diagonal matrix, and has achieved good results. TransD considers the transfer matrix $M_r$ in TransR as $M_{rh}$ and $M_{rt}$, which are related to both entities and relations. TranSparse [18] uses sparse matrices instead of dense matrices in TransR, while TransG [19] considers that the different semantics of relation $r$ obey multiple Gaussian distributions. KG2E [20] uses Gaussian distribution to represent entities and relationships.

Multiplicative models define product-based functions over embedded vectors. In LFM, the second order relationship between entities and relations is depicted by relation-based bilinear transformation, which defines the score function of every existing triple (h, r, t) as $scor{e}_r\left(h,t\right)=l_h^T{M}_r{l}_t$, where l is the embedding vector for head or tail, $M_r\in R^{d\ast d}$ is the transformation matrix of the relation $r$, and d is the dimension of the embedding vector. This model is simple but good at cooperative and low-complexity computation. RESCAL [21], which is similar to LFM in relation-based bilinear transformation, has the benefit of optimizing the parameter if the triples do not exist. DISTMULT [22], using the same bilinear function as RESCAL, simplifies the transformation matrix $M_r$ to the diagonal matrix. This simplification gives better performance. Holographic Embeddings(HolE) [23] represents entities and relations as vectors $l_h$, $l_t$, and $l_r$ in $R^d$ and performs cycle-related operations between both entities as ${\left[l_h\ast l_t\right]}_k={\displaystyle \sum }_{i=0}^{d-1}{l}_{h_i}\ast l_{t_{\left(i+k\right)\%d}}$. HolE keeps the simplicity of DISTMULT and expressive power of RESCAL. To model asymmetric relations, Complex Embeddings(ComplEx) [24] introduces complex-valued embedding among DISTMULT. SimplE [13] improves the expressive ability and performance by simplifying the tensor decomposition model and considering the inverse relation. ManifoldE [25] introduces manifold to solve the problem of a multi-solution of an ill-posed algebraic system in knowledge representation learning to improve the accuracy of link prediction. TuckER [26] is a relatively simple but powerful model based on Tucker decomposition of the binary tensor representation of knowledge graph triples.

Deep learning models often use deep neural networks and other information in knowledge bases to get a better performance. It is significant using more information in knowledge bases, such as textual information. DKRL directly learns vector embedding from entity descriptions, which is useful in knowledge graph completion by using a brief description to represent a new entity. TransC learns embedding for instances, concepts, and relations in the same space by using concepts and instance information in the knowledge base. Path-based TransE(PTransE) [27] considers path-based representation for the vector of the relation path. The mirror of inverse relation and an encoding–decoding model consisting of Recurrent Neural Networks are introduced in Semantical Symbol Mapping Embedding(SSME) [14] to improve the ability of knowledge expression. ConvE [28] applies 2D convolution directly in the embedding process, thus inducing spatial structure in the embedding space.

When using the above methods for training, these methods first need to extract all entities and relationships in the knowledge base, then learn the triples in the knowledge base. The above methods tend to learn static and outdated triples, and cannot update models when new or modified triples that only include existing entities and relationships are added to the knowledge base. Although some algorithms propose using strategies to update the knowledge base, they are still retrained without using the results of previous training [29], such as Liang [30] proposed to construct a update frequency predictor based on hot entities, update the knowledge from the Internet to the knowledge base, then retrain and learn the knowledge base. Obviously, this method only reduces the frequency of retraining the whole knowledge base when the knowledge changes, but cannot be learned and updated online. For example, in the knowledge graph of elderly diseases, the diseases of the elderly may change over time. Once the disease information of the elderly changes, current methods need to retrain all entities and relationships in this knowledge base to obtain the latest knowledge representation model. We need a learning method that only updates the knowledge related to this individual; other knowledge need not be updated. This method should adapt to the growth of knowledge without retraining.

To learn changed knowledge online without retraining the whole knowledge base and only updating the change-related knowledge, we propose a novel translation embedding method named TransOnLine. In our method, we assumed that changed knowledge will have some impact and the impact will spread in the knowledge space, inspired by the theory of gravitational field, which describes the spatial effects of gravitation and its propagation in space. Our work can be summarized as follows: (1) We understand current knowledge representation methods of the perspective of dynamic programming and explain why current methods do not learn and update online; (2) we refer to the theory of gravitational field to define some functions we call energy functions and path-based energy propagation. Experiments on data FB15K and WN18 [31] show that the method can learn and update knowledge online and the performance in entity prediction of TransOnLine is not much different to current advanced methods.

2. Materials and Methods

2.1. Understanding Knowledge Representation Learning

As we know, knowledge representation learning needs to convert the high-dimensional discrete space to low-dimensional continuous space, and the new space can characterize most of the nature of the original space regarding graphs of knowledge. TransE is a more convincing method, which can better preserve the adjacency of entities in 1-to-1 relations, but does not conserve the complex relations.

Moreover, all of the current methods can be considered as the resolvent of the problem of space transformation by dynamic programming (DP). For example, we can understand TransE by DP as that it defines objective space as $R^d$ and the entity is described as vector $V_{e_i}=\left(x_1^i,x_2^i,\dots ,x_d^i\right),$ and the relation is $V_{r_j}=\left(x_1^j,x_2^j,\dots ,x_d^j\right)$, i = 1,2,…n, j = 1,2,…m, while $n$ is the number of entities and $m$ is the number of relations. TransE is a method for looking at every entity and every relation’s parameter $x_n^i$. The total number of parameters of entities and relations is $\left(n+m\right)d$, which is too large to train when the dataset is huge, so we change the parameter of the triple (h, r, t) using the equation of state transition: $v_{e_h}=v_{e_h}+\mathsf{\lambda }\nabla \left[distance\left(v_{e_h}+v_r,v_{e_t}\right)-distance\left(v_{e_{h^{\prime }}}+v_r,v_{e_{t^{\prime }}}\right)\right]$. To reinforce computational performance, we use negative sampling for $v_{e_h}$ to $v_{e_{h^{\prime }}}$, $v_{e_t}$ to $v_{e_{t^{\prime }}}$, but only one sampling for h and t. The objective function is $\underset{x}{\mathrm{argmin}}distance\left(v_{e_h}+v_r,v_{e_t}\right)-distance\left(v_{e_{h^{\prime }}}+v_r,v_{e_{t^{\prime }}}\right)$. When training the dataset, the same x will change many times, and the optimal x will be obtained in the global scope.

When knowledge is changed in the knowledge base, it needs at least 1 epoch to train all of the knowledge by TransE, and each parameter x will be calculated at least once to obtain the optimal result of the objective function. This makes the computation very large. The number of x parameters that need to be updated will be $\left(n+m\right)d$. The method will calculate at least the number of triples in the knowledge base. These calculations are difficult to complete in less time. Therefore, we need to reduce the number of updates to x parameters in the TransE epoch, that is, to reduce the number of entities and relationships involved in the updates.

2.2. Gravitational Field Theory

Our approach focuses on how to reduce the scale of variation parameters while knowledge is changed. Inspired by the theory of gravitational field in general relativity, it is said that the force of two certain objects is only related to the distance between them. The Einstein field equation is $G_{uv}=R_{uv}-\frac{1}{2}{g}_{uv}R=\frac{8\pi G}{c^4}{T}_{uv}$, where $G_{uv}$ is called the Einstein tensor, $R_{uv}$ is the curvature term to represent spatial curvature, $R$ is the scalar of curvature, $g_{uv}$ is a four-degrees-of-freedom metric tensor, $T_{uv}$ is the stress–energy tensor, c is the speed of light in the vacuum, and $G$ is Newton’s gravitational constant [32]. When space–time is uniform and used in both the weak-field approximation and the slow-motion approximation, The Einstein field equations are reduced to Newton’s law of gravity [33] as $F=\frac{GMm}{r^2}$, where $r$ is the distance between two objects. It is said that for a given body, the gravitation is proportional to the square of the distance. If the space–time is not uniform or not weak-field, $G$ will be changed, and the space–time will expand or contract [34].

2.3. Online Knowledge Learning Method

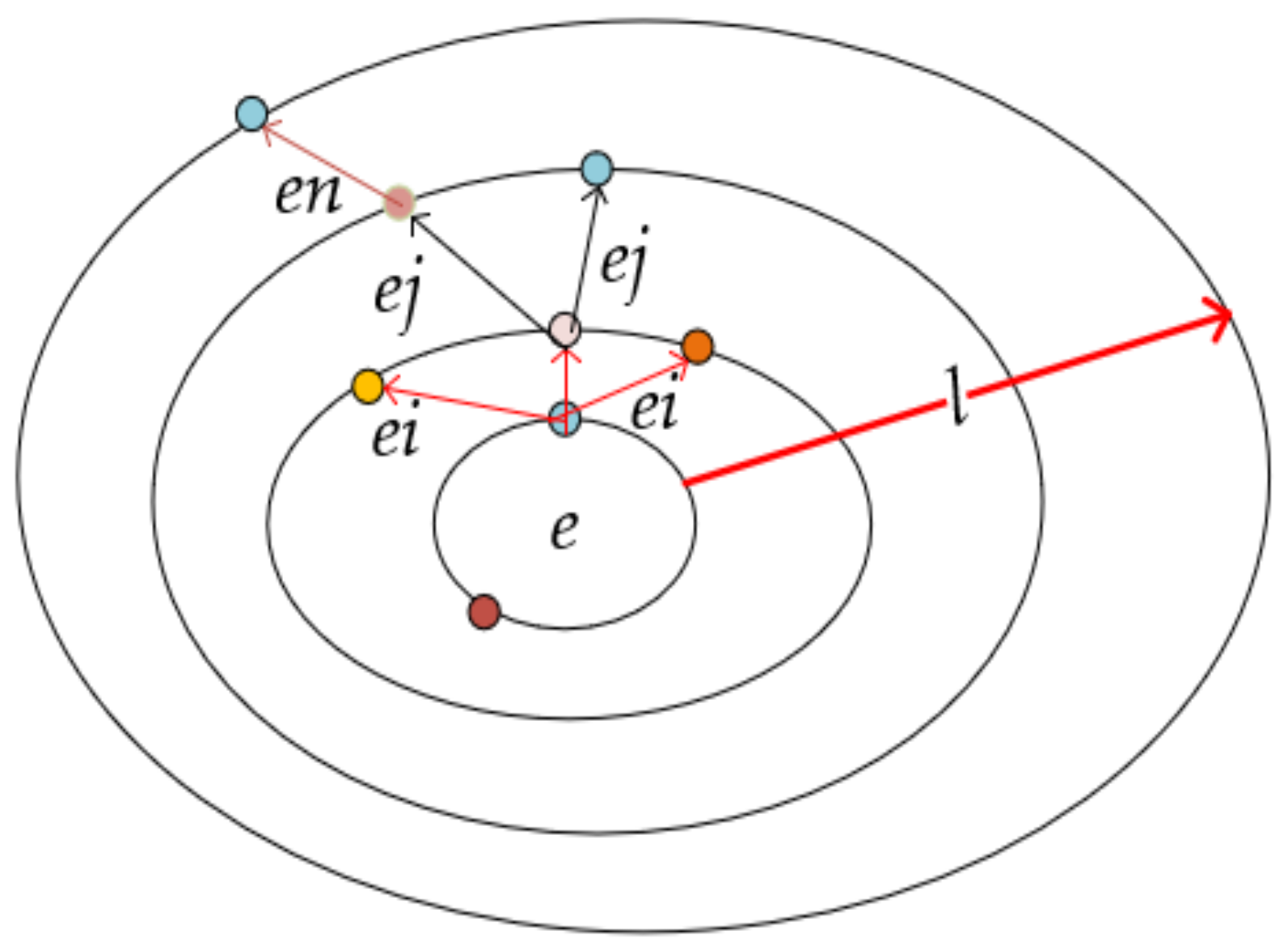
When training the knowledge bases using different methods, often setting the embedding dimension—one of the super parameters—indicates that the scope of the knowledge space will not be changed and the space of the embedding dimension will not expand or contract. Therefore, we assume that the knowledge space s is uniform, the same as the Gravitational field, and the influence of a certain knowledge space on another knowledge space is only related to the distance between the two knowledge spaces. When one area of knowledge in the space has been changed, referencing gravitational field theory, the energy e and the impact that knowledge change made need to be distributed among relative knowledge, which are accessed from the changed knowledge and will be absorbed within a limited range. Reachable step l is used in the knowledge base to identify the distance between knowledge spaces. Different hyperplanes can be formed by taking the changed knowledge entities as the center. The absorption of e by the entities in each isopotential hyperplane is the same, which is only related to the step l, representing construction of the isopotential surface.

The knowledge base $\mathrm{KB}=\left(E,R,F, U\right)$, where E is the entity list, R is the relation list, F is the old fact triple list, U is the new fact triple list, one of which is also called an event; when an event in U has happened, it will change into a fact triple and add this triple into F. In this hypothesis, for some fact triples, such as (e1, r1, e2), (e1, r2, e3), (e2, r3, e4), if e1 in the space $s$ is changed, the influence of e2 will be the same as e3’s and will be bigger than e4’s. This is because the distance between e1 and e2 and between e1 and e3 is all one unit, while the distance between e1 and e4 is two units. The issue of how this impact can be distributed into e1, e2, e3, e4, r1, r2, r3 while still keeping the spaces original nature of $s$ is a DP problem. In this problem, we need to define the energy function of different knowledge changes and find an energy propagation function to distribute the impact for relative knowledge, corresponding to the state and state transition functions in DP.

For an event (h, r, t), the energy e generated as Formula (1) is directly proportional to the number of entities or relationships involved in the event, and is inversely proportional to the frequency of the event. The variable DUO represents the number of relationships that connect entities h or t, while function frequency is used to express the sum of any number of occurrences of h, r, or t in current F. When traversing an event in F set, a directed tree of entities and relationships will be formed, where l represents the shortest step mentioned above between any node and other node, where k is a constant of the energy coefficient, and DELTA is the square error that can use $v_{e_h}{}^2+v_r{}^2-v_{e_t}{}^2$ to compute; $frequency\left(x\right)$ is the number of entity x in the history of the event, for example, the history of the event is ((e1, r1, e2), (e1, r2, e3), (e2, r2, e4)), and $frequency\left(e1\right)=2$, $frequency\left(e2\right)=2$,$frequency\left(r1\right)=1$, $frequency\left(e3\right)=1$, and so on.

$$\mathrm{E}=\frac{k\ast DUO\ast DELTA}{frequency\left(h\right)+frequency\left(t\right)+frequency\left(r\right)}.$$

(1)

In gravitational field theory, the same force is obtained with the same distance from two particles to an object. Our energy propagation function displays the same influence for entities with the same distance to the event triple. The energy propagation function is shown as Equation (2):

$$E_{e_i}=E\ast \frac{ei\_total\_entities}{all\_total\_entities}\ast \frac{1}{ei\_brother\_entities}\ast Su{b}_{ei}$$

(2)

where $E_{e_i}$ is the dissipated energy of entity ei, which is obtained from an event, $all\_total\_entities$ is the number of all entities accessed from the entity in the event triple through step $l$, which does not include the entities in this event triple, $ei\_total\_entities$ is the number of entities where the node $e_i$ can arrive at step $l-l_o$, $l_o$ is the step from the nearest entity in event triple to ei, $ei\_brother\_entities$ is the number of brother entities listed for ei, with the list including ei, $Su{b}_{ei}=1$ where $e_i$ does not have a child and $Su{b}_{ei}=0.5$ if $e_i$ has one or more children. $E_{e_i}$ is absorbed by the node $e_i$, equal to the total energy of $e_i$’s children. The update function is $v_{e_i}=v_{e_i}+E_{e_i}$, the loss function is $total\_loss={\left|v_h+v_r-v_t\right|}_{L1/L2}+{\displaystyle \sum }_{\left(h^{\prime },r^{\prime },t^{\prime }\right)\in travel\_triples}{\left|v_{h^{\prime }}+E_{h^{\prime }}+v_{r^{\prime }}-\left(v_{t^{\prime }}+E_{t^{\prime }}\right)\right|}_{L1/L2}$, where $travel\_triples$ are triples of the path in the tree g by the step of $l$ from the changed knowledge. As shown in Figure 1, the isopotential hyperplane in the knowledge space is represented by an ellipse, while dots on ellipses represent knowledge entities in space. Knowledge dots that are on the same isopotential hyperplane and are from the same knowledge dot on the inner isopotential hyperplane are brother entities. The entities between adjacent equipotential hyperplanes pass through the relationship to form the parent–child relationship, which is represented by arrows. The energy e, generated by changed knowledge, propagates in a certain range l and is absorbed by entities. The energy can propagate equally to entities from an isopotential hyperplane to an adjacent equipotential hyperplane, but these energies can be absorbed by entities on the same isopotential hyperplane and by their child entities.

The TransOnLine method, as shown in Appendix A, after initializing embedding vectors Ve and Vr, learns the vector from set F with TransE, and then trains the set U by using energy function and energy propagation function. Compared with traditional knowledge learning methods, TransOnLine can reduce the training parameters used to update knowledge. The number of parameters that need to be updated is (all_total_entities+all_total_relations)*d, which is far less than the number of retraining parameters. Through updating local parameters, online knowledge learning can be realized.

2.4. Experiment Setting

To verify TransOnLine, our experiments on the task of link prediction were conducted on two public datasets FB15K and WN18, which are the subsets of WordNet and Freebase and were used in previous work [31]. The statistics of datasets in our experiments are shown as

Table 1. The statistics of number of triples in our experiment.

Dataset	#Relation	#Entity	#Train	#Valid	#Test
FB15K	1345	14,951	483,142	50,000	59,071
WN18	18	40,943	141,442	5000	5000

.

The same evaluation measure is used as in previous leaning methods. To measure prediction of a missed head entity (or tail entity), we used MeanRank, also called MR and Hit@10. Firstly, we replace tail t (or head h) for every test triple (h, r, t) that is not filtered, then we order the prediction result by descending probabilistic score. The MeanRank is the average of the rank index number of the missed entity in the ordered result. Hit@10 is the average of a rank index number that is not great than 10. A higher hit@10 and lower MeanRank indicate better performance. To better observe the performance differences between TransOnLine and TransE, we note that the MeanRank in TransE test is a1, the MeanRank in TransOnLine test is a2, the Hit@10 in TransE test is h1, and the Hit@10 in TransOnLine test is h2. Let F1 = a1/a2, F2 = h2/h1, so the bigger F1 and F2 are, the better effect of TransOnLine. Referring to Openke [35], the parameters of TransD, TransH, and TransR methods are set.

We implement TransOnLine, TransE, and other methods with Tensorflow [36] by ourselves. As in previous research [15], we directly set TransE’s parameter learning rate as α = 0.001, margin γ = 0.25, embedding dimension k = 100, batch size B = 60, epoch = 1000, as in previous work. TransOnLine’s parameters are the same as TransE’s, and set step l = 1. For WN18, we set α = 0.01, γ = 1, k = 128, B = 75, epoch = 1000, with the same configuration for TransOnLine, where step l = [1,2,3]. We use C = F/(F + U) to represent the proportion of old fact triples F to training sets, and C is among (0.95,0.98,0.99).

3. Results and Discussion

3.1. Validation of Online Learning Effectiveness

Let step l = 1, and let C take different values to verify the effectiveness of TransOnLine online learning. Figure 2a shows the results of head entity prediction, where the header entity h in test triple (h, r, t) is replaced. In Figure 2a, the F1 and F2 increase with the increase of C on FB15K, which shows that in FB15K, the larger the F set, the fewer samples to be learned online, and the better the performance of TransOnLine relative to TransE. Figure 2b shows the results of tail entity prediction when the tail entity t in the test triple (h, r, t) is replaced. In Figure 2b, F1 and F2 decrease with the increase of C on WN18, which shows that in the WN18 set, the smaller the F set, the greater the amount of online learning, and the better the effect of TransOnLine relative to TransE.

In order to verify whether the above results are contingent or not, and to exclude the influence of data sequence on the experimental results, we merge the training set, test set, and validation set of the original dataset, then randomly generate a new training set, test set, and validation set, as in Table 1. The results of many experiments on new datasets that are randomly generated are consistent with those above. In order to explain this phenomenon, the corresponding datasets are studied. We found that the average number of connections per entity in FB15K and WN18 is 39.6 and 3.6 when step l = 1. Compared with WN18, the relationship between entities in FB15K is more complex, which indicates that TransOnLine can achieve better results for a small number of samples in online training of a dense relationship knowledge base.

3.2. Verification of Spatial Distance Correlation

In order to verify TransOnline’s hypothesis in knowledge space that the energy generated by events propagates among adjacent knowledge, experiments were carried out on WN18 to make C = 0.99 and l = (1,2,3). The experimental results are shown in Figure 2c. In head entity prediction or tail entity prediction, F1 increases with the increase of l, while F2 is an inflection point at l = 2, as shown in Figure 2c. To explain this phenomenon, Dimension Reduction Analysis, DRA [37], was used in the vectors learned when l=2 and l=3. Random selection of 30000 entities, using PCA algorithm to reduce the entity vector to two dimensions, the results are shown in Figure 3. It is found that the spatial distribution of entity vectors learned with l = 3 is more uniform than with l = 2 (shown in Figure 3), so if smaller MR is obtained for the same entity prediction, more entities can be predicted, and Hit@10 is relatively smaller. Therefore, spatial distance has an impact on TransOnline performance. It is necessary to choose a reasonable spatial distance to obtain better values for MR and Hit@10.

3.3. Compare with Static Learning Method

At the same time, we select TransOnLine’s best results on FB15K and WN18 datasets for comparison with other methods. In

Table 2. The result of performance on these methods.

	FB15K		WN18
	MeanRank	Hit@10	MeanRank	Hit@10
TransE	316	0.40	425	0.41
TransR	263	0.43	381	0.43
TransH	302	0.48	447	0.40
TransD	219	0.57	346	0.54
TransOnLine	225	0.55	354	0.49

, MaenRank and Hit@10 are the average values of the sum of the results of the corresponding prediction for head and tail entities. Table 2 shows that TransOnLine performs better than TransH, TransR, and TransE in FB15K and WN18 datasets, but performs worse than TransD. The main reason is that TransOnLine has the characteristics of a simple relationship in TransE learning and is not able to learn knowledge for complex relationships.

4. Conclusions

In this paper, we introduce TransOnline, a new method that can learn knowledge online based on the theory of gravitational field and rebalance knowledge spaces with the idea of dynamic programming by constructing the spatial energy function and energy transfer function. In this way, the knowledge base can be updated and learned online. Experiments show that TransOnLine can learn knowledge bases with intensive relationships very well, and its performance is close to the current mainstream learning methods. The next step is to further optimize the proposed TransOnLine method in order to achieve better performance, especially in dealing with complex relationship types. This may lead to performance improvement when using DP on the basis of TransD space and may rebalance the energy generated by knowledge change. It may also increase the learning ability for complex knowledge by improving the energy function and the energy transmission function.