An Improved Second-Order Blind Identification (SOBI) Signal De-Noising Method for Dynamic Deflection Measurements of Bridges Using Ground-Based Synthetic Aperture Radar (GBSAR)
Abstract
:1. Introduction
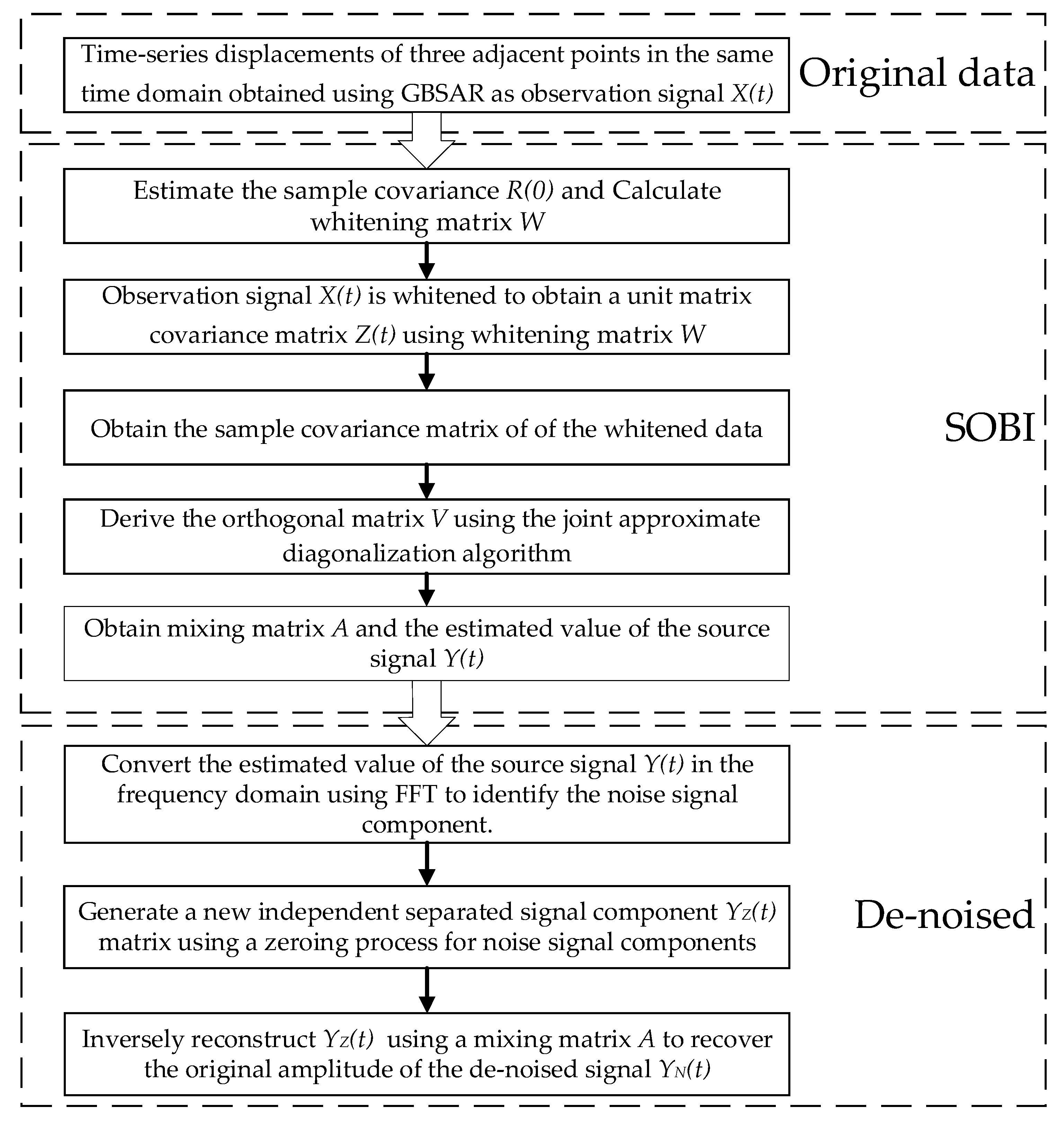
2. Methodology
2.1. BSS Model
- (1)
- Mixing matrix, A, is a column full-rank matrix.
- (2)
- The source signals are the zero-mean random signals that are not correlated in the time-space domain and correlated in the time domain.
- (3)
- The source signal and noise are independent.
- (4)
- The number of source signals is less than or equal to the number of the original signals.
2.2. Improved SOBI
2.3. Accuracy Assessment
3. Simulated Experiment and Analysis
4. On-Site Experiment and Analysis
4.1. Site Description and Data Acquisition
4.2. Results Analysis and Discussion
5. Conclusions
- (1)
- A simulation experiment was performed to validate the feasibility of the improved SOBI signal de-noising method where three mixed signals were linearly mixed using three sets of simulation source signals with different frequency scales. The obtained correlation coefficients between each simulated source signal and the corresponding separated signal component were all greater than 0.99. The results showed that the improved SOBI signal de-noising method effectively distinguished the useful signals and noise signals from the mixed signals, which can be useful for signal de-noising of time-series displacements obtained using GBSAR.
- (2)
- By fully considering the characteristics of the high-distance resolution GBSAR technique, the obtained dynamic time-series displacements of three adjacent monitoring points in the same time domain were selected as input signals. This was done in order to obtain the de-noised time-series displacement of the middle point among three adjacent monitoring points by using the improved SOBI signal de-noising method. Using a spectrum analysis, the separated noise components were effectively determined from the separated signals, and the original amplitude of the de-noised signal was recovered using an inverse reconstruction with a mixing matrix. The results showed that the improved SOBI signal de-noising method not only reduced the noise caused by the surrounding environment, but also reduced the noise caused by vibrations of the monitoring instrument.
- (3)
- Compared with the EDM and EEMD signal de-noising methods, the improved SOBI signal de-noising method displayed a greater improvement in the indexes of NRR, NM, and SER for the obtained time-series displacement of a bridge using GBSAR. The results indicate that the improved SOBI signal de-noising method has a powerful signal de-noising ability.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Riveiro, B.; González-Jorge, H.; Varela, M.; Jauregui, D.V. Validation of terrestrial laser scanning and photogrammetry techniques for the measurement of vertical underclearance and beam geometry in structural inspection of bridges. Measurement 2013, 46, 784–794. [Google Scholar] [CrossRef]
- Liu, X.; Wang, P.; Lu, Z.; Gao, K.; Wang, H.; Jiao, C.; Zhang, X. Damage detection and analysis of urban bridges using terrestrial laser scanning (TLS), ground-based microwave interferometry, and permanent scatterer interferometry synthetic aperture radar (PS-InSAR). Remote Sens. 2019, 11, 580. [Google Scholar] [CrossRef]
- Monserrat, O.; Crosetto, M.; Luzi, G. A review of ground-based SAR interferometry for deformation measurement. ISPRS J. Photogramm. 2014, 93, 40–48. [Google Scholar] [CrossRef] [Green Version]
- Rödelsperger, S.; Läufer, G.; Gerstenecker, C. Monitoring of displacements with ground-based microwave interferometry: IBIS-S and IBIS-L. J. Appl. Geodes. 2010, 4, 41–54. [Google Scholar] [CrossRef]
- Farrar, C.R.; Darling, T.W.; Migliori, A.; Baker, W.E. Microwave interferometers for non-contact vibration measurements on large structures. Mech. Syst. Signal Process. 1999, 13, 241–253. [Google Scholar] [CrossRef]
- Granello, G.; Andisheh, K.; Palermo, A.; Waldin, J. Microwave radar interferometry as a cost-efficient method of monitoring the structural health of bridges in New Zealand. Struct. Eng. Int. 2018, 28, 518–525. [Google Scholar] [CrossRef]
- Stabile, T.A.; Perrone, A.; Gallipoli, M.R.; Ditommaso, R.; Ponzo, F.C. Dynamic survey of the musmeci bridge by joint application of ground-based microwave radar interferometry and ambient noise standard spectral ratio techniques. IEEE Geosci. Remote Sens. Lett. 2013, 10, 870–874. [Google Scholar] [CrossRef]
- Pieraccini, M.; Parrini, F.; Fratini, M.; Atzeni, C.; Spinelli, P.; Micheloni, M. Static and dynamic testing of bridges through microwave interferometry. NDT E Int. 2006, 40, 208–214. [Google Scholar] [CrossRef]
- Lim, J.S.; Oppenheim, A.V. Enhancement and bandwidth compression of noisy speech. Proc. IEEE 1979, 67, 1586–1604. [Google Scholar] [CrossRef]
- Malinowski, M.; Kwiecień, J. Study of the effectiveness of different kalman filtering methods and smoothers in object tracking based on simulation tests. Rep. Geod. Geoinformatics 2014, 97, 1–22. [Google Scholar] [CrossRef]
- Guo, X.; Shen, C.; Chen, L. Deep fault recognizer: An integrated model to denoise and extract features for fault diagnosis in rotating machinery. Appl. Sci. 2017, 7, 41. [Google Scholar] [CrossRef]
- Pan, H.X.; Men, J.F. De-noising method research on bearing fault signal based on particle filter. In Proceedings of the Second World Congress on Nature and Biologically Inspired Computing, Fukuoka, Japan, 15–17 December 2010; pp. 311–315. [Google Scholar]
- Ogundipe, O.; Lee, J.K.; Roberts, G.W. Wavelet de-noising of GNSS based bridge health monitoring data. J. Appl. Geodes. 2014, 8, 273–282. [Google Scholar] [CrossRef]
- Su, L.; Zhao, G.L. De-noising of ECG signal using translation—Invariant wavelet de-noising method with improved thresholding. In Proceedings of the IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006; pp. 5946–5949. [Google Scholar]
- Liu, C.; Song, C.; Lu, Q. Random noise de-noising and direct wave eliminating based on SVD method for ground penetrating radar signals. J. Appl. Geophys. 2017, 144, 125–133. [Google Scholar] [CrossRef]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 July 2014; pp. 3842–3849. [Google Scholar]
- Kaleem, M.F.; Guergachi, A.; Krishnan, S.; Cetin, A.E. Using a variation of empirical mode decomposition to remove noise from signals. In Proceedings of the IEEE 21st International Conference on Noise and Fluctuations, Toronto, ON, Canada, 12–16 June 2011; pp. 123–126. [Google Scholar]
- Han, G.; Lin, B.; Xu, Z. Electrocardiogram signal denoising based on empirical mode decomposition technique: An overview. J. Instrum. 2017, 12, P03010. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Gaci, S. A new ensemble empirical mode decomposition (EEMD) denoising method for seismic signals. Energy Procedia. 2016, 97, 84–91. [Google Scholar] [CrossRef]
- Singh, G.; Kaur, G.; Kumar, V. ECG denoising using adaptive selection of IMFs through EMD and EEMD. In Proceedings of the 2014 International Conference on Data Science & Engineering, Kochi, India, 26–28 August 2014; pp. 228–231. [Google Scholar]
- Chen, H.; Chen, P.; Chen, W.; Wu, C.; Li, J.; Wu, J. Wind turbine gearbox fault diagnosis based on improved EEMD and Hilbert square demodulation. Appl. Sci. 2017, 7, 128. [Google Scholar] [CrossRef]
- Cardoso, J.F. Blind signal separation: Statistical principles. Proc. IEEE 1998, 86, 2009–2025. [Google Scholar] [CrossRef]
- Poncelet, F.; Kerschen, G.; Golinval, J.C.; Verhelst, D. Output-only modal analysis using blind source separation techniques. Mech. Syst. Signal. Process. 2007, 21, 2335–2358. [Google Scholar] [CrossRef]
- Belouchrani, A.; Abed-Meraim, K.; Cardoso, J.F.; Moulines, E. A blind source separation technique using second-order statistics. IEEE Trans. Signal Process. 2002, 45, 434–444. [Google Scholar] [CrossRef]
- Wheland, D.; Pantazis, D. Second order blind identification on the cerebral cortex. J. Neurosci. Methods 2014, 223, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Illner, K.; Miettinen, J.; Fuchs, C.; Taskinen, S.; Nordhausen, K.; Oja, H.; Theis, F.J. Model selection using limiting distributions of second-order blind source separation algorithms. Signal Process. 2015, 113, 95–103. [Google Scholar] [CrossRef]
- Gelle, G.; Colas, M.; Serviere, C. Blind source separation: A tool for rotating machine monitoring by vibrations analysis? J. Sound Vib. 2001, 248, 865–885. [Google Scholar] [CrossRef]
- Zhou, W.; Chelidze, D. Blind source separation based vibration mode identification. Mech. Syst. Signal Process. 2007, 21, 3072–3087. [Google Scholar] [CrossRef]
- McNeill, S.I.; Zimmerman, D.C. A framework for blind modal identification using joint approximate diagonalization. Mech. Syst. Signal Process. 2008, 22, 1526–1548. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Seppänen, J.; Turunen, J.; Koivisto, M.; Haarla, L. Measurement based analysis of electromechanical modes with Second Order Blind Identification. Electr. Power Syst. Res. 2015, 121, 67–76. [Google Scholar] [CrossRef]
- Liu, H.T.; Xie, X.B.; Xu, S.P.; Wan, F.; Hu, Y. One-unit second-order blind identification with reference for short transient signals. Inf. Sci. 2013, 227, 90–101. [Google Scholar] [CrossRef]
- Cai, J.H.; Xiao, Y.L.; Li, X.Q. Nuclear magnetic resonance logging signal de-noising based on empirical mode decomposition threshold filtering in frequency domain. Prog. Geophys. 2019, 34, 509–516. [Google Scholar]
- Lv, L.L.; Gong, W.; Song, S.L.; Zhu, B. De-noising process based on wavelet transform in feature reflectance detection LiDAR system. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 56–59. [Google Scholar]
- Lv, L.L. Evaluation system of wavelet de-noising effect for multispectral LiDAR. Hydrogr. Surv. Chart 2016, 36, 72–75. [Google Scholar]
- Liu, X.; Tong, X.; Ding, K.; Zhao, X.; Zhu, L.; Zhang, X. Measurement of long-term periodic and dynamic deflection of the long-span railway bridge using microwave interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4531–4538. [Google Scholar] [CrossRef]










| Signal Components | Correlation Coefficients | ||
|---|---|---|---|
| 0.9933 | −0.0173 | 0.0555 | |
| 0.1155 | 0.9999 | −0.0133 | |
| −0.0016 | 0.0003 | 0.9984 | |
| Index | EMD | EEMD | SOBI |
|---|---|---|---|
| NRR (db) | −2.3393 | 3.2862 | 6.7116 |
| NM (mm) | 2.5066 | 0.7211 | 3.7622 |
| SER | 0.9870 | 0.9947 | 1.0012 |
| RMSE (mm) | 0.0264 | 0.0073 | 0.0120 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, H.; Huang, M.; Yang, W. An Improved Second-Order Blind Identification (SOBI) Signal De-Noising Method for Dynamic Deflection Measurements of Bridges Using Ground-Based Synthetic Aperture Radar (GBSAR). Appl. Sci. 2019, 9, 3561. https://doi.org/10.3390/app9173561
Liu X, Wang H, Huang M, Yang W. An Improved Second-Order Blind Identification (SOBI) Signal De-Noising Method for Dynamic Deflection Measurements of Bridges Using Ground-Based Synthetic Aperture Radar (GBSAR). Applied Sciences. 2019; 9(17):3561. https://doi.org/10.3390/app9173561
Chicago/Turabian StyleLiu, Xianglei, Hui Wang, Ming Huang, and Wanxin Yang. 2019. "An Improved Second-Order Blind Identification (SOBI) Signal De-Noising Method for Dynamic Deflection Measurements of Bridges Using Ground-Based Synthetic Aperture Radar (GBSAR)" Applied Sciences 9, no. 17: 3561. https://doi.org/10.3390/app9173561
APA StyleLiu, X., Wang, H., Huang, M., & Yang, W. (2019). An Improved Second-Order Blind Identification (SOBI) Signal De-Noising Method for Dynamic Deflection Measurements of Bridges Using Ground-Based Synthetic Aperture Radar (GBSAR). Applied Sciences, 9(17), 3561. https://doi.org/10.3390/app9173561






