Simultaneous Verification of Multi-Ultrasonic-Flowmeters in Tandem Arrangement for Natural Gas
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
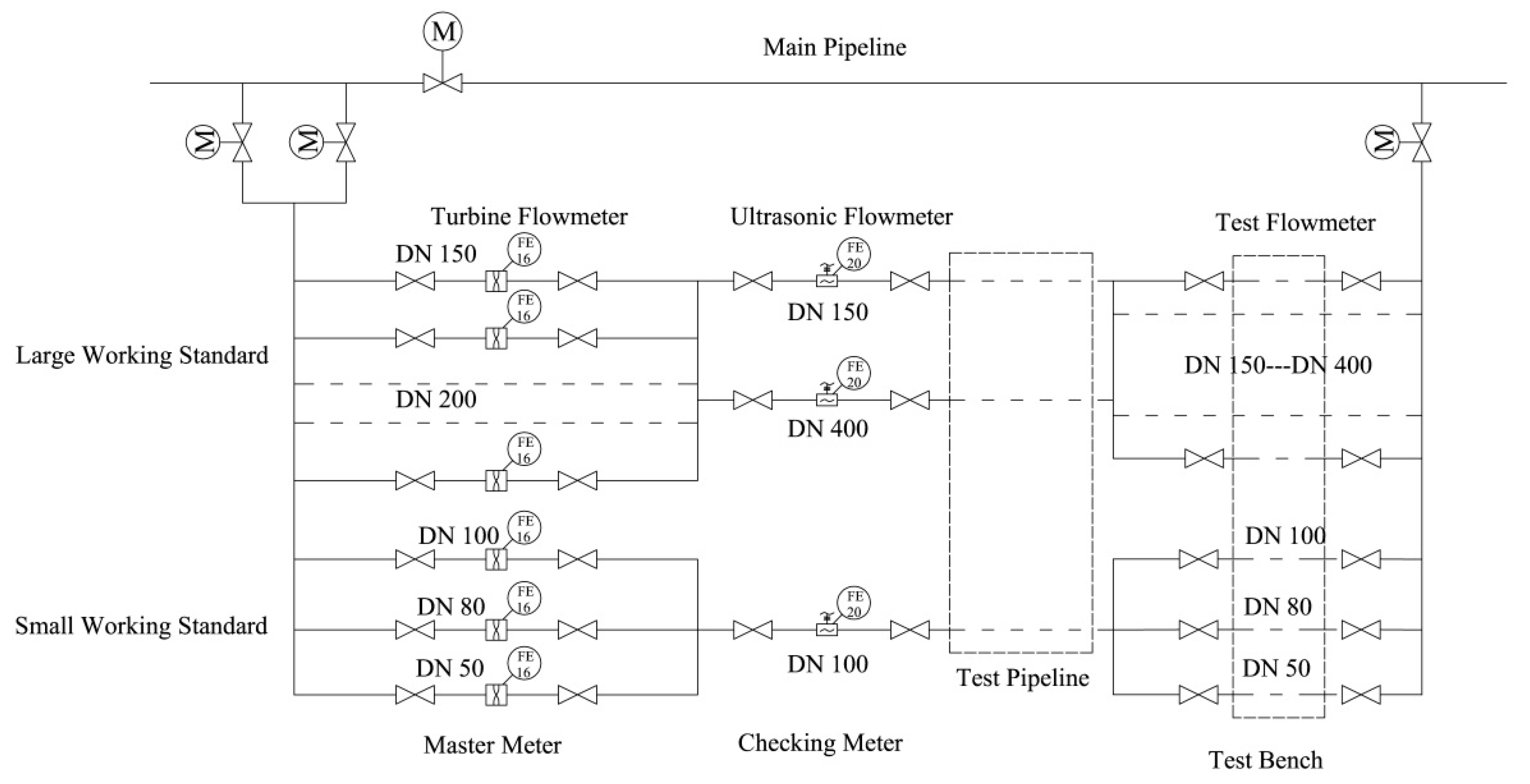
2.1. Experimental Method
2.2. Numerical Methods
3. Results
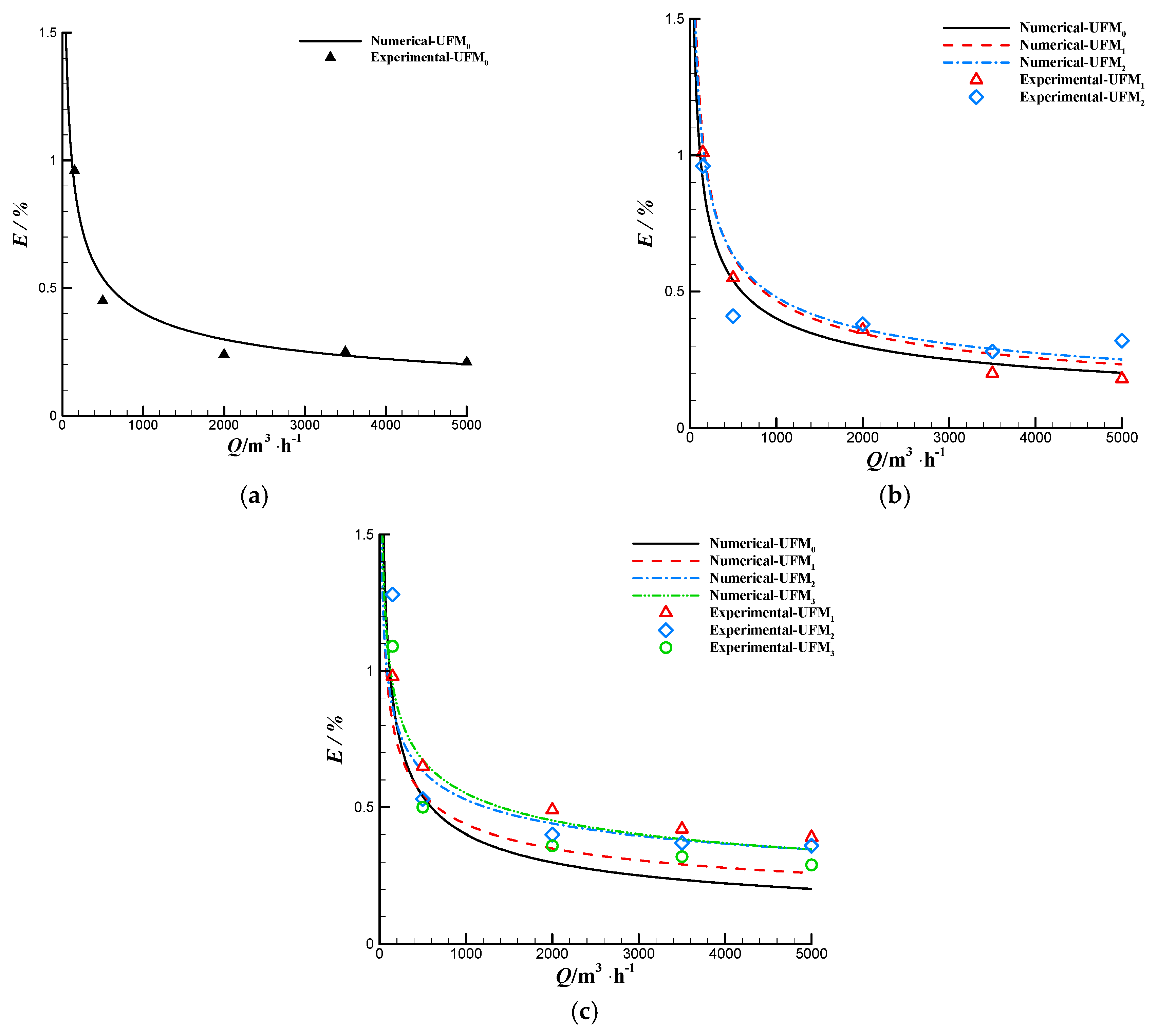
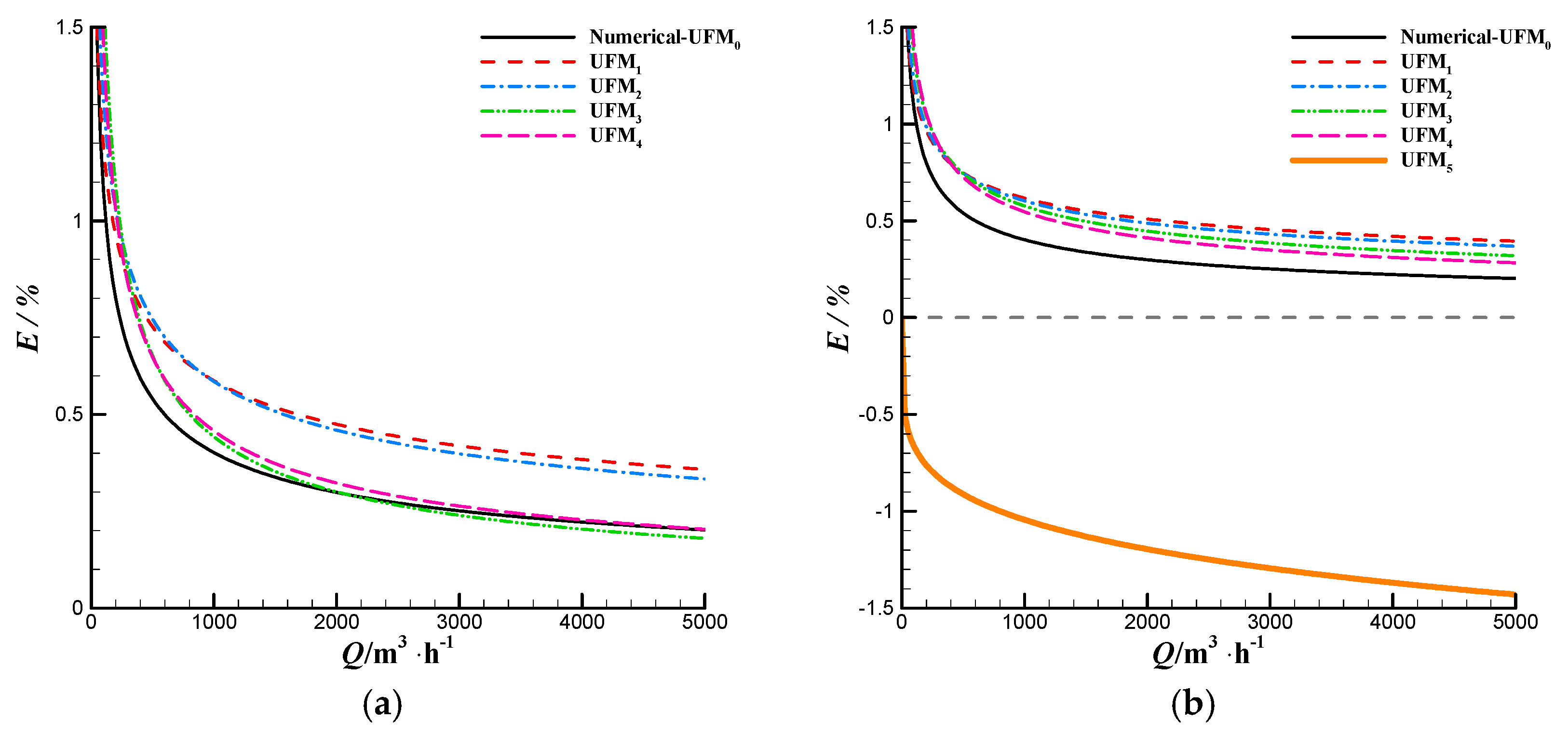
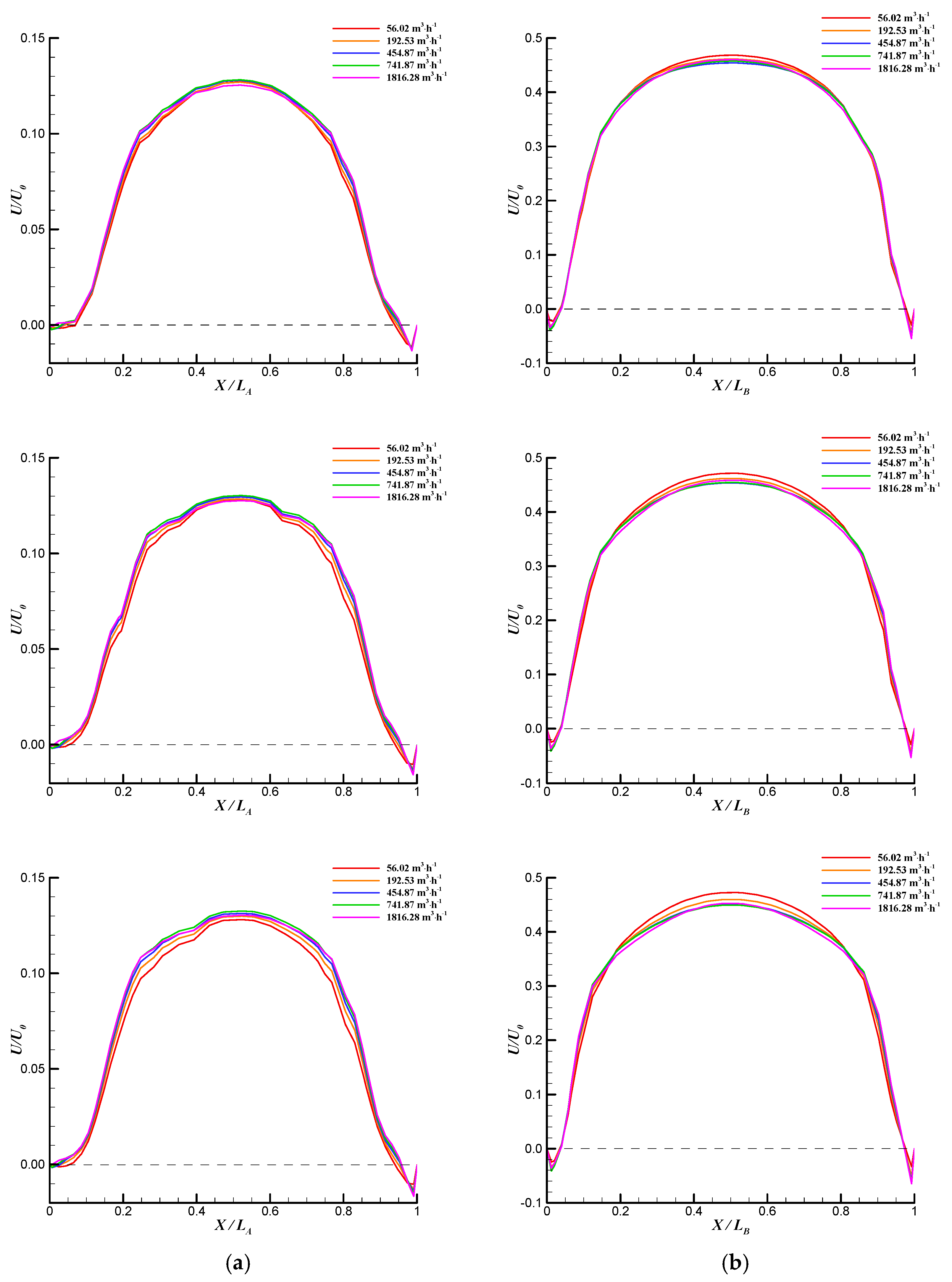
3.1. Numerical Simulation Verification by Experiments for 1–3 Tested DN 250 UFMs
3.2. Numerical Simulation Verification by Experiments for 4–5 Tested DN 250 UFMs
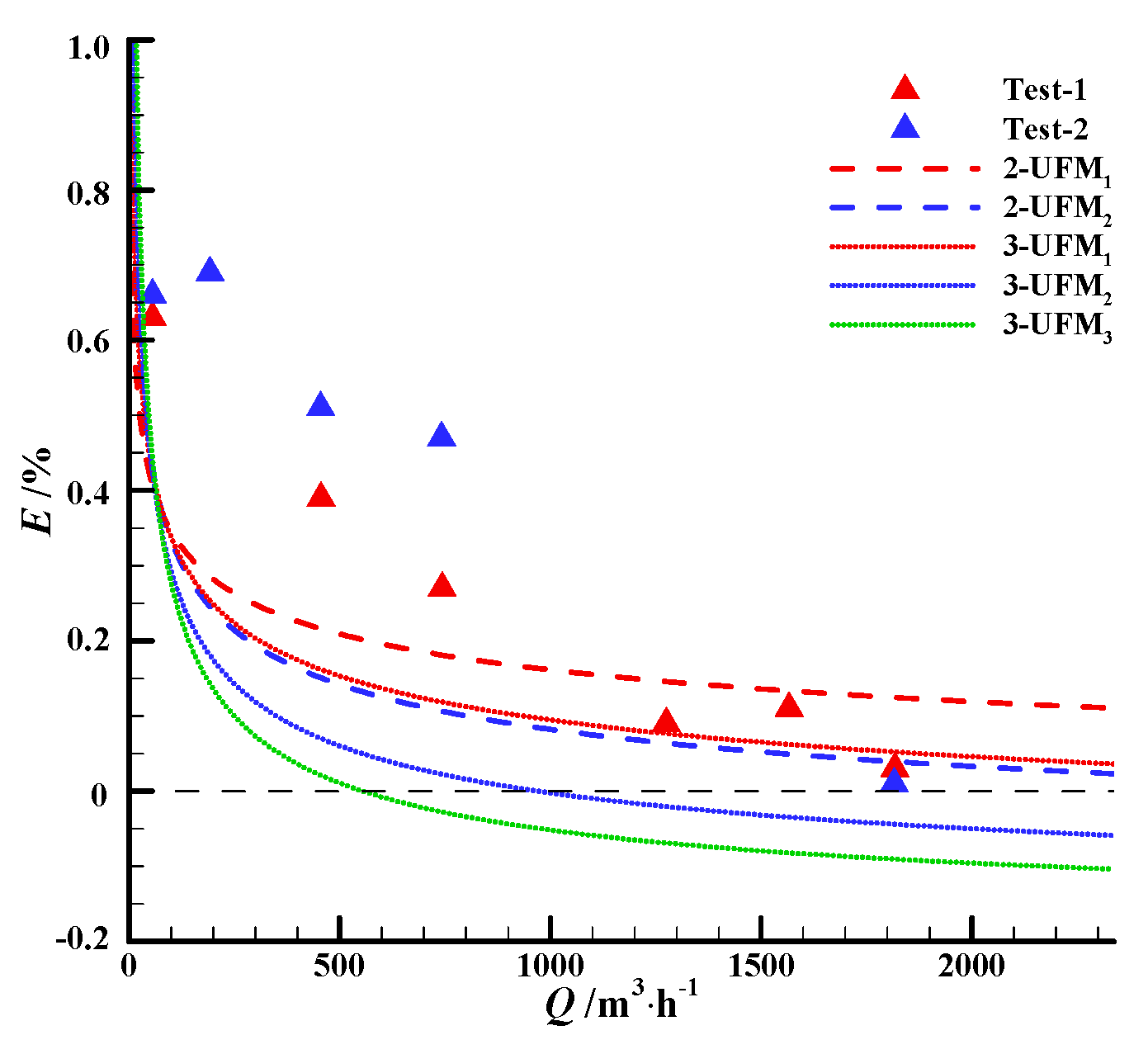
3.3. Numerical Simulation Verification by Experiments for Two to Three Tested DN 150 UFMs
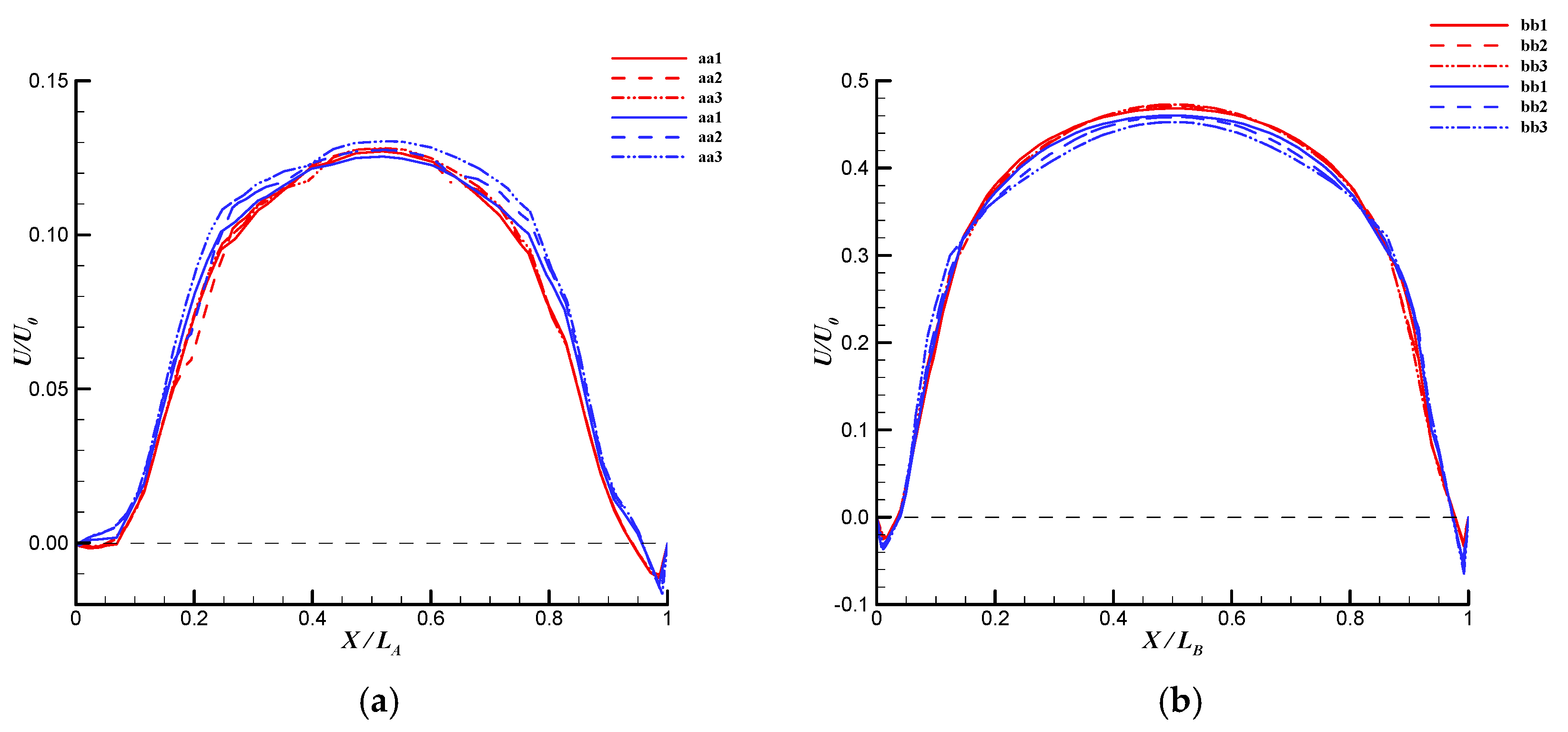
4. Discussion
4.1. Definition and Distribution of Key Factors to Describe Variation in the Velocity Profile
4.2. Flow Analysis for Daniel 3400
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qin, L.; Hu, L.; Mao, K.; Chen, W.; Fu, X. Application of extreme learning machine to gas flow measurement with multipath acoustic transducers. Flow Meas. Instrum. 2016, 49, 31–39. [Google Scholar] [CrossRef]
- Cascetta, F.; Rotondo, G.; Piccato, A.; Spazzini, P. Calibration procedures and uncertainty analysis for a thermal mass gas flowmeter of a new generation. Measurement 2016, 89, 280–287. [Google Scholar] [CrossRef]
- Funck, B.; Baldwin, P. Challenges for Ultrasonic Flow Meters in Wet Gas Applications; FLEXIM GmbH: Berlin, Germany, 2012; p. 21. [Google Scholar]
- Jiang, Z.; Li, C. West to East Gas Transmission Project and Development of China Natural Gass Industry. China Chem. Trade 2017, 9, 6. (In Chinese) [Google Scholar]
- Xie, L. Study on Natural Gas Marketing Strategy of West to East Gas Pipeline Company; Nanjing University: Nanjing, China, 2016. (In Chinese) [Google Scholar]
- National Technical Committee for Measurement of Flowrate and Capacity (China). JJG1030-2007 Verification Regulation of Ultrasonic Flowmeters; General Administration of Quality Supervision, Inspection and Quarantine (China): Beijing, China, 2007.
- Technical Committee ISO/TC 30, ISO 17089-1:2010(en) Measurement of Fluid Flow in Closed Conduits Ultrasonic Meters for Gas: Part 1: Meters for Custody Transfer and Allocation Measurement. 2010. Available online: https://www.iso.org/standard/41235.html (accessed on 3 September 2019).
- Wan, Y. Feasibility analysis of simultaneous verification of gas ultrasonic flowmeter in tightly tandem arrangement. China Metrol. 2012, 119–121. (In Chinese) [Google Scholar] [CrossRef]
- Zheng, D.; Zhang, P.; Xu, T. Study of acoustic transducer protrusion and recess effects on ultrasonic flowmeter measurement by numerical simulation. Flow Meas. Instrum. 2011, 22, 488–493. [Google Scholar] [CrossRef]
- Zhao, H.; Peng, L.; Stephane, S.A.; Ishikawa, H.; Shimizu, K.; Takamoto, M. CFD Aided Investigation of Multipath Ultrasonic Gas Flow Meter Performance Under Complex Flow Profile. IEEE Sens. J. 2014, 14, 897–907. [Google Scholar] [CrossRef]
- Jakevičius, L.; Butkus, J.; Janušas, V.; Ilgarubis, V. The influence of flattened flow profiles to the airflow velocity measurement by ultrasound, Ultragarsas. Ultrasound 2005, 57, 18–21. [Google Scholar]
- Calogirou, A.; Boekhoven, J.; Henkes, R. Effect of wall roughness changes on ultrasonic gas flowmeters. Flow Meas. Instrum. 2001, 12, 219–229. [Google Scholar] [CrossRef]
- Håkansson, E.; Delsing, J. Effects of pulsating flow on an ultrasonic gas flowmeter. Flow Meas. Instrum. 1994, 5, 93–101. [Google Scholar] [CrossRef]
- Yunus, A.C.; Cimbala, J.M. Fluid Mechanics Fundamentals and Applications, International ed.; McGraw Hill Publication: New York, NY, USA, 2006. [Google Scholar]
- Freysa, K.-E.; Lunde, P. A ray theory approach to investigate the influence of flow velocity profiles on transit times in ultrasonic flow meters for gas and liquid. In Proceedings of the 24th Scandinavian Symposium on Physical Acoustics, Ustaoset, Norway, 28–31 January 2001; p. 82. [Google Scholar]
- Yeh, T.T.; Mattingly, G.E. Ultrasonic technology: Prospects for improving flow measurements and standards. In Proceedings of the 10th IMEKO TC9 Conference on Flow Measurement (FLOMEKO 2000), Salvador, Brazil, 4–8 June 2000. [Google Scholar]
- Raisutis, R. Investigation of the flow velocity profile in a metering section of an invasive ultrasonic flowmeter. Flow Meas. Instrum. 2006, 17, 201–206. [Google Scholar] [CrossRef]
- Zanker, K. Diagnostic Ability of the Daniel Four-Path Ultrasonic Flow Meter. In Proceedings of the 2nd International South East Asia Hydrocarbon Flow Measurement Workshop, Kuala Lumpur, Malaysia, 25–28 March 2003. [Google Scholar]
- Zanker, K. Installation effects on single and multi-path ultrasonic meters. In Proceedings of the Flomeko 2000—IMEKO TC9 Conference, Salvador, Brazil, 4–8 June 2000. [Google Scholar]
- Moore, P.I.; Brown, G.J.; Stimpson, B.P. Ultrasonic transit-time flowmeters modelled with theoretical velocity profiles: Methodology. Meas. Sci. Technol. 2000, 11, 1802–1811. [Google Scholar] [CrossRef]
- Furuichi, N.; Terao, Y.; Takamoto, M. Actual flow calibration of a feedwater flowmeter using a high Reynolds number facility at NMIJ. Nucl. Eng. Des. 2009, 239, 1304–1313. [Google Scholar] [CrossRef]






| Model | Path Type | Size | Abscissa | Inclination Angle of Acoustic Paths | Flowrate (m3/h) | Accuracy (%) |
|---|---|---|---|---|---|---|
| Daniel 3400 | Four paths | DN250 | 0.309R (Path B and C) 0.809R (Path A and D) | 60° | 153–5084.96 | 1.0 |
| Straight Length Upstream | Straight Length Downstream | |
|---|---|---|
| Master Meter | 25D | 5D |
| Checking Meter | 25D | 5D |
| Test Meter | 150D | 20D |
| DN250 | 1-UFM1 | 2-UFM1 | 2-UFM2 | 3-UFM1 | 3-UFM2 | 3-UFM3 |
|---|---|---|---|---|---|---|
| CH4 (wt.%) | 94.7567 | 94.7637 | 94.7546 | 94.7589 | 94.7546 | 94.7560 |
| N2 (wt.%) | 1.2633 | 1.2604 | 1.2596 | 1.2600 | 1.2596 | 1.2609 |
| CO2 (wt.%) | 0.7658 | 0.7493 | 0.7599 | 0.7533 | 0.7599 | 0.7644 |
| C2H6 (wt.%) | 2.8918 | 2.9065 | 2.9039 | 2.9084 | 2.9039 | 2.8970 |
| C3H8 (wt.%) | 0.1964 | 0.1949 | 0.1960 | 0.1943 | 0.1960 | 0.1963 |
| P (MPa) | 6.5 | 6.5 | 6.5 | 6.5 | 6.5 | 6.5 |
| T (K) | 293 | 293 | 293 | 293 | 293 | 293 |
| ρ (kg/m3) | 51.278 | 51.268 | 51.277 | 51.272 | 51.277 | 51.279 |
| μ (Pa·s) | 1.2583 | 1.2582 | 1.2583 | 1.2583 | 1.2583 | 1.2583 |
| n-UFMn | A | B | k (Intercept) | Numerical R2 | Experimental Standardized Residual δ* |
|---|---|---|---|---|---|
| 1-UFM1 | −0.427 | 2.037 | 0 | 0.967 | (−1.150~0.732) |
| 2-UFM1 | −0.432 | 2.219 | 0 | 0.962 | (−0.781~0.813) |
| 2-UFM2 | −0.403 | 2.040 | 0 | 0.959 | (−1.531~1.138) |
| 3-UFM1 | −0.325 | 1.416 | 0 | 0.996 | (−0.356~0.342) |
| 3-UFM2 | −0.261 | 1.166 | 0 | 0.951 | (−0.907~1.661) |
| 3-UFM3 | −0.288 | 1.393 | 0 | 0.994 | (−0.636~1.180) |
| 4-UFM1 | −0.307 | 1.584 | 0 | 0.978 | |
| 4-UFM2 | −0.349 | 1.880 | 0 | 0.934 | |
| 4-UFM3 | −0.558 | 3.037 | 0 | 0.853 | |
| 4-UFM4 | −0.520 | 2.680 | 0 | 0.910 | |
| 5-UFM1 | −0.277 | 1.428 | 0 | 0.978 | |
| 5-UFM2 | −0.305 | 1.602 | 0 | 0.968 | |
| 5-UFM3 | −0.367 | 1.984 | 0 | 0.929 | |
| 5-UFM4 | −0.408 | 2.210 | 0 | 0.918 | |
| 5-UFM5 | −0.309 | 1.599 | 1.713 | 0.996 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, T.; Yang, M.; Tu, C.; Huang, Q.; Bao, F.; Yin, Z.; Gao, X. Simultaneous Verification of Multi-Ultrasonic-Flowmeters in Tandem Arrangement for Natural Gas. Appl. Sci. 2019, 9, 3632. https://doi.org/10.3390/app9173632
Hong T, Yang M, Tu C, Huang Q, Bao F, Yin Z, Gao X. Simultaneous Verification of Multi-Ultrasonic-Flowmeters in Tandem Arrangement for Natural Gas. Applied Sciences. 2019; 9(17):3632. https://doi.org/10.3390/app9173632
Chicago/Turabian StyleHong, Tingyang, Meng Yang, Chengxu Tu, Qipeng Huang, Fubing Bao, Zhaoqin Yin, and Xiaoyan Gao. 2019. "Simultaneous Verification of Multi-Ultrasonic-Flowmeters in Tandem Arrangement for Natural Gas" Applied Sciences 9, no. 17: 3632. https://doi.org/10.3390/app9173632
APA StyleHong, T., Yang, M., Tu, C., Huang, Q., Bao, F., Yin, Z., & Gao, X. (2019). Simultaneous Verification of Multi-Ultrasonic-Flowmeters in Tandem Arrangement for Natural Gas. Applied Sciences, 9(17), 3632. https://doi.org/10.3390/app9173632





