Simulation of the Cooling Effect of Porous Asphalt Pavement with Different Air Voids
Abstract
:1. Introduction
2. Specimen Preparation
3. Determination of the Thermophysical Properties of Mixtures
3.1. Specific Heat
3.2. Thermal Conductivity
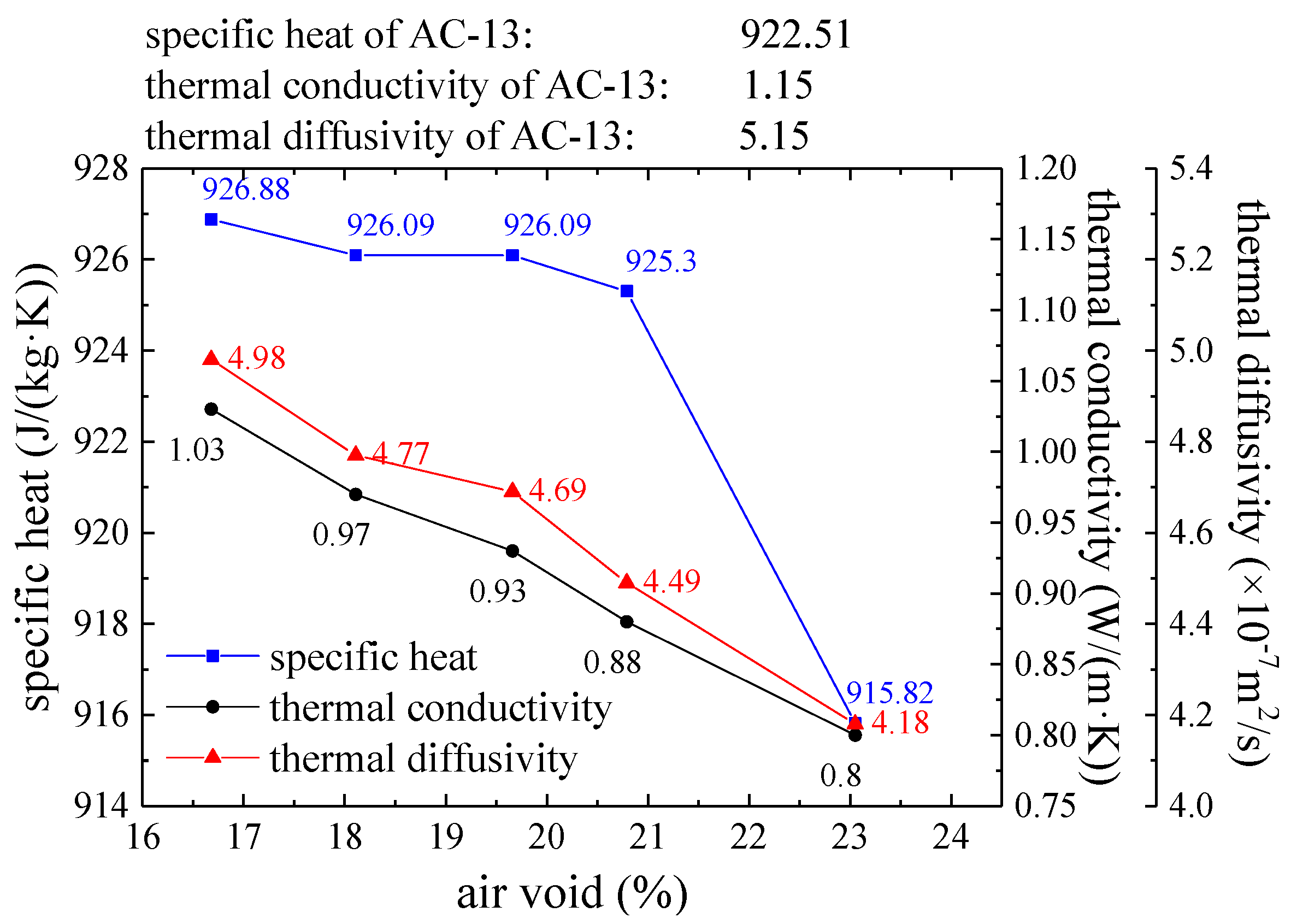
3.3. Thermal Diffusivity
3.4. Data Analysis
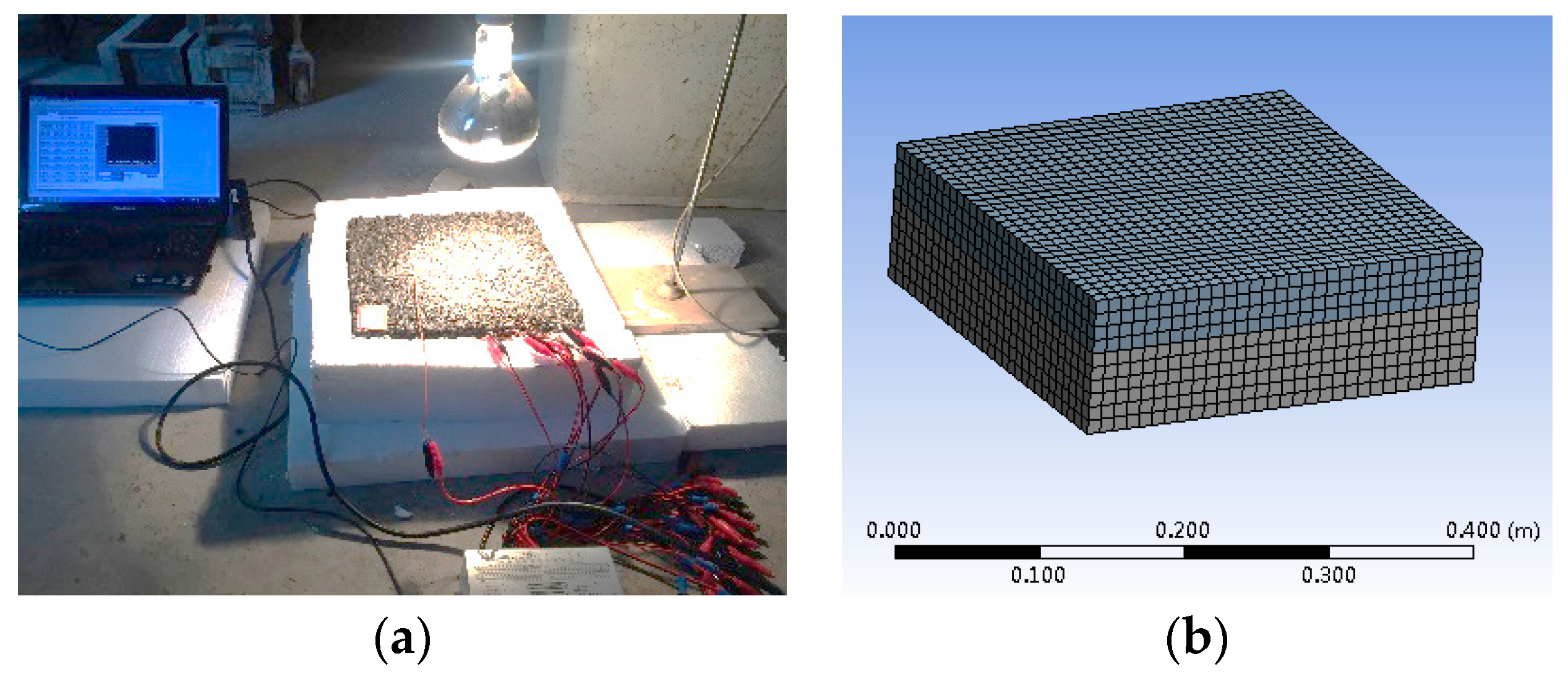
4. Sunshine Experiment
4.1. Simulated Sunshine Experiment under Windless Conditions
4.2. Simulated Sunshine Experiment under Windy Conditions
4.3. Finite Element Virtual Experiment
4.4. Data Analysis
5. Finite Element Simulation of the Pavement Temperature Field
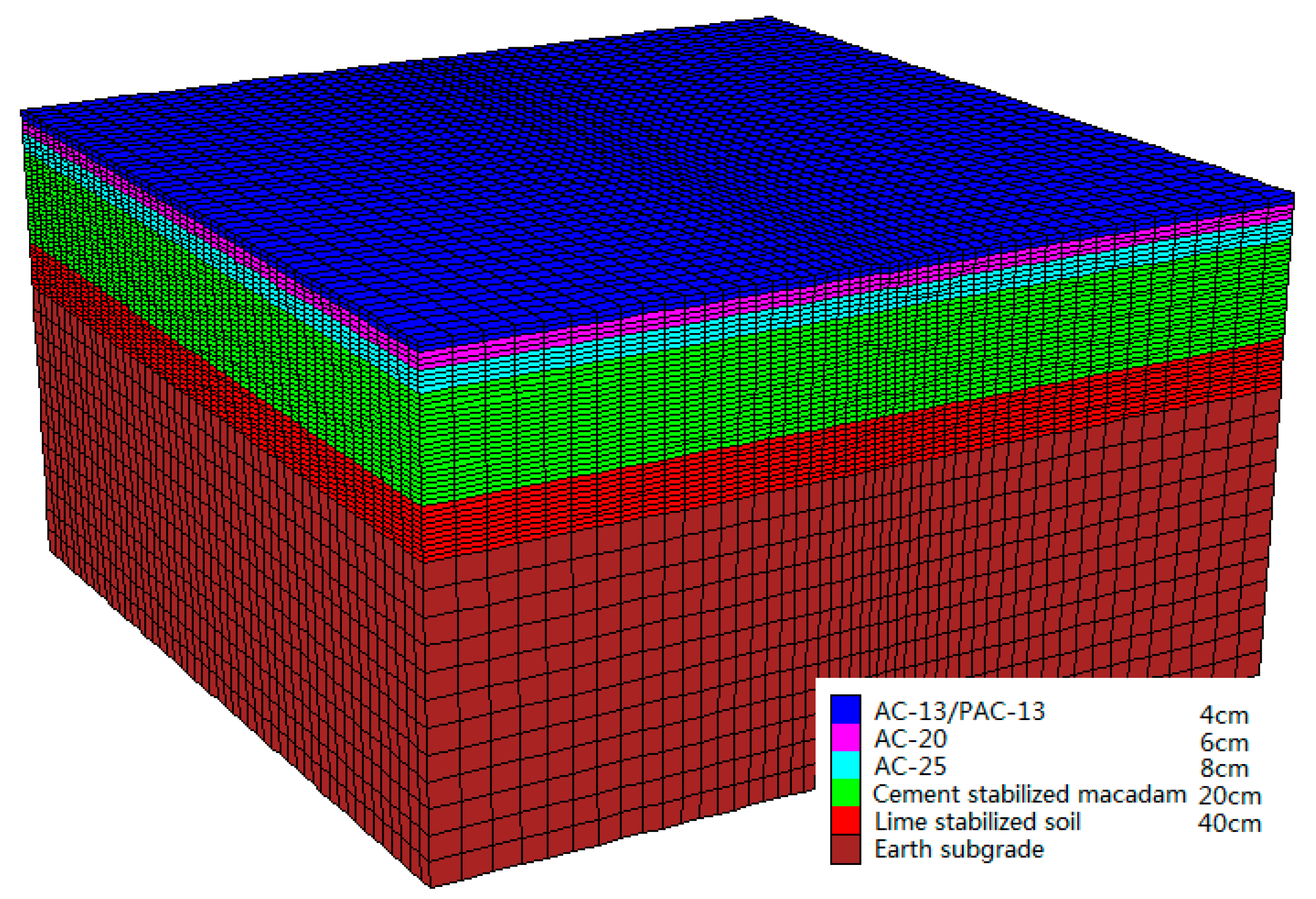
5.1. Model Establishment
5.1.1. Boundary Conditions
5.1.2. Finite Element Model
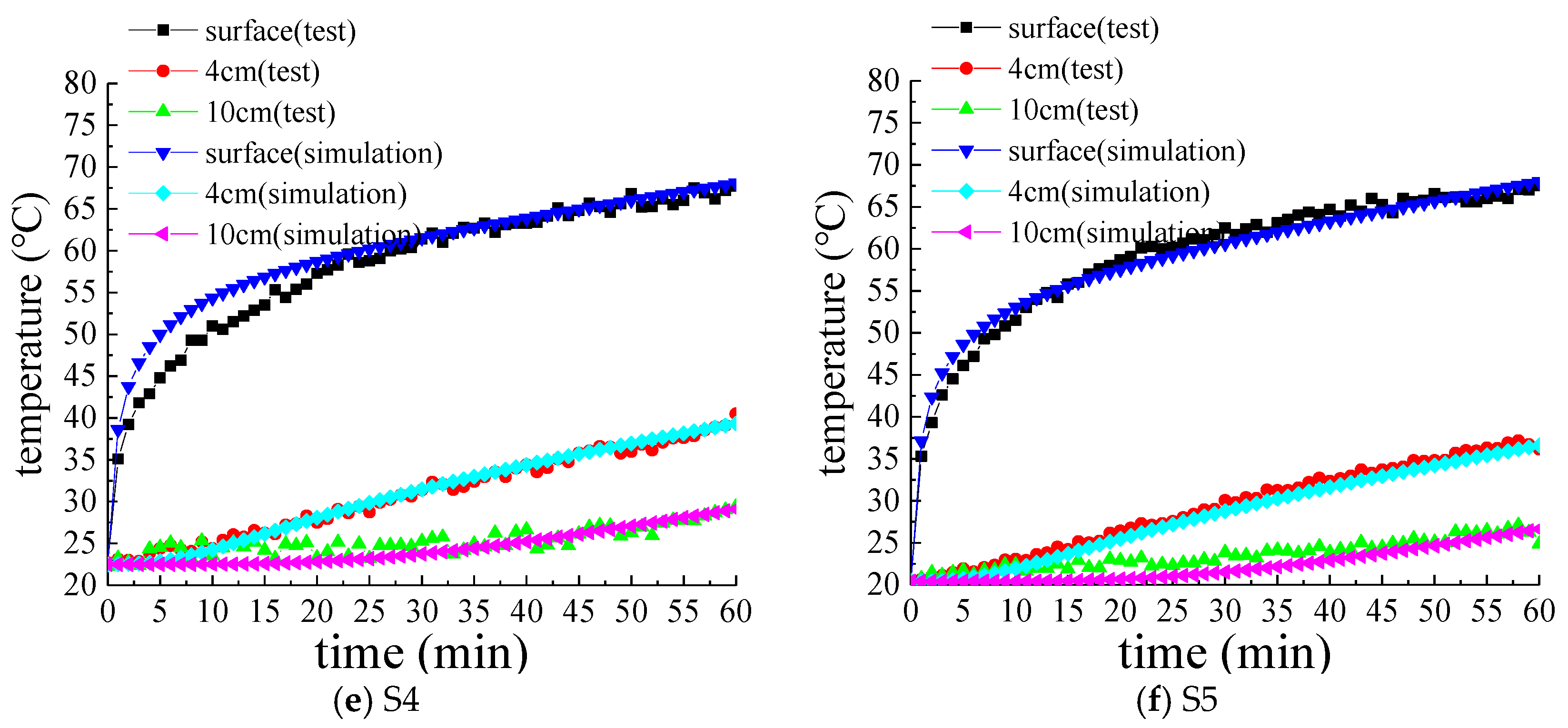
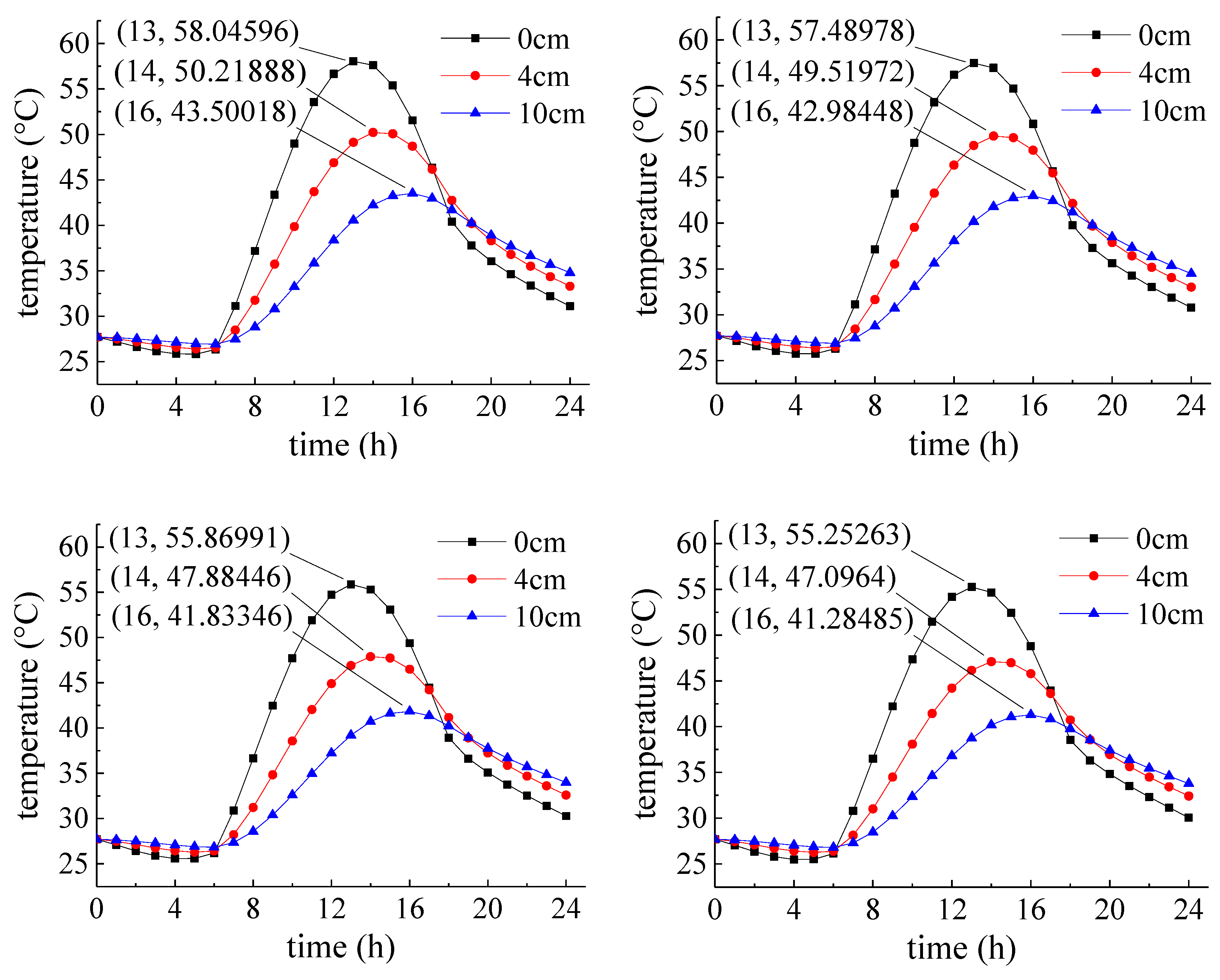
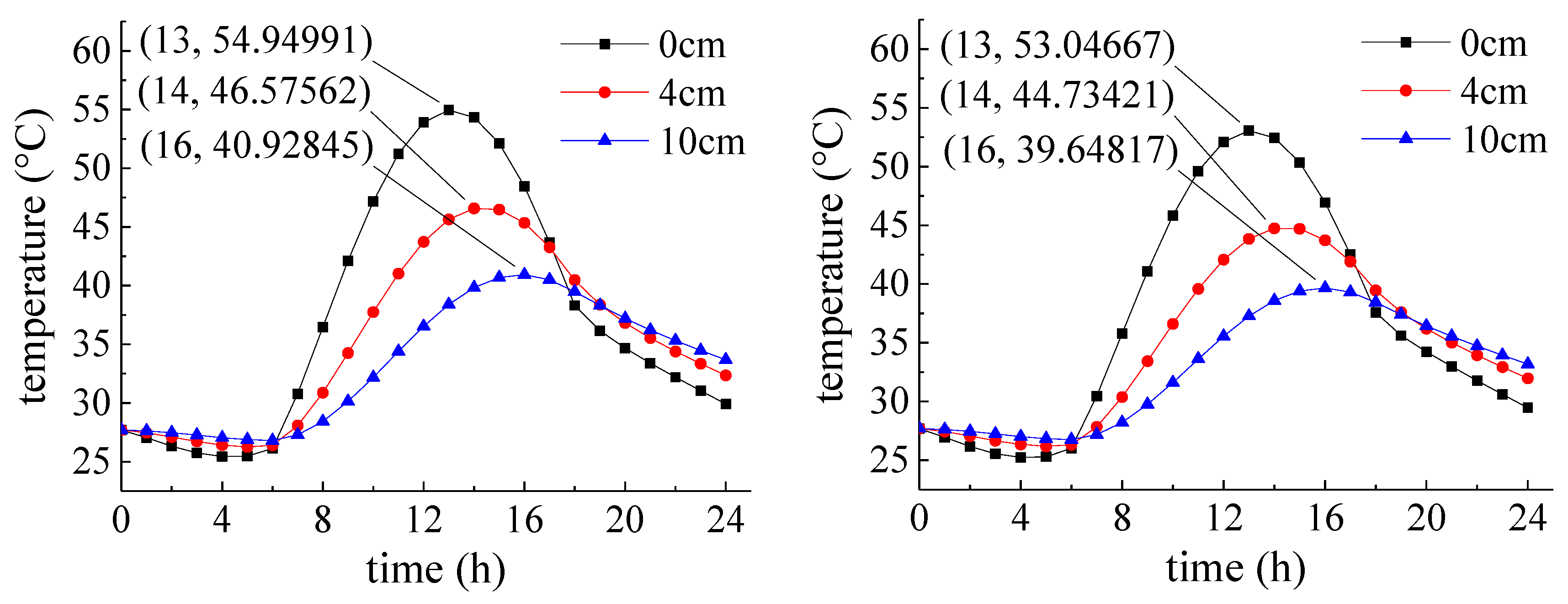
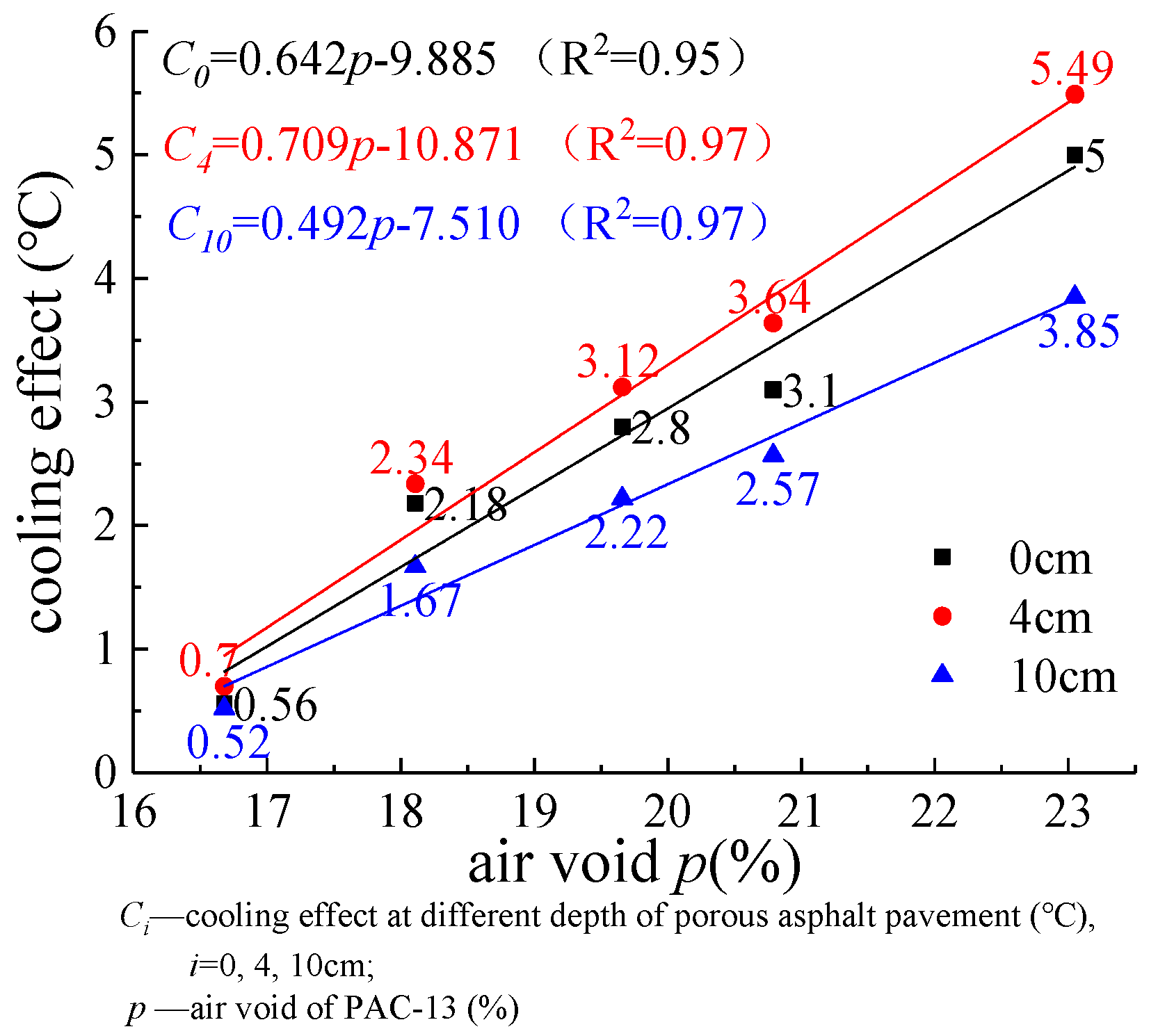
5.2. Finite Element Simulation Result Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Simonsen, E.; Janoo, V.C.; Isacsson, U. Prediction of Pavement Response During Freezing and Thawing Using Finite Element Approach. J. Cold Reg. Eng. 1997, 11, 308–324. [Google Scholar] [CrossRef]
- Shao, X.Z.; Shao, H.M.; Bi, Y.F.; Sun, L.J. Testing Method of Asphalt Mixture Poisson Ratio. J. Tongji Univ. 2006, 34, 1470–1474. [Google Scholar]
- Qin, R.J.; Li, Y.Z.; Li, Z.K. Analyzing the Cause of Asphalt Pavement Rut Damage of Heng-Zao Freeway. In Proceedings of the GeoHunan International Conference, Changsha, Hunan, China, 3–6 August 2009. [Google Scholar]
- Jiang, J.W.; Ni, F.J.; Dong, Q.; Yao, L.Y.; Ma, X. Investigation of the internal structure change of two-layer asphalt mixtures during the wheel tracking test based on 2D image analysis. Constr. Build. Mater. 2019, 209, 66–76. [Google Scholar] [CrossRef]
- Gao, L.; Ni, F.J.; Luo, H.L.; Charmot, S. Characterization of air voids in cold in-place recycling mixtures using x-ray computed tomography. Constr. Build. Mater. 2015, 84, 429–436. [Google Scholar] [CrossRef]
- Hermansson, Å. Simulation model for calculating pavement temperature including maximum temperature. Transport. Res. Rec. 2000, 1699, 134–141. [Google Scholar] [CrossRef]
- Straub, A.L.; Schenck, H.N., Jr.; Przbycien, F.E. Bituminous Pavement Temperature Related to Climate. Highway Res. Rec. 1968, 256, 53–77. [Google Scholar]
- Hermansson, Å. Mathematical model for paved surface summer and winter temperature: Comparison of calculated and measured temperatures. Cold Reg. Sci. Technol. 2004, 40, 1–17. [Google Scholar] [CrossRef]
- Barber, E.S. Calculation of maximum pavement temperature from weather reports. Highway Res. Bd. Bull. 1957, 168, 1–8. [Google Scholar]
- Yan, Z.R. Analysis of the Temperature Field in Layerd Pavement System. J. Tongji Univ. 1984, 3, 76–85. [Google Scholar]
- Liu, C.; Yuan, D. Temperature distribution in layered road structures. J. Transp. Eng. 2000, 126, 93–95. [Google Scholar] [CrossRef]
- Wang, D.; Roesler, J.R. One-dimensional rigid pavement temperature prediction using Laplace transformation. J. Transp. Eng. 2012, 138, 1171–1177. [Google Scholar] [CrossRef]
- Wang, D. Analytical approach to predict temperature profile in a multilayered pavement system based on measured surface temperature data. J. Transp. Eng. 2012, 138, 674–679. [Google Scholar] [CrossRef]
- Chong, W.; Tramontini, R.; Pivoto Specht, L. Application of the Laplace Transform and Its Numerical Inversion to Temperature Profile of a Two-Layer Pavement under Site Conditions. Numer. Heat Tr. A-Appl. 2009, 55, 1004–1018. [Google Scholar] [CrossRef]
- Thanh, D.V.; Feng, C.P. Study on Marshall and Rutting test of SMA at abnormally high temperature. Constr. Build. Mater. 2013, 47, 1337–1341. [Google Scholar] [CrossRef]
- Walubita, L.F.; Faruk Abu, N.M.; Zhang, J.; Hu, X.D.; Lee, S.I. The Hamburg rutting test-Effects of HMA sample sitting time and test temperature variation. Constr. Build. Mater. 2016, 108, 22–28. [Google Scholar] [CrossRef]
- Javilla, B.; Mo, L.T.; Hao, F.; Shu, B.N.; Wu, S.P. Multi-stress loading effect on rutting performance of asphalt mixtures based on wheel tracking testing. Constr. Build. Mater. 2017, 148, 1–9. [Google Scholar] [CrossRef]
- Zheng, Y.X.; Zhang, P.; Liu, H. Correlation between pavement temperature and deflection basin form factors of asphalt pavement. Int. J. Pavement Eng. 2017, 6, 1–10. [Google Scholar] [CrossRef]
- Darabi, M.K.; Huang, C.W.; Bazzaz, M.; Masad, E.A.; Little, D.N. Characterization and validation of the nonlinear viscoelastic-viscoplastic with hardening-relaxation constitutive relationship for asphalt mixtures. Constr. Build. Mater. 2019, 216, 648–660. [Google Scholar] [CrossRef]
- Bazzaz, M.; Darabi, M.K.; Little, D.N.; Garg, N. A straightforward procedure to characterize nonlinear viscoelastic response of asphalt concrete at high temperatures. Transport. Res. Rec. 2018, 2672, 481–492. [Google Scholar] [CrossRef]
- Bazzaz, M. Experimental and Analytical Procedures to Characterize Mechanical Properties of Asphalt Concrete Materials for Airfield Pavement Applications. Ph.D. Thesis, University of Kansas, Lawrence, KS, USA, 2018; p. 247. [Google Scholar]
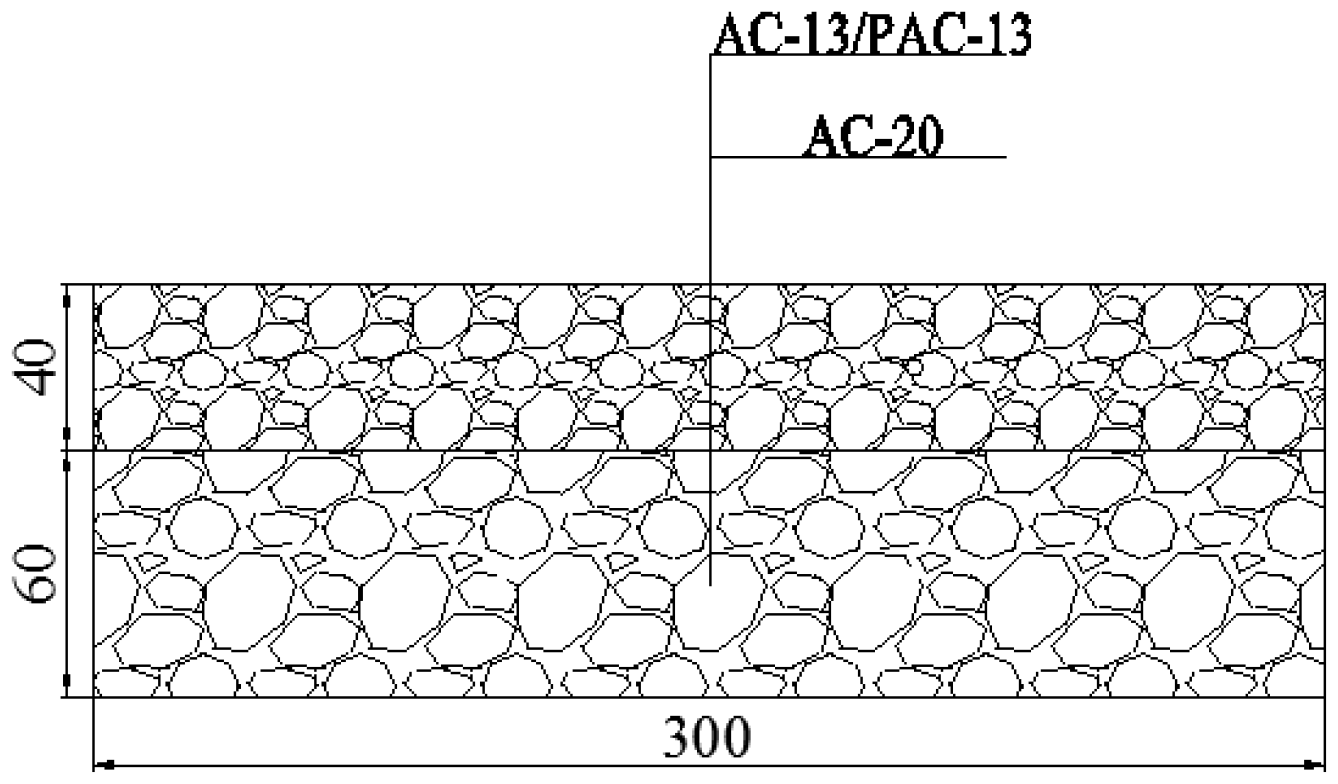


| Sieve Size (mm) | Recommended Gradation (%) | PAC-13 Gradation (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Upper Limit | Lower Limit | Median | 1 | 2 | 3 | 4 | 5 | |
| 16 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 13.2 | 100 | 90 | 95 | 95 | 95 | 95 | 92.7 | 95 |
| 9.5 | 71 | 40 | 55.5 | 70 | 67.5 | 65 | 56.8 | 45 |
| 4.75 | 30 | 10 | 20 | 28 | 26.5 | 25 | 16.7 | 10 |
| 2.36 | 22 | 8 | 15 | 21 | 18.5 | 16 | 10.4 | 8 |
| 1.18 | 18 | 6 | 12 | 14.5 | 14.3 | 14 | 7.9 | 7 |
| 0.6 | 14 | 4 | 9 | 10.5 | 10 | 11 | 6.6 | 6 |
| 0.3 | 12 | 3 | 7.5 | 9 | 8 | 9 | 5.2 | 5 |
| 0.15 | 9 | 3 | 6 | 6 | 6 | 6 | 4.5 | 4 |
| 0.075 | 7 | 3 | 5 | 4 | 4 | 4 | 3.8 | 3 |
| Air Voids (%) | 16.68 | 18.11 | 19.66 | 20.79 | 23.05 | |||
| Specimen Type | Upper-Layer Material (air voids) | Lower-Layer Material | Specimen Number |
|---|---|---|---|
| 4 cm AC-13 + 6 cm AC-20 | AC-13 | AC-20 | AC |
| 4 cm PAC-13 + 6 cm AC-20 | PAC-13 (16.68%) | AC-20 | S1 |
| PAC-13 (18.11%) | AC-20 | S2 | |
| PAC-13 (19.66%) | AC-20 | S3 | |
| PAC-13 (20.79%) | AC-20 | S4 | |
| PAC-13 (23.05%) | AC-20 | S5 |
| Specimen Number | Upper-Layer Air Voids (Material) | Lower-Layer Material | Equilibrium Temperature (°C) | ||
|---|---|---|---|---|---|
| Surface | 4 cm | 10 cm | |||
| AC | AC-13 | AC-20 | 65.6 | 41.3 | 30.3 |
| S1 | 16.68% (PAC-13) | AC-20 | 64.8 | 40 | 29.2 |
| S2 | 18.11% (PAC-13) | AC-20 | 67.4 | 41.3 | 28.9 |
| S3 | 19.66% (PAC-13) | AC-20 | 66.45 | 39.3 | 28.8 |
| S4 | 20.79% (PAC-13) | AC-20 | 67.2 | 38.8 | 28.6 |
| S5 | 23.05% (PAC-13) | AC-20 | 67.5 | 37.15 | 27.86 |
| Specimen Number | Upper Layer Air Void (Material) | Lower Layer Material | Surface Equilibrium Temperature (°C) | Convective Heat Transfer Coefficient (W·m-2·°C-1) |
|---|---|---|---|---|
| AC | AC-13 | AC-20 | 28.5 | 19.058 |
| S1 | 16.68% (PAC-13) | AC-20 | 28.2 | 20.642 |
| S2 | 18.11% (PAC-13) | AC-20 | 27.8 | 24.639 |
| S3 | 19.66% (PAC-13) | AC-20 | 27.4 | 26.551 |
| S4 | 20.79% (PAC-13) | AC-20 | 27.5 | 27.639 |
| S5 | 23.05% (PAC-13) | AC-20 | 26.6 | 34.148 |
| Material | Density (kg/m³) | Specific Heat (J·kg−1·°C−1) | Thermal Conductivity (J·m−1·h−1·°C−1) |
|---|---|---|---|
| AC25 | 2300 | 924.9 | 1.3 |
| Cement-stabilized macadam | 2200 | 911.7 | 1.56 |
| Lime-stabilized soil | 2100 | 942.9 | 1.43 |
| Earth Subgrade | 1800 | 1040 | 1.56 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Wang, Z.; Xie, J.; Liu, Y.; Jia, S. Simulation of the Cooling Effect of Porous Asphalt Pavement with Different Air Voids. Appl. Sci. 2019, 9, 3659. https://doi.org/10.3390/app9183659
Gao L, Wang Z, Xie J, Liu Y, Jia S. Simulation of the Cooling Effect of Porous Asphalt Pavement with Different Air Voids. Applied Sciences. 2019; 9(18):3659. https://doi.org/10.3390/app9183659
Chicago/Turabian StyleGao, Lei, Zhanqi Wang, Jianguang Xie, Yanping Liu, and Sicheng Jia. 2019. "Simulation of the Cooling Effect of Porous Asphalt Pavement with Different Air Voids" Applied Sciences 9, no. 18: 3659. https://doi.org/10.3390/app9183659
APA StyleGao, L., Wang, Z., Xie, J., Liu, Y., & Jia, S. (2019). Simulation of the Cooling Effect of Porous Asphalt Pavement with Different Air Voids. Applied Sciences, 9(18), 3659. https://doi.org/10.3390/app9183659





