Construction and Numerical Realization of a Magnetization Model for a Magnetostrictive Actuator Based on a Free Energy Hysteresis Model
Abstract
:Featured Application
Abstract
1. Introduction
2. Magnetostrictive Mechanism of the Giant Magnetostrictive Material and Its Modeling Method
2.1. Ferromagnetic Properties of Material and Their Magnetostrictive Mechanisms
2.2. Factors Affecting Magnetic Coupling Characteristics of Giant Magnetostrictive Material
2.3. Comparative Study of Hysteresis Models of Giant Magnetostrictive Actuators
3. Construction of a Hysteresis Model of a Giant Magnetostrictive Microactuator Based on Free Energy
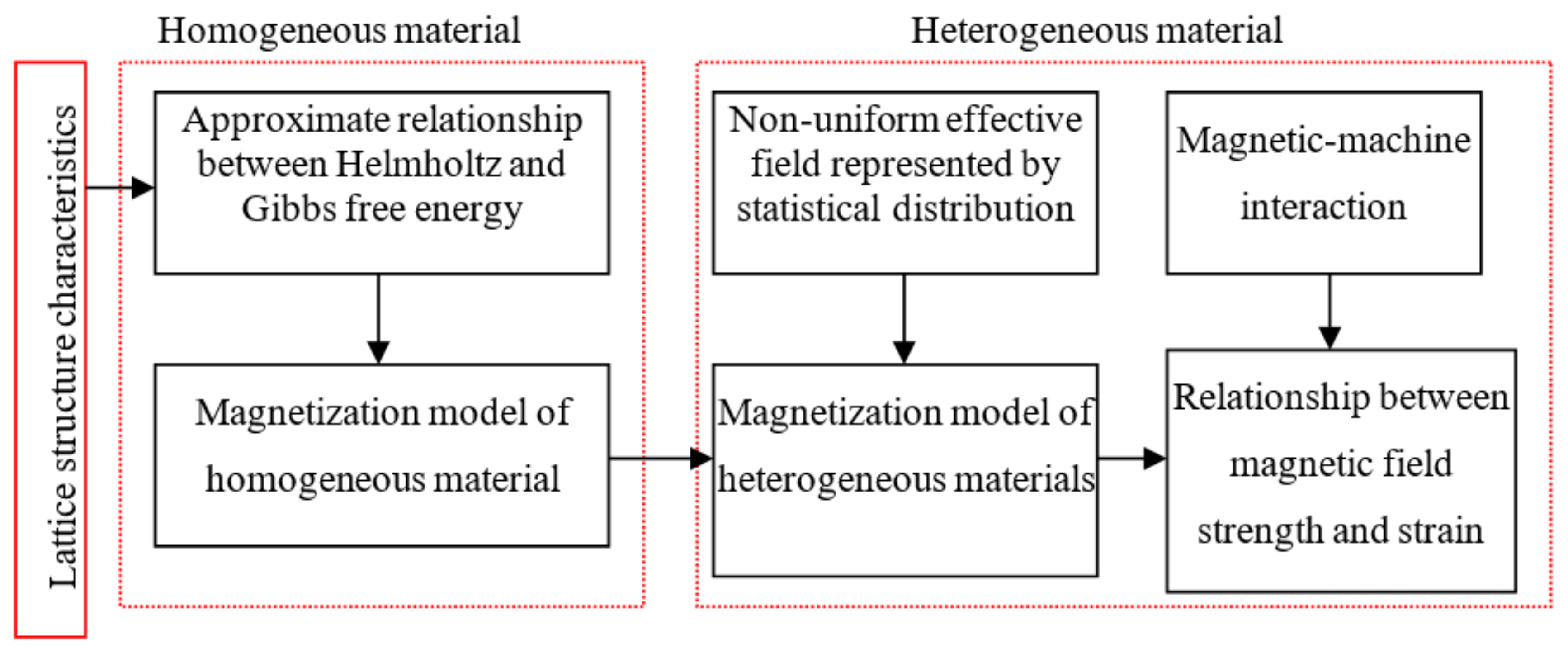
3.1. Research Process Based on the Free Energy Hysteresis Model
3.2. Theoretical Basis for the Establishment of the Free Energy Hysteresis Model
4. Numerical Implementation of a Magnetization Model Based on the Free Energy Hysteresis Model
4.1. Discretization of Integrals
4.2. Kernel Function Implementation
4.3. Verification Based on the Free Energy Hysteresis Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jia, Z.Y.; Wang, F.J.; Guo, D.M. Functional Material Driving Microactutor and Its Key Technology. Chin. J. Mech. Eng. 2003, 39, 61–67. [Google Scholar] [CrossRef]
- Lu, Q.G. Development and application of micro actuation technology. J. Nanchang Inst. 2008, 12, 1–6. [Google Scholar]
- Park, G.; Bement, M.T.; Hartman, D.A.; Smith, R.E.; Farrar, C.R. The use of active materials for machining processs: A review. Int. J. Mach. Tools Manuf. 2007, 47, 2189–2206. [Google Scholar] [CrossRef]
- Liang, S.Y.; Hecker, R.L.; Landers, R.G. Machining process monitoring and control: The state of the art, ASME. J. Manuf. Sci. Eng. 2004, 126, 297–310. [Google Scholar] [CrossRef]
- Inman, D.J. Smart materials in damage detection and prognosis. In Proceedings of the Fifth International Conference on Damage Assessment of Structures, Southampton, UK, 1–3 July 2003; pp. 3–16. [Google Scholar]
- Maffiodo, D.; Raparelli, T. Flexible Fingers Based on Shape Memory Alloy Actuated Modules. Machines 2019, 7, 36–40. [Google Scholar] [CrossRef]
- Khan, M.M.; Lagoudas, D.C.; Rediniotis, O.K. Thermoelectric SMA actuator: Preliminary prototype testing. Proc. Spie-Int. Soc. Opt. Eng. 2004, 113, 94–99. [Google Scholar]
- Ohmata, K.; Zaike, M.; Koh, T. A Three-link Arm Type Vibration Control Device Using Magnetostrictive Actuators. J. Alloy. Compd. 1997, 258, 74–78. [Google Scholar] [CrossRef]
- Wakiwaka, H.; Aoki, K.; Yoshikawa, T.; Kamata, H.; Igarashi, M.; Yamada, H. Maximum output of a low frequency sound source using giant magnetostrictive material. J. Alloy. Compd. 1997, 258, 87–92. [Google Scholar] [CrossRef]
- Jenner, A.G.; Smith, R.J.E.; Wilkinson, A.J. Actuation and transduction giant magnetostrictive alloys. Mechatronics 2000, 10, 457–466. [Google Scholar] [CrossRef]
- Li, Q.; Ye, Z.; Meng, Y.; Tian, Y.; Wen, S. Linear inchworm mechanism based on giant magnetostrictive and piezoelectric materials. J. Tsinghua Univ. (Sci. Technol.) 2005, 45, 1055–1057. [Google Scholar]
- Clark, A.E. Magnetostrictive Rare Earth-Fe2 Compounds; Wohlfarh, E.P., Ed.; North-Holland Publishing Company: New York, NY, USA, 1980. [Google Scholar]
- Benbouzid, M.E.H.; Reyne, G.; Meunier, G.; Kvarnsjo, L.; Engdahl, G. Dynamic modelling of giant magnetostriction in Terfenol-D rods by the finite element method. IEEE Trans. Magn. 1995, 31, 1821–1824. [Google Scholar] [CrossRef]
- Azoum, K.; Besbes, M.; Bouillault, F. 3D FEM of magnetostriction phenomena using coupled constitutive laws. Int. J. Appl. Electromagn. Mech. 2004, 19, 367–371. [Google Scholar] [CrossRef]
- Benatar, J.G. Fem implementations of magnetostrictive-based applications. Master’s Thesis, University Of Maryland, College Park, MD, USA, 2005. [Google Scholar]
- Zhao, Z.; Wu, Y.; Gu, X. Three-dimensional nonlinear dynamic finite element model for giant magnetostrictive actuators. J. Zhgenjiang Univ. (Eng. Sci.) 2008, 2, 203–208. [Google Scholar]
- Zhong, W.-D. Ferromagnetics (Version 2); Science Press: Beijing, China, 1992. [Google Scholar]
- De Lacheisserie, E.D.T. Magnetostriction Theory and Applications of Magnetoelasticity; CRC Press, Inc.: Boca Raton, FL, USA, 1993. [Google Scholar]
- Wang, S.; Wan, F.; Zhao, H.; Chen, W.; Zhang, W.; Zhou, Q. A Sensitivity-enhanced Fiber Grating Current Sensor Based on Giant Magnetostrictive Material for Large-Current Measurement. Sensors 2019, 19, 1755. [Google Scholar] [CrossRef]
- Mcmaster, O.D.; Verhoeven, J.B.; Gibson, E.D. Preparation of Terfenol-D by Float Zone Solidification. J. Magn. Magn. Mater. 1986, 54, 849–851. [Google Scholar] [CrossRef]
- Tang, X.; Miao, Y.; Chen, X.; Nie, B. A Flexible and Highly Sensitive Inductive Pressure Sensor Array Based on Ferrite Films. Sensors 2019, 19, 2406. [Google Scholar] [CrossRef]
- Greenough, R.D.; Sehulze, M.P.; Pollard, D. Non-destructive testing of Terfenol-D. J. Alloy. Compd. 1997, 258, 118–122. [Google Scholar] [CrossRef]
- Claeyssen, F.; Lhermet, N.; Le Letty, R.; Bouchilloux, P. Actuators transducers and motors based on giant magnetostrictive materials. J. Alloy. Compd. 1997, 258, 61–73. [Google Scholar] [CrossRef]
- Moffett, M.B.; Clark, A.E.; Wun-Fogle, M.; Linberg, J.; Teter, J.P.; McLaughlin, E.A. Characterization of Terfenol-D for magnetostrictive transucers. J. Acoust. Soc. Am. 1991, 89, 1448–1455. [Google Scholar] [CrossRef]
- MOHRI, K. Factors Affecting the Output Voltage of a Magnetostrictive Torque Sensor Constructed from Ni-Fe Sputtered Films and a Ti-Alloy Shaft. Jpn. Appl. Magn. Soc. 1998, 22, 1074–1079. [Google Scholar]
- Hall, A.; Coatney, M.; Bradley, N.; Hyeong Yoo, J.; Jones, N.; Williams, B.; Myers, O. Nondestructive Damage Detection of a Magnetostrictive Composite Structure. Proceedings 2018, 2, 416. [Google Scholar] [CrossRef]
- Stovner, B.N.; Johansen, T.A.; Schjølberg, I. Globally exponentially stable filters for underwater position estimation using an array of hydroacoustic transducers on the vehicle and a single transponder. Ocean Eng. 2018, 155, 351–360. [Google Scholar] [CrossRef]
- Clark, A.E.; Teter, J.P.; McMasters, D. Magnetostriction jumps in twined Tb0.3Dy0.7Fe1.9. J. Appl. Phys. 1988, 63, 3910–3912. [Google Scholar] [CrossRef]
- Choudhary, P.; Meydan, T. A novel aceelerometer design using the inverse magnetostrictive effect. Sens. Actuators 1997, 59, 51–55. [Google Scholar] [CrossRef]
- Ishihara, S. High Precision Positioning for Submicron Lithography Bull. Jpn. Soc. Pree 1987, 21, 1–8. [Google Scholar]
- Tatevosyan, A.S.; Tatevosyan, A.A.; Zaharova, N.V. The Study of the Electrical Steel and Amorphous Ferromagnets Magnetic Properties. Procedia Eng. 2016, 152, 727–734. [Google Scholar] [CrossRef]
- Apicella, V.; Clemente, C.S.; Davino, D.; Leone, D.; Visone, C. Review of Modeling and Control of Magnetostrictive Actuators. Actuators 2019, 8, 45. [Google Scholar] [CrossRef]
- Iyer, R.V.; Tan, X.; Krishnaprasad, P.S. Approximate Inversion of the Preisach Hysteresis Operator with Application to Control of Smart Actuators. IEEE Trans. Autom. Control 2005, 50, 798–810. [Google Scholar] [CrossRef]
- Tan, X.; Baras, J.S.; Krishnaprasad, P.S. A dynamic model for magnetostrictive hysteresis. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 2, pp. 1074–1079. [Google Scholar]
- Mayergoyz, I.D.; Friedman, G. Generalized Preisach Model of Hysteresis. IEEE Trans. Magn. 1988, 24, 212–217. [Google Scholar] [CrossRef]
- Della Torre, E. Preisach modeling and reversible magnetization. IEEE Trans. Magn. 1990, 26, 3052–3058. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Li, Y.; Li, S.; Li, H.; Wang, W. Comparative Investigation of Phenomenological Modeling for Hysteresis Responses of Magnetorheological Elastomer Devices. Int. J. Mol. Sci. 2019, 20, 3216. [Google Scholar] [CrossRef]
- Jiles, D.C. Introduction to Magnetism and Magnetic Materials; Chapman and Hall: London, UK, 1995. [Google Scholar]
- Dapino, M.J.; Smith, R.C.; Flatau, A.B. Structural Magnetic Strain Model for Magneto-strictive Transducers. IEEE Trans. Magn. 2000, 36, 545–556. [Google Scholar] [CrossRef]
- Smith, R.C.; Dapino, M.J.; Seelecke, S. Free energy model for hysteresis in magnetostrictive transducers. J. Appl. Phys. 2003, 93, 458–466. [Google Scholar] [CrossRef] [Green Version]
- Smith Ralph, C.; Dapino Marcelo, J.; Braun Thomas, R.; Mortensen Anthony, P. A homogenized energy framework for ferromagnetic hysteresis. IEEE Trans. Magn. 2006, 42, 1747–1769. [Google Scholar] [CrossRef]
- Smith, R.C.; Seelecke, S.; Dapino, M.; Ounaies, Z. A unified framework for modeling hysteresis in ferroic materials. J. Mech. Phys. Solids 2006, 54, 6–85. [Google Scholar] [CrossRef]
- Xiao, Y.; Gou, X.F.; Zhang, D.G. A one-dimension nonlinear hysteretic constitutive model with elasto-thermo-magnetic coupling for giant magnetostrictivematerials. J. Magn. Magn. Mater. 2017, 441, 642–649. [Google Scholar] [CrossRef]








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Zhang, C.-y.; Yu, J.-x.; Dang, Z.; Zhou, M. Construction and Numerical Realization of a Magnetization Model for a Magnetostrictive Actuator Based on a Free Energy Hysteresis Model. Appl. Sci. 2019, 9, 3691. https://doi.org/10.3390/app9183691
Yu Z, Zhang C-y, Yu J-x, Dang Z, Zhou M. Construction and Numerical Realization of a Magnetization Model for a Magnetostrictive Actuator Based on a Free Energy Hysteresis Model. Applied Sciences. 2019; 9(18):3691. https://doi.org/10.3390/app9183691
Chicago/Turabian StyleYu, Zhen, Chen-yang Zhang, Jing-xian Yu, Zhang Dang, and Min Zhou. 2019. "Construction and Numerical Realization of a Magnetization Model for a Magnetostrictive Actuator Based on a Free Energy Hysteresis Model" Applied Sciences 9, no. 18: 3691. https://doi.org/10.3390/app9183691




