MPC for Optimized Energy Exchange between Two Renewable-Energy Prosumers
Abstract
1. Introduction
1.1. Microgrids
1.2. Outline and Scope of This Work
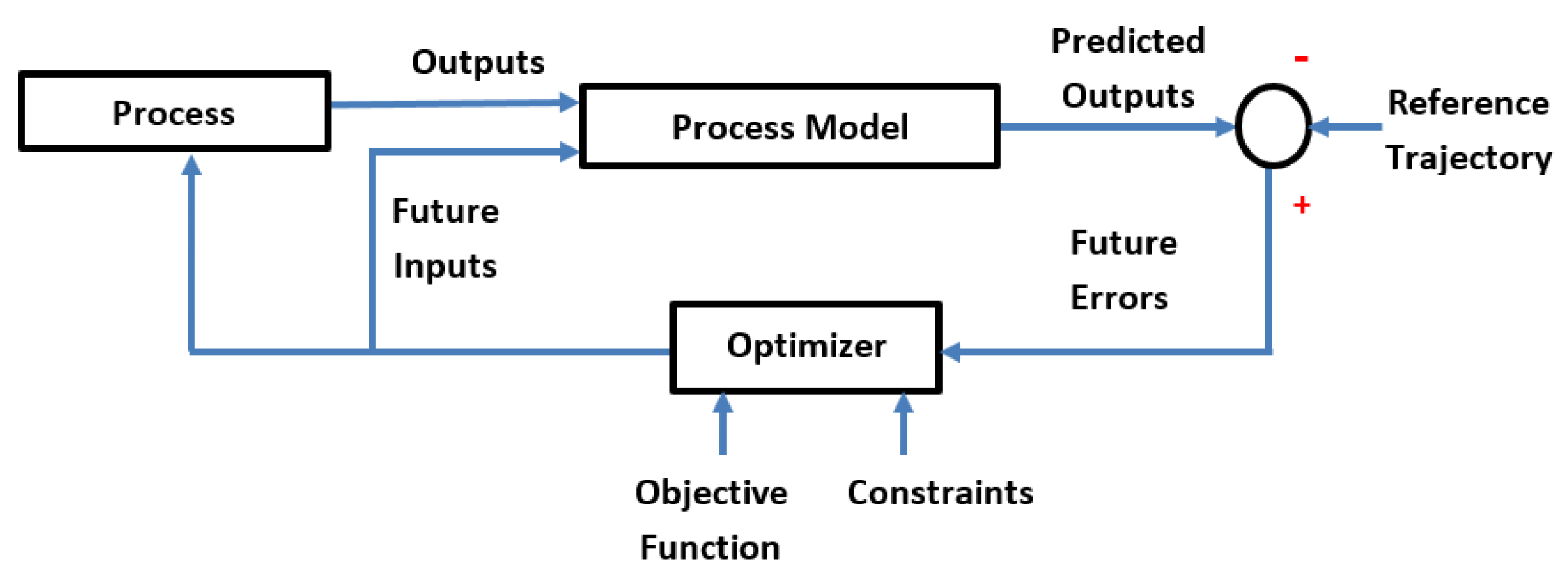
1.3. Model Productive Control
1.4. Case Study
2. Problem Formulation
2.1. Battery Storage
2.2. State-Space Formulation
2.3. MPC Objective Function and Reference Trajectory
2.4. System Constraints
2.5. MPC Algorithm
3. Simulation Results
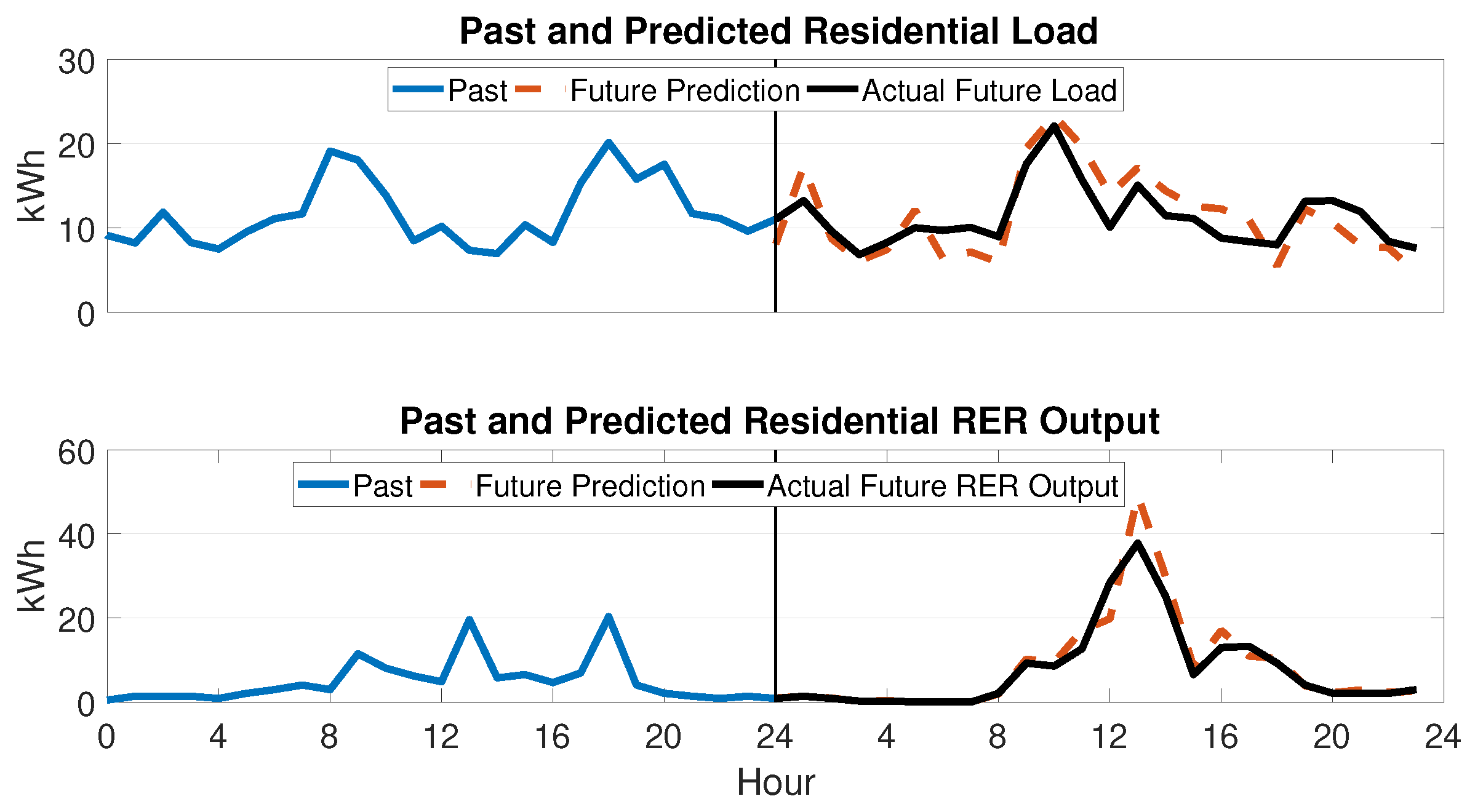
3.1. Load and Supply Forecasting
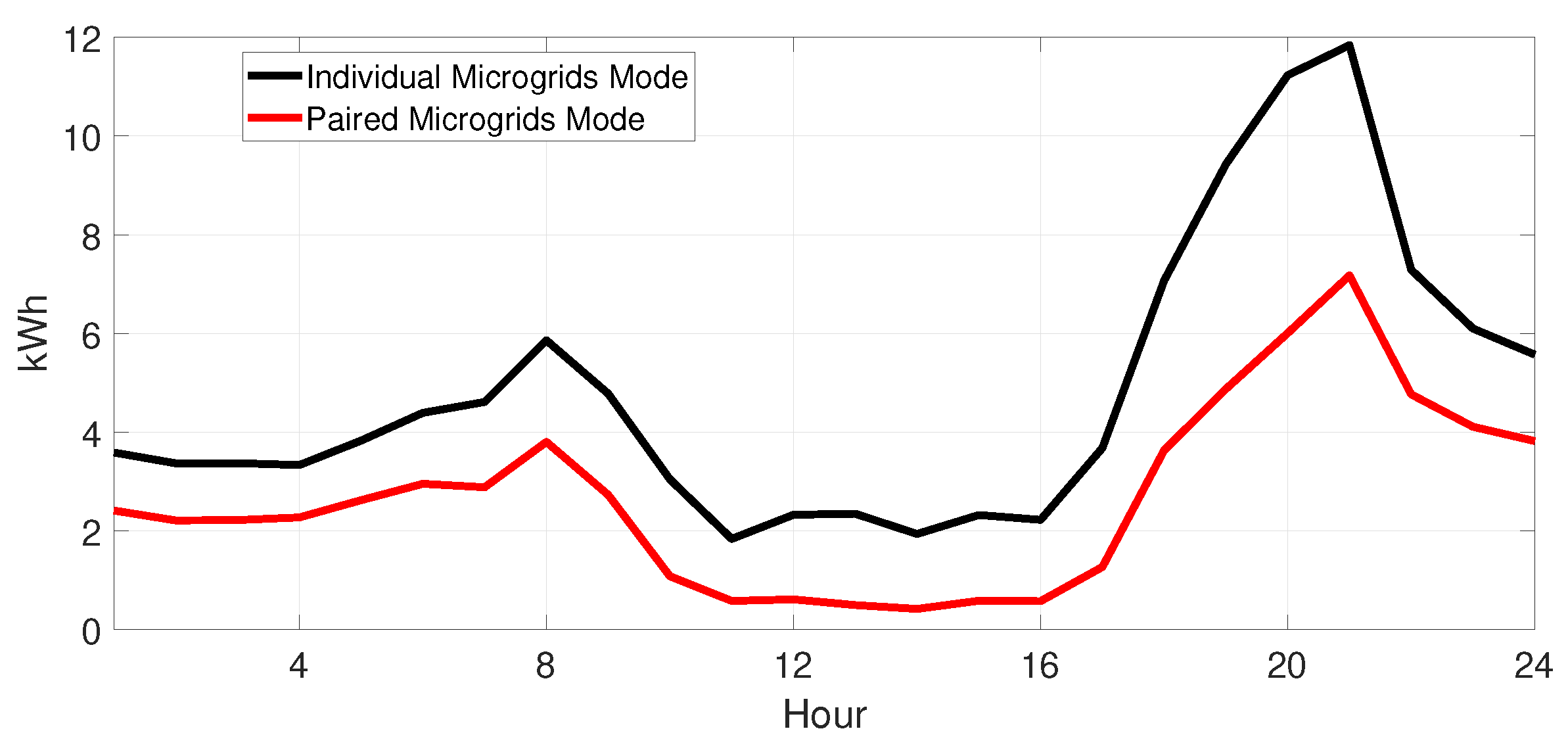
3.2. Performance Benefit of Prosumer Pairing
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Booth, S.; Barnett, J.; Burman, K.; Hambrick, J.; Westby, R. Net Zero Energy Military Installations: A Guide to Assessment and Planning; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010. [Google Scholar]
- Mylrea, M.; Gourisetti, S.N.G. Blockchain for Smart Grid Resilience: Exchanging Distributed Energy at Speed, Scale and Security. In Proceedings of the Resilience Week (RWS), Wilmington, DE, USA, 18–22 September 2017; pp. 18–23. [Google Scholar]
- Washom, B.; Dilliot, J.; Weil, D.; Kleissl, J.; Balac, N.; Torre, W.; Richter, C. Ivory tower of power: Microgrid implementation at the University of California, San Diego. IEEE Power Energy Mag. 2013, 11, 28–32. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Bizon, N. Optimal operation of fuel cell/wind turbine hybrid power system under turbulent wind and variable load. Appl. Energy 2018, 212, 196–209. [Google Scholar] [CrossRef]
- Aldaouab, I.; Daniels, M.; Hallinan, K. Microgrid Cost Optimization for a Mixed-Use Building. In Proceedings of the Power and Energy Conference (TPEC), College Station, TX, USA, 9–10 February 2017; pp. 1–5. [Google Scholar]
- Palma-Behnke, R.; Benavides, C.; Lanas, F.; Severino, B.; Reyes, L.; Llanos, J.; Sáez, D. A microgrid energy management system based on the rolling horizon strategy. IEEE Trans. Smart Grid 2013, 4, 996–1006. [Google Scholar] [CrossRef]
- Aldaouab, I.; Daniels, M. Renewable Energy Dispatch Control Algorithms for a Mixed-Use Building. In Proceedings of the Green Energy and Smart Systems Conference (IGESSC), Long Beach, CA, USA, 6–7 November 2017; pp. 1–5. [Google Scholar]
- Aldaouab, I.; Daniels, M.; Ordóñez, R. Model Predictive Control Energy Dispatch to Optimize Renewable Penetration for a Microgrid with Battery and Thermal Storage. In Proceedings of the Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar]
- Atzori, M. Blockchain Technology and Decentralized Governance: Is the State Still Necessary? SSRN: Rochester, NY, USA, 2015. [Google Scholar]
- Peck, M.E.; Wagman, D. Energy trading for fun and profit buy your neighbor’s rooftop solar power or sell your own-it’ll all be on a blockchain. IEEE Spectr. 2017, 54, 56–61. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Long, C.; Cheng, M. Review of existing peer-to-peer energy trading projects. Energy Procedia 2017, 105, 2563–2568. [Google Scholar] [CrossRef]
- Zhou, Y.; Ci, S.; Li, H.; Yang, Y. A New Framework for Peer-to-Peer Energy Sharing and Coordination in the Energy Internet. In Proceedings of the Communications (ICC)—2017 IEEE International Conference on IEEE, Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy-sharing model with price-based demand response for microgrids of peer-to-peer prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
- Ouammi, A.; Dagdougui, H.; Dessaint, L.; Sacile, R. Coordinated model predictive-based power flows control in a cooperative network of smart microgrids. IEEE Trans. Smart Grid 2015, 6, 2233–2244. [Google Scholar] [CrossRef]
- Parisio, A.; Rikos, E.; Glielmo, L. A model predictive control approach to microgrid operation optimization. IEEE Trans. Control. Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Camacho, E.F.; Alba, C.B. Model Predictive Control; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Shadmand, M.B.; Balog, R.S.; Abu-Rub, H. Model predictive control of PV sources in a smart DC distribution system: Maximum power point tracking and droop control. IEEE Trans. Energy Convers. 2014, 29, 913–921. [Google Scholar] [CrossRef]
- Hooshmand, A.; Malki, H.A.; Mohammadpour, J. Power flow management of microgrid networks using model predictive control. Comput. Math. Appl. 2012, 64, 869–876. [Google Scholar] [CrossRef]
- Oldewurtel, F.; Parisio, A.; Jones, C.N.; Gyalistras, D.; Gwerder, M.; Stauch, V.; Lehmann, B.; Morari, M. Use of model predictive control and weather forecasts for energy efficient building climate control. Energy Build. 2012, 45, 15–27. [Google Scholar] [CrossRef]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB®; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]




| System Outputs | Objective Function Terms | Description |
|---|---|---|
| Energy purchased from other network | ||
| prosumers or retail suppliers | ||
| Charging and discharging energy | ||
| transfer to battery | ||
| Energy sold to other network prosumers | ||
| Energy transferred from the residential renewable energy resource (RER) | ||
| supply to the commercial load and vice versa | ||
| Energy transferred from the residential | ||
| battery to the commercial load and vice versa |
| Unpaired | Paired | |
|---|---|---|
| Percentage of both loads satisfied by RER production | 71% | 84% |
| Percentage of total RER output transferred to other prosumers | 39% | 32% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldaouab, I.; Daniels, M.; Ordóñez, R. MPC for Optimized Energy Exchange between Two Renewable-Energy Prosumers. Appl. Sci. 2019, 9, 3709. https://doi.org/10.3390/app9183709
Aldaouab I, Daniels M, Ordóñez R. MPC for Optimized Energy Exchange between Two Renewable-Energy Prosumers. Applied Sciences. 2019; 9(18):3709. https://doi.org/10.3390/app9183709
Chicago/Turabian StyleAldaouab, Ibrahim, Malcolm Daniels, and Raúl Ordóñez. 2019. "MPC for Optimized Energy Exchange between Two Renewable-Energy Prosumers" Applied Sciences 9, no. 18: 3709. https://doi.org/10.3390/app9183709
APA StyleAldaouab, I., Daniels, M., & Ordóñez, R. (2019). MPC for Optimized Energy Exchange between Two Renewable-Energy Prosumers. Applied Sciences, 9(18), 3709. https://doi.org/10.3390/app9183709





