Supervised Machine Learning Techniques to the Prediction of Tunnel Boring Machine Penetration Rate

Abstract

Predicting the penetration rate is a complex and challenging task due to the interaction between the tunnel boring machine (TBM) and the rock mass. Many studies highlight the use of empirical and theoretical techniques in predicting TBM performance. However, reliable performance prediction of TBM is of crucial importance to mining and civil projects as it can minimize the risks associated with capital costs. This study presents new applications of supervised machine learning techniques, i.e., k-nearest neighbor (KNN), chi-squared automatic interaction detection (CHAID), support vector machine (SVM), classification and regression trees (CART) and neural network (NN) in predicting the penetration rate (PR) of a TBM. To achieve this aim, an experimental database was set up, based on field observations and laboratory tests for a tunneling project in Malaysia. In the database, uniaxial compressive strength, Brazilian tensile strength, rock quality designation, weathering zone, thrust force, and revolution per minute were utilized as inputs to predict PR of TBM. Then, KNN, CHAID, SVM, CART, and NN predictive models were developed to select the best one. A simple ranking technique, as well as some performance indices, were calculated for each developed model. According to the obtained results, KNN received the highest-ranking value among all five predictive models and was selected as the best predictive model of this study. It can be concluded that KNN is able to provide high-performance capacity in predicting TBM PR. KNN model identified uniaxial compressive strength (0.2) as the most important and revolution per minutes (0.14) as the least important factor for predicting the TBM penetration rate.

1. Introduction

The prediction of tunnel boring machine (TBM) performance in a specified rock mass condition is a longstanding research area. Suitable prediction of TBM performance parameters, notably the penetration rate (PR) and the advance rate (AR), can reduce the risks related to high capital costs, which are very common for mechanized excavation operations. This is an essential task for planning tunnel projects and selecting suitable construction methods. During the past decades, several empirical techniques have been developed for forecasting the performance parameters of TBM: PR, and AR [1,2,3,4,5,6,7]. In the aforementioned models/classifications, the most influential factors of rock mass and material, such as compressive and tensile strengths and joint conditions, as well as of machine specifications, such as average cutter force, and cutter-head torque, were utilized as predictors. A PR model was introduced by Farmer and Glossop [8] based on the tensile strength of the rock and average cutter force. In another study, conducted by Sanio [3], specific energy was predicted using values of uniaxial compressive strength (UCS) of the rock. Ozdemir [9] developed the Colorado School of Mines (CSM) model based on a database comprising of cutter and rock properties to estimate the cutter forces. The CSM model has since been modified several times by Rostami [5], Yagiz and Ozdemir [10], and Yagiz [11], by adding the effects of rock mass brittleness and rock mass fracture properties. Although these models have several inputs, most of these studies rely on rock properties, such as strength, joint spacing, and brittleness, as inputs into the established techniques [12,13,14,15,16].

Several studies used traditional statistical and linear techniques to predict TBM performance [17,18]. However, these techniques have been criticized, because of their disadvantages in solving highly complex and nonlinear problems. Grima et al. [19] mentioned that statistical models are not always robust enough to accurately describe nonlinear and complex systems. Moreover, their performance capacity is diminished in the presence of outliers and extreme values in the data. Furthermore, Farrokh et al. [20] stated that multiple parameters’ models use more project-specific data (compared to simple models), and are more easily applied (compared to computer-aided models). It should be mentioned that the performance capacities of the multiple parameters models are higher than those of simple parameter models. This is due to the use of more related input parameters. Hence, it seems that artificial intelligence (AI) and machine learning (ML) techniques can be the best choice to be applied for prediction of TBM performance using multiple input parameters.

AI and ML techniques (

Table 1. Published research on tunnel boring machine (TBM) performance prediction using related artificial intelligence (AI) and machine learning (ML) techniques.

Reference	Technique	Parameters		Datasets/Description
		Input	Output
Alvarez Grima [19]	ANN	CFF, Dc, RPM, TF, UCS	AR, PR	640 TBM projects
Bernardos and Kaliampakos [36]	ANN	N, overburden, permeability, RMR, rock mass weathering RQD, UCS, WTS,	AR	Athens metro tunnel
Yagiz [17]	ANN	BI, DPW, UCS, α	PR	151 datasets
Eftekhari et al. [39]	ANN	BTS, CT, Qu, RMR, Rock Type, RQD, Rs TF, UCS	PR	10 km data excavated in a tunnel
Gholamnejad and Tayarani [40]	ANN	DPW, RQD, UCS	PR	185 datasets
Gholami et al. [41]	ANN	Jc, Js, RQD, UCS	PR	121 tunnel sections
Salimi and Esmaeili [42]	ANN	BTS, DPW, PSI, UCS, α	PR	46 sections of a water supply tunnel
Torabi et al. [43]	ANN	C, UCS, υ, φ	PR, UI	39 sections of a highway project
Shao et al. [44]	ELM	BTS, DPW, PSI, UCS, α	PR	153 datasets
Mahdevari et al. [45]	SVR	BI, BTS, CP, CT, DPW, SE, TF, UCS, α	PR	150 datasets
Armaghani et al. [12]	PSO-ANN, ICA-ANN	BTS, UCS, RMR, RQD, TF, WZ, RPM	PR	1286 datasets
Armaghani et al. [37]	PSO-ANN, ICA-ANN	Qu, BTS, UCS, RMR, RQD, TF, WZ, RPM	AR	1286 datasets
Koopialipoor et al. [46]	FA-ANN	BTS, UCS, RMR, RQD, TF, WZ, RPM	PR	1200 datasets
Koopialipoor et al. [47]	DNN	BTS, UCS, RMR, RQD, TF, WZ, RPM	PR	1286 datasets

), such as artificial neural network (ANN), support vector machine (SVM), particle swarm optimization (PSO), and fuzzy inference system (FIS) have been widely used for solving problems in civil engineering and, more specifically, for TBM performance parameters [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]. ANN models were developed by Benardos and Kaliampakos [36] and Yagiz et al. [17] to predict TBM PR. Hybrid ANN models of PSO-ANN and imperialist competitive algorithm (ICA)-ANN were developed to approximate PR and AR of TBMs in the study conducted by Armaghani et al. [12] and [37], respectively. Recently, Koopialipoor et al. [13] developed a new model to predict the tunnel boring machine performance based on the group method of data handling. A gene expression programming (GEP) was introduced by Armaghani et al. [38] for estimating PR values obtained from a transfer tunnel in Malaysia.

While the use of AI techniques has attracted more attention than the use of other techniques, such as ML, in the field of tunneling the main aim of AI is the development of reliable and robust models. On the other hand, ML techniques seek to enhance accuracy, which is desirable for any prediction model. Since the TBM PR is a continuous target variable, the supervised ML techniques, such as SVM, nearest neighbor and decision trees (DTs) should be used for classification and regression of TBM data. Supervised ML approaches are powerful due to their ability to solve problems in science and engineering and obtaining a high accuracy level for prediction purposes, especially when dealing with highly complex and nonlinear problems [48,49,50].

This study aims to evaluate the use of various ML techniques in predicting the TBM PR. In this study, five ML techniques are developed to predict PR of TBM in hard rock conditions. The proposed models are compared in terms of accuracy and performance, to select the best models among them. This comparison helps decrease future work expended on choosing appropriate techniques/procedures for analysis of TBM and tunneling data. Thus, the importance of input variables to calculate the TBM PR is estimated and assessed using the selected models. This “importance” calculation can enable a better understanding of the predictive capacity of different input parameters.

It is extremely helpful to obtain prior knowledge of the TBM performance in rock excavation projects. This allows for planning construction time and for controlling cost, as well as choosing the excavation method. Several studies noted that predicting the penetration rate is a complex and difficult task because of the interaction between the TBM and rock mass. According to Jamshidi [51], TBM penetration rate directly influences the advance rate, which represents the total distance excavated by the machine divided by the total time. While there is a high cost associated with tunneling projects and using the TBM, utilizing prediction methods, especially ML techniques for predicting the penetration rate of TBM can significantly reduce the total time and cost of the tunneling projects. On the other hand, more investigations are needed in the field of TBM performance when there are different weathering zones in the rock-mass. As stated in several studies [6,52,53,54,55,56,57], the degree of rock-mass weathering has an enormous impact on rock mass properties as well as TBM performance. Hence, weathering index is used as an important input parameter in this study to predict TBM PR. In the following sections, the background of the applied ML models is described, and then, after developments of ML techniques, the best model among them will be selected for PR prediction.

2. Background of Supervised ML Models

2.1. K-Nearest Neighbor (KNN)

The k-nearest neighbor (KNN) is a non-parametric approach that was widely applied to statistics in the early 1970s [58,59]. According to Wu et al. [60], KNN is regarded as one of the top 10 algorithms in data mining, due to its simplicity, effectiveness, and implementation. The KNN-based classification technique can be effectively applied in several real-world and practical classification tasks in several fields, such as expert and intelligence systems. The KNN finds a group of k samples (e.g., using the distance functions) which are closest to unknown samples in the calibration dataset, constituting the basic theory of KNN. The KNN also determines the label (class) of unknown samples among the k samples through the calculation of the average of the response variables [61,62]. Consequently, k plays a significant role in the performance of the KNN [63].

2.2. Support Vector Machine (SVM)

Support vector machines (SVMs) is one of the most widely used algorithms for classification and regression problems [64]. This algorithm can effectively work with high dimensional and linearly non-separable datasets [48,65]. The basic theory behind the SVM is the statistical learning theory [66]. Kernel functions, such as linear, radial basis function, sigmoid and polynomial, also affect the SVM performance [67]. According to Hong et al. [65], the main aim of the SVM classifier is to identify an ideal separation hyperplane that can distinguish the two classes. The other advantages of SVM include a reduction in both the error (for training and testing datasets) and model complexity [68].

2.3. Neural Network (NN)

The basic structure of an ANN is the artificial neuron, that is, a mathematical model which resembles the behavior of the biological neuron, but with a plethora of activation functions enabling the biological neuron’s mainly sigmoid activation function [69]. To be precise, it should be noted that the scientists have decoded only a small amount of the biological neural networks (BNNs) structure, behavior, and functions. Therefore, to be exact, the similarity between biological and artificial neural networks is based mainly on morphological characteristics. Concerning the practical terms, NNs are non-linear statistical data modeling techniques or tools of decision making. The NN can find patterns in data, or unveil relations between inputs (dependent parameters) and output (independent parameter). NNs can be applied to different fields, such as function approximation, classification, and data processing. In NNs, the weights denote the connections of the biological neuron. An excitatory connection is reflected by a positive weight, while an inhibitory connection is reflected by a negative value.

2.4. Classification and Regression Trees (CART)

Classification and regression trees (CART) is a binary DT which was developed by Breiman et al. [70]. This modeling approach aims to find the best possible split. For various types of variables, the CART categorize values of the input variables from smallest to largest values. To identify the best split point, the technique makes a trial split. For instance, if the call split point is called “S”, then all the cases with value below “S” go to the left, forming the child node (X < S). Otherwise, instances are sent to the right child node (X > S). The CART seeks to reduce the impurity of the leaf nodes to choose the best data partition. Three potential indices are considered in CART technique for selecting the best data partition: Gini criterion entropy, and Twoing criterion. The CART performance is affected by the selection of these indices. The best prediction performance can be obtained when the perfect selection of indices has been accomplished.

2.5. Chi-Squared Automatic Interaction Detection (CHAID)

Chi-squared automatic interaction detection (CHAID) is a data mining algorithm and DT which was developed by Kass [71]. This algorithm grew a DT by several sequential combinations and splits, based on Chi-square test. The CHAID is a tree-based structure technique, which is a combination of a group rule classifiers. This technique creates a tree structure of the dependent parameters to predict the independent parameter. The ratio of records having the specific value for the target variable to the given values for the independent variables denotes the confidence (accuracy) of the created rules. The CHAID attempts to produce wider and non-binary trees. Besides, it automatically prunes the DT to avoid overfitting.

3. Materials and Methods

The present study uses a ranking system to identify the most accurate model to predict PR. The models that are used in this study are KNN, SVM, NN, CART, and CHAID. These supervised techniques were selected because of their effectiveness to predict the continuous target variables, as well as on account of their wide applicability. The parameters that were used to develop the abovementioned models are presented in

Table 2. Parameters of the algorithms used in this study.

KNN	SVM
Number of nearest neighbors (k): Minimum 3 and maximum 5 Distance computation: Euclidean metric Prediction for range target: Mean of nearest neighbor values Stopping criteria: Stop when the 10 features have been selected	Stopping criteria: 1.E-3 Regularization parameter (C): 10 Regression precision (epsilon): 0.1 Kernel type: RBF RBF gamma: 0.1
NN	CHAID
NN model: Multilayer perceptron (MLP) Stopping rules: Use maximum training time (per component model): 15 minutes Combining rule for continuous targets: Mean Number of component models for boosting and/or bagging: 10 Overfit prevention set (%): 30 Missing values in predictors: Delete listwise	Tree growing algorithm: CHAID Maximum tree depth: 5 Minimum records in parent branch (%): 2 Minimum records in child branch (%): 1 Combining rule for continuous targets: Mean Number of component models for boosting and/or bagging: 10 Significance level for splitting: 0.05 Significance level for merging: 0.05 Adjust significance values using Boferroni method Minimum change in expected cell frequencies: 0.001 Maximum iterations for convergence: 100
CART
Maximum tree depth: 5 Prune tree to avoid overfitting: maximum surrogates: 5 Minimum records in parent branch (%): 2 Minimum records in child branch (%): 1 Combining rule for continuous targets: mean Number of component models for boosting and/or bagging: 10 Minimum change in impurity: 0.0001 Over-fit prevention set (%): 30

. To develop the models, the authors used IBM SPSS modeler 18. The details of the methods implemented to assess the selected techniques and dataset preparation are presented in the following sub-sections.

3.1. Model’s Assessment

In this study, four performance indices, namely coefficient of determination (R²), mean absolute error (MAE), root mean square error (RMSE), and variance account for (VAF), were used to measure the prediction performance and accuracy of the developed models. These indices are widely used to assess the accuracy of the developed models in the related studies as well [72,73,74,75,76,77,78,79]. Furthermore, the recently proposed a²⁰-index have been used for the evaluation of models. These indices are computed as follows:

$$VAF=\left[1-\frac{var\left(y-y^{\prime }\right)}{var\left(y\right)}\right]\times 100$$

(1)

$$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left(y-y^{\prime }\right)}^2}$$

(2)

$$R^2=1-\frac{{{\displaystyle \sum }}_i{\left(y_i-f_i\right)}^2}{{{\displaystyle \sum }}_i{\left(y_i-\overline{y}\right)}^2}$$

(3)

$$MAE=\frac{1}{N}{\displaystyle \sum }_{j=1}^N\left|y_i-y_j\right|$$

(4)

where y denotes the measured values, ȳ and y′ indicate mean and predicted the values of y, respectively, N denotes the total number of data. Note that, a predictive model with R² of 1, VAF of 100%, and RMSE and MAE of zero is defined as a perfect model. The dataset should be divided into two phases (i.e., training and testing) to develop the model and then evaluate the developed model. Thus, in this study, according to suggestions of several studies [21,80,81,82], 80% of the collected data (or 167 datasets) are randomly selected to train the models and the remaining 20% of the data (or 42 datasets) are used to test and validate the models. The simple ranking technique proposed by Zorlu et al. [83] was used in this research. According to this technique, the total rate of each model is calculated for training and testing dataset, separately. The highest rate value for each performance index is five because we have five models, and the best performance index is assigned the highest rating (5). The total performance rating of each model is then calculated by summing up its total rank of training and total rank of the testing dataset. More information regarding the simple ranking technique can be found in the original study, Zorlu et al. [83].

Furthermore, the following, recently proposed engineering index, the a²⁰-index, is proposed for the reliability assessment of the developed AI models:

$$a^{20}-index=\frac{m^{20}}{M}$$

(5)

where M is the number of dataset samples and m²⁰ is the number of samples with a value of rate experimental value/predicted value between 0.80 and 1.20. Note that for a perfect predictive model, the values of a²⁰-index values are expected to be unity. The proposed a²⁰-index has the advantage that their value has a physical engineering meaning. It declares the amount of the samples that satisfies predicted values with a deviation of ± 20% compared to experimental values.

3.2. Case Study and Data Preparation

A tunnel project (PSRWT, Pahang–Selangor raw water transfer) with a total length of 44.6 km and a diameter of 5.23 m was planned and constructed in Malaysia. This tunnel aims to transfer water from Pahang state to Selangor state. PSRWT tunnel was excavated in a mountain area of Peninsular Malaysia, where six major faults were observed with an elevation range from 100 to 1200 m. In the field, rock strength is poor in areas of fault intersections and highly to moderately weathered zones were observed along the tunnel. Different rock types including shale, coarse-grained granite, and medium-grained granite were observed in various tunnel distances (TDs) of PSRWT tunnel. Regarding construction techniques for the tunnel excavation, there were seven parts, comprising four parts of NATM and three parts of TBM. In PSRWT tunnel project, 11,761 m in the mixed ground, 11,761 m in very hard ground and 11,218 m in the blocky ground were excavated by three TBMs. Construction`s of PSRWT tunnel with their maximum overburden are shown in Figure 1.

There is a need to have a suitable database with the most effective parameters of TBM performance for prediction of TBM PR. The most effective parameters on TBM performance can be identified by reviewing the previous related studies. Based on the literature, three groups of parameters are found as the most effective factors of TBM performance, including machine characteristics, rock mass, and rock material properties [84]. According to Benardos and Kaliampakos [36], the most important parameters affecting the TBM performance are rock quality designation (RQD), UCS, rock-mass weathering, and rock mass rating (RMR). As some researchers (e.g., [52,53]) have concluded and pointed out, the rock mass weathering can significantly affect the TBM PR. Sapigni et al. [85] found that UCS and RMR can significantly affect the TBM performance. They also noticed that the Brazilian tensile strength (BTS) could be set as an input parameter. Grima et al. [19] found an inverse relationship between PR and UCS. Farrokh et al. [20] showed in their research that factors such as RQD, the diameter of tunnel, UCS, type of rock, disc-cutter normal force, and revolution per minute (RPM) were of the highest influence on PR. Whereas, Mahdevari et al. [45] introduced a different list in this term, including UCS, BTS, intact rock brittleness (BI), cutter head power (CP), cutter-head torque (CT), the distance between the plane of weakness (DPW), and thrust force (TF).

An investigation of about 13 km was conducted in the PSRWT tunnel and a database with 209 datasets was prepared. Rock type in the investigated areas was granite covering three weathering zones, i.e., fresh, slightly weathered, and moderately weathered. According to International Society of Rock Mechanics (ISRM) [86], a typical rock weathering profile is composed of six weathering grades namely fresh, slightly weathered, moderately weathered, highly weathered, completely weathered, and residual soil. This classification is mainly based on discoloration and decomposition of the rock material. Based on tunnel mapping 34,740 m of PSRWT tunnel which was excavated by TBMs, a total of 12,649 m comprising 5443 m in fresh, 5530 m in slightly weathered, and 1676 m in moderately weathered zones, was observed. In this study, in terms of rock mass properties, many points in three TBMs were investigated and several rock mass properties, such as type of rock, strength, degree of weathering, joint condition (e.g., spacing of discontinuities, alteration, degree of roughness, infilling material), and groundwater condition, were quantified and database established. Furthermore, machine characteristics, such as TF, RPM, PR, AR, boring energy, stroke speed, and cutterhead torque, were recorded by TBMs. For rock material evaluation, more than 100 block samples were collected from the face of PSRWT tunnel project and after transferring to the laboratory, several tests, e.g., density, BTS, point load strength, Schmidt hammer, p-wave velocity, and UCS were carried out based on ISRM [86]. According to several authors [54,55,87,88,89,90,91,92], the most known geomechanical tests used to establish the quality state of the rock masses are RQD, Schmidt hammer, UCS, p-wave velocity, etc. A failed sample under Brazilian test conducted in the laboratory is shown in Figure 2. Besides, a conducted UCS test on a sample before and after failure is shown in Figure 3.

In this study, based on the literature review, available field observations, and laboratory tests, six parameters, UCS, BTS, RQD, WZ, TF, and RPM, were selected as model inputs to estimate TBM PR. It is important to mention that RQD was calculated based on the method suggested by Bieniawski [93]. Note that value was assigned to each WZ in the used datasets, i.e., 1, 2, and 3 were assigned to fresh, slightly weathered, and moderately weathered, respectively.

Table 3. Descriptive statistics of the experimental database used in this research.

Parameter	Type	Symbol	Unit	Min	Max	Average	St Dev
Rock quality designation	Input	RQD	%	10	95	53.5	27.7
Uniaxial compressive strength		UCS	MPa	49	185	122.7	40.7
Weathering zone		WZ	-	1	3	1.8	0.8
Brazilian tensile strength		BTS	MPa	4.69	15.1	9.6	3.2
Thrust force per cutter		TF	kN	83	513.5	276.8	133.1
Revolution per minute		RPM	rev/min	4.5	11.9	8.6	2.4
Penetration rate	Output	PR	m/h	1.11	3.75	2.4	0.6

presents a basic statistical description of the experimental database applied in the current research. For more information regarding the data used in this study, the correlation matrix of input and output variables for all 209 cases is shown in Figure 4. High negative or positive values of the correlation coefficient between the input variables may result in poor efficiency of the methods and a difficulty in construing the effects of the expository variables on the response. As can be seen in Figure 4, there are no significant correlations between the independent input variables. Additionally, a detailed flowchart of this study for the prediction of TBM PR is presented in Figure 5. According to this flowchart, after literature review and site selection, data collection is divided into two sections of laboratory tests and field observation. Therefore, all influential parameters on TBM performance are recorded and considered as model inputs. To predict TBM PR, SVM, KNN, CHAID, NN, and CART are applied and developed. Then, an evaluation will be performed for each model and the best one among them will be selected and introduced as the best predictive model. In the following sections, the modeling process of ML techniques for the PR estimation and their evaluations based on performance indices will be explained.

4. Results and Discussion

4.1. Assessment of Models

In this study, KNN, SVM, NN, CART, and CHAID models were applied for PR prediction. Each of them has been conducted several times based on their most effective parameters. To evaluate the prediction performance of the mentioned techniques, the established TBM dataset was split into two sections of training and testing. Therefore, 209 cases of the data were separated into 167 and 42 as train and test sections and then the model constructions were conducted to forecast the TBM PR.

The values of the performance indices for the proposed KNN, SVM, NN, CART, and CHAID models were calculated and are presented in

Table 4. The obtained results of performance indices for all predictive models in estimating TBM PR.

Method	Stage	R2	RMSE	VAF	MAE	a20-Index	R2 Rank	RMSE Rank	VAF Rank	MAE Rank	a20-Index Rank	Total Rate
NN	TS	0.924	0.180	91.735	0.137	0.944	5	5	5	5	4	24
	TR	0.916	0.173	91.602	0.136	0.967	1	2	1	1	2	7
SVM	TS	0.914	0.183	91.393	0.139	0.981	4	4	4	4	5	21
	TR	0.942	0.144	94.207	0.114	0.987	3	4	3	2	4	16
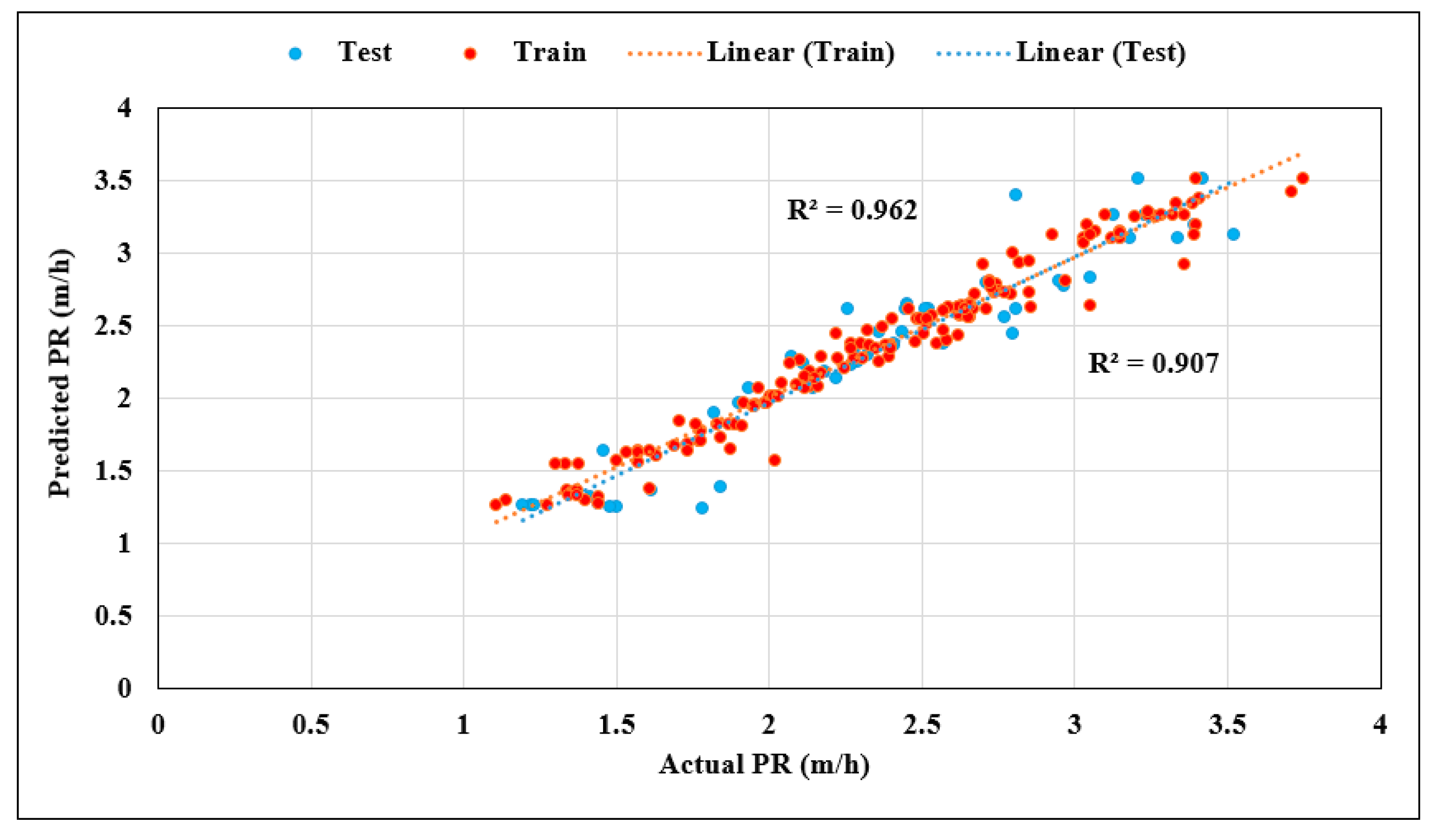
KNN	TS	0.907	0.204	89.574	0.157	0.944	3	3	3	3	4	16
	TR	0.962	0.116	96.226	0.081	0.993	5	5	5	5	5	25
CART	TS	0.897	0.216	88.020	0.164	0.944	2	2	2	2	4	12
	TR	0.944	0.144	94.265	0.104	0.993	4	4	4	4	5	21
CHAID	TS	0.850	0.252	83.838	0.179	0.944	1	1	1	1	4	8
	TR	0.934	0.153	93.389	0.110	0.980	2	3	2	3	3	13

TR: Training, TS: Testing.

. These results are based on testing and training datasets and using the simple ranking technique (as described earlier). Table 4 shows that the KNN model has the highest total rate (25) among the models of the training dataset. For the testing dataset, the NN model has the highest total rate, amounting to a value of 24. The total performance ratings of the models for both training and testing datasets are also indicated in

Table 5. Total performance ratings.

	NN	SVM	KNN	CART	CHAID
Grand total rank	31	37	41	33	21

. According to this table, the KNN model obtained the highest total performance rating, which is 41 (25 for training and 16 for testing). The following sub-section provides a more detailed analysis of the KNN model for PR prediction.

4.2. Result of Selected Models

As mentioned in the previous section, KNN has been selected as the best predictive model of TBM PR. Figure 6 and Figure 7 show the suggested structure of the KNN predictive model in predicting PR of TBM. In the development of the k-NN model, the objective of performing the model was to establish the balance between speed and accuracy. Therefore, the model automatically selected the best number of neighbors, within a small range. In the present study, we used k number between the values 3–5 by implementing a trial-and-error method of the system. Figure 6 presents the predictor space chart of the KNN model. In this figure, the predictor space gave excellent results, using the three input variables of UCS, RQD, and BTS as predictors for predicting the PR. The predictor space chart is an interactive graph of the predictor space and is directly printed out from the software. Any dot can temporarily become a focal record if selected. “Focal records” are simply points selected in the predictor space chart. If a focal record variable is specified, the points representing the focal records will initially be selected and becomes red. Figure 7 shows the relationship between the predictors and K selection. In the horizontal axis of the chart, the numbers of the nearest neighbor are presented. Sums of square errors are shown in the vertical axis. As shown by the figure, the errors for k = 3, 4, and 5 were determined as 7.41, 7.39, and 7.85, respectively. The results reveal that k = 4 is the best value of the nearest neighbor numbers for the developed k-NN model.

Predicted PR values by KNN, along with their actual values for training and testing datasets, are displayed in Figure 8. The R² between predicted and actual PR in training and testing dataset were 0.962 and 0.907, respectively. Besides, an RMSE of (0.204 and 0.116), a VAF of (89.574% and 96.226%) and an MAE of (0.157 and 0.081) were obtained for testing and training datasets of the best predictive model of this study, respectively. These results show that KNN, as a newly developed model in the field of TBM performance, can provide higher prediction performance compared to other predictive models. It is worth mentioning that CHAID (as a tree-based model) was also implemented for the first time in this field with the obtained R² values of 0.850 and 0.934, for testing and training datasets, respectively, which showed an enhanced performance of this model in solving TBM performance. Compared to other published studies related to the same tunnel [12,13,38], this study has a different database with a slightly higher prediction performance. For example, in terms of R², values of (0.897 and 0.905) and (0.919 and 0.912) were obtained by PSO-ANN and ICA-ANN techniques, respectively in the study conducted by Armaghani et al. [12]. In another study, Koopialipoor et al. [13] developed the group method of data handling technique to solve TBM PR. They obtained R² results of 0.946 and 0.924 for training and testing datasets, respectively. A GEP model was developed by Armaghani et al. [38] to predict TBM PR, with R² values of 0.855 and 0.829 for training and testing datasets, respectively. Based on the above discussion, the developed KNN model in this study can provide higher prediction capacity compared to previously published studies.

In order to understand the influence of each input parameter on PR results, sensitivity analysis has been performed through the developed KNN model. To do this, the importance or weight of each input parameter on system output can be obtained. The importance of the input parameters analyzed by the KNN technique is shown in

Table 6. Importance of input variables in the developed KNN model.

Input Variable	Importance
RPM	0.14
WZ	0.15
BTS	0.16
RQD	0.17
TF	0.18
UCS	0.20

. As shown in this table, KNN identified USC as the most important input variable for predicting the PR, while RPM was considered as the least important input variable for predicting the PR. These results are in good agreement with previous investigations in the field of tunneling and underground space technologies [19,94,95]. The results of sensitivity analysis can be used by other researchers in further investigations to select the most influential parameters on TBM performance.

5. Conclusions

The present study evaluated the relative importance (weight) of different input variables influencing PR. Initially, different supervised ML approaches were compared aiming to identify the most accurate modeling approach. Five supervised ML techniques were selected and evaluated, i.e., KNN, SVM, NN, CART, and CHAID. These modeling approaches were selected because of their ability to handle continuous target variables. A variety of ML techniques were conducted to predict TBM PR using a database comprising of 209 datasets including the most important parameters on TBM PR. Performance of the five mentioned ML techniques was evaluated using a simple ranking technique and some performance indices, i.e., R², RMSE, VAF, and MAE. According to the obtained results, the KNN predictive model was identified as the optimum model. A total ranking value of 32 was obtained by the KNN model, while other techniques obtained ranking values of 25 (NN), 28 (SVM), 24 (CART), and 14 (CHAID). R², RMSE, VAF, and MAE values of (0.907, 0.204, 89.574, and 0.157) and (0.962, 0.116, 96.226, and 0.081) were recorded for the developed KNN, as the selected predictive model of this study. Besides, the results of KNN are enhanced concerning the previously published results in the field of TBM performance prediction. It can be concluded that the KNN predictive model should be applied in similar conditions to examine the capability of this technique in the field of geotechnical engineering. Furthermore, “importance” (weight) results of the various input variables show that USC and RPM are the most and the least important input variables, respectively, when applying the KNN model.