1. Introduction
In the early years of baseball, bats were made from a wide variety of wood species as players explored various woods in their quest to find the perfect wood. Eventually, northern white ash became the wood of choice as it had the best combination of density, stiffness, and impact resistance properties. For example, hickory has better impact resistance than the northern white ash, but it is denser than ash, thereby making for a relatively heavy bat. In the late 19th century, the Hillerich family in Louisville, Kentucky cemented the central role of ash bats in baseball when it began manufacturing northern white ash bats for a number of professional teams [
1].
Ash remained the wood of choice until the late 1990s when maple bats were introduced to players by Sam Bat, and a small number of players transitioned from ash to maple [
2]. As the popularity of maple bats increased, the rate at which bats were breaking into multiple pieces during games was perceived to be increasing as well. However, there were no data to support whether this phenomenon was real or perceived. To obtain concrete data on the phenomenon, Major League Baseball (MLB) in cooperation with the Major League Baseball Players Association (MLBPA) authorized the collection of all bats that broke in games during a 2½-month portion of the 2008 MLB regular-season. Visual inspection of these broken bats concluded that the slope-of-grain (SoG) of the wood in each of the bats played a major role in the likelihood of a bat breaking into multiple fragments [
3]. Slope-of-grain is defined to be the angle of the grain of the wood in the bat with respect to a line parallel to the longitudinal axis of the bat.
As a result of the SoG observations from the field-collection bats and the understanding of the mechanical behavior of maple from a wood-science perspective, the wood-science experts on the team recommended new regulations be implemented after the 2008 season with respect to (1) setting the allowable range of SoG to be ±3° and (2) changing the hitting surface for maple bats from edge grain to face grain. Before limiting the allowable range of SoG to be ±3°, many bat manufacturers were not closely monitoring SoG, and therefore, allowing wood with SoGs of up to ±10° to be used in bats.
After the 2009 season, additional regulations were implemented to restrict the minimum allowable wood density to 0.0245 lb/in
3 (678 Kg/m
3) for maple wood species that could be used to manufacture baseball bats. Before this limitation was implemented, any species of maple was allowed to be used to make a wood bat. Without a list of specific maple species, maple species with poor impact properties were sometimes being used. After the introduction of the strict limitation to a single species of maple and greater awareness and compliance with the new regulations, the MPF rate dropped an additional 15–20% between the 2009 and 2010 seasons [
4]. Each of the new regulations had the benefit that the improvements in bat durability came with changes that were fairly transparent to the players, i.e., there were no bat geometries or popular wood species that were prohibited from use.
The combination of (1) setting the allowable range for SoG to be ±3°, (2) changing the impact surface from the edge to face grain for maple, and (3) the restriction on the minimum allowable wood density of 0.0245 lb/in
3 (678 kg/m
3) for the wood species of maple resulted in a measurable decrease of ~65% in the MPF rate per game [
5]. Of these three changes, the only one that has an option to offer any additional drop in the MPF rate without any increase in bat weight is a further tightening of the allowable SoG from ±3°. To explore if and how a further tightening of the allowable SoG could improve upon the MPF rate, the durability of sets of bats sorted by SoG, e.g., sorted into four SoG groupings, specifically (1) |SoG| ≤ 1°, (2) 1° < |SoG| ≤ 2°, (3) 2° < |SoG| ≤ 3°, and (4) |SoG| > 3°, could be tested in the lab. However, such an approach would be difficult due to the inherent variability of wood and the lack of control over the factors unrelated to SoG, such as density or the ultimate strength of the wood, thereby making it challenging to draw conclusive trends. In addition, it would also be expensive with respect to the large number of bats that would need to be explored for such a study, as well as the time required to characterize the durability of all bats in the study and subsequent examination of all bat failures. An alternative and cost-effective approach is to use the finite element method to investigate how the failure mode changes as a function of SoG for a range of representative on-field relative bat/ball speeds and impact locations [
6,
7,
8].
In the current paper, a popular bat profile is used in a parametric study to investigate the relationship between SoG and bat durability. During a game, the relative bat/ball impact velocity can range from 90–180 mph (145–290 kph) and is a consequence of the combination of the pitch speed, swing speed, and impact location along the length of the bat. For the purposes of this paper, bat durability is defined as the relative bat/ball speed that results in bat breakage, i.e., the higher the speed required to initiate bat cracking, the better the durability. The finite element models of this bat profile are analyzed using LS-DYNA where the variables in the parametric study include (1) SoG—ranging between ±10°, (2) Wood species—Ash, Maple, and Yellow Birch, (3) two impact locations—2.0 in. (5.1 cm) and 14.0 in. (35.6 cm) as measured from the tip of the barrel, and (4) relative bat/ball impact speeds between 90 and 180 mph (145–290 kph). This paper presents the first comprehensive numerical investigation into the relationship between SoG and bat durability. Prior to this numerical study, limited empirical data from bats broken during games and in-laboratory studies where SoG was not a controlled variable were available to imply a qualitative relationship between SoG and bat durability. The results of this study can serve as the basis for developing future parametric studies using finite element modeling to explore a large set of bat profiles and thereby to develop a deep fundamental understanding of the relationship among bat profile, wood species, wood SoG, wood density, and on-field durability.
2. Background
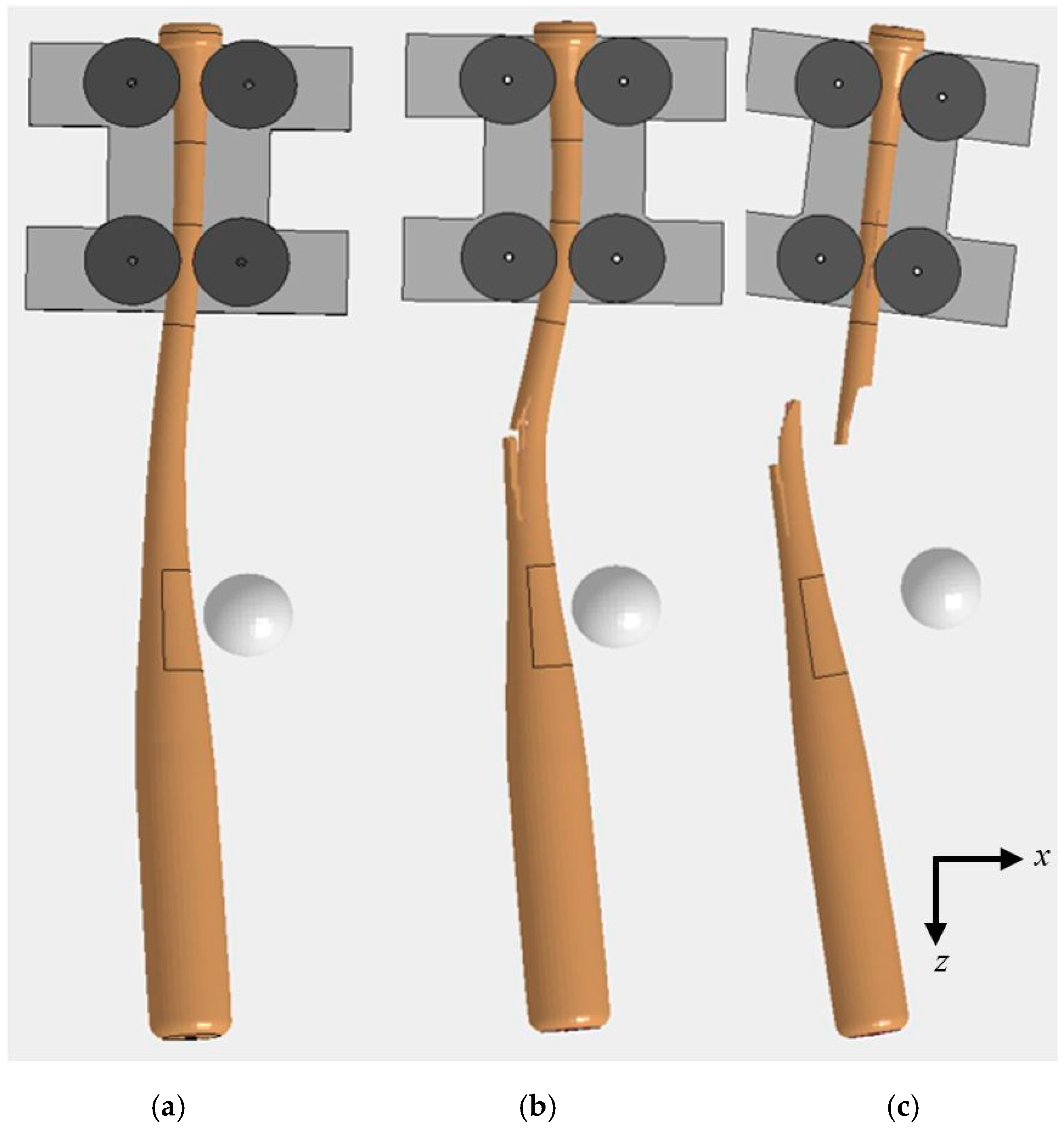
Baseball bats are comprised of four major regions, as shown in
Figure 1. The barrel is the intended ball impact region. The barrel of a typical 34.0 in. (86.4 cm) long baseball bat extends from the tip of the barrel to 10.0–12.0 in. (25.4–30.5 cm) down the length of the bat. The taper region is where the diameter of the bat transitions from the large diameter of the barrel to the small diameter of the handle. The taper region of a 34.0-in. (86.4 cm) bat runs from the end of the barrel section to about 20.0 in. (50.8 cm) from the tip of the barrel. Manufacturers are required to place their company label on this region of the bat, and the location of the label should be located 90° away from the intended hitting surface of the bat such that a batter can follow the protocol of hitting with the label up or label down. The handle of a baseball bat is the section that a player grips when swinging. The handle of a 34.0 in. (86.4 cm) bat extends from the end of the taper region to about 33 in. (84 cm) from the tip of the barrel. The final ~1 in. (~2.5 cm) of a wood baseball bat is the knob, which has a diameter a bit larger than that of the grip area so as to help the player maintain his hold on the bat during the swing.
Upon the wide acceptance of northern white ash as the wood of choice, the players also settled on holding the bat such that the ball would impact the edge grain of the wood as opposed to the face grain (
Figure 2). As a result, bat manufacturers located their logo on the face grain of the bat, i.e., 90° away from the edge grain. Thus, players would commonly hit with the logo up or logo down.
Figure 1 shows an example of the location of the Louisville Slugger logo on the face-grain surface of an ash bat.
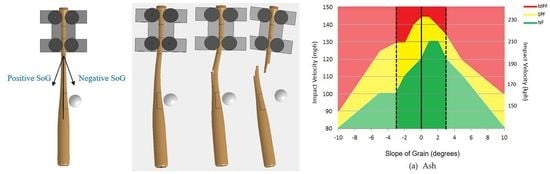
Figure 3 shows the respective directions of positive and negative SoGs for a label-up orientation of the bat and the ball traveling from the pitcher to home plate. In
Figure 3, the bat is shown situated in a finite element model of the bat durability testing system at the University of Massachusetts Lowell Baseball Research Center (UMLBRC).
An SoG of 0°, i.e., the grain of the wood is aligned with the long axis of the bat, is alleged to be the optimal condition for bat durability. As the SoG deviates from 0°, the effective break strength, i.e., the modulus of rupture, of the wood decreases [
6,
9,
10,
11]. Hankinson’s equation can be used to quantify the effect of SoG on wood mechanical properties,
where
N is the strength at an angle θ to the fiber direction, P is the strength perpendicular to the fiber, Q is the strength parallel to the fiber, and n is an empirically determined constant [
10]. Different properties follow different curves (
Figure 4), and these curves are average relationships developed across many species. The Wood Handbook states that the modulus of rupture (MOR) falls very close to the curve Q/P = 0.1 and n = 1.5. Using these values, the Hankinson Equation for a 3° SoG results in
N = 0.895, meaning that the strength of a 3° SoG specimen is 89.5% of a specimen with a 0° SoG.
The MOR curve in
Figure 4 shows that an SoG of ±10° will result in a 60% drop in MOR—thus, the motivation to tighten the allowable SoG range to be ±3°. The motivation for the change in hitting surface was based on the knowledge that the impact resistance of maple, a diffuse porous wood, is better on the face grain than on the edge grain. This behavior is opposite to the impact durability of northern white ash, a ring porous wood species, which demonstrates superior durability when impacted on the edge grain face [
12]. Recent Charpy testing of wood corroborated these differences in the hitting surfaces for ash and maple [
6]. The tighter tolerance on the allowable SoG and the change in the hitting surface for maple from the edge to face grain for the 2009 season contributed to the rate of MPFs decreasing by 30% from what was observed in 2008 [
13].
4. Results
The results of the finite element simulations for a range of wood SoGs were analyzed to investigate the mode of failure and durability as a function of the combination of SoG, impact velocity, wood species, and impact location. For each of the three wood species, 275 simulations were run, i.e., 176 simulations for 2.0 in. (5.1 cm) impact and 99 simulations for 14.0 in. (35.6 cm) impact. In total, 825 bat/ball impact simulations were run for this study.
Contour plots depicting the three outcomes as a function of SoG and impact speed were developed for each combination of wood species and impact location, and the contour plots of the 14.0 in. (35.6 cm) and 2.0 in. (5.1 cm) models are presented in
Figure 10 and
Figure 11, respectively. The impact-velocity range for each of the possible outcomes of the bats is denoted by color– see the legend in plots. The vertical dark black line in each of these plots denotes the 0° SoG, and the two-vertical dashed black lines bound the range of compliant SoGs as defined by MLB standards for use in baseball bats, i.e., ±3°. In
Figure 12 and
Figure 13, the results of the three wood species are overlaid for each of the different outcomes. These figures show a direct comparison of the speeds and SoG associated with the respective boundaries between NF to SPF and with the respective boundaries between SPF to MPF.
5. Discussion
Figure 10 and
Figure 11 are contour plots to show how the response of the bat transitions to each of the three outcomes as a function of impact velocity and SoG for impacts at the 2.0 in. (5.1 cm) and 14.0 in. (35.6 cm) locations, respectively. There is one contour plot for each combination of wood species and impact location that was considered in the parametric study. The NF regions are denoted in green, the SPF regions in yellow, and the MPF regions in red.
Figure 10 shows that the maximum speed for the NF region for all three wood species when impacted at the 2.0 in. (5.1 cm) location is in the range of SoGs progressing from 0° to −1°, and the breaking speed drops for SOGs on either side of this 1° spread. These results of the outside-pitch 2.0 in. (5.1 cm) impact models imply that the negative-SoG wood for values between 0° and −1° can withstand higher impact velocities before failure than the 0°-SoG wood. The relatively narrow bands of SPF for the maple and ash in comparison to the height of the SPF band for yellow birch imply that ash and maple bats quickly transition from SPF to MPF with less increase in speed than for yellow birch bats. It can also be concluded from the contour areas shown in
Figure 10 that using wood with an SoG outside of the range of ±3° for any one of the wood species results in a sharp decrease in bat durability. Thus, the 2.0 in. (5.1 cm) modeling provides virtual scientific data to support the 2008 recommendation that the SoG range be set to ±3°.
Figure 11 shows that the maximum speed for the NF region for all three wood species is in the range of SoGs progressing from +1° to +2°. The maximum NF speed then trails off as the SoG increases to +3° and higher and as the SoG goes from +1° and lower. These results of the 14.0 in. (35.6 cm) inside-pitch impact models show that the positive-SoG wood for values between 0° and 3° can withstand higher impact velocities before transitioning to an SPF than the negative-SoG wood. It can also be concluded from the data shown in
Figure 11 (as it was from
Figure 10) that using wood with a SoG outside of the range of ±3° for any one of the wood species results in a sharp decrease in bat durability, which also supports the recommendation that the SoG range be set to ±3°.
Figure 12 is an overlay plot of the boundaries denoting the transition from NF to SPF (solid lines) and for the transition from SPF to MPF (dashed lines), respectively, for all three wood species when impacted at the 2.0-in. (5.1-cm) location.
Figure 12 shows that the yellow birch bats transition from NF to SPF at lower velocities for the entire range of ±10° SoGs in comparison to the maple bats and for most of the range of ±10° SoGs relative to the ash bats. However,
Figure 12 also shows that the yellow birch bats had a much higher durability for the transition from SPF to MPF than maple and slightly better than ash. Thus, maple is the most likely of the three wood species to result in an MPF at the high end of the bat/ball impact speeds when viewing the results in the SoG range of ±3°, and this probability of maple breaking in an MPF manner relative to ash and yellow birch increases for SoGs outside the ±2° range. Thus, the modeling implies that the rate of maple bat MPFs due to inside pitches could be measurably reduced if the SoG range for maple were decreased from ±3° to ±2°.
Figure 13 is an overlay plot of the boundaries denoting the transition from NF to SPF (solid lines) and for the transition from SPF to MPF (dashed lines), respectively, for all three wood species when impacted at the 14.0 in. (35.6 cm) location. The yellow birch bats transition from NF to SPF at much lower velocities in comparison to the maple bats and slightly lower than the ash bats. For example, the transition velocities from NF to SPF for a bat with a −3° SoG for maple and ash are 115 and 110 mph, respectively, while the yellow birch is 100 mph. However, the yellow birch bats once again had a much better durability window (for both velocity and SoG span) in their transition from SPF to MPF than the other two species. This 14.0-in. (35.6‑cm) modeling implies that the rate of MPFs due to outside pitches could be reduced if the SoG range for all three kinds of wood were decreased from ±3° to ±2°.
There are several general observations that can be made from the analysis of the models. Negative-SoG bats in the range of 0° to −1° exhibit a higher SPF durability than positive-SoG bats for all three wood species for a 2.0 in. (5.1 cm) impact. As the impact speed increases to the MPF boundary, the best durability is at a 0° SoG. Positive-SoG bats in the range of +1° to +2° exhibit a higher SPF durability than negative-SoG bats for all three wood species for a 14.0 in. (35.6 cm) impact. This phenomenon continues for yellow birch bats as they transition from an SPF to an MPF. As the impact speed increases to the MPF boundary, the best durability is at a 0° SoG for ash and maple bats. The bias of the peak durabilities to be for negative-SoGs for outside-pitch (2.0 in., 5.1 cm) impacts and to be for positive SoGs for the inside-pitch (14.0 in. 35.6 cm) impacts supports that a 0°-SoG bat is the most versatile with respect to bat durability.
Based on the Hankinson equations as plotted in
Figure 4, it was expected that bat durability would decrease as the magnitude of SoG increases. Thus, it is unexpected to see the results of increased bat durability for small nonzero SoGs, i.e., increase in bat durability for small negative SoGs for the 2.0 in. (5.1 cm) outside-pitch impact and the increase in bat durability for small positive SoGs for the 14.0 in (35.6 cm) inside-pitch impact. The respective increases with opposite SoGs may be a consequence of the respective deformation mode and location of the maximum strain for each of the two impact conditions. For the outside-pitch condition, the bat exhibits a diving board mode shape, i.e., like that of a beam clamped at one end with a backward tip deflection—see
Figure 8a. For the inside-pitch condition, the bat bends in the reverse direction of that described for the outside-pitch situation with the zero-slope near the middle of the length of the bat—see
Figure 8b. Thus, for the outside pitch, the front side of the bat is in tension with the maximum strain in the handle section near the knob. For the inside pitch, the back side of the bat is in tension with the maximum strain developing in the taper section of the bat. This bat response was visually confirmed during high-speed video recordings of impacts and could be validated experimentally through digital image correlation (DIC) or by placing strain gauges along the length of the bat. The difference in the sensitivity of the range of SoG may be a consequence of the respective bat section that is experiencing the maximum strain for the respective impact location. With respect to how the material behavior contributes to this increase in bat durability for small non-zero SoGs, a plausible explanation may be at what magnitude of bending do the wood fibers become fully engaged in the deformation process. Future studies will look at extreme changes in bat profiles to see if the trends found for this bat profile are also seen in those other profiles. Simple parametric studies of beam bending for the range of SoGs used in this parametric study may give insight into the specifics of the mechanical behavior of the material that may explain the results.
There are several minor limitations with the model used in this paper. The SoG is modeled as the same throughout the length of the bat. In reality, there will be some variation of the SoG along the length of the bat. However, this limitation is minor because the SoG in the handle dominates over the SoG elsewhere on the bat. There are only a few lab experimental results to use for comparison to the model. The wood properties are taken as nominal.