Application of an Adaptive “Neuro-Fuzzy” Inference System in Modeling Cutting Temperature during Hard Turning

Featured Application

Development of an adaptive neuro-fuzzy inference systems (ANFIS) for the recognition and prediction of the cutting temperature in hard turning that can meet industrial requirements.

Abstract

The machining of hard materials with the most economical process is a challenge that is the aim of production systems. Increasing demands of the market require a hard processing hardened steel in order to avoid finishing grinding. This research considers the turning of hardened steel without cooling with two types of tools: cubic boron nitride (CBN) and hard metal (HM) inserts. To estimate the influence of machining conditions on cutting temperature, a central composition design with three factors on five levels was used. The development of advanced models allows one to meet the accelerated demands in terms of productivity, product quality, and reduced production costs. Based on experimental data, three input regimes (cutting speed, feed, and depth of cut), and one attributive factor (tool material) were used as input variables, while cutting temperature was used as the output of the adaptive neuro-fuzzy inference systems (ANFIS). The model was trained, tested, and validated with a combined input/output data set. The obtained ANFIS model could be applied with high precision to determine the cutting temperature in machining of hardened steel. From an economic point of view, the obtained model can directly affect the cost of processing because cutting temperature and tool life are directly relieved.

1. Introduction

Due to the technical and economic significance of cutting technology, numerous studies have been carried out, all of which were in order to model the process itself to increase machining quality and productivity, and thus reduce processing costs [1]. According to Armarego [2], in the United States, the correct choice of tools is made in less than 50% of cases, while the nominal cutting speed is used in 58% of cases, and 38% of the tool is used up to its maximum durability.

The main objectives of process modelling treatment are to increase the productivity, efficiency, total quality of products or individual aspects (machined surface, tool life, etc.) and reducing the consumption of materials, energy, processing time, and processing costs per unit of product [3]. It is difficult to theoretically use analytical models reliably to determine the processing parameters such as tool wear, optimum geometric shape, deformation phenomena in the tool, limit deformation, tribological processes, and tool loads, because in each machining process, there are several influential factors with interactions between them.

It is well known that during hard machining, because of the great influence on the final characteristics of machining parts, cutting temperature is of significance. Cutting temperature is also very important from the economic side and optimization of the machining process [4]. In the manufacturing industry, there is an increased demand for high quality products, high productivity, and overall economy by hard machining, especially in meeting global cost competitiveness. Therefore, it is of great importance to make an initial model that will be able to determine and evaluate the cutting temperature as one of the main output characteristics in hard machining.

In the machining processes, the significance of cutting temperature has been well accepted in the metal processing industry from two points of view. The first reflects on the impact on tool wear and on the processing efficiency limit. The second relates to the important effect on the integrity of the workpiece surface, i.e., the heat affected zone, in terms of hardness and surface roughness [5,6]. In Mia and Dhar [7], it is shown that the prediction of the cutting temperature plays an essential role in the machining industry for the correct planning and control of processing parameters and optimizing cutting conditions.

For specific and demanding machining operations, the ability to obtain new information is a very important advantage [8,9]. One of the most common indicators of tool wear is cutting temperature [10]. These findings have been confirmed by many researchers, among them Ay and Yang [11]. They monitored the cutting temperature using an infrared camera and evaluated the influence of heat expansion to the cutting tool. Based on this, the authors explained that increasing the temperature of the tool accelerates the process of tool wear. This statement is of great importance because the costs of cutting tools and their replacement must be reduced to a minimum [12,13]. From an economic point of view, the tool wear has a main role in machining processes. Also, Jawahir et al. [14] are convinced that the identification of optimal processing parameters is essential for economical processing.

Many researchers who participated in the modelling of cutting temperature used different techniques. One of the possibilities is the application of an artificial intelligence tool, which proved to be very successful in the modelling of machining processes [15,16]. Intelligent modelling techniques have good properties for modelling complex manufacturing processes [17,18]. In recent years, a large range of artificial intelligence (AI)-based techniques have been developed that model the correlation between the input (process data such as cutting speed, feed, and depth of cut) and the output (tool life, cutting temperature, surface quality, etc.) parameters of the turning process. Mia et al. have considered the optimization of hard-turning parameters using evolutionary algorithms [19]. In their work, the investigated machining parameters were cutting speed, feed rate, and depth-of-cut, while the output parameters were surface roughness and cutting temperature. An example of a cutting temperature prediction for the turning of biomedical stainless steel is carried out by Petkovic et al. [20]. These authors used a neural network with an optimization algorithm for the quick, easy, and successful optimization of input regimes. Consequently, an intelligent model on the basis of a neural network is a good feature for generalization and has the ability to accept non-linear variables with unknown iterations. Mikołajczyk et al. predicted tool life in turning operations using neural networks [21]. Their results confirm that the combination image recognition software and ANN (Artificial neural networks) modeling could potentially grow into a useful industrial tool for cheap estimation of tool life in agile operations. One example of the application of fuzzy logic is shown by Prabhu et al. [22]. They used a fuzzy logic analysis method to predict the optimal solution, and to find out the most influential parameter to determine the output characteristics. Also, the use of artificial intelligence tools, such as an adaptive neural fuzzy inference system (ANFIS), enables a positive development of the manufacturing industry [23]. ANFIS is one of the most powerful techniques used for modelling, and is based on a fuzzy inference system and neural network, which are used to model complex relationships in various branches of industry and engineering that are difficult or impossible to explain to classical models [24]. In addition to prediction and optimization, which give a fuzzy logic, neural networks, and evolutionary algorithms, the ANFIS technique provides the ability to recognize the significance of input parameters. This intelligence technique has been successfully used in modelling various machining processes, such as turning, milling, and drilling [25,26,27]. According to literary sources, in predicting the output characteristics of the cutting process, ANFIS models have proven to be very efficient.

Machining of hard materials by turning has been receiving special attention because it offers many possible benefits over grinding in machining hardened steel [28,29]. Research shows that it is possible to perform machining on the turn while achieving a high accuracy and small roughness of the treated surface, in contrast with the more expensive grinding, which allows for significant technical and economic effects, the most important of which are:

• Reducing the processing time and costs (in relation to finishing grinding).
• It is feasible to handle multiple surfaces in one clamp, which is rarely possible when grinding, avoiding the effects that occur during grinding (the appearance of structural changes due to overheating of the surface layer, residual stresses, and cracks), and improving the exploitation characteristics of the parts.

The use of cubic boron nitride (CBN) tools for rigid turning for rough- and semi-finishing is recognized as a technologically and economically flexible process. Because of the poor thermal conductivity of CBN, the heat generated during the cutting process is taken with a part separated from the cutting zone, eliminating the use of coolants and lubricants. In addition, the dry surface finish is most effective in the realization of the process due to more stringent regulations on the protection of the environment and increasing the costs associated with disposing substances used for cooling and lubrication. The use of coolants/lubricants during cutting is widely accepted as a temperature control for improving the quality of the system and surface. However, the practice of using coolants/lubricants is expensive and causes serious damage to the environment and human health [19]. Processing of hard materials requires the use of special and expensive tools. The inserts of cubic boron nitride are the most often used inserts in processing hardened steels. The main feature of these inserts is resistance to temperature, which directly affects the economy of processing. It is known that in the turning process, variations of the input parameters, such as cutting speed, feed, and depth of cut, affect the cutting temperature in the same way on the wear of the tool [30].

In view of all the above, it is necessary to determine an economical method of temperature measurement at which it can be directly controlled and allows one to determine the state of tool wear [31]. There are many ways to measure the cutting temperature, namely using a thermograph, thermocouple, thermistor, pyrometer, etc. In the field machining, a thermographic determination of cutting temperature is often found. An example of this measurement is shown by Muller et a1. [32]. The authors determined the distribution of temperature on the surface of tools with a diamond coat. They used the thermographic principle to determine the dependence between input processing parameters and temperature distribution in the processing zone.

Because of all this, this research deals with the application of an ANFIS intelligent technique for modelling the process of difficult-to-cut alloy EN 90MnCrV8 in order to determine the relationship between the input parameters and cutting temperature. The advantage of this paper is reflected in the application of the turning process for hard materials that gives better productivity and satisfactory quality. The cutting temperature is a relevant factor in the turning process, which is influenced by the machining parameters. It refers to tool geometry, like nose radius, edge geometry, rake angle, chamfer thickness, etc.; machining conditions (depth of cut, cutting speed, feed, etc.); and properties of the workpiece. Due to the poor application of ANFIS tools in hard steel turning, the contribution to the work is not only reflected in the application of this technique, but it also presents a comparison of two tool materials, with zero rake angle, namely cubic boron nitride and hard metal. Comparative analysis has shown that CBN generates a lower cutting temperature than HM.

This research covers the modelling of the cutting temperature in the turning of hard steel using the ANFIS technique. The most important processing parameters were selected, namely cutting speed, feed, depth of cut, and an attribute factor related to the tool material. The ANFIS model has the ability to predict cutting temperature for both materials, which gives a relationship between the input and output data in order to improve machining operations.

2. Experimental Setup

Due to the many expensive experiments carried out, in this research, turning operations were performed without lubrication and cooling agents. During the turning of the hard steel to determine the influence of the tools on the cutting temperature, the three-factor plan of the experiment was used at five levels (

Table 1. Turning conditions.

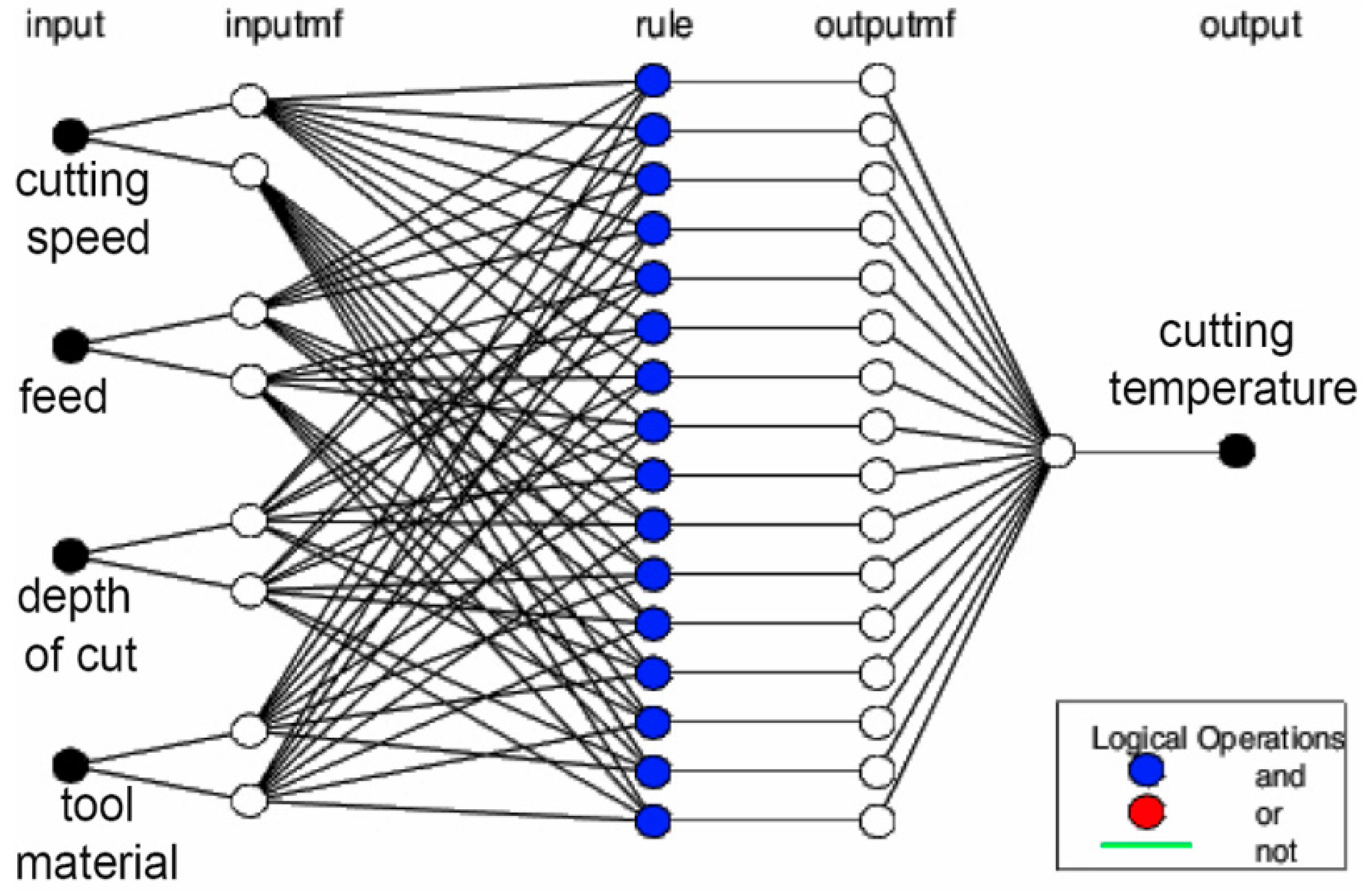
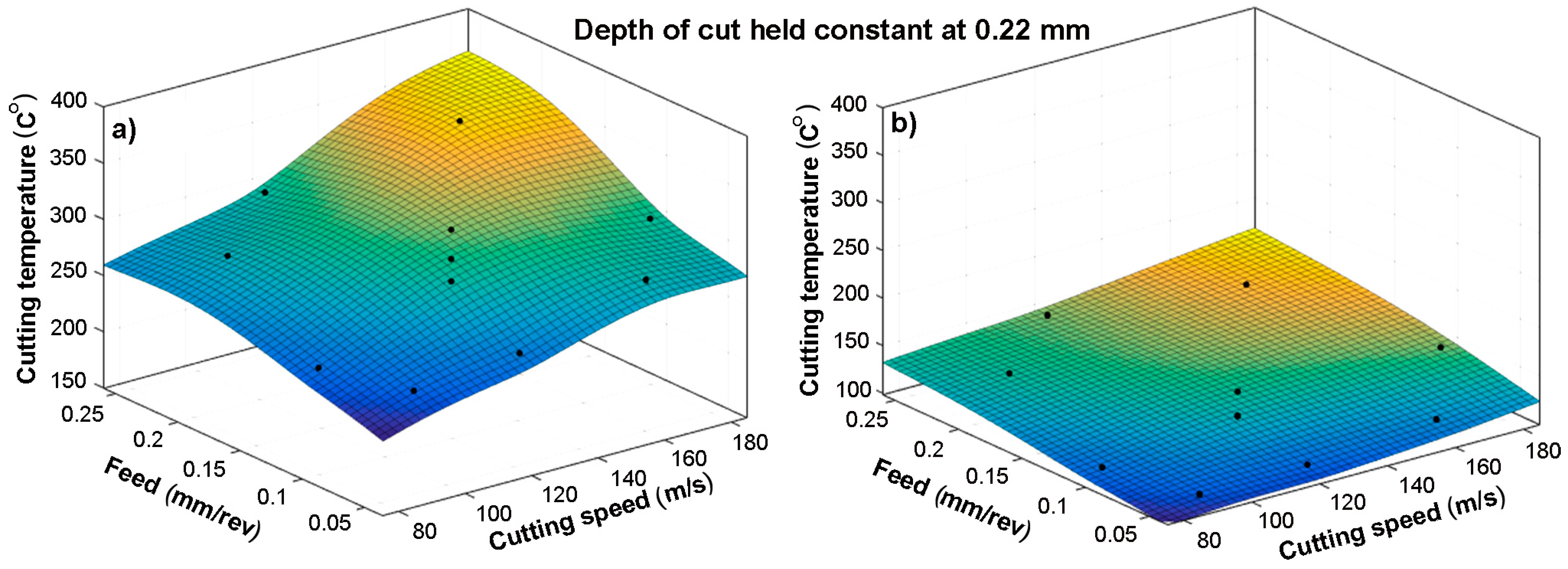
Machining Parameters	Level 1	Level 2	Level 3	Level 4	Level 5
Cutting speed vc (m/min)	80	90	120	160	180
Feed f (mm/rev)	0.045	0.05	0.1	0.2	0.25
Depth of cut a (mm)	0.07	0.1	0.22	0.5	0.7

). To determine the difference between the tool materials, two inserts were selected for experiments, cubic boron nitride and hard metal.

As one of the hard-working materials, EN 90MnCrV8 is known as a cold working steel. This material has a hard-wearing hardness of 55 HRC. Steel is thermally treated in such a way to ensure the mentioned hardness in the machining zone of each workpiece. The chemical composition of the selected material is shown in

Table 2. Chemical composition of EN 90MnCrV8.

C (%)	Si (%)	Mn (%)	Cr (%)	V (%)
0.9	0.25	2	0.35	0.1

.

Specifications of the tool insert are presented in

Table 3. Specifications of inserts that were used as tool material.

Inserts		Rake Angle	Back Angle	Inclination Angle	Tool Cutting Edge Angles		Nose Radius	Side Clearance
		γ (°)	α (°)	λ (°)	κ (°)	κ1 (°)	r (mm)	(°)
CBN	CNMA 120404	−6	6	−6	91	5	0.4	0
HM	CNMA 120404	−6	6	−6	91	5	0.4	0

. The same experimental plan was carried out for both the tool materials, as shown in

Table 4. The measurement and modelled RSM results—input parameters.

No.	Factor			…Θi Measured		Θi Model
	v (m/min)	f (mm/rev)	a (mm)	HM Θ (°C)	CBN Θ (°C)	HM Θ (°C)	CBN Θ (°C)
1.	90	0.05	0.10	230	104	232.08	102.65
2.	160	0.05	0.10	280	119	275.56	119.65
3.	90	0.20	0.10	268	121	267.65	127.43
4.	160	0.20	0.10	350	169	317.79	148.53
5.	90	0.05	0.50	242	108	246.30	110.49
6.	160	0.05	0.50	285	118	292.44	128.78
7.	90	0.20	0.50	286	143	284.05	137.16
8.	160	0.20	0.50	350	138	337.26	159.87
9.	120	0.10	0.22	277	121	279.60	128.01
10.	120	0.10	0.22	283	130	279.60	128.01
11.	120	0.10	0.22	264	131	279.60	128.01
12.	120	0.10	0.22	266	120	279.60	128.01
13.	80	0.10	0.22	245	105	247.74	114.91
14.	180	0.10	0.22	298	137	315.57	142.61
15.	120	0.045	0.22	254	113	257.56	113.02
16.	120	0.25	0.22	293	139	307.24	147.67
17.	120	0.10	0.07	290	130	268.02	121.48
18.	120	0.10	0.70	310	156	291.82	134.97
19.	80	0.10	0.22	240	115	247.74	114.91
20.	180	0.10	0.22	290	145	315.57	142.61
21.	120	0.045	0.22	250	102	257.56	113.02
22.	120	0.25	0.22	286	145	307.24	147.67
23.	120	0.10	0.07	282	130	268.02	121.48
24.	120	0.10	0.70	336	104	291.82	134.97

.

According to the experiment plan, testing was carried out by turning on a round workpiece. By way of preparation, workpieces with a diameter of 34 mm and a length of 500 mm were machined on the conventional lathe with a power of 10 kW. During the experiment with two types of tools, namely CBN and HM, the cutting temperatures were monitored. For the purpose of measuring the cutting temperature, a FLIR E50 (FLIR systems, Wilsonville, Oregon, US) thermal camera was used. In order to ensure the measurement of accurate cutting temperatures, the thermal camera was fixed on a tool holder (Figure 1).

The thermal camera was moved in the same area at the same time with the tool. The 0.95 parameters as the emission factor were adopted as the highest chip temperature. In the selected area, the thermal camera simultaneously measured the minimum, maximum, and average temperature. During the entire machining process, the cutting temperature was monitored, while the calculation was executed every 5 s.

3. Response Surface Methodology

The measured values of cutting temperature and determined values using three factorial models are given in Table 4. Using the surface response methodology, Equations (1) and (2) were obtained, which determine the cutting temperature for each individual tool material.

$$\mathrm{For}\mathrm{HM}\mathrm{tool}:\Theta =89.7785\cdot v^{0.29845}\cdot f^{0.10286}\cdot a^{0.03694}$$

(1)

$$\mathrm{For}\mathrm{CBN}\mathrm{tool}:\Theta =54.8983\cdot v^{0.26632}\cdot f^{0.15597}\cdot a^{0.04572}$$

(2)

4. Adaptive Neuro-Fuzzy System

The MATLAB 16 (MathWorks, US) software was used to identify the adaptive neuro-fuzzy inference “system-ANFIS” model. This is one of the most commonly used programs for creating intelligent models [18]. To train and create an ANFIS, the fuzzy logic toolbox in the program MATLAB was used. The ANFIS architecture is based on the Sugeno type of fuzzy inference system [19]. This method represents an effective system for undertaking complex tasks where knowledge is expressed through the if–then rules. With the help of the neural network and fuzzy logic, ANFIS suggests a relationship of mapping between input and output data. For the optimal adjustment of membership functions, the most useful hybrid learning method is used [20]. The ANFIS model structure is based on fuzzy logic, while the neural network is only used in model training [21].

Figure 2 shows the basic architecture of the ANFIS model. In this case, a five-layer neural network was used that simulated the operation of a fuzzy inference system (Figure 2). Every layer of the network has its role here.

Figure 3 shows a five-layer neural network through which the ANFIS model training was performed. Input values (crisp signal), such as cutting speed, feed, depth of cut, and tool material, were converted to fuzzy values through the membership functions. The key roles when creating the ANFIS model are the membership function and the rule base. Based on experimental data, a set of rules was generated by defining the number and type of membership functions.

The structure of the neuro-fuzzy model consisted of five different adaptive layers. Below is a brief description of the Sugeno first-order model with two input variable variables.

Layer 1: The fuzzification layer, where the names of the fuzzy sets or language variables are defined.

$$\begin{array}{l}{O}_i^1={\mu }_{Ai}\left(x_2\right),i=1,2\\ O_j^1={\mu }_{Bi}\left(x_2\right),i=1,2\end{array}$$

(3)

where $O_{iorj}^1$ are output functions and ${\mu }_{AiorBi}$ are membership functions.

Layer 2: Represents the result of layer 1. Here the weight functions $w_i$ for the next layer is defined.

$$O_i^2=w_i={\mu }_{Ai}\left(x_1\right){\mu }_{Bi}\left(x_2\right),i=1,2$$

(4)

Layer 3: In this layer, the normalization of the value from layer 2 is carried out and is transferred to layer 4.

$$O_i^3={\overline{w}}_i=\frac{w_i}{{\Sigma }_i{w}_i}i=1,2$$

(5)

Layer 4: The de-fuzzification layer. In this layer, the linear parameters p_i, q_i, and r_i that result from the function are defined.

$$O_i^4={\overline{w}}_i\cdot f_i={\overline{w}}_i\left(p_i\cdot x_1+q_i\cdot x_2+r_i\right)i=1,2$$

(6)

Layer 5: The total output layer. The total number of output signals is the output from this layer.

$$Q_i^5=f\left(x_1,x_2\right)=\underset{i}{\Sigma }{\overline{w}}_i\cdot f_i={\overline{w}}_i\cdot f_1+{\overline{w}}_i\cdot f_2=\frac{{\Sigma }_i{w}_i\cdot f_i}{{\Sigma }_i{w}_i}.$$

(7)

The most significant steps in identifying the ANFIS model are the training and testing steps that defined the model’s characteristics. The total number of experimental data used to generate the ANFIS model was 48. Approximately 70% of the data was used to successfully train the model, while the remaining 30% is used for testing. Therefore, for this study, 36 training data points and 12 test data points were used.

There are more possible membership functions, but for this research, the Gaussian function was chosen. From the crisp input, the neural network passes data using the membership functions. Neural networks define the basic rules that are associated with system locking. The hybrid learning method was used to train the adaptive network and the proper form of the membership function. The training was conducted with 500 epochs. During the model training, new rules and forms of membership functions were constantly generated to get the output with the smallest error. When the model’s error was acceptable, the model was tested. The model was accepted when the relative errors of training and testing were below 10%.

5. Results

The hard-turning operation with both tool materials were controlled by three factors, namely the cutting speed, feed rate, and depth of cut. Therefore, these parameters generally affected the possible results of the machining. For that reason, the mean behaviors of the cutting temperature were evaluated using dispersion analysis and a main effect plot. The main effect plot shows a relative change from the center point of the experiment.

After the dispersion analysis, the adequacy of the model (Fa) and the significance of the input parameters (Fr₀, Fr₁, Fr₂ and Fr₃) were determined and are presented in

Table 5. Adequacy of models and significance of parameters.

Model Adequacy		HM Θ (°C)	CBN Θ (°C)
		Fa = 4.20467	Fa = 3.77465
Significance	Fro	679937.42	214918.52
	Fr1 (v)	105.27	71.11
	Fr2 (f)	72.60	35.71
	Fr3 (a)	12.62	8.24

. Based on this analysis and the obtained statistical parameters, it can be concluded that the obtained values for the adequacy of the empirical models and the significance of the input parameters were sufficiently reliable.

It is evident from Figure 4a that the increase in cutting speed caused an increase in the cutting temperature. The reason for the increase in cutting temperature was due to the conversion of mechanical energy (rotation of spindle) into heat energy. The cutting speed with the CBN tool had a similar effect (Figure 4b). The effects of the feed on the cutting temperature for both tool material were contrary to expectations.

For instance, an increase in feed rate caused a significant increase in cutting temperature. Lastly, depth of cut also effected the cutting temperature, especially when turning with an HM tool, while with CBN, it showed a smaller effect. This can be explained by the fact that the tool material of cubic boron nitride has better thermal conductivity. This was also confirmed by experiments that showed that generally higher temperatures occur with HM tools [12]. The maximum temperature for HM was 350 °C, while for CBN, it was 169 °C.

Compared to literature sources, the cutting temperatures obtained in this paper were lower. This happened by adopting a medium cutting speed according to the manufacturer’s recommendations as a way to measure temperature. The use of thermocouples gave a more realistic temperature, but on the economic side, it is quite expensive.

It is also appreciable for HM tool that all three input parameters had a significant effect on cutting temperature. Compared to these machining parameters, the depth of cut played a small role in defining cutting temperature values, especially with CBN tools. Hence, during optimization, the change in cutting speed, feed, and depth of cut were most significant to favorably align the value of the responses, while for CBN tools, one should pay attention to only the cutting speed and feed.

The main contribution of this paper is the application of ANFIS intelligent techniques in modelling cutting temperature. The model results obtained for the cutting temperature are shown in

Table 6. Experimental plan and results.

Input of ANFIS					Temperature Θ (°C)
Tool Material		vc (m/min)	f (mm/rev)	a (mm)	Experimental		ANFIS
CBN	HM				CBN	HM	CBN	HM
Training data
1.	19.	90	0.05	0.1	104	165	103.9	164.6
2.	20.	160	0.05	0.1	119	122	119.0	121.9
3.	21.	90	0.2	0.1	121	150	121.0	149.9
4.	22.	160	0.2	0.1	169	200	169.0	200.0
5.	23.	90	0.05	0.5	108	230	108.0	229.9
6.	24.	160	0.05	0.5	118	189	118.0	188.2
7.	25.	90	0.2	0.5	143	245	143.0	244.9
8.	26.	160	0.2	0.5	138	230	137.9	230.0
9.	27.	120	0.1	0.22	121	280	127.3	280.0
10.	28.	120	0.1	0.22	130	183	127.3	188.2
11.	29.	120	0.1	0.22	131	184	127.3	188.2
12.	30.	120	0.1	0.22	120	190	127.3	188.2
13.	31.	80	0.1	0.22	105	196	97.0	183.3
14.	32.	180	0.1	0.22	137	200	140.9	201.0
15.	33.	120	0.045	0.22	113	210	113.0	208.9
16.	34.	120	0.25	0.22	139	160	139.0	164.6
17.	35	120	0.1	0.07	130	208	129.9	183.9
18.	36.	120	0.1	0.7	156	161	130.23	161.0
Average error for training data: 2.1%
Test data
37.	41.	80	0.1	0.22	115	202	97.0	201.0
38.	42.	180	0.1	0.22	145	195	140.9	183.3
39.	43.	120	0.045	0.22	102	165	113.0	164.6
40.	44.	120	0.25	0.22	145	210	139.0	208.9
Average error for test data: 5.1%
Validation data
45.	47.	120	0.25	0.22	145	160	139.3	165.6
46.	48.	120	0.1	0.07	130	250	127.2	229.4
Average error for validation data: 4.5%

. In order to verify the reliability of the adopted ANFIS model, a calculation of absolute relative errors between experimental and model data was performed. The absolute relative error was calculated for the training, testing, and validation data. All errors were within the allowed limits, i.e., less than 10%, and the adopted model can be used with a high reliability for the analysis and prediction of cutting temperature, as well as the optimization of input parameters.

Another ANFIS model for reliability confirmation is shown using the correlation diagrams. The diagrams in Figure 5 show correlations between the experimental and model values. It can be seen that the lines approximate to each other, confirming the good agreement of results.

The resulting ANFIS model has the ability to display three-dimensional surfaces. From the 3D diagrams shown in Figure 6, the influence of individual processing parameters can be determined, such as cutting speed, cutting position, and cutting depth, in relation to cutting temperature. According to the dispersion analysis, the depth of cut had the least influence; therefore, it was maintained at a constant value and only the influence of the cutting speed and feed are displayed on the 3D diagrams. Diagrams are shown for a center point with a depth of cut of 0.22 mm. Also, from these diagrams, the optimum processing parameters can be determined to obtain the minimum cutting temperature for both tool materials. The minimum limit temperature for both tool materials could be achieved when the cutting speed and feed were maintained at minimum values.

The above analysis indicates that among the three turning machining parameters and one attributive factor discussed in this study, i.e., cutting speed, feed, depth of cut, and tool material, the cutting speed and feed had the most substantial effect on cutting temperature, followed by the depth of cut. The analysis of the influence of input processing parameters was confirmed using dispersion analysis of empirical models, main effect plots, and 3D surfaces of the ANFIS model.

6. Conclusions

This paper introduces an adaptive neuro-fuzzy system that allows for the analysis and predicting of cutting temperature, as well as the optimization of input processing parameters. The ANFIS model was developed based on a three-factor experimental plan. The plan was developed for testing the machining by turning EN 90MnCrV8. Dispersion analysis is an indication that high empirical models have been obtained. Based on this analysis and main effect plot, it was determined that cutting speed and feed has the greatest influence on temperature of all three input parameters. The slightly smaller impact with both tool materials was shown by the depth of cut, especially with the CBN tools. It was also deduced that a higher cutting temperature was observed when processing with the tool made from hard material. By comparing the ANFIS model with experimental data, it can be noticed that the ANFIS model is very reliable. The absolute relative error of the ANFIS model was within the permissible limits. From all of this, it can be concluded that adaptive neuro-fuzzy modelling technique is an economical and highly successful method for predicting one of the processing output variables, which was the cutting temperature in this case. The obtained model can be significantly improved with the expansion of input parameters and distribution, as well as new tool materials.